2 1 TCNICAS DE CONTEO Cuando los diversos

2. 1 TÉCNICAS DE CONTEO Cuando los diversos resultados de un experimento son igualmente probables (la misma probabilidad es asignada a cada evento simple), la tarea de calcular probabilidades se reduce a contar. Sea N el número de resultados en un espacio muestral y N(A) el número de resultados contenidos en un evento A.

Si una lista de resultados es fácil de obtener y N es pequeño, entonces N y N(A) pueden ser determinadas sin utilizar ningún principio de conteo. Existen, sin embargo, muchos experimentos en los cuales el esfuerzo implicado al elaborar la lista es prohibitivo porque N es bastante grande. Explotando algunas reglas de conteo generales, es posible calcular probabilidades sin una lista de resultados.

� Por ejemplo: Es muy sencillo la solución a este problema: imagínate que tu jefe te pide que cuentes los últimos productos que han llegado en la última hora. En este caso podrías ir y contar uno a uno los productos.

2. 1. 1 PRINCIPIO ADITIVO � Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas. . . y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo. �M + N +. . + W maneras o formas

�Ejemplo: � 1) Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?

� Solución: � � � M = Número de maneras de seleccionar una lavadora Whirpool N = Número de maneras de seleccionar una lavadora de la marca Easy W = Número de maneras de seleccionar una lavadora de la marca General Electric M = 2 x 4 x 2 = 16 maneras N = 3 x 2 = 12 maneras W = 1 x 2 x 1 = 2 maneras � � M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora

� 2) Un estudiante que está terminando su bachillerato, debe decidir si estudia en el Tecnológico o en la Universidad. Si decide estudiar en el Tecnológico, tendrá que decidir si estudia Ing en Sistemas Computacionales, Ing Mecánica o Ing Electrónica. Si decide estudiar en la Universidad, tendrá que decidir si estudia Ing Civil, Ing Mecatrónica, Ing Química o Licenciado en Física. ¿Cuántas opciones tiene para elegir su carrera?

� Solución: Si decide estudiar en el Tecnológico, tendrá 3 opciones, pero si decide estudiar en la Universidad, tendrá 4 opciones. � Aplicando el Principio Aditivo, obtenemos 3 + 4 = 7 opciones, considerando que no puede estudiar 2 carreras al mismo tiempo.

� ¿Cómo podemos distinguir cuando hacer uso del principio multiplicativo y cuando del aditivo? � Es muy simple, cuando se trata de una sola actividad, la cual requiere para ser llevada a efecto de una serie de pasos, entonces haremos uso del principio multiplicativo y si la actividad a desarrollar o a ser efectuada tiene alternativas para ser llevada a cabo, haremos uso del principio aditivo.

2. 1. 2 PRINCIPIO MULTIPLICATIVO � Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es: P(A y B) = P(A)P(B) si A y B

� Son independientes � P(A y B) = P(A)P(B|A) si A y B � Son dependientes � P(A y B) = P(A B) = P(B)P(A|B) si A y B

Son dependientes � Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N 1 maneras o formas, el segundo paso de N 2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de; � � � N 1 x N 2 x. . x N r maneras o formas El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.

� Ejemplo: � 1)Una persona desea construir su casa, para lo cual considera que puede construir los cimientos de su casa de cualquiera de dos maneras (concreto o block de cemento), mientras que las paredes las puede hacer de adobe, adobón o ladrillo, el techo puede ser de concreto o lámina galvanizada y por último los acabados los puede realizar de una sola manera ¿cuántas maneras tiene esta persona de construir su casa?

� Solución: � Considerando que r = 4 pasos � N 1= de de maneras � N 2= maneras � N 3= maneras � N 4= maneras � N 1 x hacer cimientos = 2 construir paredes = 3 hacer techos = 2 hacer acabados = 1 N 2 x N 3 x N 4= 2 x 3 x 2 x 1 = 12 maneras de construir la casa

� Para abreviar estas expresiones, se usa una notación especial llamada notación factorial y nos denota las multiplicaciones sucesivas de n hasta 1 y se define como: 4 x 3 x 2 x 1 = 4! Se lee cuatro factorial � 3 x 2 x 1 = 3! Se lee tres factorial � En términos generales: (n-1)(n-2) «x 2 x 1 = n! Se lee “n factorial” � Ejemplo 1 � Hallar 6! � Solución: 6!=1 x 2 x 3 x 4 x 5 x 6 =720, � Así, 6!=720. �

2. 1. 3 NOTACION FACTORIAL � Se usa la notación n! para denotar el producto de los enteros positivos desde 1 hasta n. � 1) N! 1 x 2 x 3 x………………… x n � 2) 0! =1 � 3) 1!=1 � 4) N!=(n-1)! x n � Notación factorial: es el producto de n entero positivo hasta 1. � n! =n (n-1)*(n-2)*(n-3)* «. *3*2*1 � En algunos problemas de matemáticas se nos presentan multiplicaciones de números naturales sucesivos tal como: 4 x 3 x 2 x 1 = 24; 3 x 2 x 1 = 6; 2 x 1 = 2.

� Ejemplo 2 � Descomponer 10! � Solución: 10! = 10 x 9! o también puede ser � 10! = 10 x 9 x 8! o también � 10! = 10 x 9 x 8 x 7! y así sucesivamente. �

2. 1. 4 PERMUTACIONES � Sin embargo, cuando se tienen grandes cantidades se utilizará el término de factorial y la fórmula se expresará de la siguiente manera:

Ejemplo: � En un estudio de mercado se realiza un cuestionario para determinar las preferencias del consumidor de cierto refresco de marca. El encuestado debe seleccionar de seis rubros, cuatro razones por las que le interesa consumir el refresco, además que debe ordenar de mayor a menor, anotando con el número 1 el de mayor interés y con el 4 el de menor interés. � ¿De cuántas maneras puede responder un ciudadano el cuestionario?

� Solución: � como un encuestado debe ordenar cuatro de los seis problemas, y es importante el orden que da, la respuesta es el ordenado de seis elementos tomando únicamente cuatro, por tanto es una permutación n= 6, ya que éste es el número total de opciones que se pueden contestar en el cuestionario y r= 4 opciones que se eligen, donde es importante el orden que se le da a cada una.

2. 1. 5 COMBINACIONES � La combinación se da sin importar el orden de r objetos sin repetición, seleccionados de entre n objetos tomado de r en r; las combinaciones se anotan con la nomenclatura n. Cr. Por tanto, el número de combinaciones de n objetos tomados de r en r está dado por:

� Ejemplo: En el departamento de una empresa hay 20 trabajadores, quienes deben cubrir una guardia el fin de semana por lo que se formará un grupo de guardia el día sábado conformado por cuatro trabajadores. ¿Cuántos grupos diferentes de 4 miembros son posibles?

� Solución: En este ejemplo, el orden de los miembros que conforma el grupo de guardia no es importante, ya que no es necesario determinar cómo van a estar acomodados los integrantes del grupo, por lo tanto:

2. 1. 6 DIAGRAMA DE ÁRBOL � Un diagrama de árbol puede construirse en varios pasos o etapas, entonces cada una de las maneras de completar el primer paso puede representarse como una rama del árbol. Cada una de las maneras de completar el segundo paso puede representarse con el numero de ramas que comienzan donde terminan las ramas originales y así sucesivamente dependiendo de que tan grande sea el espacio muestral.

� por ejemplo: En un sistema de comunicación digital cada mensaje se clasifica según llega o no dentro del tiempo establecido por el diseño del sistema. Si se clasifican tres mensajes, utilice un diagrama de árbol para denotarlo y representar los resultados.

Entonces se dice que tenemos 8 posibles combinaciones multiplicando nuestras ramas tenemos 2 x 2 x 2=8 entonces tenemos 8 posibles combinaciones diferentes.

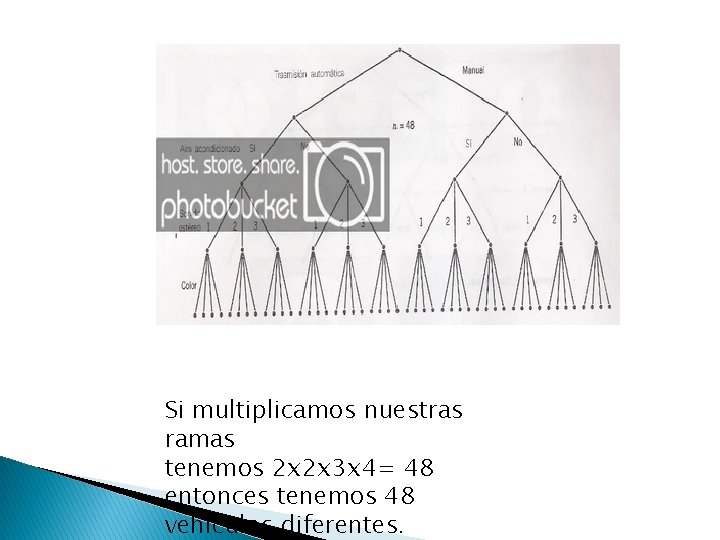
� Ahora veamos uno mas complejo: El fabricante de un automóvil proporciona vehículos equipados con distintas opciones que el cliente selecciona. Cada vehículo se solicita Con o sin transmisión automática Con o sin aire acondicionado Con una de tres opciones posibles en cuanto a un sistema de sonido estéreo Con uno de cuatro colores exteriores nuestro diagrama de árbol queda así:

Si multiplicamos nuestras ramas tenemos 2 x 2 x 3 x 4= 48 entonces tenemos 48 vehículos diferentes.

2. 1. 7 TEOREMA DEL BINOMIO � El teorema del binomio, también llamado binomio de Newton, expresa la enésima potencia de un binomio como un polinomio. El desarrollo del binomio ( a + b)^n posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en otras áreas del conocimiento.

� Formula General Del Binomio. Sea un binomio de la forma (a + b). Si a este binomio se le multiplica sucesivamente por sí mismo se obtienen las siguientes potencias:

� Ejemplo:

2. 2 TEORIA ELEMENTAL DE PROBABILIDAD � El Cálculo de Probabilidades se ocupa de estudiar ciertos experimentos que se denominan aleatorios, cuya característica fundamental es la incertidumbre del resultado, esto significa que es imposible predecir los resultados porque hay más de uno posible.

� Son ejemplos de experimentos aleatorios: lanzar un dado cinco veces, los instantes de llegadas a un abarrote, etc. � El término de probabilidad es de uso común, así el ente televisivo, el cual nos dirá que es poco probable un cambio brusco de temperatura ó un periódico informará que es muy probable que el Real Madrid gane en su campo a Las Palmas.

Concepto Clásico De Probabilidad* � También conocido como probabilidad a priori. “Si para un evento A hay n resultados igualmente probables, de las cuales f son del tipo que nos interesa, la probabilidad de que ocurra un resultado de este tipo es: P(a)=f / n

2. 3 Probabilidad de eventos : Definición de espacio muestral , definición de eventos, simbología , unión, intersección, diagramas de Venn. � Definición de espacio muestral: � � El concepto de espacio se refiere al área que consigue contener a la materia existente, la capacidad de un territorio o la porción que ocupa un objeto sensible. � � Muestral, por su parte, es lo que pertenece o guarda relación con una muestra (tal como se conoce a la parte que se extrae de un conjunto mediante algún método que permite considerarla como representativa de éste). Una muestra también es una evidencia, demostración, prueba o señal de algo.

� Por espacio muestral (también conocido como espacio de muestreo) se entiende el grupo de todos los resultados específicos que se pueden obtener tras una experimentación de carácter aleatorio. A cada uno de sus componentes se les define como puntos muéstrales o, simplemente, muestras. � EJEMPLO: si la prueba se basa en arrojar un dado, el espacio muestral estará constituido por los puntos muéstrales identificados como los números 1, 2, 3, 4, 5 y 6, ya que esos son los resultados posibles de la acción de tirar el dado. Por lo tanto, se puede establecer que el espacio muestral del experimento es U = {1, 2, 3, 4, 5, 6}

� Los espacios muéstrales pueden clasificarse como discretos (cuando la cantidad de sucesos elementales es finito o numerable) o continuos (en los casos en los cuales la cantidad de sucesos básicos posee carácter infinito y, por lo tanto, resulta imposible de contar).

Definición de evento: � Un evento es un resultado particular de un experimento aleatorio. En términos de conjuntos, un evento es un subconjunto del espacio muestral. Por lo general se le representa por las primeras letras del alfabeto.

Ejemplo: � A: Que salga un número par al lanzar un dado. � E: Que haya que esperar más de 10 minutos para ser atendidos. � � Evento Nulo: � Es aquel que no tiene elementos. Se representa por φ. � � Evento Seguro: � Es el espacio muestral que puede ser considerado como un evento. � �

Evento: � La probabilidad clásica de un evento E, que denotaremos por P(E), se define como el número de eventos elementales que componen al evento E, entre el número de eventos elementales que componen el espacio muestral:

� Cuando se tiene un espacio muestral llamamos, formalmente evento o suceso a cualquier subconjunto del espacio muestral. � Decimos que un suceso se realiza, cuando el resultado del experimento aleatorio es uno de los sucesos posibles. � Se llama evento o suceso a todo subconjunto de un espacio muestral. Por ejemplo en el espacio muestral E = {1, 2, 3, 4, 5, 6} del lanzamiento de un dado, los siguientes eventos: � Obtener un número primo, A = {2, 3, 5} � Obtener un número primo y par, B = {2} � Obtener un numero mayo o igual a 5, C = {5, 6}

Simbología, Unión e Intersección � � � � A, B, C… = conjuntos. a , b , c… = elementos de conjuntos. U = unión de conjuntos. ∩ = intersección de conjuntos. A‟ = complemento de un conjunto. / = dado que = diferencia <> = diferente de ( ) = conjunto nulo o vacío R = conjunto de los números reales N = conjunto de los números naturales C = conjunto de los números complejos n! = factorial de un numero entero positivo Q = conjunto de los números fraccionarios I = conjunto de los números irracionales c = subconjuntos { } = llaves.

� � Conjuntos vacíos Si A y B son dos subconjuntos de un conjunto S, los elementos que pertenecen a A, a B o a ambos forman otro subconjunto de S llamado unión de A y B, escrito A U B. Los elementos comunes a A y B forman un subconjunto de S denominado intersección de A y B, escrito A& cap. B. Si A y B no tienen ningún elemento común se denominan conjuntos disjuntos ya que su intersección no tiene ningún elemento, y siendo conveniente representar esta intersección como otro conjunto, éste se denomina conjunto vacío o nulo y se representa con el símbolo Ø. Por ejemplo, si A = {2, 4, 6}, B = {4, 6, 8, 10} y C = {10, 14, 16, 26}, entonces A U B = {2, 4, 6, 8, 10}, A U C = {2, 4, 6, 10, 14, 16, 26}, A ∩ B = {4, 6} y A ∩ C = Ø.

Diagramas de Venn: � Los diagramas de Venn son ilustraciones usadas en la rama de la Matemática y Lógica de clases conocida como teoría de conjuntos. Estos diagramas se usan para mostrar gráficamente la agrupación de cosas elementos en conjuntos, representando cada conjunto mediante un círculo o un óvalo. La posición relativa en el plano de tales círculos muestra la relación entre los conjuntos.

� Por ejemplo, si los círculos de los conjuntos A y B se solapan, se muestra un área común a ambos conjuntos que contiene todos los elementos contenidos a la vez en A y en B. Si el círculo del conjunto A aparece dentro del círculo de otro B, es que todos los elementos de A también están contenidos en B.

Conjunto universal: � El conjunto universal se representa por medio de un rectángulo, como marco de referencia del conjunto o de la operación que se quiere realizar:

� Los conjuntos no vacíos se representan por medio de curvas cerradas, indicando el nombre del conjunto en la parte externa:

Relaciones entre conjuntos: � Sobre las relaciones que se pueden establecer entre dos conjuntos, hemos visto dos básicas: Los conjuntos no tienen elementos comunes, luego el resultado es el conjunto vacío.

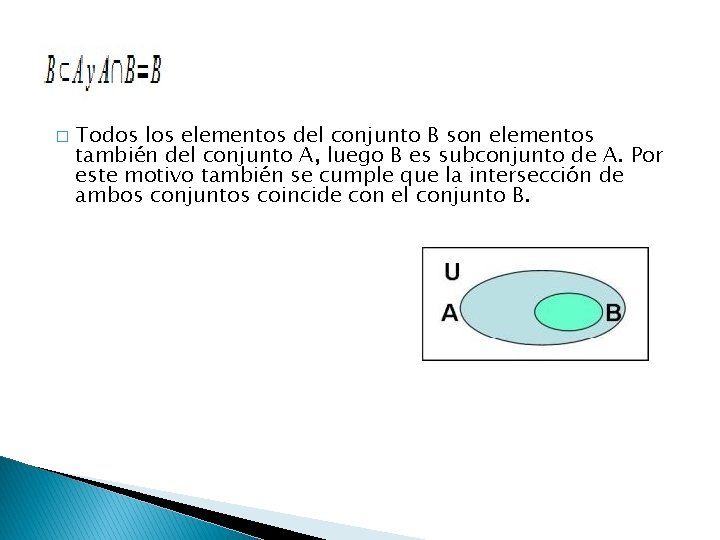
� Todos los elementos del conjunto B son elementos también del conjunto A, luego B es subconjunto de A. Por este motivo también se cumple que la intersección de ambos conjuntos coincide con el conjunto B.

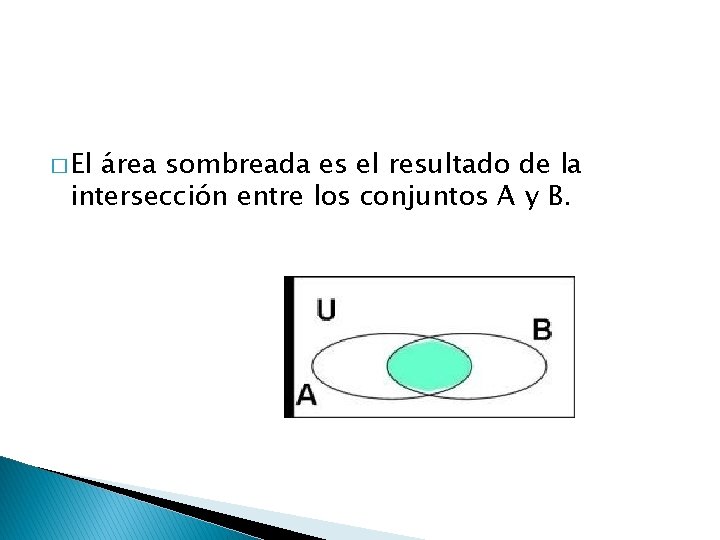
� El área sombreada es el resultado de la intersección entre los conjuntos A y B.

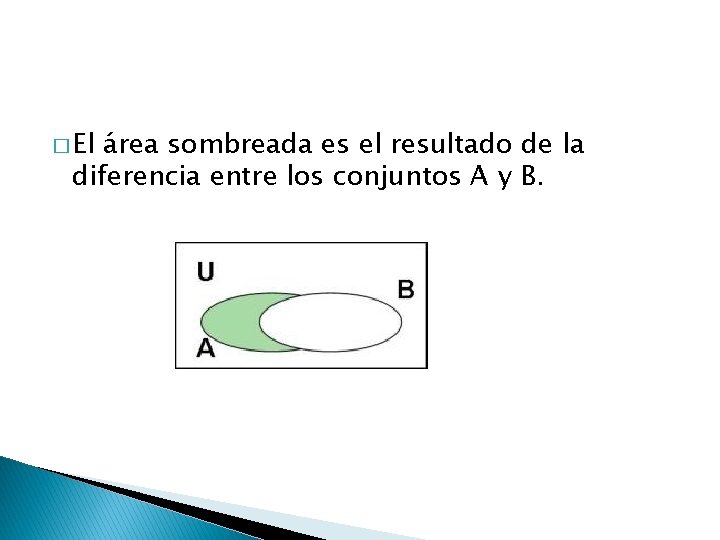
� El área sombreada es el resultado de la diferencia entre los conjuntos A y B.

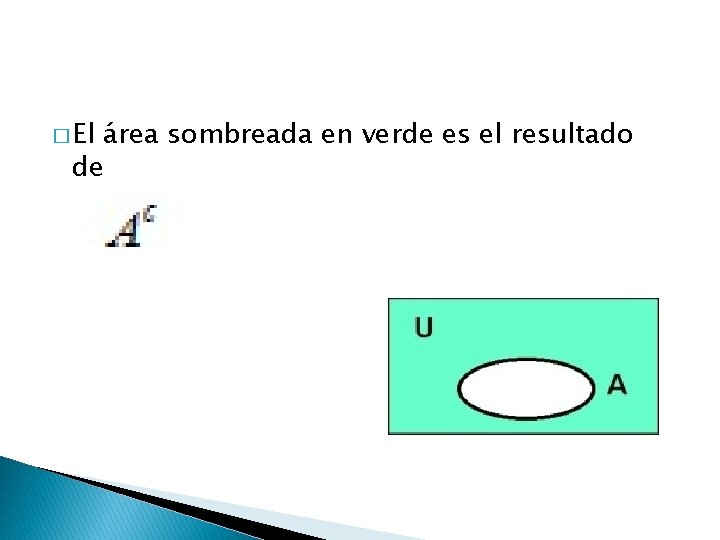
� El área sombreada en verde es el resultado de

2. 4 Probabilidad con técnicas de conteo: Axiomas , teoremas. � � � *Axiomas** Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por Kolmogórov en 1933. Los axiomas de la formulación moderna de la teoría de la probabilidad constituyen una base para deducir a partir de ellas un amplio número de resultados. La letra P se utiliza para designar la probabilidad de un evento, siendo P(A) la probabilidad de ocurrencia de un evento A en un experimento.

� � AXIOMA 1 Si A es un evento de S, entonces la probabilidad del evento A es: 0 ≤ P(A) ≤ 1 Como no podemos obtener menos de cero éxitos ni más de n éxitos en n experimentos, la � probabilidad de cualquier evento A, se representa mediante un valor que puede variar de 0 a 1. � AXIOMA 2 � � � � � Si dos eventos son mutuamente excluyentes, la probabilidad de obtener A o B es igual a la probabilidad de obtener A más la probabilidad de obtener B. P(A ∪ B) = P(A) + P(B) Excluirse mutuamente quiere decir que A y B no pueden ocurrir simultáneamente en el mismo experimento. Así, la probabilidad de obtener águila o sol en la misma tirada de una moneda será P(A ∪ B) = P(A) + P(B) P(A ∪ B) = 1/2 + 1/2 = 1. En general podemos decir que la suma de las probabilidades de todos los posibles eventos mutuamente excluyentes es igual a 1: � P(A 1) + P(A 2) + P(A 3) +. . . + P(An) = 1 � AXIOMA 3 � � � Si A es un evento cualquiera de un experimento aleatorio y A’ es el complemento de A, entonces: P(A’) = 1 - P(A) Es decir, la probabilidad de que el evento A no ocurra, es igual a 1 menos la probabilidad de que ocurra.

TEOREMAS** TEOREMA 1. Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero. p(f)=0

� DEMOSTRACIÓN: � Si sumamos a fun evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD � TEOREMA 2. La probabilidad del complemento de A, Ac debe ser, p(Ac)= 1 – p(A)

� DEMOSTRACIÓN: � Si sumamos a fun evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD � TEOREMA 2. La probabilidad del complemento de A, Ac debe ser, p(Ac)= 1 – p(A)

2. 5 probabilidad condicional : dependiente , independiente. � � Eventos Independientes Dos o más eventos son independientes cuando la ocurrencia o no -ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo. Dos eventos, A y B, son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro.

� Por definición, A es independiente de B si y sólo si: A y B, son independientes si la ocurrencia de uno no tiene que ver con la ocurrencia de otro. Por definición, A es independiente de B si y sólo si: (Pn. A)=P(A)P(B)

Eventos dependientes Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P (A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.

� Se debe tener claro que A|B no es una fracción. P (A|B) = P(A y B) / P (B) o P (B|A) = P(A y B) / P(A) Probabilidad Condicional = P(A y B) / P (B) o P (B|A) = P(A y B) / P(A)

2. 6 Ley multiplicativa. � Al multiplicar la formula P(B/A) =P( A Ç B)/ P(A) por P( A); obtenemos la siguiente regla multiplicativa, esta es importante por que nos permite calcular la probabilidad de que ocurran dos eventos. � Teorema: si un experimento pueden ocurrir los eventos A y B, entonces P( A Ç B)= P( A) P(B/A). así la probabilidad de que ocurran A y B es igual a la probabilidad de que ocurra A multiplicada por la probabilidad de que ocurra B, dado que ocurre A.

� Ø Si los eventos A y B son dependientes: Ø Si los eventos A y B son independientes:

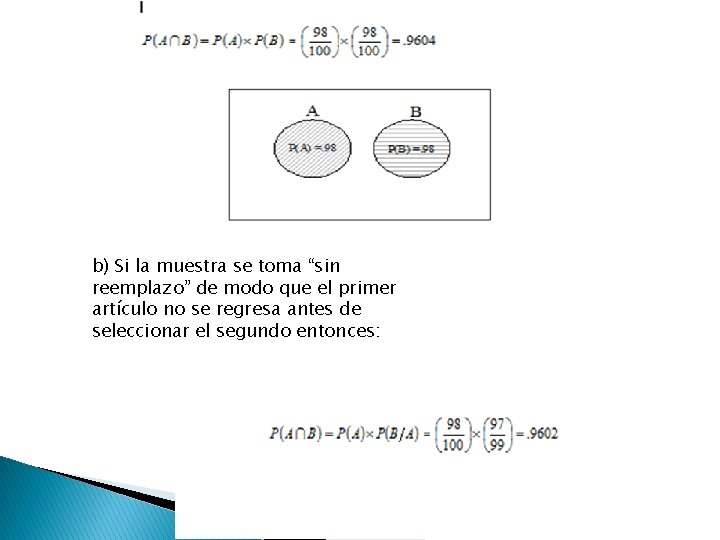
� Ejemplo 1: Se selecciona una muestra aleatoria n = 2 de un lote de 100 unidades, se sabe que 98 de los 100 artículos están en buen estado. La muestra se selecciona de manera tal que el primer artículo se observa y se regresa antes de seleccionar el segundo artículo (con reemplazo), a) calcule la probabilidad de que ambos artículos estén en buen estado, b) si la muestra se toma sin reemplazo, calcule la probabilidad de que ambos artículos estén en buen estado. � A: El primer artículo está en buen estado. � B: El segundo artículo está en buen estado.

b) Si la muestra se toma “sin reemplazo” de modo que el primer artículo no se regresa antes de seleccionar el segundo entonces:

2. 7 Eventos independientes: regla de Bayes. � Regla de Bayes. � Sea d un espacio muestral que está formado por los eventos A 1, A 2, A 3, . . . , An mutuamente excluyentes, luego, � d = A 1ÈA 2ÈA 3È. . . ÈAn

� Luego si ocurre un evento B definido en d, observamos que; � B = dÇB = (A 1ÈA 2ÈA 3È. . . ÈAn)ÇB = (A 1ÇB)È(A 2ÇB)È(A 3ÇB)È. . . È(AnÇB) � Donde cada uno de los eventos AiÇB son eventos mutuamente excluyentes, por lo que � p(B) = p(A 1ÇB) + p(A 2ÇB) + p(A 3ÇB) +. . . + p(AnÇB) � � � y como la p(AiÇB) = p(Ai)p(B½Ai) , o sea que la probabilidad de que ocurra el evento Ai y el evento B es igual al teorema de la multiplicación para probabilidad condicional, luego; p(B) = p(A 1)p(B½A 1) + p(A 2)p(B½A 2) + p(A 3)p(B½A 3) + p(An)p(B½An) Si deseamos calcular la probabilidad de que ocurra un evento Ai dado que B ya ocurrió, entonces;

� � La expresión anterior es el teorema de Bayes, que como se observa es una simple probabilidad condicional. Ejemplos: 1. Tres máquinas denominadas A, B y C, producen un 43%, 26% y 31% de la producción total de una empresa respectivamente, se ha detectado que un 8%, 2% y 1. 6% del producto manufacturado por estas máquinas es defectuoso, a. Se selecciona un producto al azar y se encuentra que es defectuoso, ¿cuál es la probabilidad de que el producto haya sido fabricado en la máquina B? , b. Si el producto seleccionado resulta que no es defectuoso, ¿cuál es la probabilidad de que haya sido fabricado en la máquina C? Solución: Para resolver este problema nos ayudaremos con un diagrama de árbol;

� a. Definiremos los eventos; D = evento de que el producto seleccionado sea defectuoso (evento que condiciona) � A = evento de que el producto sea fabricado en la máquina A � B = evento de que el producto sea fabricado por la máquina B � C = evento de que el producto sea fabricado por la máquina C � P(B½D) = p(BÇD)/p(D) = p(B)p(D½B)/p(A)p(D½A) + p(B)p(D½B) + p(C)p(D½C) � P(B½D) = (0. 26*0. 02)/(0. 43*0. 08 + 0. 26*0. 02 + 0. 31*0. 016) = 0. 0052/0. 04456 � =0. 116697 b. ND = evento de que el producto seleccionado no sea defectuoso (evento que condiciona) � A = evento de que el producto sea fabricado en la máquina A � B = evento de que el producto sea fabricado por la máquina B � C = evento de que el producto sea fabricado por la máquina C � P(C½ND)=p(CÇND)/p(ND)=p(C)p(ND½C)/p(A)p(ND½A) + p(B)p(ND½B) + p(C)p(ND½C) = 0. 31*0. 984/(0. 43*0. 92 + 0. 26*0. 98 + 0. 31*0. 984) = 0. 30504/0. 95544 � =0. 31927