Nociones Elementales de Matrices n Antes de ver

Nociones Elementales de Matrices n Antes de ver la solución de los Sistemas de Ecuaciones Lineales haremos un repaso de las fundamentos de las matrices. 1

Nociones Elementales de Matrices 2

Nociones Elementales de Matrices 3

Nociones Elementales de Matrices 4

Nociones Elementales de Matrices 5

Nociones Elementales de Matrices 6

Nociones Elementales de Matrices 7

Solución de sistemas de ecuaciones lineales n n n Análisis de Circuitos (ecuaciones de malla y nodos) Solución Numérica de ecuaciones diferenciales (Método de las diferencias Finitas) Solución Numérica de ecuaciones de integrales (Metodo de los Elementos Finitos, Método de los Momentos) 8

Consistencia (Solubilidad) n n El sistema lineal de ecuaciones Ax=b tiene una solución, o es consistente si y solo si Rango{A}=Rango{A|b} Un sistema es inconsistente cuando Rango{A}<Rango{A|b} Rank{A} es el máximo numero de columnas linealmente independientes o filas de A. El rango puede ser encontrado usando ERO (Elementary Row Oparations) ó ECO (Elementary column operations). 9

Operaciones Elementales de filas (ERO) n Las siguientes operaciones aplicadas a la matriz aumentada[A|b], producen un sistema lineal equivalente n Intercambios: El orden de dos filas pueden ser cambiada n Escalado: Multiplicando un fila por una constante no cero n Reemplazo: Las filas pueden ser reemplazadas por la suma de esa fila y un múltiplo distinto a cero de cualquier otra fila 10

Un ejemplo inconsistente ERO: Multiplicar la primera fila por -2 y sumar la segunda fila Rank{A}=1 Rank{A|b}=2 Entonces este sistema de ecuaciones no es soluble 11

Unicidad de las soluciones n El sistema tiene una única solucion si y solo si Rango{A}=Rango{A|b}=n n es el orden del sistema n Tales sistemas son llamados sistemas full-rank (rango completo) 12

Sistemas rango completo (Full-rank) n Si Rango{A}=n Det{A} 0 A es nonsingular por lo tanto invertible Solución Única 13

Matrices de rango deficiente n Si Rango{A}=m<n Det{A} = 0 A is singular por lo tanto no es invertible número infinito de soluciones (n-m variables libres) sistema sub-determinado Rank{A}=Rank{A|b}=1 Consistente soluble 14

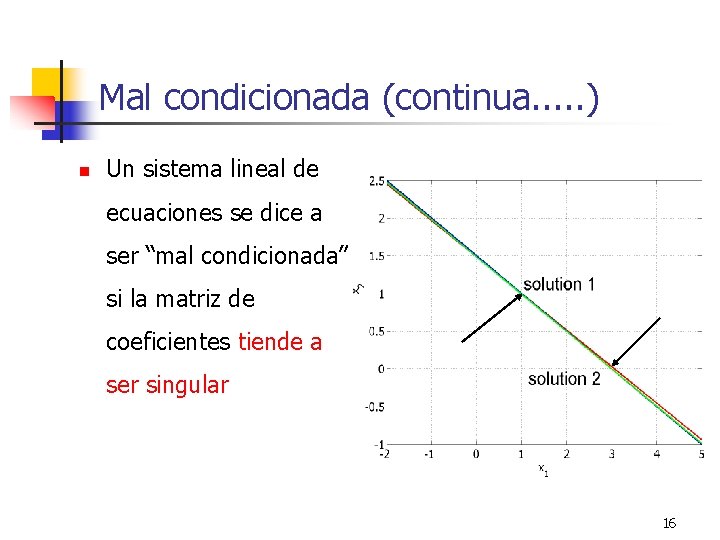
Sistema de ecuaciones mal-condicionadas n Una pequeña desviación en las entradas de la matriz A, causa una gran desviación en la solución. 15

Mal condicionada (continua. . . ) n Un sistema lineal de ecuaciones se dice a ser “mal condicionada” si la matriz de coeficientes tiende a ser singular 16

17

Tipos de ecuaciones de sistemas lineales a ser estudiados n Los coeficientes reales de la matriz cuadrada A n EL vector b es diferente de cero y real n Sistema consistente, soluble n Sistemas rango completo, solución única n Sistemas bien-condicionados 18

Técnicas de Solución n Métodos directos de solución n Encuentra una solución en un número finito de operaciones transformando el sistema en un sistema equivalente que sea ' más fácil ' de solucionar. Triangulares diagonales, . Métodos de solución Iterativos n n Calcula las aproximaciones sucesivas del vector solución para una mat. A y un b dados, comenzando de un punto inicial x 0 Total del · de operaciones es incierto, puede que no converja. 19

Métodos de solución directa Eliminación Gaussiana n n Usando ERO, la matriz A es transformada en una matriz triangular superior (todos los elementos debajo de la diagonal son cero). Sustitución hacia atrás es usada para resolver un sistema triangular superior ERO Back substitution n 20

Primer paso de la eliminación Elemento pivotal 21

Segundo paso de la eliminación Elemento Pivotal 22

Algoritmo de la Eliminación Gaussiana Define un número de pasos como p (fila pivotal) For p=1, n-1 For r=p+1 to n For c=p+1 to n 23

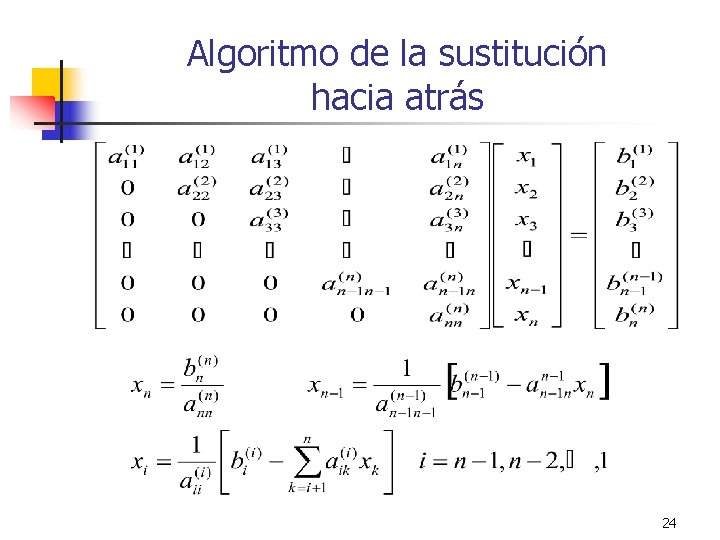
Algoritmo de la sustitución hacia atrás 24

Contador de Operaciones n Número de operaciones aritméticas requeridas por el algoritmo para completar esta tarea. Generalmente solo multiplicaciones y divisiones son contadas. Proceso de Eliminación n Sustitución hacia atrás n Total n n Dominates No eficiente para diferentes vectores RHS 25

Decomposición LU A=LU Ax=b LUx=b Define Ux=y Ly=b Resolver y por sustitución hacia adelante Ux=y Resolver x por sustitución hacia atrás Las operaciones elementales entre filas debe ser desarrolladas en b así como en A. La información de estas operaciones es almacenada en L En verdad y es obtenida aplicando operaciones elementales al vector b. 26

Decomposición LU por Eliminación Gausiana Existen infinitas formas diferentes para descomponer A. Una de las más populares es: U=Matriz de la Eliminación Gaussiana L=Multiplicadores usados para la eliminación Almacenamiento Compacto: Las entradas diagonales de la matriz L son todos unos, estos no necesitan almacenarse. LU es almacenado en una matriz. 27

Contador de Operaciones n A=LU Descomposición n Ly=b Sustitución hacia adelante n Ux=y Sustitución hacia atrás n Total n Para diferentes vectores RHS, el sistema puede ser eficientemente resuelto. 28

Pivoteo n n n Computadoras usan precisión aritmética finita Pequeños errores son introducidos en cada operación aritmética, propagación de errores Cuando los elementos pivotales son muy pequeños, los multiplicadores podrían ser muy grandes. La adición de números de magnitud diferente puede conducir a la pérdida de significación. Para reducir el error, se realiza intercambio de filas para maximizar la magnitud del elemento pivotal. 29

Ejemplo: Sin Pivoteo aritmética 4 -digit Pérdida de precisión 30

Ejemplo: Con Pivoteo 31

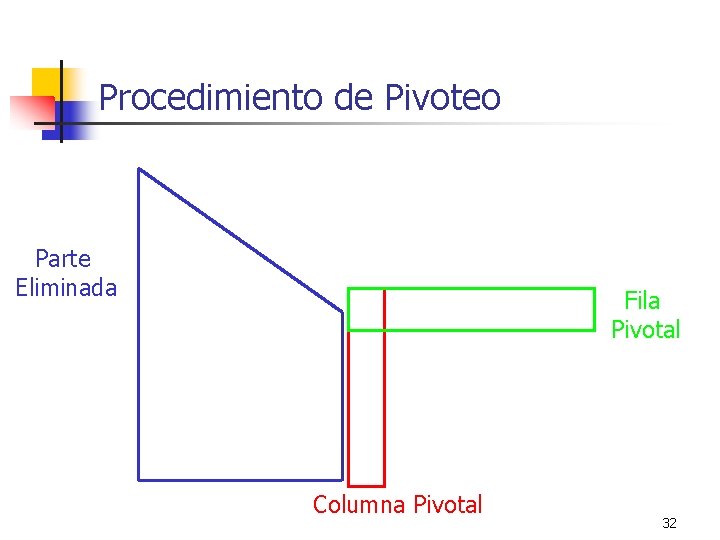
Procedimiento de Pivoteo Parte Eliminada Fila Pivotal Columna Pivotal 32

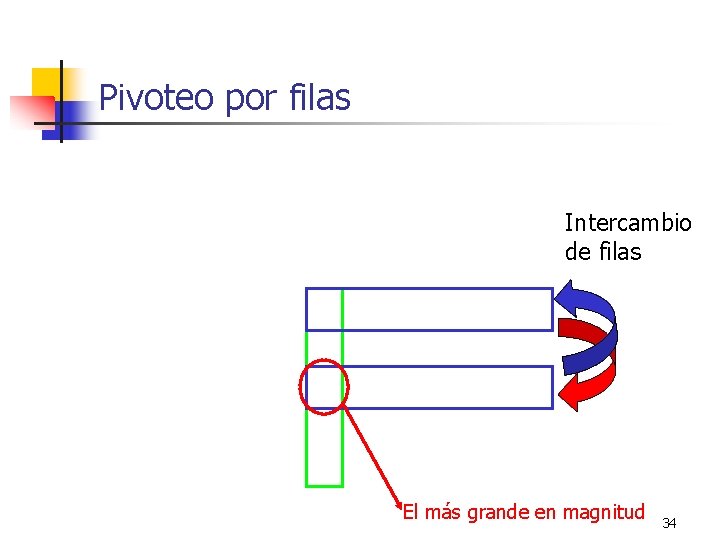
Pivoteo por fila n Más comúnmente llamado procedimiento de pivoteo parcial n Busque la columna pivotal n Encuentre el mas grande elemento en magnitud n Luego intercambie esta fila con la fila pivotal. 33

Pivoteo por filas Intercambio de filas El más grande en magnitud 34

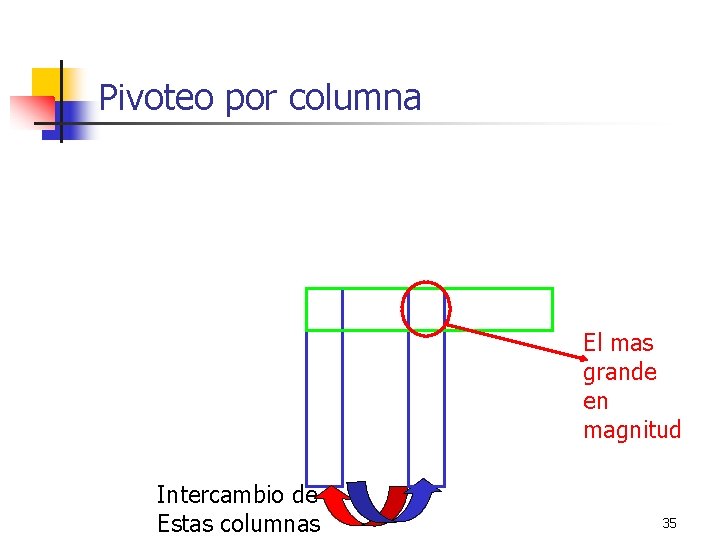
Pivoteo por columna El mas grande en magnitud Intercambio de Estas columnas 35

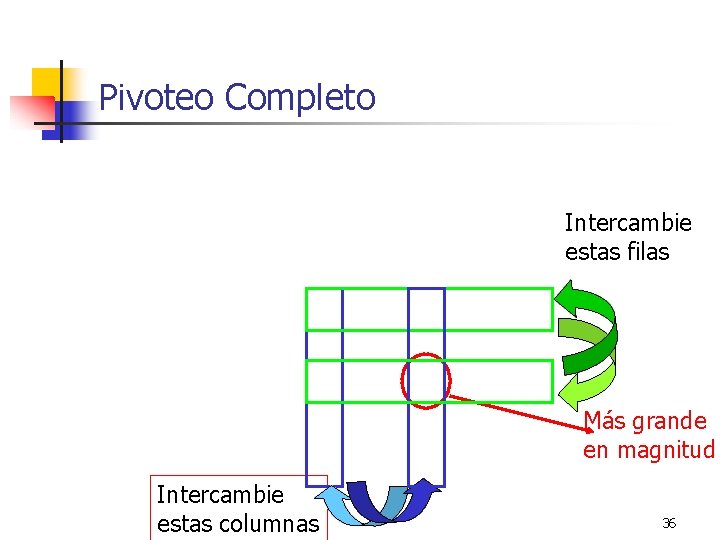
Pivoteo Completo Intercambie estas filas Más grande en magnitud Intercambie estas columnas 36

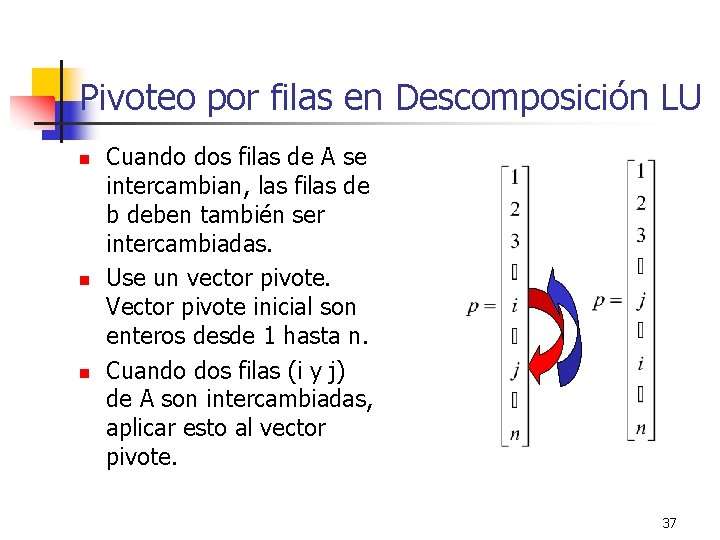
Pivoteo por filas en Descomposición LU n n n Cuando dos filas de A se intercambian, las filas de b deben también ser intercambiadas. Use un vector pivote. Vector pivote inicial son enteros desde 1 hasta n. Cuando dos filas (i y j) de A son intercambiadas, aplicar esto al vector pivote. 37

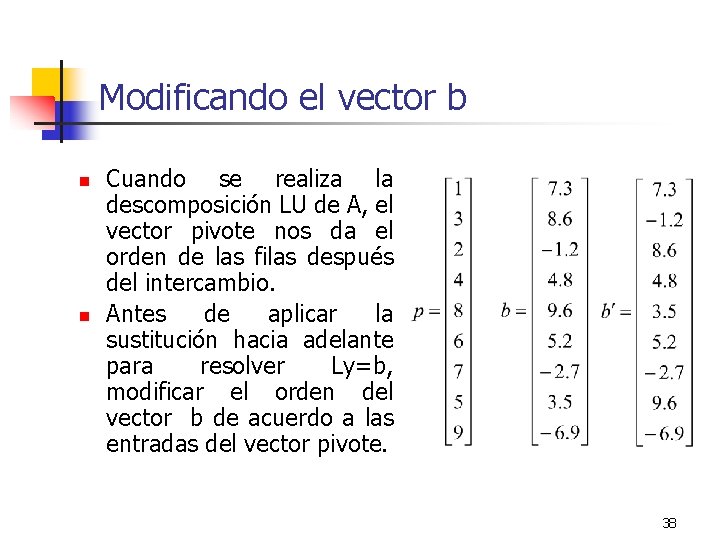
Modificando el vector b n n Cuando se realiza la descomposición LU de A, el vector pivote nos da el orden de las filas después del intercambio. Antes de aplicar la sustitución hacia adelante para resolver Ly=b, modificar el orden del vector b de acuerdo a las entradas del vector pivote. 38

Descomposición LU algoritmo con pivoteo parcial columna a ser eliminada For k=1, n-1 p=k For r=k+1 to n if if p>k then For c=1 to n For r=k+1 to n Columna para una entrada máxima Intercambio de filas Actualizando la matriz L Actualizando la matriz U For c=k+1 to n 39

Ejemplo Intercambio de columnas: Máxima magnitud segunda fila Intercanbio de la 1 era y 2 da fila 40

Ejemplo (continuación). . . Elimación de a 21 y a 31 usando a 11 como elemento pivotal A=LU en forma compacta (en una sola matriz) Multiplicadores (matriz L) l 21=0; l 31=-0. 25 41

Ejemplo (continuación). . . Columna encontrada: Maxima magnitud en la tercera fila Intercambio de la 2 da y 3 era fila 42

Ejemplo (continuación). . . Eliminar a 32 usando a 22 como elemento pivotal Multiplicadores (matriz L) l 32=3/3. 5 43

Ejemplo (continuación). . . A’x=b’ LUx=b’ Ux=y Ly=b’ 44

Ejemplo (continuación). . . Ly=b’ Sustitución Inversa Ux=y Sustitución Directa 45

Eliminación de Gauss-Jordan n Los elementos sobre la diagonal se convierten y por debajo de la diagonal son ceros. 46

Eliminación de Gauss-Jordan n Casi 50% mas de operaciones aritméticas que la Eliminación Gaussiana. Gauss-Jordan (GJ) Eliminación es preferible cuando la inversa de una matriz es requirido. Aplicar eliminación GJ para convertir A en una matriz identidad. 47

Diferentes formas de factorización LU n Forma de Doolittle Obtenida por Eliminación Gaussiana n Forma de Crout n Forma de Choleski 48

Forma de Crout n Cálculo de la primera columna de L n Cálculo de la primera fila de U n Cálculo alternado de las colum. de L y filas de U 49

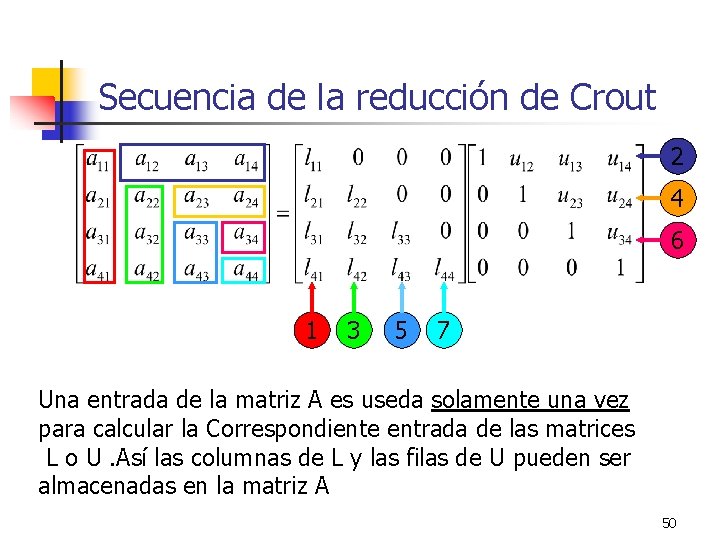
Secuencia de la reducción de Crout 2 4 6 1 3 5 7 Una entrada de la matriz A es useda solamente una vez para calcular la Correspondiente entrada de las matrices L o U. Así las columnas de L y las filas de U pueden ser almacenadas en la matriz A 50

Factorización de Choleski n n n Si A es simétrica y definida positiva, entonces la factorización LU Puede ser arreglada para que U = LT , la cual se obtiene de la factorización de Choleski A = LLT Donde L es una matriz triangular inferior con diagonal con entradas positivas Algoritmo para el cálculo puede ser derivado por la ecuación correspondiente a las entradas de A y LLt En el caso de 2 × 2, por ejemplo, Implica que: 51

Factorización de Choleski (continua) n Una forma de escribir el algoritmo general, es 52

Solución de Sistemas Lineales de ecuaciones Complejas Cz=w C=A+j. B Z=x+jy w=u+jv (A+j. B)(x+jy)=(u+jv) (Ax-By)+j(Bx+Ay)=u+jv Sistema lineal de ecuaciones reales 53

Sistemas grandes y Esparcidos n n Cuando el sistema lineal es grande y esparcido (muchas entradas ceros), los métodos directos llegan a ser ineficientes por la presencia de términos de relleno. Los términos de relleno son aquellos que resultan ser diferentes de cero durante la eliminación Términos de relleno Eliminación 54

Matrices Esparcidas n n La matriz de ecuación de nodos es una matriz esparcida. Matrices Esparcidas son almacenadas eficientemente almacenando solamente las entradas no cero. Cuando del sistema es muy grande (n=10, 000) los términos de relleno aumentan los requerimientos de almacenamiento considerablemente. En tales casos los métodos de solución iterativa debe ser preferidos en lugar de métodos de solución directa. 55

Problema 1 n n Resolver por Eliminación Gaussiana con pivoteo parcial de filas: E 2 -(3/4)E 1 =>E 2 E 3 -(1/2)E 1 =>E 3 E 4 -(-1/4)E 1=>E 4 56

Problema 1 n n n Intercambiamos las Ecuaciones 2 y 3 (E 2 E 3) E 3 -(-1/2)E 2 =>E 3 E 4 -( 1/4)E 2 =>E 4 57

Problema 1 n n E 4 -(-1/4)E 3 =>E 4 Resolviendo por sustitución hacia atrás: 58

Problema 2 n n Obtener la factorización de Doolite: Solución 1 A partir de la Eliminacion Gaussiana: m 21= a 21/a 11 =2/6=1/3 E 2 -(1/3)E 1=>E 2 59

Problema 2 n Solución 2 Planteando el producto matricial: 60

Problema 3 n n n Resolver por la factorización de Doolite: Solución Del ejercicio anterior ya tenemos la factorización LU: 61

Problema 3 Se obtienen dos sistemas triangulares fáciles de resolver. Resolviendo el sistema triangular inferior por sustitución directa: Resolviendo el sistema triangular superior por sustitución directa: 62

Problema 4 n Obtener la factorización de Crout: Solucion Debemos plantear la multiplicacion matricial: 63

Problema 4 64

Problema 5 Método de Crout para sistemas tridiagonales 65

Problema 6 Factorizar por el método de Choleski la siguiente matriz: Solución Se requiere que la matriz sea simétrica y definida positiva para aplicar Choleski. 66

Problema 6 Es evidente que la matriz es simétrica; para verificar que es definida positiva verificamos si se satisface el criterio de Silvester: 67

Problema 6 Dado que los determinantes de todos los menores principales son positivos podemos afirma que la matriz es definida positiva y podemos aplicar la factorización de Choleski con seguridad. 68

Problema 6 Resolviendo la multiplicación matricial: 69