Variazioni nel piano i numeri complessi e le




























































- Slides: 65

Variazioni nel piano: i numeri complessi e le trasformazioni geometriche

Perché ampliare i numeri reali? l L’insieme dei numeri reali ha una “struttura” matematica che permette di risolvere moltissimi problemi, ma è insufficiente nella risoluzione di equazione del tipo:

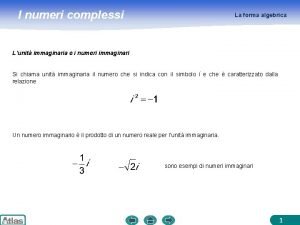
E se provassimo a risolvere queste equazioni? Unità immaginaria e numeri immaginari l Chiamiamo i una soluzione dell’equazione l i si chiama unità immaginaria. Vale che i² = -1, l Chiamiamo numeri immaginari “ il prodotto fra numeri reali e unità immaginaria” 2 i… -4 i … -i … In questo modo si risolve il problema dell’estrazione di radice di un numero reale negativo

Numeri complessi in forma algebrica Un numero complesso z si scrive nella forma z = x+iy Dove x, y sono numeri reali: l x è la parte reale l y è la parte immaginaria l Questi sono gli elementi dell’insieme numerico di cui ci occupiamo

Somma e sottrazione Somma (legge di composizione interna a C): (a + ib)+(c + id)=(a + c)+ i(b + d) Questa operazione ha le seguenti proprietà: l Estende la consueta operazione di somma tra reali; l Gode della proprietà associativa e commutativa. l Esiste l’elemento neutro 0 l Ogni elemento z=a+ib ammette in C un “simmetrico” rispetto all’addizione (-z=a-ib) che si chiama opposto di z. l Sottrazione (legge di composizione interna) (a + ib) - (c + id) = (a-c)+ i (b-d) l

Come definire la moltiplicazione? Ipotesi di lavoro… Cerchiamo di definire il prodotto (a + ib) · (c + id) Richiediamo le seguenti cose: 1. Deve estendere il prodotto tra numeri reali; 2. Deve soddisfare la proprietà i² = -1; 3. Deve essere commutativo e associativo; 4. Deve godere della proprietà distributiva della somma;

Costruiamo tale prodotto (a + i 0) ·(b + i 0) = a · b l a ·(ib) = (ib) · a = i(ab)= i(ba) l (ia) · i = i ·(ia) = (i · i) · a = -a l (ia) · (ib) = (ib) · (ia) = (i ·i)(ab)= - ab E infine … (a + ib) ·(c + id) = (a + ib) · c + (a + ib) ·(id) = = [ac + i(bc)] + [i(ad)+ (ib) ·(id)] = = ac + i(bc) + i(ad) – bd = (ac – bd) + i(bc + ad) l

Coniugato … l E’ utile definire a questo punto anche il numero complesso coniugato di un numero. come quel numero, indicato con , come quel numero complesso che ha la stessa parte reale di z e parte immaginaria opposta:

… e reciproco l Ogni elemento z = a + ib , con a e b non contemporaneamente nulli, ammette in C un “simmetrico” rispetto alla moltiplicazione, che si chiama reciproco di z , dato da

Divisione tra complessi l La divisione in C è introdotta grazie alla presenza del reciproco di un numero complesso (non nullo). La scrittura l (con c e d non entrambi nulli) indicherà il seguente prodotto:

Rappresentazione geometrica: come punti del piano… Fissato un sistema di riferimento cartesiano ortogonale con assi x e y, e un numero complesso u= x + iy , i numeri reali x e y si possono interpretare come l’insieme vettori , dove P è il punto di coordinate (x, y) e O è l’origine degli assi

l Il piano ottenuto si chiama di Argand-Gauss o piano di Gauss. l L’asse delle ascisse viene anche chiamato asse reale e quello delle ordinate asse immaginario. l Il modulo di un numero complesso rappresenta la lunghezza del vettore che rappresenta u. l |u-v| rappresenta la lunghezza del vettore

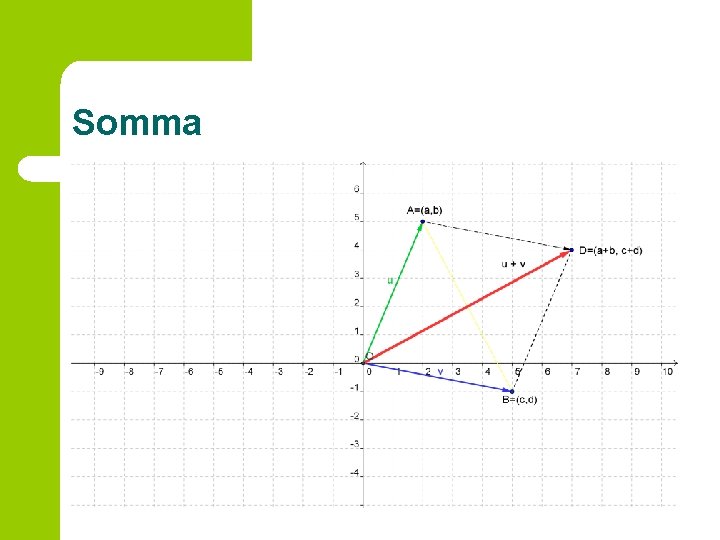
Somma Se i due numeri complessi u=a+ib e v=c+id sono visti come i vettori e , con A=(a, b) e B=(c, d), la loro somma è realizzata graficamente traslando il vettore in modo che parta dal punto A invece che da O. Tale regola si chiama regola del parallelogramma. Il vettore risultante sarà tale che D=(a+b, c+d) ( le coordinate di D sono la somma delle coordinate di A e B)

Somma

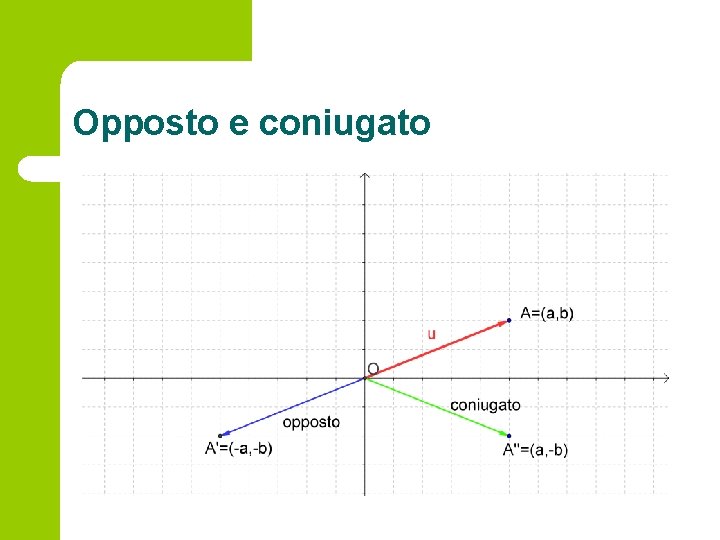
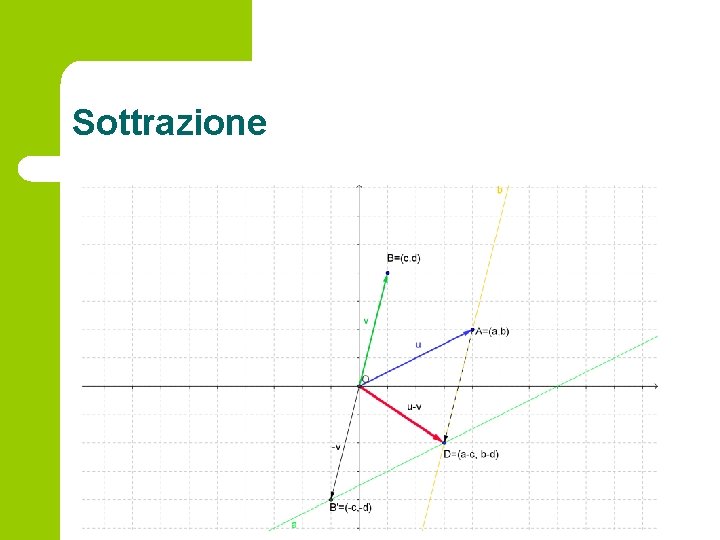
L’opposto –u è realizzato graficamente come il vettore Opposto simmetrico ad rispetto ad O. l A’= (-a, -b) l La sottrazione u-v non è altro che la somma (vettoriale) di u con l’opposto di v (a, b)-(c, d)=(a-b, c-d) l Il coniugato di u è rappresentato come il vettore ad rispetto all’asse reale. A’’= (a, -b) simmetrico

Opposto e coniugato

Sottrazione

Interpretazione della moltiplicazione: Moltiplicazione a coefficienti interi l Se n è un intero positivo, si definisce il complesso nu come la somma di u con se stesso n volte e –nu come la somma di –u con se stesso n volte l Geometricamente, stiamo considerando i multipli interi del vettore dato


Moltiplicazione fra un numero reale e un numero complesso l Siano C=(c, 0) e Z=(a, b). I vettori e rappresentano rispettivamente un numero reale c e un numero complesso z=a+ib. Considero la moltiplicazione fra e : sarà un nuovo vettore , dove Z’=(ca, cb)

Interpretazione geometrica l l Considero il vettore , dove C=(c, 0), e il vettore , dove Z=(a, b), con b non nullo. Congiungo il punto A=(1, 0) con Z, considero la semiretta per O e Z, uscente da Z. Considero la semiretta uscente dal punto C e parallela alla semiretta per O e Z: le due semirette si incontrano in punto Z’. è proprio il vettore cercato e si ottiene partendo da con un’omotetia di centro O e fattore c

Perché? l l l Devo provare che Z’=(ca, cb). Il segmento misura 1, il segmento misura |c| e il segmento misura Utilizzando il teorema di Talete (similitudine tra i triangoli OAZ e OCZ’) abbiamo che l l Ossia l Z’ giace sulla semiretta per O e Z, la sua distanza da O è |c| volte quella di Z da O, dunque le sue coordinate saranno |c| volte le coordinate di Z: dunque Z’=(ca, cb)


Moltiplicazione per i: interpretazione l Considero z=a+ib geometrica l i*z= b- ia Chiamo A=(a, b) e A’=(b, -a) Considero i vettori e Considero la retta passante per O e A: ha equazione l Considero la retta passante per O e A’: ha equazione l Le due rette hanno i coefficienti angolari che sono l’uno l’opposto del reciproco dell’altro: sono ortogonali I due vettori hanno chiaramente la stessa lunghezza l l

Moltiplicazione per i: interpretazione geometrica l Moltiplicare per i significare ruotare in senso antiorario il vettore z di un angolo di 90°


Forma trigonometrica (immagini tratte dal sito de “Il Giardino di Archmede”) y z |z| si chiama modulo di z |z| θ x θ si chiama argomento di z o • Il modulo di z si indica con |z| • L’argomento principale (quello compreso tra 0 e 2Π) con arg(z) Da z=x+iy si passa a

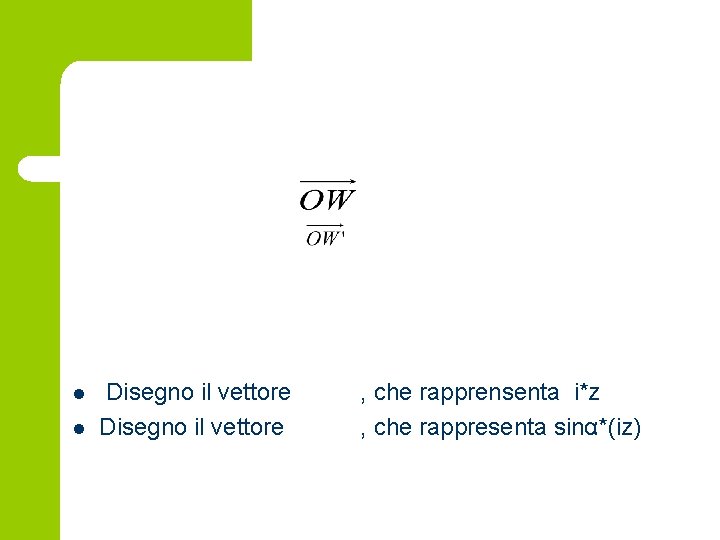
l Dati prodotto u*z e , considero il Moltiplicazione complessi di modulo 1 u*z= cosα* z + sinα*(i* z) Interpretiamo questa scrittura in termini geometrici: l l l Si considera il vettore , con A=(cosα, sinα) e il vettore Considero il vettore , dove A’=(cosα, 0) Faccio la moltiplicazione cosα*z e ottengo il vettore


l l Disegno il vettore , che rapprensenta i*z , che rappresenta sinα*(iz)


l Si sommano i due vettori


l l Il triangolo POZ’ è rettangolo Il cateto misura |cosα||z| , il cateto misura |sin α| |z|: Dunque misura |z|: dunque il vettore è isometrico al vettore Per β=Z’OP vale con α compreso tra 0 e 2π

Ci sono quattro casi : l Primo caso: allora β= α, ZOP=ZOP’ e OP si ottiene da OZ ruotando in senso antiorario di un angolo pari ad α


l l Secondo caso: allora β= π- α, ZOP= π- β= α e OP si ottiene da OZ ruotando in senso antiorario di un angolo pari ad α


l l Terzo caso: allora β= α-π, ZOP= π+ β= α e OP si ottiene da OZ ruotando in senso antiorario di un angolo pari ad α


l Quarto caso: allora β= 2π –α, ZOP= 2π- β= α e OP si ottiene da OZ ruotando in senso antiorario di un angolo pari ad α


Moltiplicazione per complesso di modulo 1 Si ottiene quindi una rotazione antioraria attorno a O di un angolo pari ad α=Arg(u)


Un nuovo modo di ricavare le formule di addizione l l l Considero u=cosα + i sinα e v=cosβ + i sinβ due complessi di modulo 1. Ad essi si associano rot(α) e rot(β) le due rotazioni antiorarie attorno a O rispettivamente di α e β. Se effettuiamo prima rot(α) e poi rot(β), questo equivale a compiere una rotazione antioraria attorno a 0 di un angolo pari a α+β

Nel linguaggio dei numeri complessi, questo significa che per ogni z numero complesso , [(cosα+ isinα)(cosβ+ isinβ)]z=(cosα+ isinα)[(cosβ+ isinβ)z]=[cos(α+β)+i sin(α+β)]z. Ponendo z=1, abbiamo l [cos(α+β)+i sin(α+β)]=[(cosα+ isinα)(cosβ+ isinβ)] Eseguendo i calcoli e uguagliando parte reale e immaginaria, abbiamo [cos(α+β)+i sin(α+β)]=[(cosα cosβ – sinα sinβ) + i(sinα cosβ+ cosα sinβ)]

Otteniamo infine: cos(α+β) = cosα cosβ – sinα sinβ sin(α+β) = sinα cosβ+ cosα sinβ

Significato geometrico della moltiplicazione: ricapitoliamo Se u=|u|(cosα+isinα) e z è un altro numero complesso, la moltiplicazione uz=|u|[(cosα+isinα)z] è la composizione di una rotazione con centro nell’origine e di un’omotetia di fattore |u| con centro in O, ossia una roto-omotetia. l

Moltiplicazione in forma trigonometrica Eseguendo la moltiplicazione e ricordando le formule di addizione del coseno e del seno Il modulo si ottiene moltiplicando i moduli L’argomento si ottiene addizionando gli argomenti


Divisione di numeri complessi Forma Algebrica Forma Trigonometrica Il modulo si ottiene dividendo i moduli L’argomento si ottiene sottraendo gli argomenti

Potenze e radici intere di numeri complessi l Usando la forma trigonometrica dei numeri complessi e le proprietà della moltiplicazione si ottiene la cosiddetta formula di De Moivre

l Utilizzando la formula di De Moivre si può dimostrare che ogni numero complesso non nullo z e per ogni numero naturale n, esistono n radici n-esime di z, ovvero esistono n numeri complessi w tali che l . Se , allora si dimostra che le radici nesime di z sono date dalla formula seguente: con k= 0, 1, 2, …. , n-1

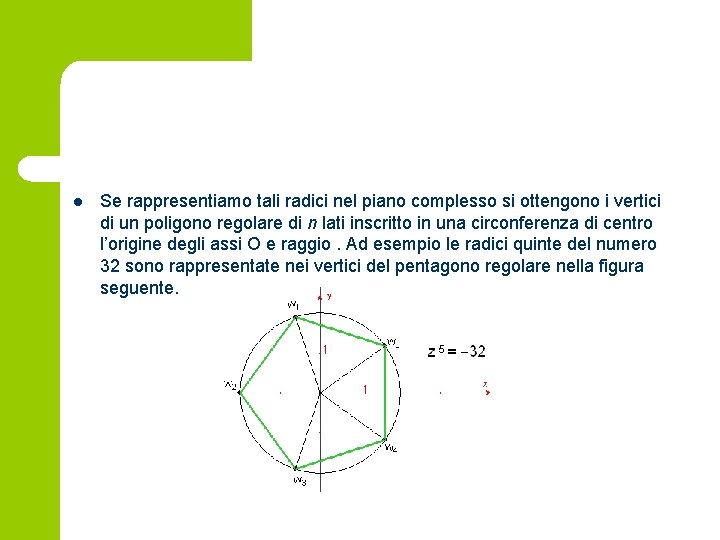
l Se rappresentiamo tali radici nel piano complesso si ottengono i vertici di un poligono regolare di n lati inscritto in una circonferenza di centro l’origine degli assi O e raggio. Ad esempio le radici quinte del numero 32 sono rappresentate nei vertici del pentagono regolare nella figura seguente.

Quindi possiamo concludere che: ogni numero complesso ammette n radici n-esime distinte l Nel caso particolare in cui z=1, si ottengono le radici nesime dell’unità: l l l con k= 0, 1, 2, …. , n-1. Esse hanno tutte modulo 1 e argomento che è un multiplo di e le loro immagini nel piano di Argand-Gauss sono date dai vertici di un poligono regolare inscritto nella circonferenza di centro l’origine degli assi e di raggio 1.


Risoluzione algebrica delle equazioni di secondo grado Consideriamo l’equazione dove è un numero reale. Si devono distinguere due casi; nel primo porta a determinare due soluzioni reali ( ), il secondo in cui , che conduce a due soluzioni complesse coniugate, dette immaginarie ( ). Quando invece si deve risolvere la generica equazione di secondo grado , con , si può seguire, una volta raccolto il coefficiente a, il “metodo del completamento del quadrato”, che fornisce le soluzioni con operazioni elementari sulle variabili e sui coefficienti reali:

l Posto , si hanno due casi: Δ≥ 0, allora e Δ<0, allora e Nel caso in cui l’equazione di partenza sia a coefficienti complessi, allora per risolvere l’equazione di secondo grado si risolve il sistema ottenuto uguagliando separatamente le parti reali dell’equazione e le parti immaginarie tra loro.


BREVE STORIA DEI NUMERI COMPLESSI l l La risoluzione di equazioni è un problema matematico molto antico. Risoluzione delle equazioni di secondo grado: metodo di “completamento del quadrato” noto sin dai tempi dei Babilonesi. Nel libro II degli Elementi di Euclide queste equazioni si trovano risolte sotto forma geometrica

L’equazione cubica l L’equazione cubica aveva sfidato per secoli i matematici: Luca Pacioli (1445 -1514) aveva sostenuto che la soluzione dell’equazione cubica generale era impossibile. l Fino al 1500 si era arrivati solo a risolvere dei casi particolari, senza riuscire a trovare un metodo generale. l Scipione Dal Ferro (1465 -1526), professore di matematica a Bologna, riuscì a risolvere le equazioni cubiche del tipo intorno al 1500; egli però non pubblicò il suo metodo risolutivo in quanto in tale periodo le scoperte venivano spesso tenute nascoste per poi sfidare i rivali a risolvere lo stesso problema. Tale metodo fu rivelato, alla fine della sua vita, ad un suo allievo, Antonio Maria Fior. l Anche Tartaglia (soprannome di Nicolò Fontana, 1500? -1559), aveva trovato un metodo per risolvere le equazioni di terzo grado del tipo e con p ed q positivi. Nel 1535 fu organizzata una sfida matematica tra Fior e Tartaglia. La notizia della brillante vittoria di Tartaglia nella sfida raggiunse Girolamo Cardano (1501 -1576). Tartaglia, date le insistenze di Cardano, finì per rivelargli il suo metodo, in cambio della promessa di mantenere tale metodo segreto.

Cardano… l l Nonostante questo impegno Cardano pubblicò la sua versione del metodo di risoluzione delle equazioni di terzo grado nella sua opera Ars Magna (Norimberga 1545). Lo stile di Cardano è piuttosto oscuro e la sua algebra è ancora allo stato retorico, in cui le equazioni vengono espresse quasi completamente a parole. La procedura risolutiva dell’equazione si ritrova descritta nelle celebri terzine di Tartaglia : "Quando che’l cubo con le cose appresso con p, q > 0. Se agguaglia à qualche numero discreto Trovan dui altri differenti in esso. Da poi terrai questo per consueto Che ‘l lor produtto sempre sia uguale Al terzo cubo delle cose neto, El residuo poi suo generale Delli lor lati cubi ben sottratti Varrà la tua cosa principale. ”

Rafael Bombelli (1526 -1573) l l l Bombelli, nella sua opera L’Algebra, divisa in tre libri, con la quale ciascuno da sé potrà venire in perfetta cognitione della teoria dell’Aritmetica (composta verso il 1560, ma stampata in parte solo nel 1572) si propose di completare i vari casi di risoluzione delle equazioni di terzo grado, anche nel caso irriducibile, cioè quando, nella formula di Cardano, si presenta la radice quadrata di un numero negativo. Bombelli prende in esame le radici immaginarie delle equazioni, che egli chiama "quantità silvestri", e giunge ad operare con i numeri che noi oggi chiamiamo "complessi". Bombelli stabilì le leggi formali di calcolo dei nuovi numeri, successivamente chiamati immaginari da Cartesio per indicare delle soluzioni considerate fittizie e irreali, né vere né “surde” (negative). Nell’Algebra troviamo la corretta trattazione di alcune equazioni di terzo grado che, se risolte con il procedimento di Cardano, Dal Ferro e Tartaglia, portano a radicali doppi coinvolgenti quantità non reali.

Equazioni di grado superiore… l l l La formula risolutiva delle equazioni di quarto grado fu scoperta da Ludovico Ferrari (1522 -1565). Anche queste formule furono pubblicate nell’Ars Magna e Cardano attribuisce a Ferrari il metodo. Dopo Tartaglia e Cardano per quasi due secoli si studiarono le equazioni di 5° grado e di grado superiore, ma tutti i vari tentativi fallirono. Nel 1799, nella sua tesi di laurea, Gauss (Carl Friedrich Gauss, 1777 -1855) dette una prima dimostrazione del teorema fondamentale dell’algebra : Ogni equazione algebrica di grado n ha almeno una radice complessa, sia che i coefficienti siano reali o complessi. Partendo da questo risultato (e utilizzando il teorema di Ruffini) si dimostra che ogni polinomio a coefficienti complessi si scompone in un prodotto di n fattori alcuni dei quali sono eventualmente ripetuti. Tuttavia, dopo i lavori di Gauss, rimaneva ancora aperta la questione se era possibile risolvere “per radicali” le equazioni algebriche di grado superiore al quarto. La risposta venne data da Paolo Ruffini (1765 -1822) e da Niels H. Abel (1802 -1829) in uno dei più celebri teoremi della matematica (teorema di Ruffini-Abel): per n>4 non si può fornire, in generale, una formula risolutiva per radicali delle equazioni algebriche.

Numeri complessi nella rivoluzione scientifica • Cartesio respinge le radici complesse scrivendo “Né le vere né le false radici sono sempre reali, talvolta esse sono immaginarie” • Newton non le considera significative e dice “Ma è giusto che le radici delle equazioni debbano essere spesso impossibili, per timore che esse debbano esibire i casi di problemi che sono impossibili come se fossero possibili” • Leibniz non ha idee chiare e afferma “Lo Spirito Divino trovò una via d’uscita in quel mostro dell’analisi, quel portento del mondo ideale, quell’anfibio fra essere e non-essere chiamiamo radice immaginaria dell’unità negativa”.
 Numeri immaginari storia
Numeri immaginari storia Numeri complessi da forma algebrica a esponenziale
Numeri complessi da forma algebrica a esponenziale Numeri indice
Numeri indice Numeri complessi zanichelli
Numeri complessi zanichelli Linea dei numeri relativi
Linea dei numeri relativi Semiretta graduata con numeri decimali
Semiretta graduata con numeri decimali Frazioni decimali
Frazioni decimali Equazione bisettrice
Equazione bisettrice Rette parallele e posizione reciproca di due rette
Rette parallele e posizione reciproca di due rette Mappa concettuale piano cartesiano e retta
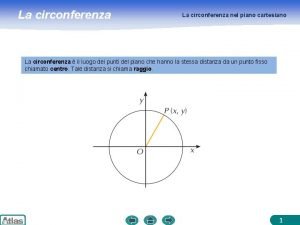
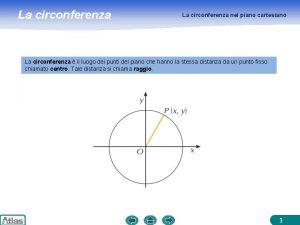
Mappa concettuale piano cartesiano e retta Circonferenza nel piano cartesiano
Circonferenza nel piano cartesiano Mappa rette parallele e perpendicolari
Mappa rette parallele e perpendicolari Disegna nel piano quadrettato un rettangolo
Disegna nel piano quadrettato un rettangolo Velocità tangenziale nel moto circolare uniforme
Velocità tangenziale nel moto circolare uniforme Trasformazione involutoria esempio
Trasformazione involutoria esempio Formula cerchio piano cartesiano
Formula cerchio piano cartesiano Terassendynamiek
Terassendynamiek Variazioni finanziarie attive e passive
Variazioni finanziarie attive e passive Variazioni ortografiche present continuous
Variazioni ortografiche present continuous Variazioni unilaterali del contratto tiscali
Variazioni unilaterali del contratto tiscali Riclassificazione stato patrimoniale
Riclassificazione stato patrimoniale Rendiconto finanziario arp
Rendiconto finanziario arp Complessi sopramolecolari
Complessi sopramolecolari I glucidi sono detti anche
I glucidi sono detti anche Lipidi semplici e complessi
Lipidi semplici e complessi Fosfolipidi
Fosfolipidi I sette gruppi alimentari
I sette gruppi alimentari Lipidi semplici e complessi
Lipidi semplici e complessi Disaccaridi
Disaccaridi Lipidi semplici
Lipidi semplici Costante di formazione kf
Costante di formazione kf Fisica dei sistemi complessi cos'è
Fisica dei sistemi complessi cos'è Bisogni comunicativi complessi
Bisogni comunicativi complessi Biomolecole mappa concettuale
Biomolecole mappa concettuale Aurelliac
Aurelliac Concetto di numero
Concetto di numero Diagramma di flusso scuola primaria
Diagramma di flusso scuola primaria Numeri iperreali
Numeri iperreali Quanti sono i numeri quantici
Quanti sono i numeri quantici Due numeri interi opposti hanno lo stesso valore assoluto
Due numeri interi opposti hanno lo stesso valore assoluto Cosa sono le proiezioni in geometria
Cosa sono le proiezioni in geometria Il nostro sistema è decimale perchè
Il nostro sistema è decimale perchè Filastrocca del pi greco
Filastrocca del pi greco El alfabeto en italiano
El alfabeto en italiano Parallelepipedo formule
Parallelepipedo formule Numero fisso trapezio isoscele
Numero fisso trapezio isoscele I numeri primi
I numeri primi Addizioni e sottrazioni con i numeri decimali
Addizioni e sottrazioni con i numeri decimali Divisibili per 3
Divisibili per 3 Tavola numeri casuali
Tavola numeri casuali Ah fisica
Ah fisica Numeri concordi e discordi
Numeri concordi e discordi Numeri geometrici
Numeri geometrici Idruri
Idruri Numeri figurati scuola primaria
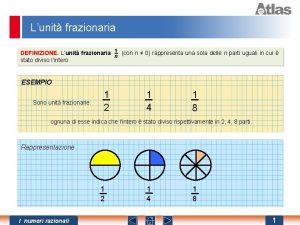
Numeri figurati scuola primaria Unità frazionaria esempi
Unità frazionaria esempi Un soggetto abituato a bere un quarto di vino al giorno
Un soggetto abituato a bere un quarto di vino al giorno Frazioni complementari
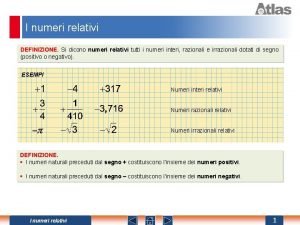
Frazioni complementari Numeri relativi
Numeri relativi Numeri divisibili per 100
Numeri divisibili per 100 Simbologia dei numeri nella divina commedia
Simbologia dei numeri nella divina commedia Perché i numeri naturali sono infiniti
Perché i numeri naturali sono infiniti Chimica nomenclatura tradizionale
Chimica nomenclatura tradizionale Numeri cardinali in inglese
Numeri cardinali in inglese Uk numeri decimali
Uk numeri decimali Valore relativo dei numeri naturali
Valore relativo dei numeri naturali