fine Questioni sullINFINITO I numeri naturali sono infiniti

fine Questioni sull’INFINITO

I numeri naturali sono infiniti. Anche i numeri razionali sono infiniti. … e in un segmento? Beh, allora, se parliamo d’infinito, in una retta ci sono infiniti punti

fine Attenzione. L’infinito é un campo Quando si parla dell’infinito in cui si deve entrare con precauzione. in matematica Molti matematici e filosofi hanno occorre fare attenzione. Leggiamo che cosa ne pensava disquisito su questo soggetto. Galileo Galilei

fine Discorsi e dimostrazioni matematiche, Giornata Prima (1638) Simplicio Salviati Qui nasce subito il dubbio, che mi pare insolubile: ed è, che sendo noi sicuri trovarsi linee una maggior dell'altra, tutta volta che amendue contenghino punti infiniti bisogna confessare trovarsi nel medesimo genere una cosa maggior dell'infinito, perché la infinità de i punti della linea maggiore eccederà l'infinità de i punti della minore. Ora questo darsi un infinito maggior dell'infinito mi par concetto da non poter esser capito in verun modo.

fine Discorsi e dimostrazioni matematiche, Giornata Prima (1638) Simplicio E u c li d e Salviati Qui nasce subito il dubbio, che mi pare insolubile: ed è, che sendo noi sicuri trovarsi linee una maggior dell'altra, tutta volta che amendue contenghino punti infiniti bisogna confessare trovarsi nel medesimo genere una cosa maggior dell'infinito, perché la infinità de i punti della linea maggiore eccederà l'infinità de i punti della minore. Ora questo darsi un infinito maggior dell'infinito mi par concetto da non poter esser capito in verun modo.

fine Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno a gl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente, perché stimo che questi attributi di maggioranza, minorità ed egualità non convenghino a gl'infiniti, de i quali non si può dire, uno esser maggiore o minore o eguale all'altro. (…) Discutendo su quanti sono i quadrati e le radici, rispetto a tutti i numeri

fine Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno a gl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente, perché stimo che questi attributi di maggioranza, minorità ed egualità non convenghino a gl'infiniti, de i quali non si può dire, uno esser maggiore o minore o eguale all'altro. (…) Discutendo su quanti sono i quadrati e le radici, rispetto a tutti i numeri

fine Ma se io domanderò, quante siano le radici, non si può negare che elle non siano quante tutti i numeri, (…) e pur da principio dicemmo, tutti i numeri esser assai più che tutti i quadrati, essendo la maggior parte non quadrati. (…) e pur nel numero infinito, se concepir lo potessimo, bisognerebbe dire, tanti essere i quadrati quanti tutti i numeri insieme.

fine Ma se io domanderò, quante siano le radici, non si può negare che elle non siano quante tutti i numeri, (…) e pur da principio dicemmo, tutti i numeri esser assai più che tutti i quadrati, essendo la maggior parte non quadrati. (…) e pur nel numero infinito, se concepir lo potessimo, bisognerebbe dire, tanti essere i quadrati quanti tutti i numeri insieme.

fine Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti i quadrati, infinite le loro radici, (…) E però quando il Sig. Simplicio mi propone più linee diseguali, e mi domanda come possa essere che nelle maggiori non siano più punti che nelle minori, io gli rispondo che non ve ne sono né più né manco né altrettanti, ma in ciascheduna infiniti.

fine Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti i quadrati, infinite le loro radici, (…) E però quando il Sig. Simplicio mi propone più linee diseguali, e mi domanda come possa essere che nelle maggiori non siano più punti che nelle minori, io gli rispondo che non ve ne sono né più né manco né altrettanti, ma in ciascheduna infiniti.

fine Ma cos’é l’infinito in matematica? Il tutto uguale ad una parte? I quadrati sono tanti quanti i numeri?

fine Sono stato io, Dedekind, a fine ottocento a fornire la definizione di infinito … … era necessario dar una definizione per evitare i paradossi Richard Dedekind

fine Un insieme S si dice infinito se é equipotente a una sua parte propria, altrimenti si dice finito equipotente Richard Dedekind

fine riprendiamo il discorso di … e costruiamo una Salviati « tanti essere i quadrati corrispondenza biunivoca tra quanti i numeri insieme » e questi due insiemi … cerchiamo di capire cosa intendeva esprimere … con « i numeri insieme » si riferiva ai numeri naturali consideriamo allora l’insieme dei numeri naturali N e l’insieme dei qudrati dei numeri naturali, QUAD Richard Dedekind

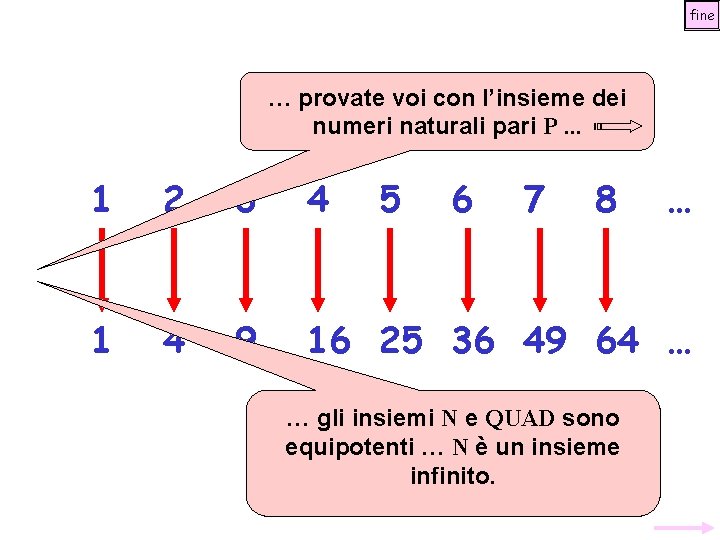
fine … provate voi con l’insieme dei numeri naturali pari P. . . 1 2 3 4 5 6 7 8 1 4 9 16 25 36 49 64 … … gli insiemi N e QUAD sono equipotenti … N è un insieme infinito. …

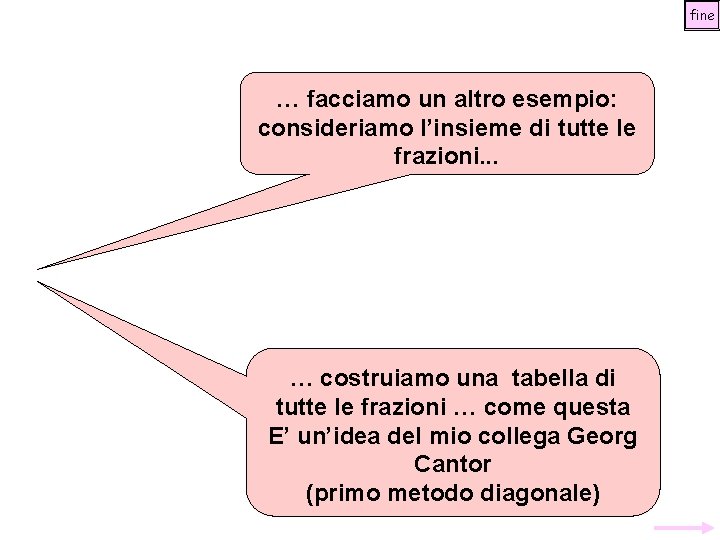
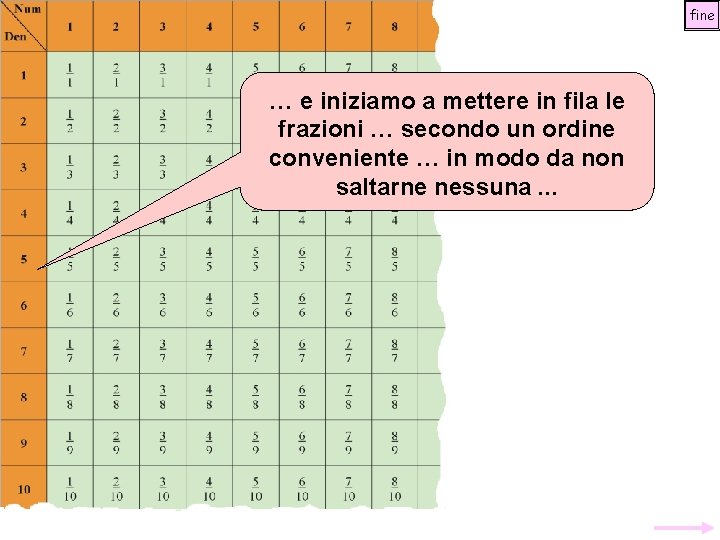
fine … facciamo un altro esempio: consideriamo l’insieme di tutte le frazioni. . . … costruiamo una tabella di tutte le frazioni … come questa E’ un’idea del mio collega Georg Cantor (primo metodo diagonale)

fine … e iniziamo a mettere in fila le frazioni … secondo un ordine conveniente … in modo da non saltarne nessuna. . .

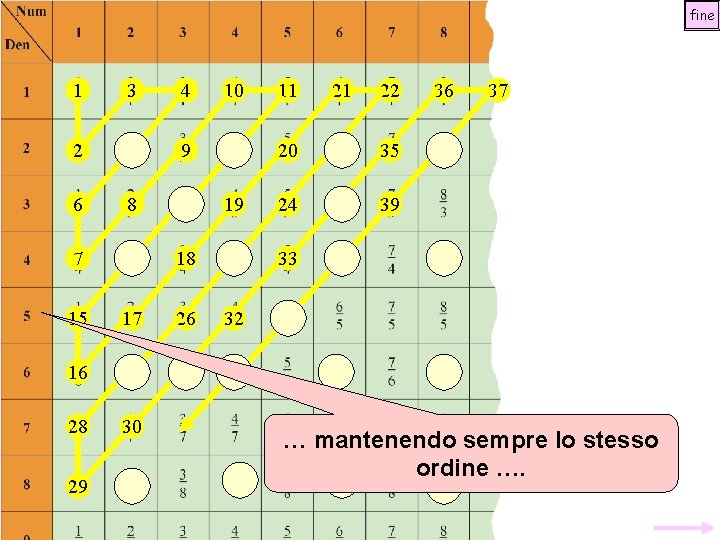
fine 1 3 4 10 11 21 22 36 2 5 9 12 20 23 35 38 6 8 13 19 24 34 39 7 14 18 25 15 17 26 32 16 27 31 42 28 30 29 37 Ogni volta che ritroviamo una 33 40 frazione ‘ equivalente ’ ad una già considerata, la saltiamo. 41 Così, saltiamo 2 ; 4 ; 3 ; 2 ; eccetera 2 2 3 4 …………. .

fine 1 3 4 10 11 21 22 36 2 5 9 12 20 23 35 38 6 8 13 19 24 34 39 7 14 18 25 33 40 15 17 26 32 41 16 27 31 42 28 30 29 37 … mantenendo sempre lo stesso ordine ….

fine 11 33 44 22 5 89 56 78 13 67 14 1418 11 15 12 16 1620 23 2635 15 19 19 24 34 2939 25 2533 40 13 17 20 26 24 32 41 27 21 28 23 30 22 29 910 1011 1721 1822 2736 31 12 42 38 28 37

fine 11 33 44 1620 23 2635 15 19 19 24 34 2939 25 2533 40 13 17 20 26 24 32 41 22 5 89 56 78 13 67 14 1418 11 15 12 16 27 21 28 23 30 22 29 910 1011 1721 1822 2736 31 12 3 28 37 4 38 42 Le frazioni sono quindi ordinate così.

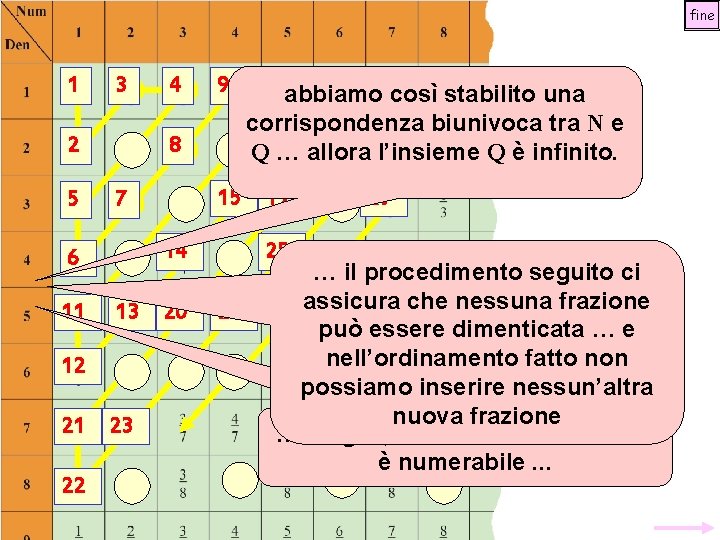
fine 11 33 44 22 5 89 56 78 13 67 14 1418 11 15 12 16 15 19 19 24 34 2533 40 25 13 17 20 26 24 32 27 21 28 23 30 22 29 1721 1822 2736 28 910 1011 37 abbiamo così stabilito una corrispondenza biunivoca tra N e 1620 23 2635 38 12 Q … allora l’insieme Q è infinito. 31 42 2939 … il procedimento seguito ci assicura che nessuna frazione 41 può essere dimenticata … e nell’ordinamento fatto non possiamo inserire nessun’altra nuova frazione … meglio, l’insieme delle frazioni è numerabile. . .

Attenzione: Naturalmente l’ordine in cui sono scritte le frazioni è un ordine convenzionale! non è il consueto ordinamento espresso dalla relazione ‘minore di’ <

La possibilità di stabilire una corrispondenza biunivoca tra N e Q può sembrare paradossale. Infatti, date in Q due frazioni a/b < c/d Posso sempre trovare una frazione compresa tra esse. Si può dimostrare facilmente che: a/b < (a+c)/(b+d) < c/d Questa proprietà si esprime dicendo che l’insieme Q dei razionali è denso. Questa proprietà è ovviamente falsa per l’insieme N dei naturali: quale naturale posso inserire tra 2 e 3?

fine Allora tutti gli insiemi infiniti sono equipotenti a N?

fine la situazione è un po ’ più complessa. . . Esistono insiemi infiniti non equipotenti Georg Cantor ho dimostrato che l’insieme N e l’insieme dei numeri reali compresi tra 0 e 1 non sono equipotenti Vediamo questo metodo (secondo metodo diagonale)

fine 0, 0, Ciascuno di voi mi detterà 0, un numero decimale 0, compreso tra zero e uno. 0,

fine 0, Scriverò le prime dieci 0, Ciascuno di voi mi detterà cifre, ma voi pensate 0, un numero decimale di andare 0, compreso tra zero e uno. avanti quanto volete. 0,

0, 0, 0, fine 0, 4412034567…. .

0, 4412034567…. . 0, 0, 2650134210…. . 0, fine

0, 4412034567…. . 0, 2650134210…. . 0, 0, 0, 1342500049…. 0, fine

0, 4412034567…. . 0, 2650134210…. . 0, 1342500049…. 0, 0, 0, 4444555320… fine

0, 4412034567…. . 0, 2650134210…. . 0, 1342500049…. 0, 4444555320… 0, 0, 1234567890. . . 0, 4444555320… fine

0, 4412034567…. . 0, 2650134210…. . 0, 1342500049…. 0, 4444555320… 0, 1234567890. . . fine

fine 0, 4412034567…. . Ammettiamo ora di 0, 2650134210…. . Ora, con il vostro aiuto, avere scritto in questo modo Eccetera …. . . 0, 1342500049…. scriverò un numero tutti i numeri decimali che sicuramente sfugge infiniti (compresi tra 0 e 1)in un certo 0, 4444555320… a questo ordinamento. ordine, scelto da voi. 0, 1234567890. . .

0, 3 5 3 3 0, 4412034567…. . ho scritto in blu 0, 2650134210…. . una cifra diversa 0, 1342500049…. da quella indicata 0, 4444555320… in rosso nella stessa 4…. 0, 1234567890. . . riga fine

0, 4412034567…. . Il numero scritto 0, 2650134210…. . in blu 0, 1342500049…. non compare tra quelli 0, 4444555320… che mi avete dettato. 0, 1234567890. . . Perché? 0, 35334… fine

0, 4412034567…. . 0, 2650134210…. . 0, 1342500049…. 0, 4444555320… 0, 1234567890. . . 0, 35334… fine E’ chiaro? Perché ha la prima cifra diversa da quella del primo numero; la seconda diversa da quella del secondo; la terza diversa da quella del terzo; eccetera ….

0, 4412034567…. . Qualunque sia l’ordine in cui 0, 2650134210…. . voi dettate i numeri, 0, 1342500049…. potrò sempre – in questo modo – 0, 4444555320… trovarne 0, 1234567890. . . uno che “sfugge” al 0, 35334… vostro elenco. fine

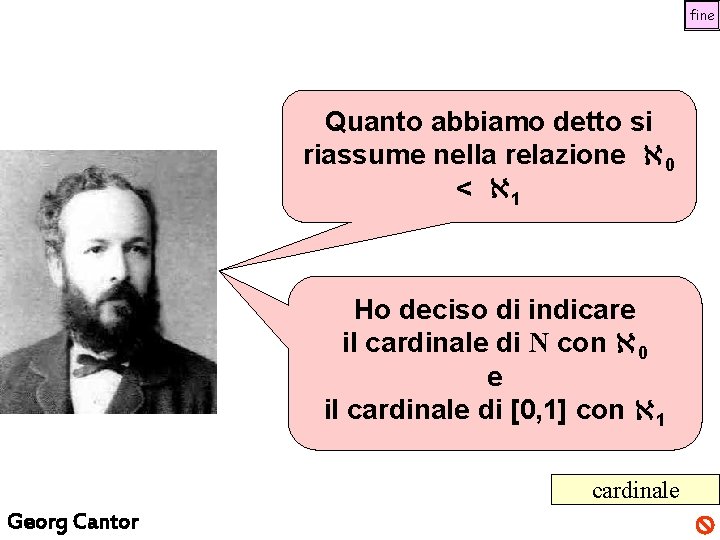
fine Quanto abbiamo detto si riassume nella relazione 0 < 1 Ho deciso di indicare il cardinale di N con 0 e il cardinale di [0, 1] con 1 cardinale Georg Cantor

Discorsi e dimostrazioni matematiche, Giornata Prima Qui nasce subito il dubbio, che mi pare insolubile: ed è, che sendo noi sicuri trovarsi linee una maggior dell'altra, tutta volta che amendue contenghino punti infiniti bisogna confessare trovarsi nel medesimo genere una cosa maggior dell'infinito, perché la infinità de i punti della linea maggiore eccederà la infinità de i punti della minore. Ora questo darsi un infinito maggior dell'infinito mi par concetto da non poter esser capito in verun modo. Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno agl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente, perché stimo che questi attributi di maggioranza, minorità ed egualità non convenghino a gl'infiniti, de i quali non si può dire, uno esser maggiore o minore o eguale all'altro. Per prova di che già mi sovvenne un sì fatto discorso, il quale per più chiara esplicazione proporrò per interrogazioni al Sig. Simplicio, che ha mossa la difficoltà. Io suppongo che voi benissimo sappiate quali sono i numeri quadrati, e quali i non quadrati.

Discorsi e dimostrazioni matematiche, Giornata Prima So benissimo che il numero quadrato è quello che nasce dalla moltiplicazione d'un altro numero in sé medesimo: e così il quattro, il nove, etc. , son numeri quadrati, nascendo quello dal dua, e questo dal tre, in sé medesimi moltiplicati Benissimo: e sapete ancora, che sì come i prodotti si dimandano quadrati, i producenti, cioè quelli che si multiplicano, si chiamano lati o radici; gli altri poi, che non nascono da numeri multiplicati in sé stessi, non sono altrimenti quadrati. Onde se io ti dirò, i numeri tutti, comprendendo i quadrati e i non quadrati, esser più che i quadrati soli, dirò proposizione verissima: non è così? Non si può dir altrimenti. Interrogando io di poi, quanti siano i numeri quadrati, si può con verità rispondere, loro esser tanti quante sono le proprie radici, avvenga che ogni quadrato ha la sua radice, ogni radice il suo quadrato, né quadrato alcuno ha più di una sola radice, né radice alcuna più d'un quadrato solo.

Discorsi e dimostrazioni matematiche, Giornata Prima Così sta. Ma se io domanderò, quante siano le radici, non si può negare che elle non siano quante tutti i numeri, poiché non vi è numero alcuno che non sia radice di qualche quadrato; e stante questo, converrà dire che i numeri quadrati siano quanti tutti i numeri, poiché tanti sono quante le lor radici, e radici sono tutti i numeri: e pur da principio dicemmo, tutti i numeri esser assai più che tutti i quadrati, essendo la maggior parte non quadrati. E pur tuttavia si va la moltitudine de i quadrati sempre con maggior proporzione diminuendo, quanto a maggior numeri si trapassa; perché sino a cento vi sono dieci quadrati, che è quanto a dire la decima parte esser quadrati; in dieci mila solo la centesima parte son quadrati, in un millione solo la millesima: e pur nel numero infinito, se concepir lo potessimo, bisognerebbe dire, tanti essere i quadrati quanti tutti i numeri insieme.

Discorsi e dimostrazioni matematiche, Giornata Prima Che dunque si ha da determinare in questa occasione? Sagredo Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti i quadrati, infinite le loro radici, né la moltitudine de' quadrati esser minore di quella di tutti i numeri, né questa maggior di quella, ed in ultima conclusione, gli attributi di eguale maggiore e minore non aver luogo ne gl'infiniti, ma solo nelle quantità terminate. E però quando il Sig. Simplicio mi propone più linee diseguali, e mi domanda come possa essere che nelle maggiori non siano più punti che nelle minori, io gli rispondo che non ve ne sono né più né manco né altrettanti, ma in ciascheduna infiniti. G. Galilei, Discorsi e dimostrazioni matematiche intorno a due nuove scienze.

Due insiemi M e N sono equipotenti se esiste una corrispondenza biunivoca di M in N

Quando due insiemi sono equipotenti, di dice che hanno lo stesso cardinale