I Numeri Naturali Presentazione e commenti a cura

I Numeri Naturali Presentazione e commenti a cura di LETIZIA LENTINI IIS SCIA FERMI CLASSE IB Anno Scolastico 2018/19 Liceo linguistico Prof. ssa R. DAMIANO Materia: MATEMATICA 1

• • • Definizione Rappresentazione Operazioni Addizione Moltiplicazione Sottrazione Divisione Potenza Espressioni 2

Definizione I numeri naturali sono i numeri che NATURALMENTE USIAMO PER CONTARE • Possiamo dare la seguente definizione: I Numeri Naturali sono TUTTI i numeri interi positivi a partire dallo zero: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … 3

4

5

Osservazioni • Si chiama successivo di un numero naturale quel numero che lo segue immediatamente nella successione naturale. Si chiama precedente di un numero naturale quel numero che lo precede. • Ogni numero naturale ammette un successivo, quindi, la successione naturale non finisce MAI, cioè L’INSIEME N DEI NUMERI NATURALI È INFINITO. • Ogni numero naturale ESCLUSO lo zero è successivo di un altro numero naturale. 6

Confronto in N 7

Dati due numeri naturali a e b : • Se occupano lo stesso posto nella successione naturale, allora sono uguali e si scrive a = b; • Se a precede b nella successione naturale allora a è minore di b e si scrive a < b; • Se a segue b nella successione naturale allora a è maggiore di b e si scrive a > b. 8

OPERAZIONI IN N • Nell’insieme dei numeri naturali si sono definite le quattro operazioni fondamentali: • ADDIZIONE • MOLTIPLICAZIONE • e le loro inverse, che sono, rispettivamente • SOTTRAZIONE • DIVISIONE. 9

Addizione Per addizionare due numeri naturali a e b, si devono sommare ad a tante unità quante sono quelle di b. Si otterrà un risultato c detto “somma” tra a e b. Quindi a+b=c dove a e b sono gli addendi, c è la somma e “+” il simbolo di addizione. Sulla semiretta orientata tale operazione si schematizza così: +b a c Si può notare come, assegnati due numeri naturali qualsiasi a e b, è sempre possibile ottenere c che è un numero naturale. Da ciò segue che l’addizione tra due numeri naturali è sempre possibile in N, cioè che N è un insieme chiuso rispetto all’addizione.

Le proprietà dell’addizione • Proprietà commutativa • Proprietà associativa • Proprietà dissociativa • Esistenza dell’elemento neutro

comm utativa Proprietà co Cambiando l’ordine degli addendi, la somma non cambia: a+b=b+a Esempio: 5+3=3+5=8

Proprietà a ssociativa Se si sommano tra loro tre o più addendi, il risultato non cambia se a due o più di essi si sostituisce la loro somma. (a+b)+ c = a + (b+c) Esempio: (4 +5) +3 = 4 + (5 +3)

Esistenza dell’elemento neutro Lo zero è definito elemento neutro dell’addizione: se si considera qualsiasi numero naturale e lo si addiziona a zero, il risultato è il numero stesso. a+0=0+a=a Esempio: 5+0=0+5=5

• La moltiplicazione è un’ addizione in cui gli addendi sono tutti uguali • 3 x 4=3+3+3+3=12 • Pertanto, la moltiplicazione risulta una operazione diretta i cui termini si dicono fattori, “x” o “·” è il simbolo, il risultato è detto prodotto. • È sempre possibile effettuare la moltiplicazione in N essendo questa un’operazione diretta e costituendo un ampliamento dell’addizione. • Quindi l’insieme N è chiuso rispetto alla moltiplicazione. 15

Le proprietà della moltiplicazione • Proprietà commutativa • Proprietà associativa • Proprietà distributiva della moltiplicazione rispetto alla somma e rispetto alla differenza • Esistenza dell’elemento neutro • Lo zero e la legge dell’annullamento del prodotto

Proprietà commutativa Cambiando l’ordine dei fattori, il prodotto non cambia. a·b=b·a Esempio: 5· 3=3· 5=15

Proprietà associativa Se si moltiplicano tra loro tre o più fattori, il prodotto non cambia se a due di essi si sostituisce il loro prodotto (a·b)·c=a·(b·c) Esempio: (3· 5)· 2=3·(5· 2)=30

Proprietà distributiva della moltiplicazione rispetto all’addizione e alla sottrazione. Se si deve moltiplicare una somma di più addendi (o una differenza) per un fattore, si può moltiplicare ogni termine per il fattore e quindi sommare (o sottrarre) i prodotti ottenuti. (a+b)·c=a·c+b·c c · (a+b) =c·a+c·b (a-b)·c=a·c-b·c Esempio: (3+2)· 4=3· 4+2· 4 c · (a-b) =c·a-c·b 2 · (5 -4) =2· 5 -2· 4

Elemento neutro della moltiplicazione Se si moltiplica per uno, un qualsiasi numero, il risultato è il numero stesso. a· 1=1·a=a Esempio: 5· 1=1· 5=5 Quindi il numero 1 è l’elemento neutro della moltiplicazione.

LO ZERO E LA LEGGE DI ANNULLAMENTO DEL PRODOTTO Se si moltiplica un qualsiasi numero per zero, il risultato è zero. a· 0=0 Esempio: 3· 0=0 0· 3=0 Da ciò ne consegue che il prodotto di due fattori è zero se almeno uno di essi è zero (legge di annullamento del prodotto). Esempio: a· 6=0 soltanto se a=0 0·a=0 a·b=0 almeno uno dei due fattori deve essere uguale a zero: a=0 o b=0

• Sottrarre da un numero naturale a un altro numero naturale b, significa trovare se esiste, un terzo numero naturale d che sommato al secondo dia il primo. Cioè : a – b = d SE d + b = a dove a si chiama minuendo, b si chiama sottraendo e d è la differenza o risultato della sottrazione. • La sottrazione NON è una operazione interna in N dato che è possibile SOLO SE il minuendo è maggiore o uguale al sottraendo. 22

La proprietà della sottrazione • La differenza tra due numeri non cambia se si aggiunge (o sottrae) ad entrambi uno stesso numero, cioè: a-b = d (a+m) - (b+m) = d (a-m) - (b-m) = d naturalmente è fondamentale che il numero m non superi sia a che b. Esempio: 15 -5 = 10 (15+3)-(5+3) = 18 -8 =10 (15 -3)-(5 -3) = 12 -2 = 10 23

Dividere un numero naturale per un altro diverso da zero, significa trovare se Esiste un terzo numero naturale che moltiplicato per il secondo dia il primo. Cioè : a: b = q se qxb = a dove a si chiama dividendo b si chiama divisore e q è il quoziente o risultato della divisione. • La divisione NON è una operazione interna in N dato che è possibile SOLO SE il dividendo è multiplo del divisore. Anche la divisione come la sottrazione non ha elemento neutro. 24

Proprietà della divisione • Proprietà invariantiva • Lo zero nella divisione

Proprietà invariantiva Moltiplicando o dividendo per una quantità diversa da zero, entrambi i termini di una divisione, il risultato non cambia. a: b=c Esempio: (a·m): (b·m)=c m 0 (a: m): (b: m)=c m 0 40: 8=5 (40: 2): (8: 2)=5 oppure: (9· 2): (3· 2)=3

Lo zero nella divisione Consideriamo il caso generico a: b. Ne consegue che: se a, b 0 allora - se a 0 e b 0 allora a: b=c determinata 8: 2=4 - Se a 0 e b=0 allora a: 0=impossibile 5: 0= impossibile perché non troverò mai un numero che moltiplicato per zero dia a. - Se a=0 e b Se b=0 allora 0: 0=indeterminata 0: 0= indeterminata perché qualsiasi numero moltiplicato per zero dà zero da zero.

• Dato un numero naturale a ed un numero n>1, si chiama potenza ennesima di a, il prodotto di n fattori uguali ad a. a si chiama base, n si chiama esponente e si scrive an • an = a x a… ripetuto n volte • Esempio: 32=3· 3=9 28

Proprietà delle potenze • 1 - Il prodotto di due potenze con uguale base è una potenza con la stessa base e con esponente la somma degli esponenti. • an. am = a n+m 32. 33 = 3 2+3 =35 • 2 - Il quoziente di due potenze con uguale base è una potenza con la stessa base e con esponente la differenza degli esponenti. • an : am = a n-m 33 : 32 = 3 3 -2 =3 • 3 - La potenza di una potenza è una potenza con la stessa base e con esponente il prodotto degli esponenti. • (an)m = a n x m (32)3 = a 2 x 3 = 36 29

• 4 - Il prodotto di più potenze con uguale esponente è una potenza avente lo stesso esponente e come base il prodotto delle basi. • an. bn = (a. b) n 32. 22 = (3. 2) 2 • 5 - Il quoziente fra due potenze con uguale esponente è una potenza avente lo stesso esponente e come base il quoziente fra le due basi. • 62 : 22 = (6 : 2) 2 30

RIEPILOGANDO 31

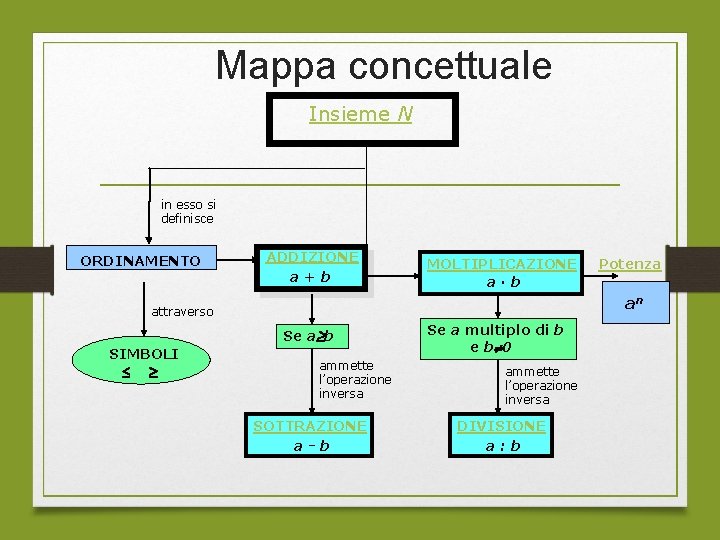
Mappa concettuale Insieme N in esso si definisce ORDINAMENTO ADDIZIONE a+b MOLTIPLICAZIONE a·b an attraverso Se a b SIMBOLI Potenza ammette l’operazione inversa SOTTRAZIONE a-b Se a multiplo di b e b 0 ammette l’operazione inversa DIVISIONE a: b

• Si chiama espressione aritmetica una sequenza finita di numeri e simboli (i segni delle operazioni e le parentesi). • Per risolvere le espressioni basta applicare le proprietà viste fino ad ora, tenendo presente che: • - se l’espressione non contiene parentesi, le moltiplicazioni e le divisioni si DEVONO eseguire prima delle addizioni e delle sottrazioni. • Es. 3 + 3· 2 - 4= 3 + 6 - 4 = 5 • - se l’espressione contiene parentesi bisogna risolvere le operazioni che compaiono nelle parentesi più interne e procedere poi verso l’esterno. • Es. {9 • 9 – [8 + 5]} : {[37 – 35] • 2} ={9 • 9 – 13} : {2 • 2} ={81 – 13} : 4 = 68 : 4 = 17 33