Curiosit su numeri naturali consecutivi come ottenere serie

Curiosità su numeri naturali consecutivi come ottenere serie di quadrati, cubi, quarte potenze senza moltiplicazioni numeri figurati quadrati, triangolari, tetraedrici fattoriali tavola pitagorica

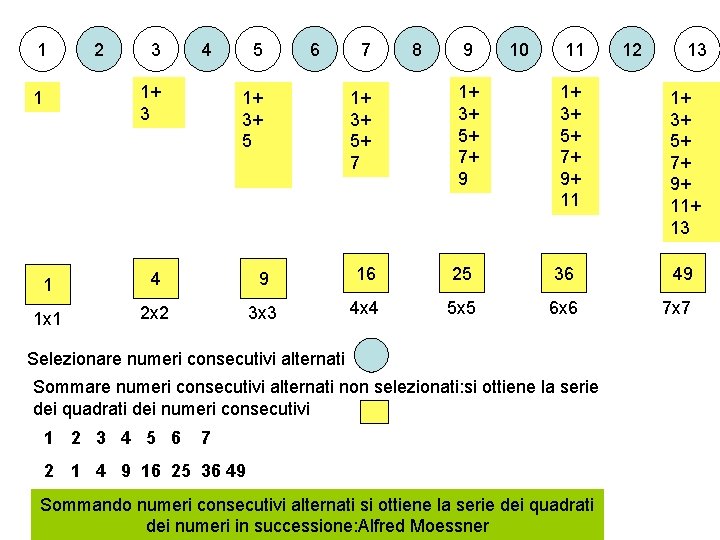
1 2 3 4 1+ 3 1 5 6 1+ 3+ 5 7 1+ 3+ 5+ 7 8 9 1+ 3+ 5+ 7+ 9 10 11 1+ 3+ 5+ 7+ 9+ 11 12 13 1+ 3+ 5+ 7+ 9+ 11+ 13 1 4 9 16 25 36 49 1 x 1 2 x 2 3 x 3 4 x 4 5 x 5 6 x 6 7 x 7 Selezionare numeri consecutivi alternati Sommare numeri consecutivi alternati non selezionati: si ottiene la serie dei quadrati dei numeri consecutivi 1 2 3 4 5 6 7 2 1 4 9 16 25 36 49 Sommando numeri consecutivi alternati si ottiene la serie dei quadrati dei numeri in successione: Alfred Moessner

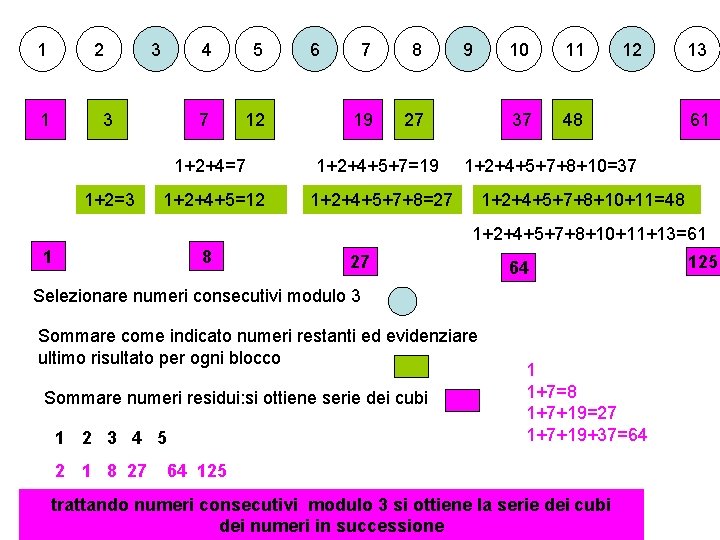
1 2 1 3 3 1+2=3 4 5 7 12 6 7 8 19 27 1+2+4=7 1+2+4+5+7=19 1+2+4+5=12 1+2+4+5+7+8=27 9 10 11 37 48 12 13 61 1+2+4+5+7+8+10=37 1+2+4+5+7+8+10+11=48 1+2+4+5+7+8+10+11+13=61 1 8 27 64 Selezionare numeri consecutivi modulo 3 Sommare come indicato numeri restanti ed evidenziare ultimo risultato per ogni blocco Sommare numeri residui: si ottiene serie dei cubi 1 2 3 4 5 2 1 8 27 1 1+7=8 1+7+19=27 1+7+19+37=64 64 125 trattando numeri consecutivi modulo 3 si ottiene la serie dei cubi dei numeri in successione 125

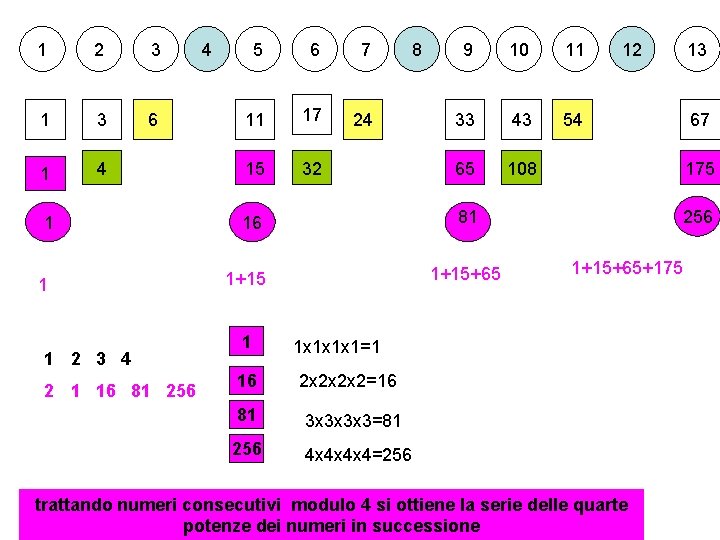
1 2 3 1 3 6 1 4 1 1 1 2 3 4 2 1 16 81 256 4 5 6 7 11 17 24 15 32 8 11 33 43 54 65 108 1+15+65 1+15 16 10 12 1+15+65+175 2 x 2 x 2 x 2=16 3 x 3 x 3 x 3=81 256 4 x 4 x 4 x 4=256 67 256 1 x 1 x 1 x 1=1 81 13 175 81 16 1 9 trattando numeri consecutivi modulo 4 si ottiene la serie delle quarte potenze dei numeri in successione

Numeri figurati rappresentabili con immagini geometriche bi-tridimensionali esempi quadrati triangolari tetraedrici pentagonali

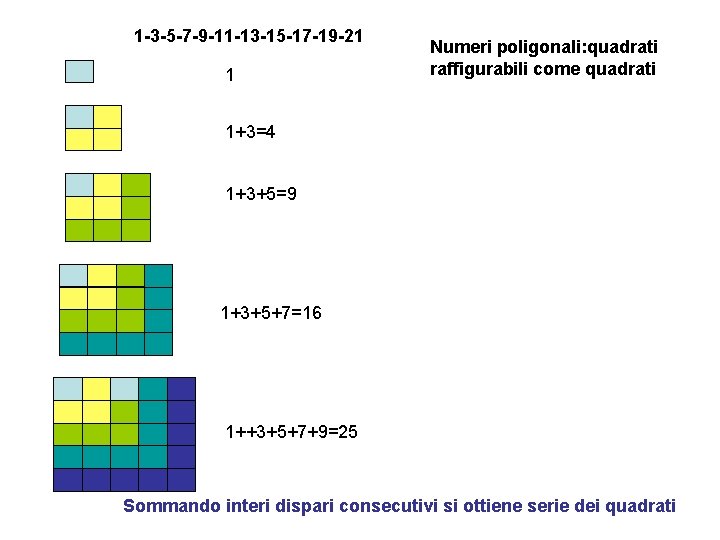
1 -3 -5 -7 -9 -11 -13 -15 -17 -19 -21 1 Numeri poligonali: quadrati raffigurabili come quadrati 1+3=4 1+3+5=9 1+3+5+7=16 1++3+5+7+9=25 Sommando interi dispari consecutivi si ottiene serie dei quadrati

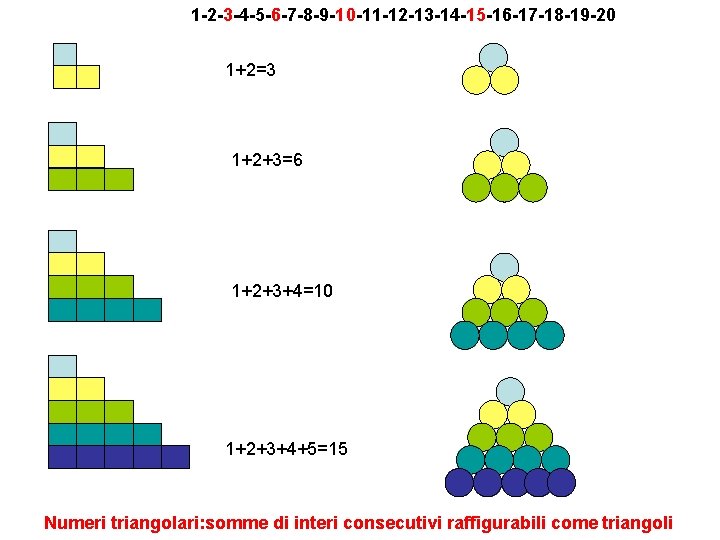
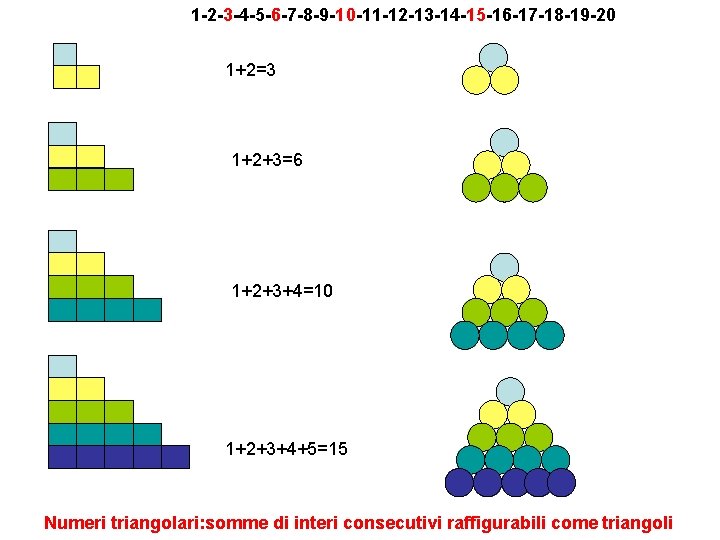
1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 -18 -19 -20 1+2=3 1+2+3=6 1+2+3+4=10 1+2+3+4+5=15 Numeri triangolari: somme di interi consecutivi raffigurabili come triangoli

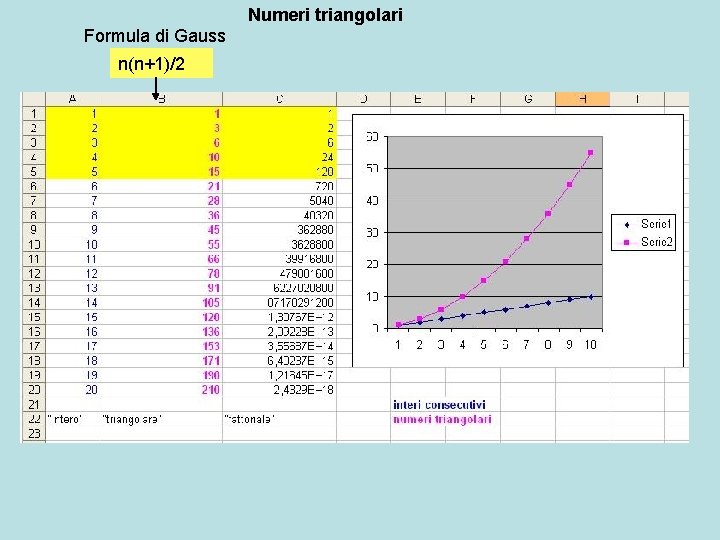
Numeri triangolari n(n+1)/2 Formula di Gauss 1 2+1=3 3+2+1=6 4+3+2+1=10 5+4+3+2+1=15 6+5+4+3+2+1=21 1! = 1 2! = 1 x 2 = 2 3! = 1 x 2 x 3 = 6 4! = 1 x 2 x 3 x 4 = 24 5! = 1 x 2 x 3 x 4 x 5 = 120 6! = 1 x 2 x 3 x 4 x 5 x 6 = 720 7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 5040 e numeri fattoriali ricavabili 1(1+1)/2=1 2(2+1)/2=3 3(3+1)/2=6 4(4+1)/2=10 5(5+1)/2=15 6(6+1)/2=21

Numeri triangolari Formula di Gauss n(n+1)/2

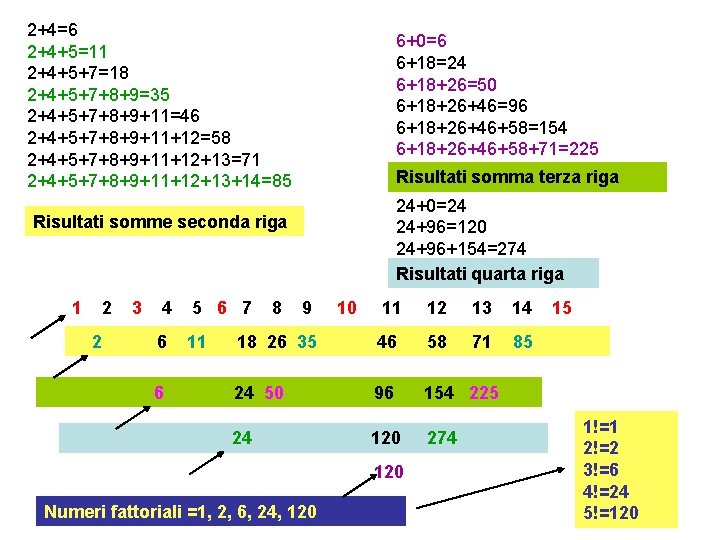
2+4=6 2+4+5=11 2+4+5+7=18 2+4+5+7+8+9=35 2+4+5+7+8+9+11=46 2+4+5+7+8+9+11+12=58 2+4+5+7+8+9+11+12+13=71 2+4+5+7+8+9+11+12+13+14=85 6+0=6 6+18=24 6+18+26=50 6+18+26+46=96 6+18+26+46+58=154 6+18+26+46+58+71=225 Risultati somma terza riga 24+0=24 24+96=120 24+96+154=274 Risultati quarta riga Risultati somme seconda riga 1 2 2 3 4 5 6 7 6 11 6 8 9 10 11 12 13 14 18 26 35 46 58 71 85 24 50 96 154 225 24 120 274 120 Numeri fattoriali =1, 2, 6, 24, 120 15 1!=1 2!=2 3!=6 4!=24 5!=120

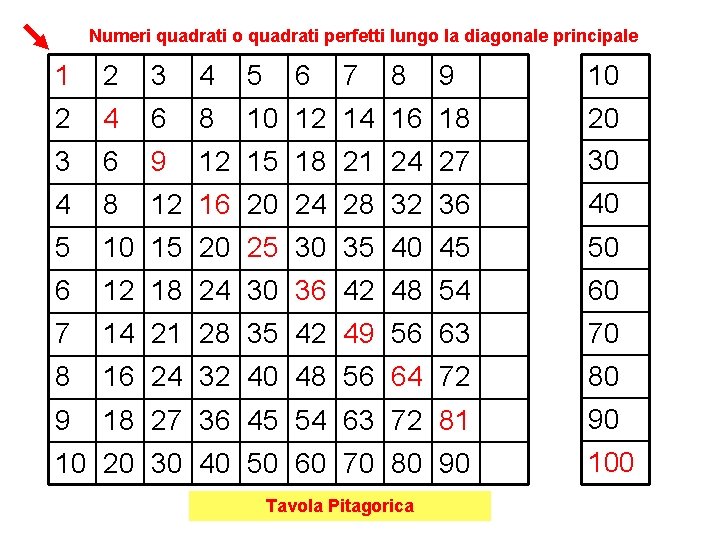
Numeri quadrati o quadrati perfetti lungo la diagonale principale 1 2 3 4 5 6 7 8 9 2 4 6 8 10 12 14 16 18 3 6 9 12 15 18 21 24 27 20 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 20 30 40 50 60 70 80 90 Tavola Pitagorica 10 100

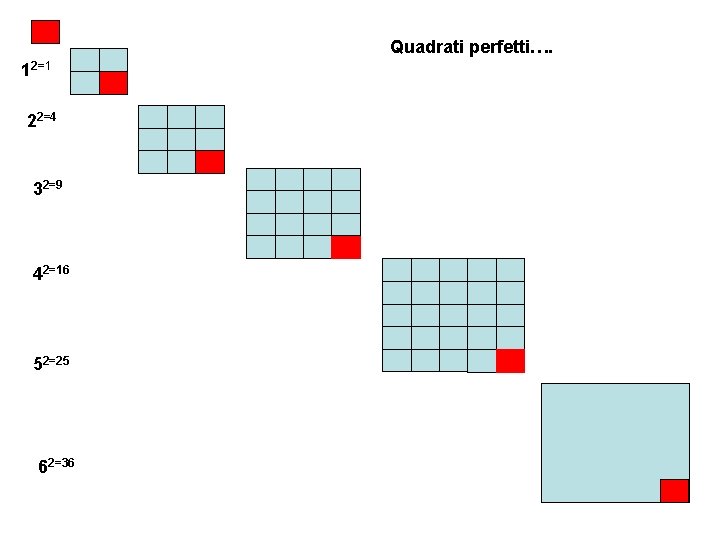
Quadrati perfetti…. 12=1 22=4 32=9 42=16 52=25 62=36

1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 -18 -19 -20 1+2=3 1+2+3=6 1+2+3+4=10 1+2+3+4+5=15 Numeri triangolari: somme di interi consecutivi raffigurabili come triangoli

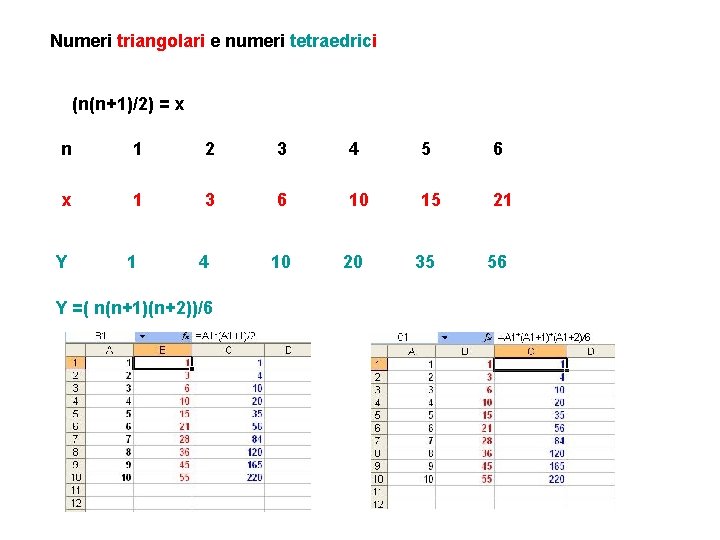
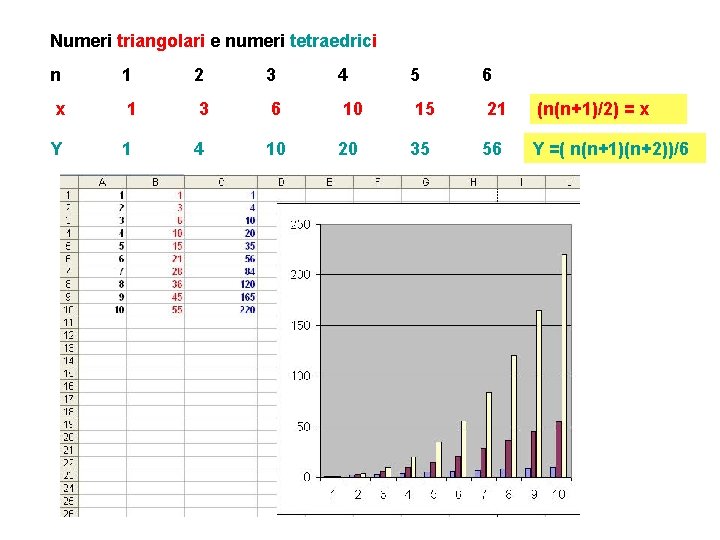
Numeri triangolari e numeri tetraedrici (n(n+1)/2) = x n 1 2 3 4 5 6 x 1 3 6 10 15 21 Y 1 4 Y =( n(n+1)(n+2))/6 10 20 35 56

Numeri triangolari e numeri tetraedrici n x Y 1 1 1 2 3 4 3 6 10 4 10 20 5 15 35 6 21 56 (n(n+1)/2) = x Y =( n(n+1)(n+2))/6

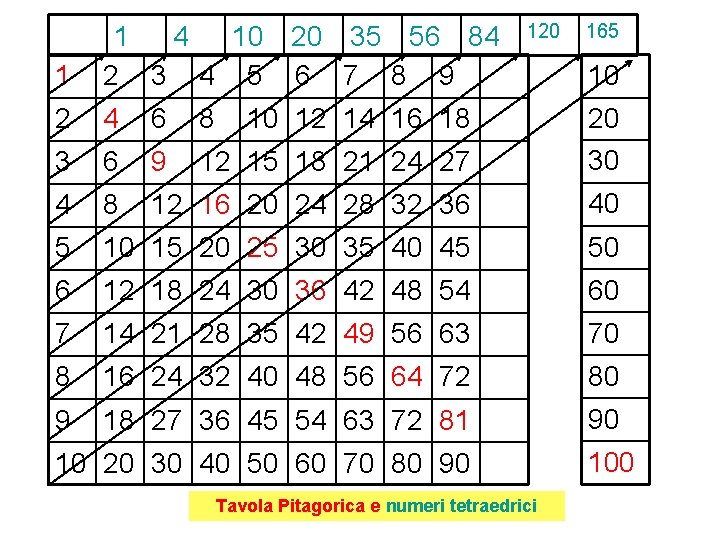
120 165 1 1 4 10 20 35 56 84 2 3 4 5 6 7 8 9 2 4 6 8 3 6 9 12 15 18 21 24 27 20 30 4 8 12 16 20 24 28 32 36 40 5 10 15 20 25 30 35 40 45 50 6 12 18 24 30 36 42 48 54 60 7 14 21 28 35 42 49 56 63 70 8 16 24 32 40 48 56 64 72 80 9 18 27 36 45 54 63 72 81 90 10 12 14 16 18 10 20 30 40 50 60 70 80 90 Tavola Pitagorica e numeri tetraedrici 10 100

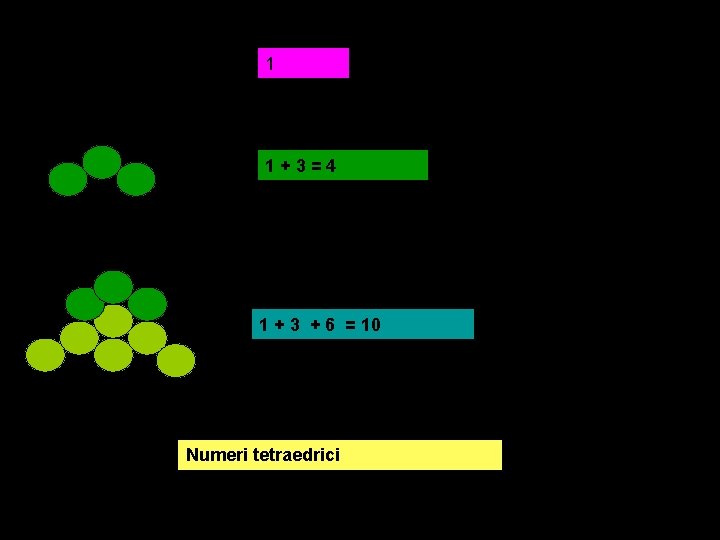
1 1+3=4 1 + 3 + 6 = 10 Numeri tetraedrici

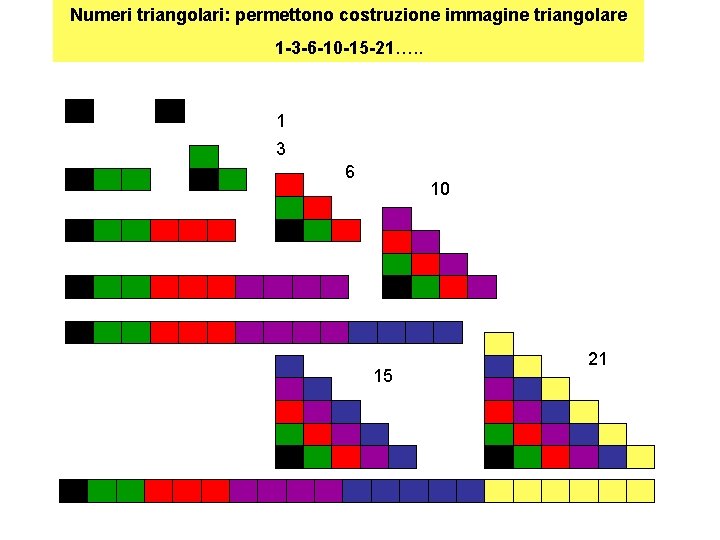
Numeri triangolari: permettono costruzione immagine triangolare 1 -3 -6 -10 -15 -21…. . 1 3 6 10 15 21

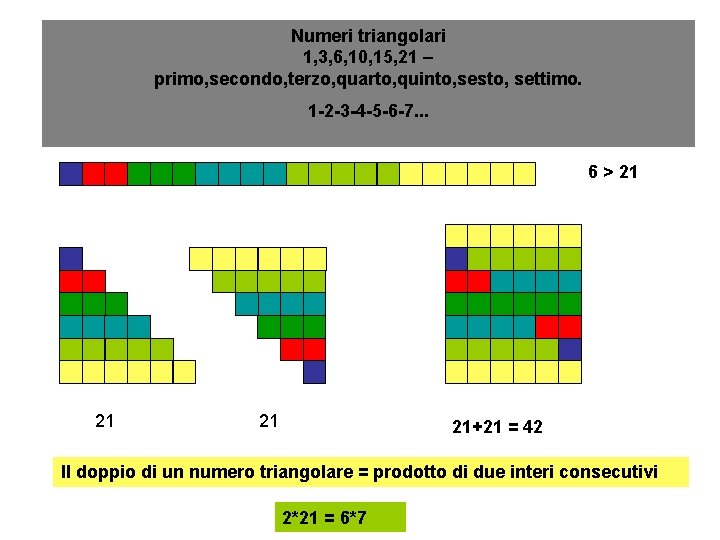
Numeri triangolari 1, 3, 6, 10, 15, 21 – primo, secondo, terzo, quarto, quinto, sesto, settimo. 1 -2 -3 -4 -5 -6 -7. . . 6 > 21 21+21 = 42 Il doppio di un numero triangolare = prodotto di due interi consecutivi 2*21 = 6*7

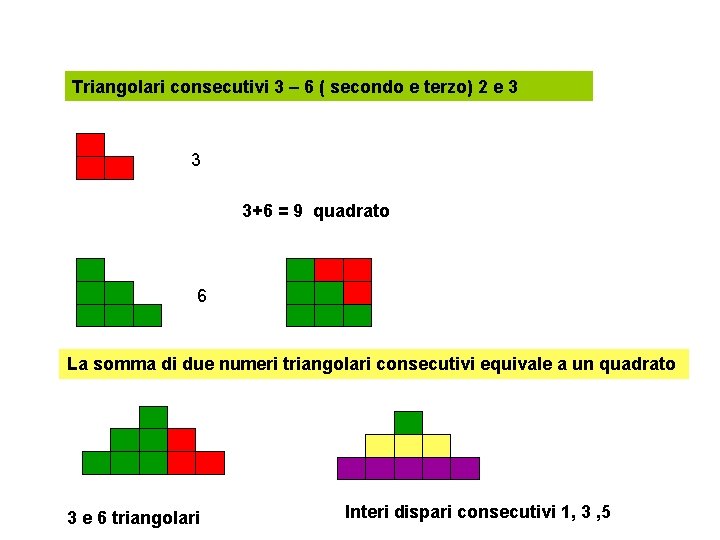
Triangolari consecutivi 3 – 6 ( secondo e terzo) 2 e 3 3 3+6 = 9 quadrato 6 La somma di due numeri triangolari consecutivi equivale a un quadrato 3 e 6 triangolari Interi dispari consecutivi 1, 3 , 5

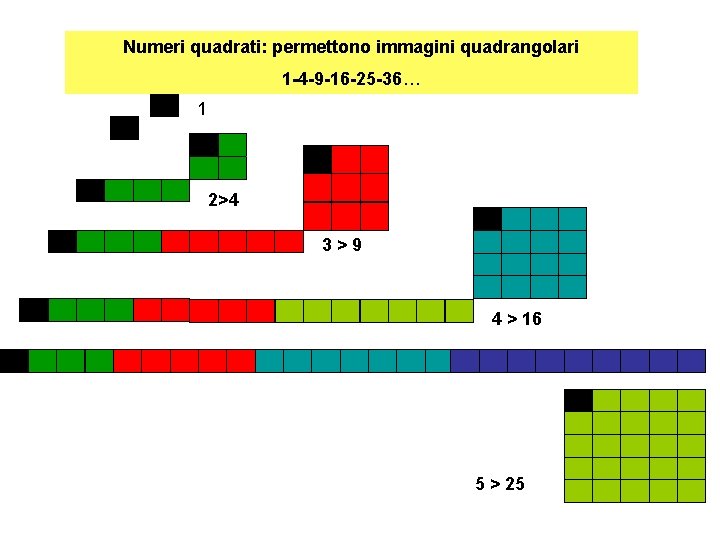
Numeri quadrati: permettono immagini quadrangolari 1 -4 -9 -16 -25 -36… 1 2>4 3>9 4 > 16 5 > 25

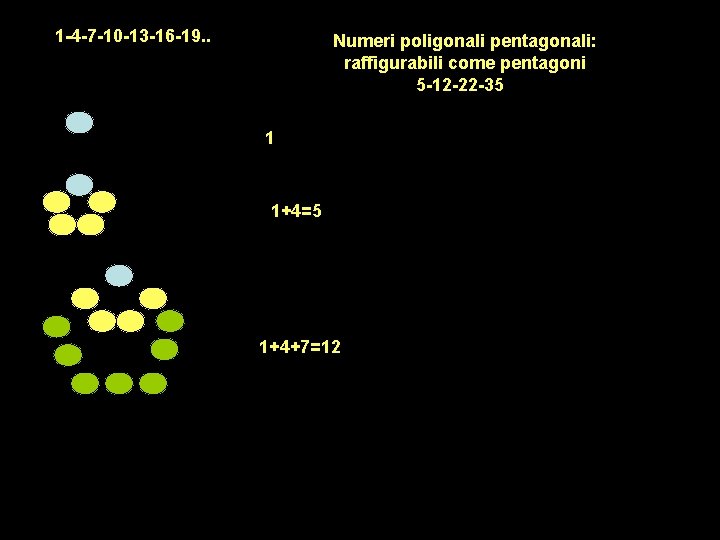
1 -4 -7 -10 -13 -16 -19. . Numeri poligonali pentagonali: raffigurabili come pentagoni 5 -12 -22 -35. . 1 1+4=5 1+4+7=12

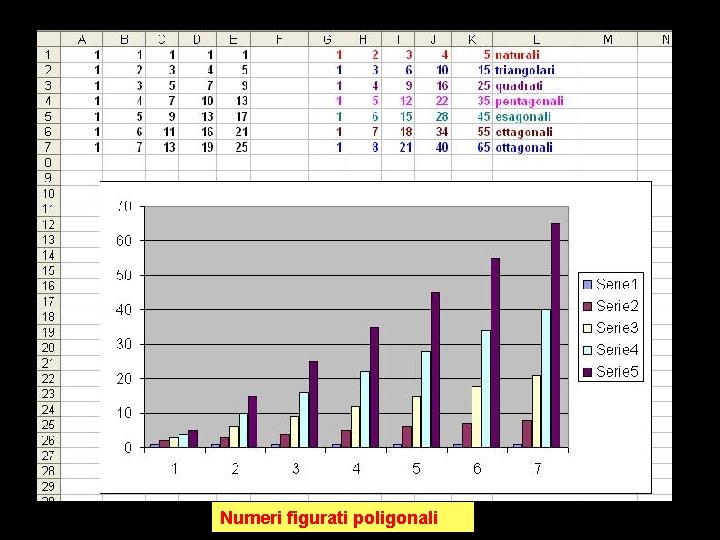
Numeri figurati poligonali

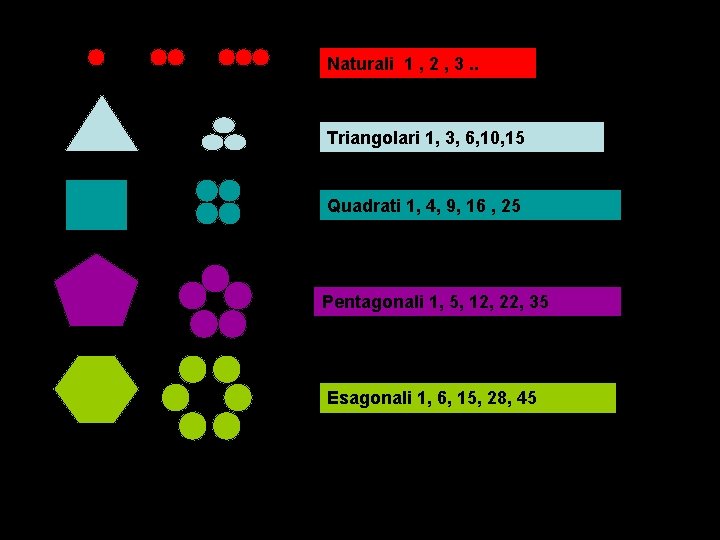
Naturali 1 , 2 , 3. . Triangolari 1, 3, 6, 10, 15 Quadrati 1, 4, 9, 16 , 25 Pentagonali 1, 5, 12, 22, 35 Esagonali 1, 6, 15, 28, 45