A spasso per la storia tra infiniti e

A spasso per la storia tra infiniti e infinitesimi

La storia del Calcolo Sublime Solo due grandi protagonisti? Newton e Leibniz… Leibniz e Newton… … O ANCHE ALTRI?

La storia “non sequenziale” del Calcolo Sublime Infiniti: paradosso di Interesse per processi infinitesimali (Anassagora) Metodo di esaustione (Eudosso, Archimede) Metodo degli indivisibili (Cavalieri) Achille e della tartaruga (Zenone) Metodi euristici (Archimede) Calcolo differenziale e integrale (Newton, Leibniz) Concezione assiomatica dei reali. Infinitesimo attuale (Robinson) La S. I. A. Infinito potenziale, serie (Aristotele) Serie non convergenti (Oresme, Grandi) Infinito attuale e cardinali transfiniti (Cantor)

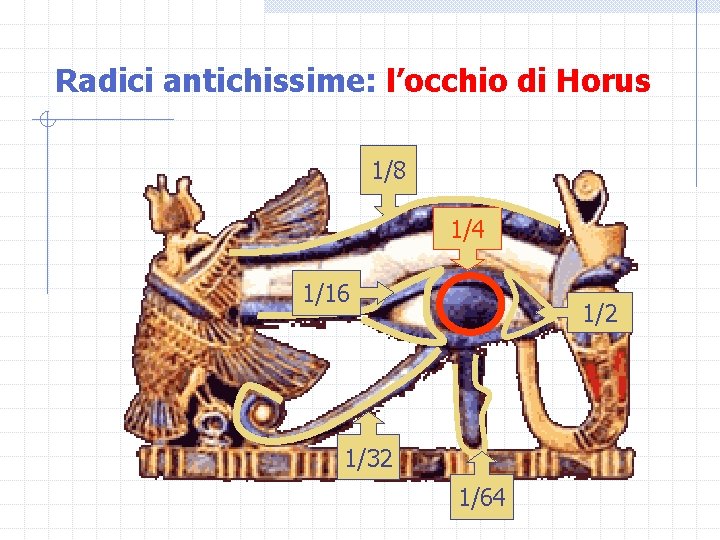
Radici antichissime: l’occhio di Horus 1/8 1/4 1/16 1/2 1/32 1/64

Gli Egiziani e le (prime) potenze di ½ (1/2) + (1/4) + (1/8) + (1/16) + (1/32) + (1/64) = 1! Il risultato esatto sarebbe: 63/64 (cioè: 1 – 1/64) È un primo abbozzo di procedimento “infinitesimale”, ma interrotto quando le quantità coinvolte diventano “troppo piccole” (minori di 1/64). Contesto culturale: tutto ciò è in perfetto accordo con lo spirito della matematica egizia, supporto per gli ingegneri più che ricerca teorica vera e propria.

Il mito dell’occhio di Horus consente una riflessione matematica Riprendiamo l’esempio… senza fermarci: ad una “addizione di infiniti addendi”, intuitivamente, è sempre associata una somma infinitiamente grande. Infatti se addizioniamo tutte le potenze di un numero positivo (ad esempio 2): 1+2+4+8+32+64+… superiamo ogni k>0, qualsiasi sia il k considerato. Ma se quel numero è invece minore di 1? 1+(1/2)+(1/4)+(1/8)+(1/16)+(1/32)+ +(1/64)+…

Riflettiamo sull’ultimo esempio 1+(1/2)+(1/4)+(1/8)+(1/32)+(1/64)+… supera ogni k>0, qualsiasi sia il k considerato? La risposta è no. Basta prendere k = 2 : la somma non supererà mai 2, qualsiasi sia il numero di addendi considerati: 1 : per arrivare a 2 dovremmo aggiungere 1; aggiungiamo la metà di ciò che manca: ½ 1+ ½ : per arrivare a 2 dovremmo aggiungere ½ aggiungiamo la metà di ciò che manca: ¼ … e via di seguito: aggiungiamo sempre la metà di ciò che manca… quindi non supereremo mai 2.

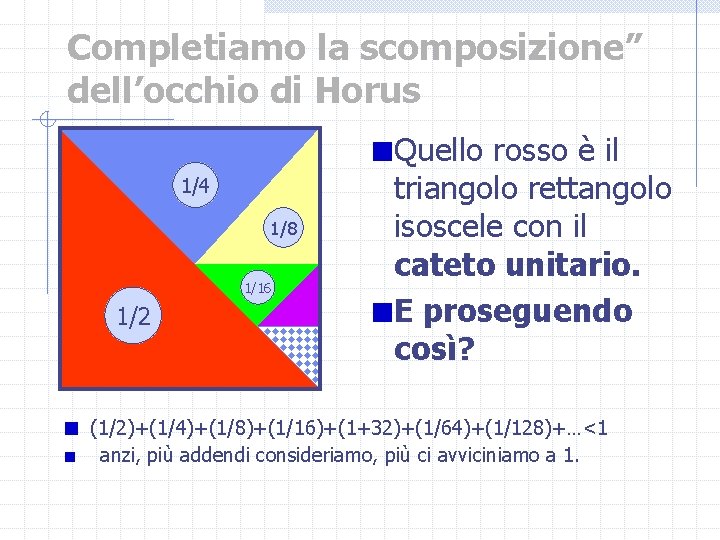
Completiamo la scomposizione” dell’occhio di Horus 1/4 1/8 1/16 1/2 Quello rosso è il triangolo rettangolo isoscele con il cateto unitario. E proseguendo così? (1/2)+(1/4)+(1/8)+(1/16)+(1+32)+(1/64)+(1/128)+…<1 anzi, più addendi consideriamo, più ci avviciniamo a 1.

Un altro antico esempio Per superare l’idea (errata!) “infiniti addendi, somma infinita” ci riferiremo a Zenone d’Elea (490 – 430 a. C. ) e al paradosso di Achille e della Tartaruga. una “addizione con infiniti addendi” la cui somma non supera, per quanti addendi si considerino, un numero finito. Riflettendo sulla rincorsa di Achille alla Tartaruga, infatti , calcoleremo la somma (finita) di tutte le (infinite) potenze di 1/10.

Zenone, Achille e la Tartaruga A. concede 1 m di vantaggio a T. ed è 10 volte più veloce di essa. Quando A. avrà raggiunto la posizione iniziale di T. , T. avrà percorso nuovamente 0, 1 m. Raggiunta poi questa seconda posizione, A. percorrerà dunque: 1+0, 001+… =1, 111… Dopo 1, 2 m Achille avrà superato Tartaruga! 1+1/100+1/1000+… =10/9 P. S. A Zenone (scuola eleatica) l’argomento serve per negare la realtà del moto.

Anassagora, e i suoi processi infinitesimali Nulla nasce e nulla perisce, ma nascita e morte sono solo termini convenzionalmente utilizzati dagli esseri umani per identificare mescolanza e disgregazione delle parti dell’Essere. Anassagora chiama queste parti semi originari. Anassagora di Clazomene, (496 a. C. – Lampsaco, 428 a. C. circa). Fu il primo filosofo a "importare" la filosofia nella penisola greca, più precisamente ad Atene (prima di lui la filosofia era diffusa solamente nelle colonie greche dell'Asia Minore e della Magna Grecia). I semi sono caratterizzati dall’essere di numero infinito, identici tra loro e infinitamente divisibili.

Eudosso, i numeri “reali” e il metodo di… Eudosso di Cnido (408 – 355 a. C. ) matematico e astronomo, cui sono attribuiti risultati fondamentali per il costituirsi della matematica come scienza. Secondo Archimede, Eudosso sviluppò la teoria delle proporzioni che consentì di superare le difficoltà che si incontrano per trattare i numeri irrazionali; questa teoria sarà ripresa negli Elementi di Euclide e in sostanza consente di trattare rigorosamente i numeri reali pensati come rapporti di grandezze. Eudosso sviluppò il metodo di esaustione di Antifone, che sarà usato in modo magistrale da Archimede e la dimostrazione rigorosa delle formule che forniscono i volumi del cono e della piramide.

Aristotele, e l’in-finito L' infinito è essere in potenza, ed è essere come potenza ed essere come atto. La caratteristica essenziale dell'infinito è proprio quella di essere non finito e dunque essere costantemente incompiuto. Quindi per l'infinito passare dalla potenza (la possibilità di realizzarsi come infinito) all’atto (quando questa possibilità si è realizzata) non comporta nessuna reale trasformazione o acquisizione di caratteristiche prima non aveva, come avviene comunemente nel passaggio dalla potenza all'atto. Infatti infinito era prima (essere come potenza) ed infinito è dopo (essere come atto).

Aristotele, e l’in-finito Condividendo la concezione pitagorica fondata su argomenti etico-estetici più che fisici, ma fondati logicamente, anche Aristotele concepisce l'idea che l'infinito è equivalente all'imperfezione perché mai compiuto, non pienamente realizzato, come è invece per il finito a cui non manca niente per essere completo.

Archimede, e i suoi processi di esaustione Nel breve lavoro La misura del cerchio viene dimostrato che un cerchio è equivalente a un triangolo con base eguale alla circonferenza e altezza eguale al raggio. Tale risultato è ottenuto approssimando arbitrariamente il cerchio, dall’interno e dall'esterno, con poligoni regolari inscritti e circoscritti. Con lo stesso procedimento Archimede espone un metodo con il quale può approssimare arbitrariamente il rapporto tra circonferenza e diametro di un cerchio dato, rapporto che oggi si indica con π. Le stime esplicitamente ottenute limitano questo valore fra 22/7 (circa 3. 1429) e 223/71 (circa 3. 1408). Archimede di Siracusa (circa 287 a. C. – 212 a. C. ) matematico, ingegnere, fisico e inventore siceliota. Uno dei massimi scienziati della storia. Qui sopra in un dipinto di Domenico Fetti (1620)

Archimede, e il metodo Il metodo (perduto almeno dal Medioevo, letto per la prima volta nel famoso palinsesto trovato da Heiberg nel 1906, poi perduto e ritrovato nel 1998) consente di penetrare nei procedimenti usati da Archimede nelle sue ricerche. Rivolgendosi ad Eratostene, spiega di usare due diversi metodi nel suo lavoro. Una volta individuato il risultato voluto, per dimostrarlo formalmente usava quello che poi fu chiamato “metodo di esaustione”, del quale si hanno molti esempi in altre sue opere. Tale metodo non forniva però una chiave per individuare i risultati. Il “metodo meccanico” è basato sulla sua statica e sull'idea di dividere le figure in un numero infinito di parti infinitesime. Archimede considerava questo secondo metodo non rigoroso ma, a vantaggio degli altri matematici, fornisce esempi del suo valore euristico nel trovare aree e volumi; ad esempio, il metodo meccanico è usato per individuare l’area di un segmento di parabola.

Archimede, e la prima serie Nell’opera Quadratura della parabola calcola l’area di un segmento di parabola. Si considerano le rette parallele all’asse della parabola passanti per gli estremi della base. Viene poi tracciata una terza retta parallela alle prime due e da loro equidistante. L’intersezione di quest’ultima retta con la parabola determina il terzo vertice del triangolo. Sottraendo al segmento di parabola il massimo triangolo inscritto si ottengono due nuovi segmenti di parabola, nei quali si possono inscrivere due nuovi triangoli. Iterando il procedimento si riempie il segmento di parabola con infiniti triangoli. L’area richiesta è ottenuta calcolando l’area di tutti i triangoli e sommando gli infiniti termini ottenuti. Il passo finale si riduce alla somma della serie geometrica di ragione 1/4: È questo il primo esempio conosciuto di somma di una serie. P. S. All’inizio dell'opera è introdotto quello che è ancora oggi chiamato assioma di Archimede.

Eudosso e Archimede Il lavoro di Eudosso e Archimede come precursori del calcolo infinitesimale, verrà superato in sofisticatezza e rigore matematico solo dal matematico indiano Bhaskara II (1114 -1185) e da Isaac Newton (1642 -1727).

Nicola d’Oresme, genio Inventa un metodo delle coordinate (300 anni prima di Cartesio)… … lo applica al movimento di un punto e trova la legge del moto (300 anni prima di Galileo) Sviluppa il primo metodo di calcolo delle potenze frazionarie, la applica ai rapporti musicali e inventa la scala temperata (250 anni prima di Simon Stevin) Si interessa alla somme infinite Nicole Oresme (1323 – 11 luglio 1382) fu matematico, fisico, astronomo e economista, vescovo, filosofo, psicologo e musicologo. Fu uno dei più famosi e influenti pensatori del tardo Medioevo; fu inoltre un teologo appassionato, traduttore competente, influente consigliere di re Carlo V di Francia e vescovo di Lisieux. Viene considerato uno dei principali fondatori e divulgatori delle scienze moderne e uno dei più originali pensatori del XIV secolo, è considerato un filosofo della Scolastica.

Nicola d’Oresme, matematico Nel Tractatus de configurationibus qualitatum et motuum, Questiones super geometriam Euclidis elaborò metodi per le somme infinite che prepararono la via per il calcolo infinitesimale di Cartesio e Galileo. Dimostrò la divergenza della serie armonica, utilizzando il metodo standard insegnato ancora oggi nelle lezioni di calcolo.

Infinitesimi in geometria: Cavalieri e i suoi indivisibili n Bonaventura Cavalieri (Milano 1589 ca. - Bologna 1647). La sua fama è legata soprattutto al “metodo degli indivisibili” rigorosamente sviluppato nell'opera Geometria indivisibilibus continuorum nova quadam ratione promota (1635) n Considerò qualsiasi grandezza geometrica – linee, piani, solidi – come l’insieme di costituenti elementari quali punti, linee e piani che vengono denominati “infiniti indivisibili”. Gesuita, di formazione umanistica, si dedicò alla predicazione, ma compì anche studi matematici a Pisa, dove fu allievo di Galileo Galilei. Nel 1629 ottenne a Bologna la cattedra di matematica che conservò fino alla morte. Cavalieri compì anche importanti ricerche nei campi della trigonometria piana e sferica, del calcolo logaritmico, dell'ottica e dell'astronomia.

Infinitesimi in geometria: Cavalieri e i suoi indivisibili n La teoria sollevò aspre polemiche tra i contemporanei, ma influì notevolmente sullo sviluppo della geometria e costituì un’anticipazione dei principi che avrebbero ispirato il calcolo infinitesimale.

Infiniti: 1694: Tacquet tra finito e infinito n Nel 1694 Andrea Tacquet notava: “Con facilità si passa da una progressione finita alla progressione infinita. E c’è da stupirsi che gli Aritmetici che conoscevano il teorema sulle progressioni finite abbiano ignorato quello sulle progressioni infinite, che si deduce immediatamente”.

Infinitesimi: Newton e Leibniz n La messa a punto dei principali concetti e dei procedimenti dell’analisi infinitesimale, almeno per quanto riguarda la loro interpretazione seicentesca, fu opera di Isaac Newton (16421727) e di Gottfried Wilhelm Leibniz (1646 -1716).

Newton e Leibniz Cronologicamente, Newton lavorò sul metodo diretto e inverso delle flussioni a partire dal 1665, ma ritardò la diffusione dei propri risultati; pubblicò Philosophiae Naturalis Principia Mathematica (1686 -1687) e Tractatus de quadratura curvarum (1704). L’opera Methodus fluxionum et serieruminfinitarum fu pubblicata soltanto postuma nel 1736. Con i lavori di Newton il calcolo poteva essere considerato concettualmente a punto. Ma sarà Leibniz che darà ordine di metodo ed introdurrà una simbologia efficace.

Dove porta il metodo: Newton fisico e matematico “Le differenze tra Leibniz e Newton spiegano la diversa influenza che i due pensatori hanno esercitato sullo sviluppo della scienza. Leibniz tende sistematicamente alla generalità, (…) Newton – mente inglese, portata alla considerazione del particolare concreto – lavora di solito sopra esempi tratti dal campo algebrico, (…) ma proprio questi esempi portano a questioni che esorbitano dalla generalità leibniziana" (Enriques, 1938, p. 63). L’impostazione newtoniana del Calcolo superava nettamente in flessibilità ed in profondità quella attribuita alla matematica greca che riguardava questioni statiche e non cinematiche

Newton e la gravitazione “Se la vaga concezione di una forza attrattiva governatrice dei movimenti celesti, la quale era per così dire nell’aria durante la seconda metà del secolo XVII, poté mutarsi nella solida teoria della gravitazione universale, fu perché Newton disponeva di un ordigno matematico delicato e rigoroso, cioè il calcolo delle flussioni; in tal modo alla geometria del cielo, in cui s’illustrarono gli astronomi greci, poté venire aggiunta la meccanica celeste, scienza ben meritevole dell’epiteto di sublime, in quanto permette non soltanto di spiegare, ma di preannunziare i fenomeni aventi per teatro il cielo” (Loria, 1938, p. 136).

Dove porta il metodo: Gli infinitesimi di Leibniz Per Leibniz la derivata è, per definizione, il rapporto tra l’infinitesimo dy e l’infinitesimo dx: Un esempio: la funzione y=x 2 raccogliendo ora a fattore dx nel numeratore si ottiene

La duplice natura degli infinitesimi A questo punto Leibniz considera dx infinitesimo e quindi trascurabile rispetto al numero reale 2 x, dunque la derivata vale: Tutto ciò lascia quanto meno perplessi…

La critica di Berkeley Quando si divide per dx si presuppone che sia diverso da zero, e quando si elimina il dx si presuppone che sia uguale a zero; gli infinitesimi sono dunque entità contradditorie. Berkeley definisce ironicamente gli infinitesimi ghosts of departed quantities (fantasmi di entità defunte).

Con gli infinitesimi di Leibniz… … salta l’archimedeità per i reali, in base alla quale per ogni numero reale a, esiste un numero naturale n tale che a sia maggiore del reciproco di n. Questa proprietà non può valere per gli infinitesimi dato che Leibniz aveva definito gli infinitesimi come i più piccoli numeri immaginabili e quindi non potevano esistere numeri reali minori.

Come superare l’impasse abolire gli infinitesimi e rifondare il calcolo su nuove basi (la strada scelta da Cauchy e Weierstrass nell’Ottocento); ridefinire in modo rigoroso i concetti di infinitesimo e di derivata (è la strada di Abraham Robinson negli anni Sessanta del XX secolo). Nel frattempo però…

Serie con somma infinita: Guido Grandi n Nel 1703 pubblicò il libro La quadratura del cerchio e dell’iperbole, al cui interno scoprì lo stesso paradosso matematico intuito anche da Leibniz, ossia che la somma di una serie a segni alterni di numeri può non convergere (serie di Grandi) Luigi Guido Grandi, al secolo Francesco Lodovico Grandi (Cremona, 1º ottobre 1671 – Pisa, 4 luglio 1742). Compì i suoi primi studi di grammatica sotto la guida del giovane letterato Giambattista Canneti e poi nel locale Collegio dei Gesuiti, dove ebbe come maestro il futuro matematico Giovanni Girolamo Saccheri. All’età di 16 anni entrò nel monastero camaldolese di Classe in Ravenna, assumendo il nome Guido in sostituzione degli originari Francesco Lodovico, e qui ritrovò l’antico maestro divenuto padre Pietro Canneti. Proseguiti gli studi teologici a Roma e quelli geometrici e matematici a Firenze, nel 1700 divenne professore di filosofia nel monastero camaldolese di Firenze.

Serie di Grandi La somma infinita 1 − 1 +. . . (simile alla serie 1 − 2 + 3 − 4 + · · ·) non si può sommare. Essa si può rappresentare con la formula: Con linguaggio moderno diremmo la successione delle sue somme parziali non possiede limite. In un senso esteso però si può dire che la sua somma di Cesàro (limite del valor medio delle somme parziali) è 1/2.

Contare senza sommare: Cantor e l’infinito attuale n Alla fine dell’Ottocento il matematico tedesco George Cantor, studiando il possibile numero di discontinuità nella convergenza delle serie di Fourier si imbatte ne “il numero dei naturali…+1” n Nell’introdurre l’insieme derivato, ossia l’insieme dei punti di accumulazione di un insieme dato, scopre e costruisce insiemi che “spariscono” dopo essere stati derivati tante volte quanti i numeri naturali… +1! n È la nascita degli ordinali transfiniti: ω+1, ω+2, ω+3

Cantor e i suoi ordinali n Per gli ordinali di Cantor non vale la proprietà commutativa: ω+1>1+ω. n Invece: 1+ ω = ω. n Cantor delinea l’algebra degli ordinali transfiniti.

Contare e sommare: Cantor: dagli ordinali ai cardinali n Se si prescinde dall’ordine allora gli insiemi hanno un loro CARDINALE, che definisce la numerosità dell’INSIEME. n EQUIPOTENZA: due insiemi sono equipotenti se possono essere messi in corrispondenza biunivoca tra di loro. n Naturali, interi, razionali hanno la stessa potenza, quindi lo stesso cardinale. n I reali non sono equipotenti ai naturali: devono avere un altro cardinale. n. Si lavora con gli INFINITI

Il recupero degli infinitesimi: Robinson e l’analisi non-standard n Intorno agli anni ’ 60 del XX secolo Abraham Robinson, un logico matematico tedesco emigrato negli USA, scoprì che tutti gli insiemi numerici potevano essere estesi con numeri “non standard” che ne ereditavano le proprietà. n Per l’insieme dei numeri reali questi altro non erano che gli infinitesimi di Leibniz, definiti questa volta in modo assolutamente rigoroso; diventava così possibile fondare nuovamente l'Analisi sul concetto di infinitesimo, cosa che Robinson fece nel suo libro Non standard Analysis (1966). n “Analisi non standard” è il nome dato a questa nuova formulazione dell’Analisi. Definizioni e dimostrazioni ritrovano la semplicità e la linearità che era del calcolo di Leibniz.

Robinson e l’infinitesimo attuale Secondo Robinson un infinitesimo è un numero ε minore in valore assoluto di qualsiasi 1/n per ogni n. A differenza di Leibniz, egli attribuisce a tali ε la dignità di numeri. La categoria dei NUMERI IPERREALI è l’insieme dei reali, degli infinitesimi, dei reciproci degli infinitesimi (numeri infiniti) e di altri numeri infinitamente vicini ai reali. Un numero iperreale non infinito è, pertanto, della forma: a+ε dove a è un numero reale ed ε un infinitesimo. Di conseguenza, attorno ad un numero reale, esiste un intorno di numeri iperreali a distanza infinitesima da esso, i quali costituiscono l'insieme degli a + ε: tale insieme viene detto monade e viene indicato con μ (a). Si dimostra che ε è minore di ogni numero reale positivo.

La derivata secondo Robinson A questo punto la nuova definizione di derivata è semplicemente Nell’esempio della funzione y = x 2 l’eliminazione finale dell’infinitesimo dx è ora pienamente giustificata.

La derivata secondo Robinson Per Robinson quindi gli infinitesimi sono definitivamente diversi da zero e la loro eliminazione è giustificata dall’uso della funzione st(_). Anche la definizione di integrale e la dimostrazione del teorema fondamentale del calcolo integrale risultano molto semplificate usando questa impostazione.

Si moltiplicano le rifondazioni dell’analisi Negli anni ’ 70 il matematico inglese John Conway inventa i numeri surreali, un’estensione degli iperreali. Sarebbero piaciuti a Dalì e a De Chirico, se avessero capito qualcosa di matematica

La Smooth Infinitesimal Analysis (SIA) Sempre negli anni ’ 70 si sviluppa la SIA, che porta alle estreme conseguenze il concetto di continuità con il principio di microlinearità. Conseguenza di questo principio è l’esistenza di numeri non nulli a quadrato nullo: L’insieme delle grandezze dx diverse da zero per le quali è dx 2=0 è non vuoto. Si rinuncia al principio del terzo escluso: due numeri o sono esattamente uguali, o differiscono per un infinitesimo e quindi sono indistinguibili o differiscono per un numero finito e quindi sono diversi.

L’algebra degli infinitesimi nella SIA Poiché dx 2=0 l’algebra degli infinitesimi risulta semplificata (x+dx)2 = x 2+2 xdx+dx 2 = x 2+2 xdx (x+dx)3 = x 3+3 x 2 dx+3 xdx 2+dx 3 = x 3+3 x 2 dx (x+dx)n = … = xn+nxn-1 dx

E i limiti nella SIA? Il numero di Nepero e diventa

La derivata nella SIA? La derivata viene definita in maniera implicita: f(x+dx)=f(x)+f’(x)dx Si evita la definizione esplicita che comporta la divisione per un infinitesimo, indistinguibile da zero.

Alcuni esempi Se f(x)=x 2 allora (x+dx)2=x 2+f’(x)dx porge x 2+2 xdx =x 2+f’(x)dx da cui 2 x=f’(x) Se f(x)=sin(x) allora sin(x+dx)=sin(x)+f’(x)dx porge sin(x)cos(dx)+cos(x)sin(dx)=sin(x)+f’(x)dx da cui sin(x)+cos(x)dx=sin(x)+f’(x)dx da cui cosx=f’(x) Se f(x)=ex allora e(x+dx)=ex+f’(x)dx porge exedx=ex+f’(x)dx da cui ex(1+dx)=ex+f’(x)dx da cui ex=f’(x)

Dov’è il trucco? Come può essere tutto così semplice? È il ritorno a Leibniz la chiave di tutto? Robinson mantiene gli infinitesimi e giustifica l’eliminazione del dx con la regola della parte standard. Nella SIA l’eliminazione del dx è preventiva, si fa dall’inizio ponendo dx 2=0. Sono solo trucchi?

Conclusione Sarebbe ipotizzabile un percorso didattico che approdi allo studio di funzioni reali di variabile reale passando per gli infinitesimi di Robinson o per la SIA? Quali sarebbero le conseguenze a livello didattico?