La circonferenza nel piano cartesiano La circonferenza il

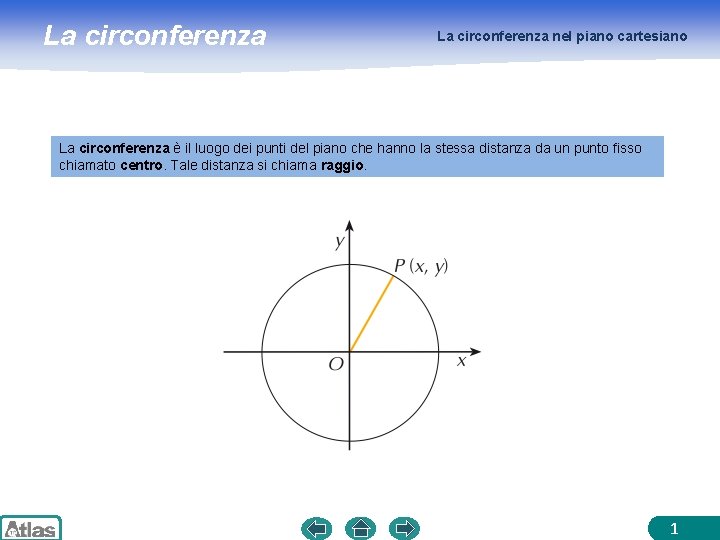
La circonferenza nel piano cartesiano La circonferenza è il luogo dei punti del piano che hanno la stessa distanza da un punto fisso chiamato centro. Tale distanza si chiama raggio. 1

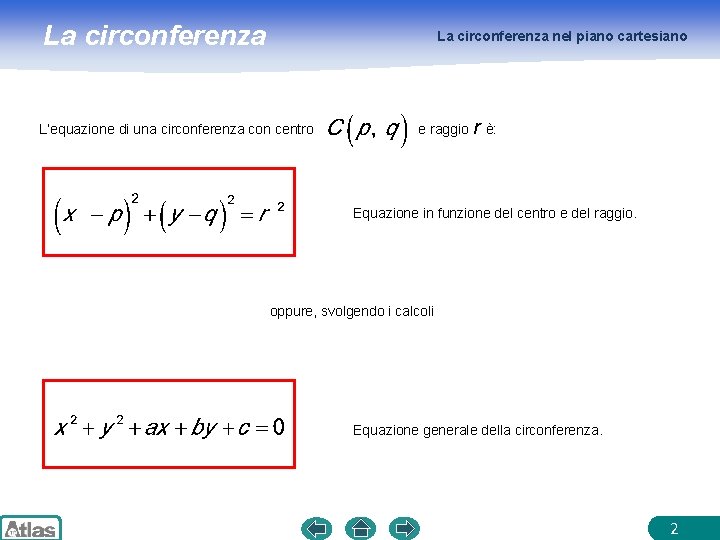
La circonferenza nel piano cartesiano L’equazione di una circonferenza con centro e raggio r è: Equazione in funzione del centro e del raggio. oppure, svolgendo i calcoli Equazione generale della circonferenza. 2

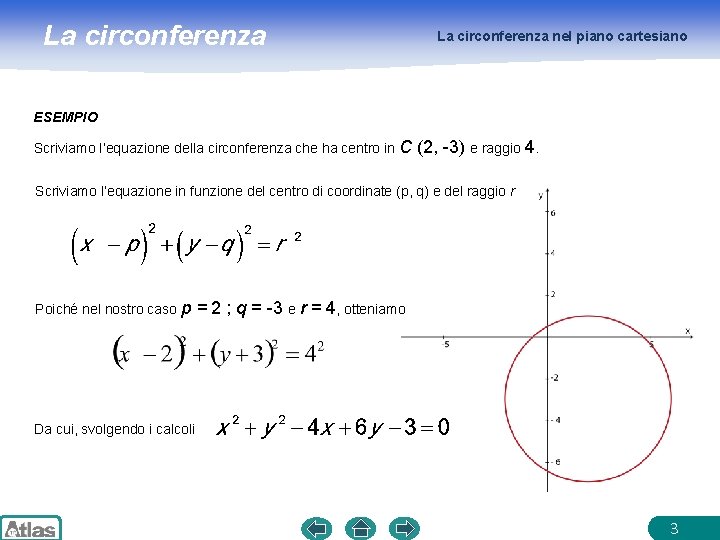
La circonferenza nel piano cartesiano ESEMPIO Scriviamo l’equazione della circonferenza che ha centro in C (2, -3) e raggio 4. Scriviamo l’equazione in funzione del centro di coordinate (p, q) e del raggio r Poiché nel nostro caso p = 2 ; q = -3 e r = 4, otteniamo Da cui, svolgendo i calcoli 3

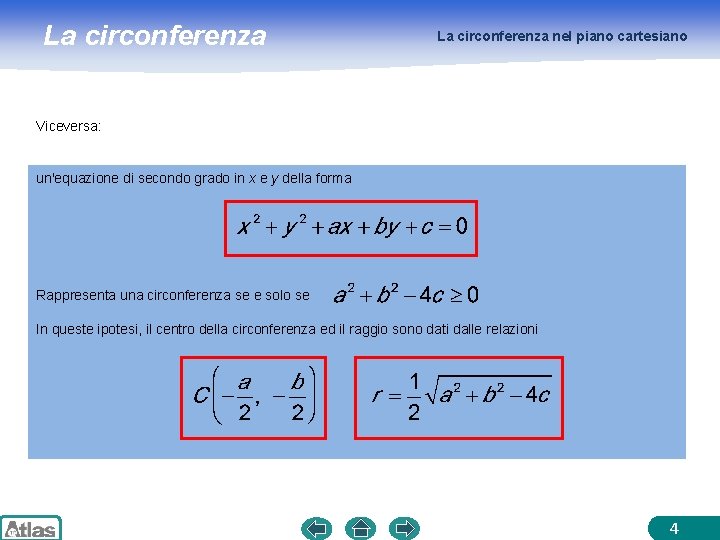
La circonferenza nel piano cartesiano Viceversa: un'equazione di secondo grado in x e y della forma Rappresenta una circonferenza se e solo se In queste ipotesi, il centro della circonferenza ed il raggio sono dati dalle relazioni 4

La circonferenza nel piano cartesiano ESEMPI • L’equazione non rappresenta una circonferenza perché è una circonferenza di centro e raggio 5

La circonferenza nel piano cartesiano ESEMPIO L’equazione rappresenta una circonferenza? Scriviamola nella forma ottenuta dividendo entrambi i membri per 4. Tale equazione rappresenta una circonferenza, perché Essa ha centro in e raggio r=2 6

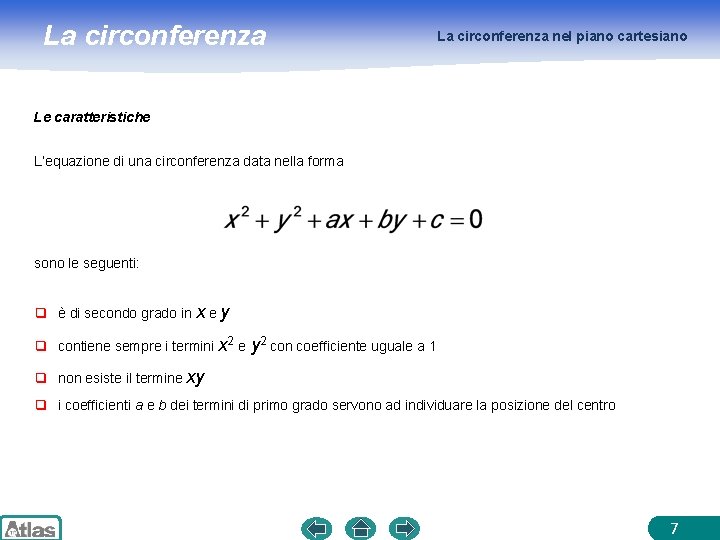
La circonferenza nel piano cartesiano Le caratteristiche L’equazione di una circonferenza data nella forma sono le seguenti: q è di secondo grado in x e y q contiene sempre i termini x 2 e y 2 con coefficiente uguale a 1 q non esiste il termine xy q i coefficienti a e b dei termini di primo grado servono ad individuare la posizione del centro 7

La circonferenza nel piano cartesiano I casi particolari Al variare dei valori assunti dai parametri a, b, c dell’equazione abbiamo situazioni diverse: q se a = 0, l’ascissa del centro vale 0 e quindi il centro della circonferenza appartiene all’asse delle ordinate q se b = 0, l’ordinata del centro vale 0 e quindi il centro della circonferenza appartiene all’asse delle ascisse q se c = 0, la circonferenza passa per l’origine 8

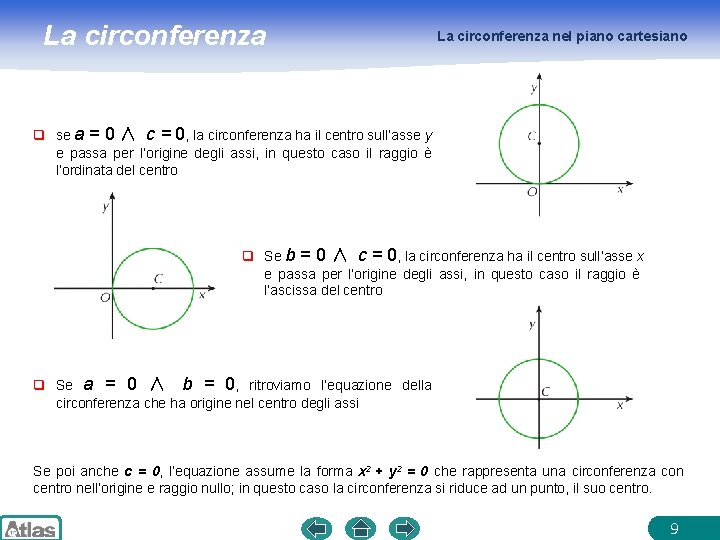
La circonferenza nel piano cartesiano q se a = 0 ∧ c = 0, la circonferenza ha il centro sull’asse y e passa per l’origine degli assi, in questo caso il raggio è l’ordinata del centro q Se b = 0 ∧ c = 0, la circonferenza ha il centro sull’asse x e passa per l’origine degli assi, in questo caso il raggio è l’ascissa del centro q Se a = 0 ∧ b = 0, ritroviamo l’equazione della circonferenza che ha origine nel centro degli assi Se poi anche c = 0, l’equazione assume la forma x 2 + y 2 = 0 che rappresenta una circonferenza con centro nell’origine e raggio nullo; in questo caso la circonferenza si riduce ad un punto, il suo centro. 9

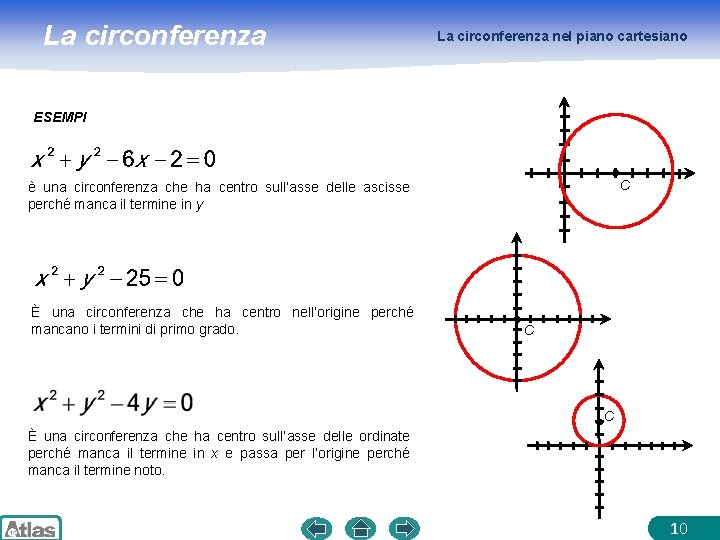
La circonferenza nel piano cartesiano ESEMPI C è una circonferenza che ha centro sull’asse delle ascisse perché manca il termine in y È una circonferenza che ha centro nell’origine perché mancano i termini di primo grado. C C È una circonferenza che ha centro sull’asse delle ordinate perché manca il termine in x e passa per l’origine perché manca il termine noto. 10

La circonferenza Come determinare l’equazione di una circonferenza Per trovare l’equazione di una circonferenza sono necessarie e sufficienti tre informazioni indipendenti; in particolare: • Se si conoscono le coordinate (p, q) del centro e la misura r del raggio, la sua equazione è • Se si conoscono le coordinate di tre punti, basta sostituire tali coordinate nell’equazione generale della circonferenza e risolvere il sistema ottenuto. 11

La circonferenza Come determinare l’equazione di una circonferenza ESEMPIO Determiniamo l’equazione della circonferenza di centro C (1, 2) passante per A (0, 4) Possiamo risolvere il problema in due modi: 1° METODO (Geometrico) Calcoliamo il raggio della circonferenza corrispondente al segmento CA: A C L’equazione della circonferenza è allora: 12

La circonferenza Come determinare l’equazione di una circonferenza 2° METODO (Algebrico) Scriviamo il sistema: L’ascissa del centro vale 1 L’ordinata del centro vale 2 La circonferenza passa per A Il sistema risolto dà: L’equazione è dunque 13

La circonferenza Come determinare l’equazione di una circonferenza ESEMPIO Scriviamo l’equazione della circonferenza che passa per i punti: A (-4, 0), B (-1, -1), C (0, 2) Per tre punti non allineati passa una sola circonferenza. Possiamo verificare il non allineamento dei punti mediante la rappresentazione dei punti nel piano cartesiano. C A B 14

La circonferenza Come determinare l’equazione di una circonferenza Scriviamo il sistema sfruttando la condizione di appartenenza di un punto a una circonferenza: Passaggio per A Passaggio per B Passaggio per C C Risolvendo il sistema abbiamo: A B La circonferenza ha dunque equazione 15

La circonferenza Posizioni reciproche di una circonferenza e una retta Una retta rispetto ad una circonferenza si dice: q secante se le due curve hanno due punti di intersezione distinti; q tangente se le due curve hanno un solo punto in comune; q esterna se le due curve non si intersecano. 16

La circonferenza Posizioni reciproche di una circonferenza e una retta Per determinare le coordinate dei punti di intersezione, se esistono, tra una retta e una circonferenza, possiamo agire in due modi. 1° METODO Scriviamo il sistema delle equazioni delle due curve: Applicando il metodo di sostituzione e sostituendo nella prima equazione al posto di y (o di x) l’espressione ricavata dalla seconda si ottiene l’equazione risolvente del sistema che è di secondo grado. 17

La circonferenza Posizioni reciproche di una circonferenza e una retta Se nell’equazione risolvente: q Δ > 0, il sistema ha due soluzioni reali distinte, le due curve hanno due punti distinti di intersezione quindi la retta è secante rispetto alla circonferenza; q Δ = 0, il sistema ha due soluzioni reali coincidenti, le due curve hanno allora un solo punto di intersezione, quindi la retta è tangente alla circonferenza; q Δ < 0, il sistema non ha soluzioni reali, le due curve non hanno punti di intersezione, quindi la retta è esterna alla circonferenza. 18

La circonferenza Posizioni reciproche di una circonferenza e una retta 2° METODO Utilizziamo considerazioni di tipo geometrico: q se la retta è secante la circonferenza, allora la distanza dal centro della retta è minore del raggio; q se la retta è tangente alla circonferenza, allora la distanza è uguale al raggio; q se la retta è esterna alla circonferenza, allora la distanza è maggiore del raggio. 19

La circonferenza Posizioni reciproche di una circonferenza e una retta Poiché sappiamo calcolare la distanza di un punto da una retta con la formula: Possiamo calcolare la distanza del centro della circonferenza dalla retta e confrontarla con il raggio per dedurne la posizione. 20

La circonferenza Posizioni reciproche di una circonferenza e una retta ESEMPIO Data la circonferenza di centro C di equazione x (1, -2) e raggio r = 3 vogliamo sapere qual è la posizione della retta – y + 2 = 0 rispetto ad essa. Non è necessario trovare l’equazione della circonferenza; basta infatti calcolare la distanza di retta C dalla e confrontarla con il raggio (metodo geometrico). Poiché possiamo concludere che la retta è esterna alla circonferenza. 21

La circonferenza Posizioni reciproche di una circonferenza e una retta ESEMPIO Troviamo le coordinate degli eventuali punti di intersezione tra la circonferenza di equazione e la retta di equazione Poiché dobbiamo individuare le coordinate dei punti di intersezione conviene risolvere il problema con il metodo algebrico. Scriviamo il sistema formato dalle equazioni date: 22

La circonferenza Posizioni reciproche di una circonferenza e una retta Applichiamo il metodo di sostituzione e otteniamo Svolgendo i calcoli nell’equazione risolvente otteniamo Questa equazione ammette due soluzioni reali distinte. Le corrispondenti soluzioni del sistema sono: I punti di intersezione sono quindi 23

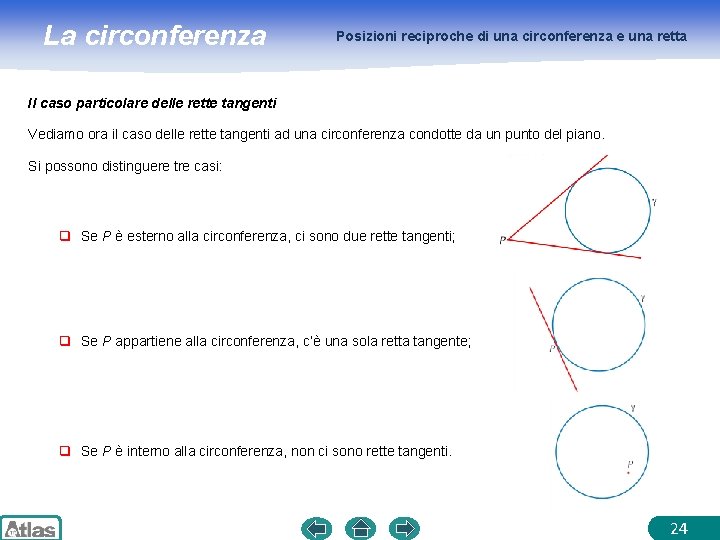
La circonferenza Posizioni reciproche di una circonferenza e una retta Il caso particolare delle rette tangenti Vediamo ora il caso delle rette tangenti ad una circonferenza condotte da un punto del piano. Si possono distinguere tre casi: q Se P è esterno alla circonferenza, ci sono due rette tangenti; q Se P appartiene alla circonferenza, c’è una sola retta tangente; q Se P è interno alla circonferenza, non ci sono rette tangenti. 24

La circonferenza Posizioni reciproche di una circonferenza e una retta Per trovare la retta tangente ad una circonferenza passante per un punto P del piano possiamo procedere in due modi: Metodo geometrico Metodo algebrico • • Scrivere il sistema tra l’equazione della circonferenza e quella del fascio di rette di centro P e si trova l’equazione risolvente. • Si calcola la distanza del centro della circonferenza dalla generica retta del fascio di centro P • Si impone che tale distanza sia uguale al raggio Si impone Δ = 0 25

La circonferenza Posizioni reciproche di una circonferenza e una retta ESEMPIO Data la circonferenza di equazione tangenti, passanti per il punto P vogliamo scrivere le equazioni delle rette ad essa (4, 0) Il punto P è esterno alla circonferenza. P 1° METODO (Algebrico) Scriviamo l’equazione del fascio di rette di centro P Equazione risolvente: Le equazioni delle rette tangenti sono: 26

La circonferenza Posizioni reciproche di una circonferenza e una retta 2° METODO (Geometrico) Scriviamo l’equazione del fascio in forma implicita Centro della circonferenza C (0, 0) raggio r=2 Distanza del centro dal fascio Equazione da risolvere 27

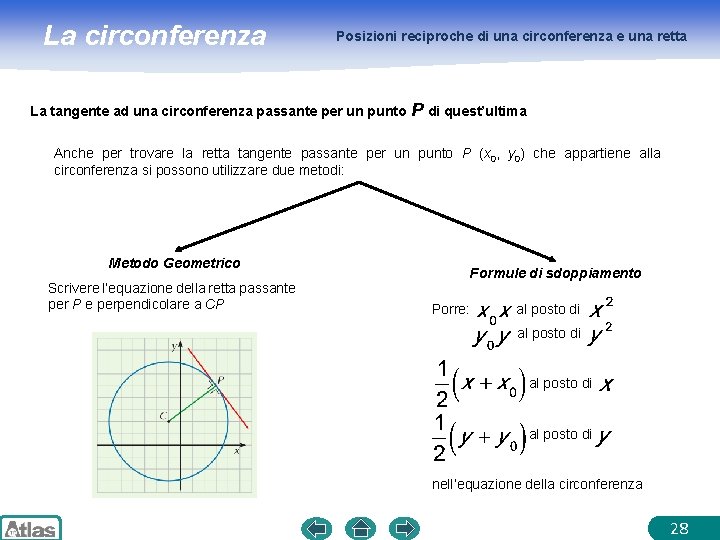
La circonferenza Posizioni reciproche di una circonferenza e una retta La tangente ad una circonferenza passante per un punto P di quest’ultima Anche per trovare la retta tangente passante per un punto P (x 0, y 0) che appartiene alla circonferenza si possono utilizzare due metodi: Metodo Geometrico Scrivere l’equazione della retta passante per P e perpendicolare a CP Formule di sdoppiamento Porre: al posto di nell’equazione della circonferenza 28

La circonferenza Posizioni reciproche di una circonferenza e una retta ESEMPIO Troviamo l’equazione della retta tangente alla circonferenza di equazione nel suo punto P (2; 2) Con le formule di sdoppiamento Poniamo: al posto di Otteniamo così l’equazione: 29

La circonferenza Posizioni reciproche di una circonferenza e una retta Con il metodo Geometrico Coordinate del centro della circonferenza: C (4, 0) Retta tangente: retta per P di coefficiente angolare 1 30