I numeri complessi La forma algebrica Lunit immaginaria

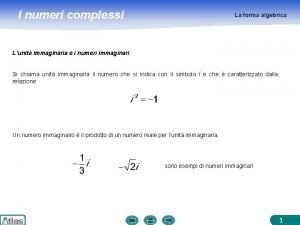
I numeri complessi La forma algebrica L’unità immaginaria e i numeri immaginari Si chiama unità immaginaria il numero che si indica con il simbolo i e che è caratterizzato dalla relazione Un numero immaginario è il prodotto di un numero reale per l’unità immaginaria. sono esempi di numeri immaginari 1

I numeri complessi La forma algebrica Le proprietà dell’unità immaginaria Infatti Le potenze dell’unità immaginaria sono cicliche di periodo 4, infatti: 2

I numeri complessi Le operazioni con i numeri immaginari Nel calcolo, il numero i si tratta come una qualsiasi altra lettera e si applicano ad esso le regole del calcolo algebrico. 3

I numeri complessi Le operazioni con i numeri immaginari ESEMPI Proprietà invariantiva della divisione 4

I numeri complessi Si chiama numero complesso la somma di un numero reale con un numero immaginario; un numero complesso assume quindi la forma con a è la parte reale bi è la parte immaginaria L’insieme dei numeri complessi si indica con la lettera C sono esempi di numeri complessi se otteniamo un numero immaginario se otteniamo un numero reale 5

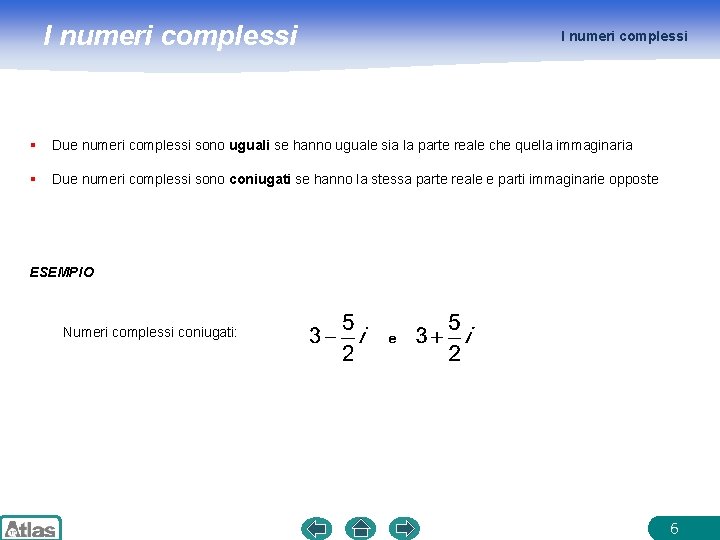
I numeri complessi § Due numeri complessi sono uguali se hanno uguale sia la parte reale che quella immaginaria § Due numeri complessi sono coniugati se hanno la stessa parte reale e parti immaginarie opposte ESEMPIO Numeri complessi coniugati: 6

I numeri complessi Le operazioni con i numeri complessi Introduciamo ora le operazioni tra numeri complessi che godono delle stesse proprietà formali di cui godono quelle definite in R. § Addizione e sottrazione: ESEMPIO 7

I numeri complessi § Le operazioni con i numeri complessi Moltiplicazione: ESEMPIO 8

I numeri complessi § Le operazioni con i numeri complessi Divisione: si esegue moltiplicando dividendo e divisore per il complesso coniugato del divisore: ESEMPIO 9

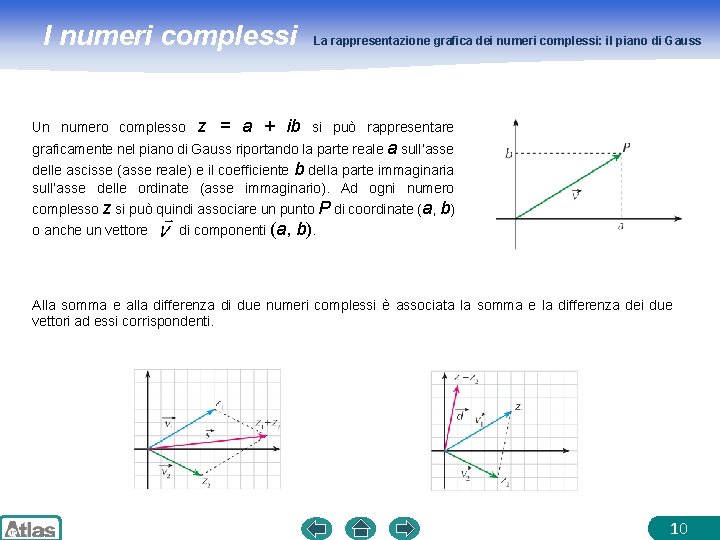
I numeri complessi Un numero complesso z = a + ib La rappresentazione grafica dei numeri complessi: il piano di Gauss si può rappresentare graficamente nel piano di Gauss riportando la parte reale a sull’asse delle ascisse (asse reale) e il coefficiente b della parte immaginaria sull’asse delle ordinate (asse immaginario). Ad ogni numero complesso z si può quindi associare un punto P di coordinate (a, b) o anche un vettore di componenti (a, b). Alla somma e alla differenza di due numeri complessi è associata la somma e la differenza dei due vettori ad essi corrispondenti. 10

I numeri complessi Ad ogni numero complesso La forma trigonometrica z = a + ib si può associare la forma trigonometrica: Dove ρ rappresenta il modulo e ϑ è l’argomento o anomalia. Per passare dalla forma algebrica a quella trigonometrica possiamo utilizzare le relazioni: (per il teorema di Pitagora) (per i teoremi di trigonometria sui triangoli rettangoli) 11

I numeri complessi La rappresentazione grafica dei numeri complessi: il piano di Gauss ESEMPIO Dato il numero complesso si ha che: La sua forma trigonometrica è quindi 12

I numeri complessi La rappresentazione grafica dei numeri complessi: il piano di Gauss Viceversa se il numero complesso è dato in forma trigonometrica, basta calcolare i valori di sinϑ e cosϑ ed eseguire le operazioni indicate per ottenere la forma algebrica. ESEMPIO Il numero complesso z la cui forma trigonometrica è ha forma algebrica 13

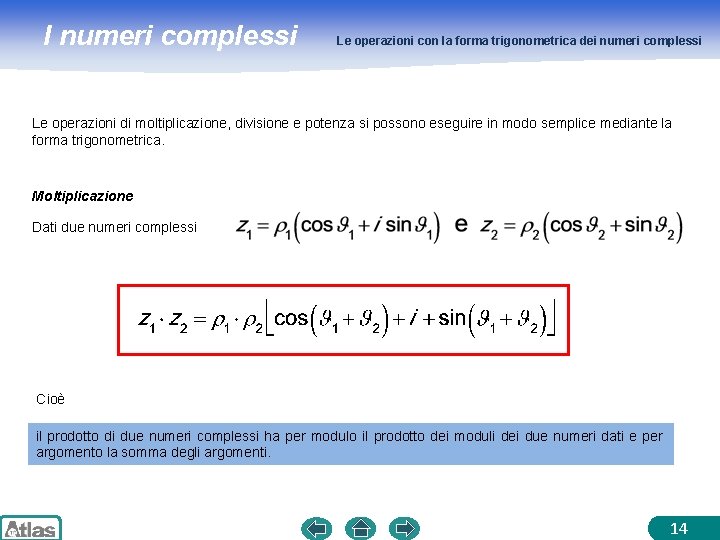
I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi Le operazioni di moltiplicazione, divisione e potenza si possono eseguire in modo semplice mediante la forma trigonometrica. Moltiplicazione Dati due numeri complessi Cioè il prodotto di due numeri complessi ha per modulo il prodotto dei moduli dei due numeri dati e per argomento la somma degli argomenti. 14

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi ESEMPIO 15

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi Divisione Cioè il quoziente di due numeri complessi è il numero complesso che ha per modulo il quoziente dei moduli e per argomento la differenza degli argomenti dei due numeri dati. In particolare, il reciproco di un numero complesso di modulo ρ e argomento ϑ ha modulo e argomento – ϑ cioè: 16

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi ESEMPIO 17

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi Potenza La potenza ennesima, con n intero positivo, di un numero complesso è data dalla formula di De Moivre: Si pone per definizione Inoltre 18

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi ESEMPIO • Calcoliamo ora 19

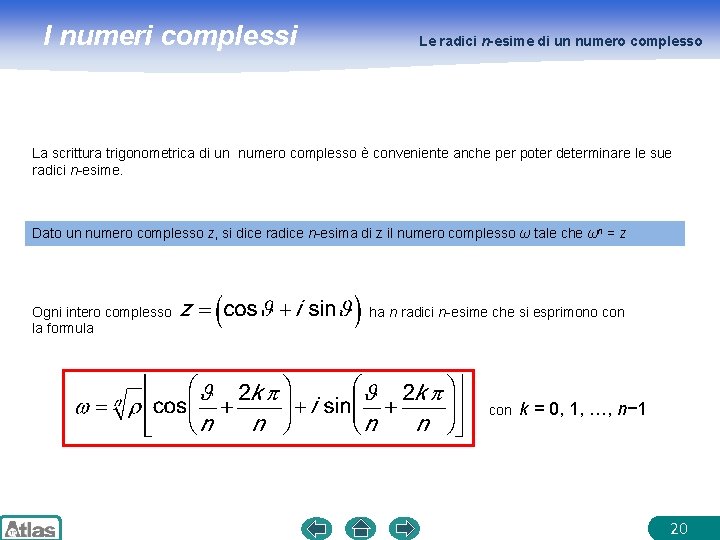
I numeri complessi Le radici n-esime di un numero complesso La scrittura trigonometrica di un numero complesso è conveniente anche per poter determinare le sue radici n-esime. Dato un numero complesso z, si dice radice n-esima di z il numero complesso ω tale che ωn = z Ogni intero complesso la formula ha n radici n-esime che si esprimono con k = 0, 1, …, n− 1 20

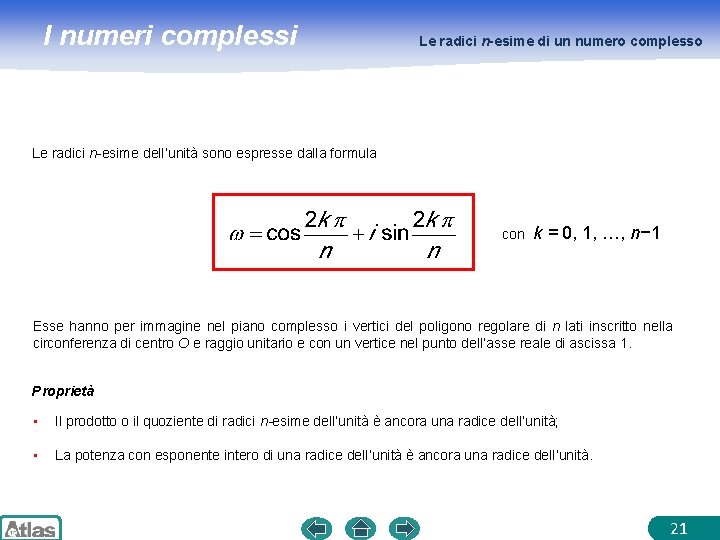
I numeri complessi Le radici n-esime di un numero complesso Le radici n-esime dell’unità sono espresse dalla formula con k = 0, 1, …, n− 1 Esse hanno per immagine nel piano complesso i vertici del poligono regolare di n lati inscritto nella circonferenza di centro O e raggio unitario e con un vertice nel punto dell’asse reale di ascissa 1. Proprietà • Il prodotto o il quoziente di radici n-esime dell’unità è ancora una radice dell’unità; • La potenza con esponente intero di una radice dell’unità è ancora una radice dell’unità. 21

I numeri complessi Le radici n-esime di un numero complesso Le radici n-esime dell’unità sono strettamente legate alle radici dello stesso indice di qualunque numero complesso. le radici n-esime di un numero complesso z si ottengono tutte da una qualunque di esse moltiplicandola per le radici n-esime dell'unità. Si ha cioè che, indicate con ω0, ω1, …. . ωn-1 le radici dell’unità e con μ una qualunque radice di z, le radici n-esime di z sono date da ESEMPIO Calcoliamo le radice seste di 64. Essendo 26 = 64, una radice particolare è 2. Le radici seste dell’unità sono rappresentate dall’espressione Abbiamo quindi che: con k = 0, 1, …, n− 1 22

I numeri complessi Soluzioni di un’equazione Attraverso il calcolo delle radici n-esime di un numero complesso si possono trovare le n soluzioni di un’equazione algebrica di grado n. ESEMPIO Troviamo le soluzioni dell’equazione Poiché avremo Cioè 23

I numeri complessi La forma esponenziale di un numero completo è usata spesso nelle scienze applicate perché permette una ulteriore semplificazione del calcolo. Dato un numero complesso z di modulo ρ ed argomento ϑ si ha che Per eseguire prodotti, quozienti e potenze di numeri complessi in forma esponenziale, si applicano le proprietà delle potenze. Dati • prodotto • potenza n-esima Dalla forma esponenziale di un numero complesso, si ricavano le seguenti formule di Eulero: • quoziente 24

I numeri complessi Le operazioni con la forma trigonometrica dei numeri complessi ESEMPI • Scriviamo in forma algebrica il numero complesso • Scriviamo in forma esponenziale il numero complesso Si ha quindi 25