th 11 Phase Space Lec Collisionless Systems We




































































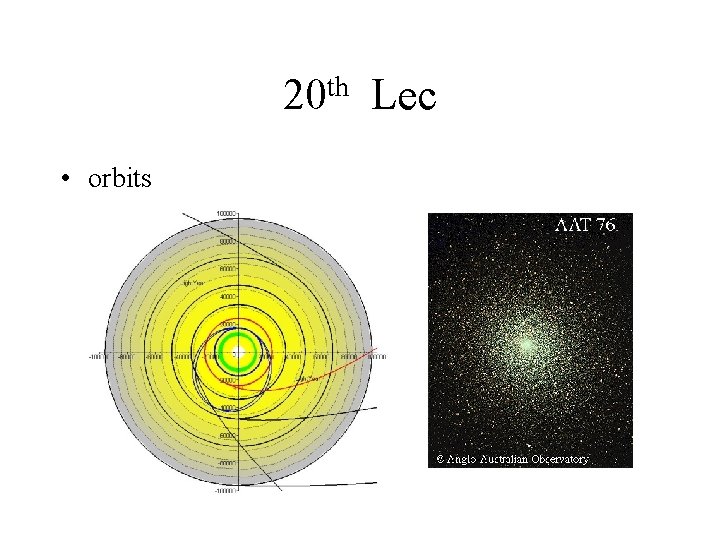





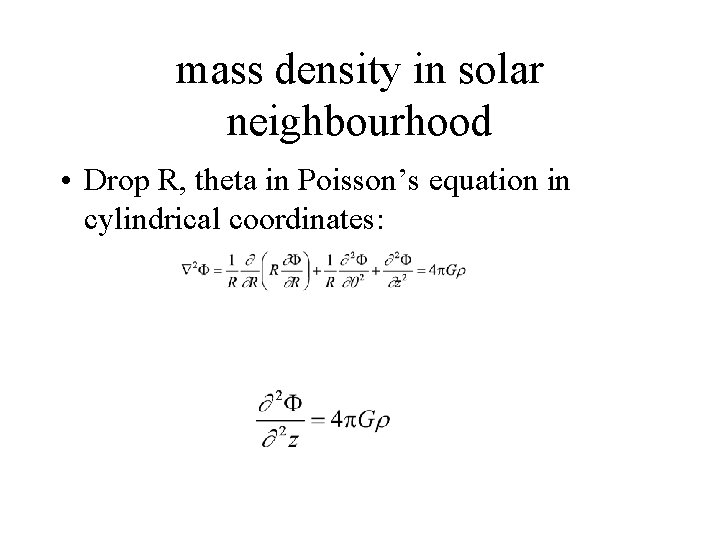







- Slides: 85

th 11 • Phase Space Lec

Collisionless Systems • We showed collisions or deflections are rare • Collisionless: stellar motions under influence of mean gravitational potential! • Rational: • Gravity is a long-distance force, decreases as r-2 – as opposed to the statistical mechanics of molecules in a box

Collisionless Systems • stars move under influence of a smooth gravitational potential – determined by overall structure of system • Statistical treatment of motions – collisionless Boltzman equation – Jeans equations

• provide link between theoretical models (potentials) and observable quantities. • instead of following individual orbits • study motions as a function of position in system • Use CBE, Jeans eqs. to determine mass distributions and total masses

Fluid approach: Phase Space Density PHASE SPACE DENSITY: Number of stars per unit volume per unit velocity volume f(x, v) (all called Distribution Function DF). The total number of particles per unit volume is given by:

• E. g. , air particles with Gaussian velocity (rms velocity = σ in x, y, z directions): • The distribution function f(x, v) is defined by: md. N=f(x, v)d 3 xd 3 v where d. N is the number of particles per unit volume with a given range of velocities.

• The total mass is then given by the integral of the mass distribution function over space and velocity volume: • Note: in spherical symmetry d 3 x=4πr 2 dr, • for isotropic systems d 3 v=4πv 2 dv • The total momentum is given by:

• Example: mean speed of air molecules in a box of dx 3 : These are gamma functions

• Gamma Functions:

How to calculate 3 dx and 3 dv

DF and its moments

Additive: subcomponents add up to the total gravitational mass

Full Notes online • http: //www-star. st-and. ac. uk/~hz 4/gravdyn/ Gravi. Dyn. Final 3. ppt Gravi. Dyn. Final 3. pdf

Liouvilles Theorem We previously introduced the concept of phase space density. The concept of phase space density is useful because it has the nice property that it is incompessible for collisionless systems. A COLLISIONLESS SYSTEM is one where there are no collisions. All the constituent particles move under the influence of the mean potential generated by all the other particles. INCOMPRESSIBLE means that the phase-space density doesn’t change with time.

Consider Nstar identical particles moving in a small bundle through spacetime on neighbouring paths. If you measure the bundles volume in phase space (Vol=Δx Δ p) as a function of a parameter λ (e. g. , time t) along the central path of the bundle. It can be shown that: px px x x It can be seen that the region of phase space occupied by the particle deforms but maintains its area. The same is true for y-py and z-pz. This is equivalent to saying that the phase space density f=Nstars/Vol is constant. df/dt=0!

motions in phase-space • Flow of points in phase space corresponding to stars moving along their orbits. • phase space coords: • and the velocity of the flow is then: – where wdot is the 6 -D vector related to w as the 3 -D velocity vector v relates to x

• stars are conserved in this flow, with no encounters, stars do not jump from one point to another in phase space. • they drift slowly through phase space • In the COMBINED potential of stars and dark matter

fluid analogy • regard stars as making up a fluid in phase space with a phase space density • • assume that f is a smooth function, continuous and differentiable – good for N >105

• as in a fluid, we have a continuity equation • fluid in box of volume V, density , and velocity v, the change in mass is then: – Used the divergence theorem

continuity equation • must hold for any volume V, hence: • in same manner, density of stars in phase space obeys a continuity equation: If we integrate over a volume of phase space V, then 1 st term is the rate of change of the stars in V, while 2 nd term is the rate of outflow/inflow of stars from/into V. 0

Collisionless Boltzmann Equation • Hence, we can simplify the continuity equation to the CBE: • Vector form

• in the event of stellar encounters, no longer collisionless • require additional terms to rhs of equation

CBE cont. • can define a Lagrangian derivative • Lagrangian flows are where the coordinates travel along with the motions (flow) – hence x= x 0 = constant for a given star • then we have: • and

incompressible flow • example of incompressible flow • idealised marathon race: each runner runs at constant speed • At start: the number density of runners is large, but they travel at wide variety of speeds • At finish: the number density is low, but at any given time the runners going past have nearly the same speed

DF & Integrals of motion • If some quantity I(x, v) is conserved i. e. • Assume f(x, v) depends on (x, v) through the function I(x, v), so f=f(I(x, v)). • Such phase space density is incompressible, i. e

Jeans theorem • For most stellar systems the DF depends on (x, v) through generally three integrals of motion (conserved quantities), Ii(x, v), i=1. . 3 f(x, v) = f(I 1(x, v), I 2(x, v), I 3(x, v)) • E. g. , in Spherical Equilibrium, f is a function of energy E(x, v) and ang. mom. vector L(x, v). ’s amplitude and z-component

3 D Analogy of 6 D Phase space • If DF(x, v) is analogous to density(x, y, z), • Then DF(E, L, Lz) is ~ density(r, theta, phi), • Integrals analogous to spherical coordinates – E(x, v) analogous to r(x, y, z) • Isotropic DF(E) ~ spherical density(r) – Normalization d. M=f(E)dx 3 dv 3 ~ d. M=density(r)dr 3 – Have non-self-gravitating subcomponents: DF 1+DF 2, like rho 1+rho 2 to make up total gravity.

th 12 • Phase Space Lec

Tensor Virial Theorem • Equation of motion: This is Tensor Virial Theorem

• E. g. • So the time averaged value of v 2 is equal to the time averaged value of the circular velocity squared.

Scalar Virial Theorem • the kinetic energy of a system with mass M is just where <v 2> is the mean-squared speed of the system’s stars. • Hence the virial theorem states that Virial

Stress Tensor • describes a pressure which is anisotropic – not the same in all directions • and we can refer to a “pressure supported” system • the tensor is symmetric. • can chose a set of orthogonal axes such that the tensor is diagonal • Velocity ellipsoid with semi-major axes given by

Subcomponents in Spherical Equilibrium Potential • Described by spherical potential φ(r) • SPHERICAL subcomponent density ρ(r) depends on modulus of r. • EQUILIBRIUM: Properties do not evolve with time.

• In a spherical potential So <xy>=0 since the average value of xy will be zero. <vxvy>=0

Spherical Isotropic f(E) Equilibrium Systems • ISOTROPIC: The distribution function f(E) only depends on the modulus of the velocity rather than the direction. Note: the tangential direction has and components

Anisotropic DF f(E, L) in spherical potential. • Energy E is conserved as: • Angular Momentum Vector L is conserved as: • DF depends on Velocity Direction through L=r X v • Hence anisotropic

e. g. , f(E, L) is an incompressible fluid • The total energy of an orbit is given by: 0 for static potential, 0 for spherical potential So f(E, L) constant along orbit or flow

• spherical Jeans eq. of a tracer density rho(r) • • Proof :

Jeans eq. Proof cont.

• SELF GRAVITATING: The masses are kept together by their mutual gravity. • In non-self gravitating systems the density that creates the potential is not equal to the density of stars. e. g a black hole with stars orbiting about it is NOT self gravitating.

th 13 • Phase Space Lec

Velocity dispersions of a subcomponent in spherical potential • For a spherically symmetric system we have • a non-rotating galaxy has – and the velocity ellipsoids are spheroids with their symmetry axes pointing towards the galactic centre • Define anisotropy

Spherical mass profile from velocity dispersions. • Get M(r) or Vcir from: • RHS: observations of dispersion and b as a function of radius r for a stellar population.

• Isotropic Spherical system, β=0 Note: 2=P • This is the isotropic JEANS EQUATION, relating the pressure gradient to the gravitational force. Above Solution to Isotropic Jeans Eq: negative sign has gone since we reversed the limits.

Hydrostatic equilibrium Isotropic spherical Jeans equation • Conservation of momentum gives:

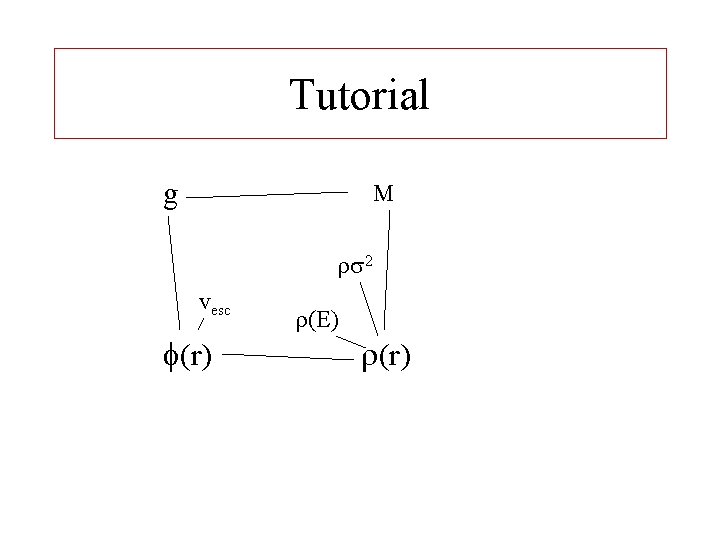
Tutorial g M 2 vesc (r) (E) (r)

Tutorial Question 3 • Question: Show dispersion sigma is constant in potential Phi=V 02 ln(r). What might be the reason that this model is called Singular Isothermal Sphere?


• • Since the circular velocity is independent of radius then so is the velocity dispersion Isothermal.

Flattened Disks • Here the potential is of the form (R, z). • No longer spherically symmetric. • Now it is Axisymmetric

Question 4: Oblate Log. potential • oblate galaxy with Vcirc ~ V 0 =100 km/s • Draw contours of the corresponding Selfgravitating Density to show it is unphysical. • Let Lz=1 kpc*V 0 , E=0. 55*V 02 +C 0, Plot effective potential contours in RZ plane to show it is an epicycle orbit. • Taylor expand the potential near (R, z)=(1, 0) to find epicycle frequencies and the approximate z-height and peri-apo range.

Orbits in Axisymmetric Potentials (disk galaxies) z y x q R 2=x 2+y 2 R • cylindrical (R, , z) symmetry z-axis • stars in equatorial plane: same motions as in spherically symmetric potential – non-closed rosette orbits • stars moving out of plane – can be reduced to 2 -D problem in (R, z) – conservation of z-angular momentum, L

• Angular momentum about the z-axis is conserved, toque(r F=0) if no dependence on . • Energy is also conserved (no time-dependence) Specific energy density in 3 D • Eliminating in the energy equation using conservation of angular momentum gives: eff

Total Angular momentum almost conserved • These orbits can be thought of as being planar with more or less fixed eccentricity. • The approximate orbital planes have a fixed inclination to the z axis but they process about this axis. • star picks up angular momentum as it goes towards the plane and returns it as it leaves.

Orbital energy • Energy of orbit is (per unit mass) • effective potential is the gravitational potential energy plus the specific kinetic energy associated with motion in direction • orbit bound within

• The angular momentum barrier for an orbit of energy E is given by • The effective potential cannot be greater than the energy of the orbit. • The equations of motion in the 2 D meridional (RZ)plane then become: .

• Thus, the 3 D motion of a star in an axisymmetric potential (R, z) can be reduced to the motion of a star in a plane (Rz). • This (non uniformly) rotating plane with cartesian coordinates (R, z) is often called the MERIDIONAL PLANE. • eff(R, z) is called the EFFECTIVE POTENTIAL. • The orbits are bound between two radii (where the effective potential equals the total energy) and oscillates in the z direction.

• The minimum in eff occurs at the radius at which a circular orbit has angular momentum Lz. • The value of eff at the minimum is the energy of this circular orbit. eff R E Rcir

• The effective potential is the sum of the gravitational potential energy of the orbiting star and the kinetic energy associated with its motion in the direction (rotation). • Any difference between eff and E is simply kinetic energy of the motion in the (R, z) plane. • Since the kinetic energy is non negative, the orbit is restricted to the area of the meridional plane satisfying E - eff. (R, z)>= 0 • The curve bounding this area is called the ZERO VELOCITY CURVE since the orbit can only reach this curve if its velocity is instantaneously zero.

Nearly circular orbits: epicycles • In disk galaxies, many stars (disk stars) are on nearly-circular orbits • Eo. M: • x=R-Rg – expand in Taylor series about (x, z)=(0, 0) – then

• When the star is close to z=0 the effective potential can be expanded to give Zero, changes sign above/below z=0 equatorial plane. So, the orbit is oscillating in the z direction. 2

epicyclic approximation • ignore all higher / cross terms: • Eo. M: harmonic oscillators – epiclyclic frequency : – vertical frequency : – with

epicycles cont. • using the circular frequency W, given by – so that disk galaxy: W ~ constant near centre – so k ~ 2 W • W ~ declines with R, Vrot » slower than Keplerian R-3/2 » lower limit is k ~ W in general W < k < 2 W R

Example: Oort’s constants near Sun – where R 0 is the galacto-centric distance • then k 2 = -4 A(A-B) + 4(A-B)2 = -4 B(A-B) = -4 BW 0 • Obs. A = 14. 5 km/s /kpc and B=-12 km/s /kpc

the sun makes 1. 3 oscillations in the radial direction per azimuthal (2 p) orbit – epicyclic approximation not valid for z-motions when |z|>300 pc

General Jeans Equations • CBE of the phase space density f is eq. of 7 variables and hence generally difficult to solve • Gain insights by taking moments of the CBE • where integrate over all possible velocities – U=1, vjvk

1 st Jeans (continuity) equation • define spatial density of stars n(x) • and the mean stellar velocity v(x) • then our zeroth moment equation becomes

3 rd Jeans Equation similar to the Euler equation for a fluid flow: – last term of RHS represents pressure force

JEANS EQUATION for oblate rotator : a steady-state axisymmetrical system in which ASSUME ij 2 is isotropic and the only streaming motion is azimuthal rotation:

• The velocity dispersions in this case are given by: • If we know the forms of (R, z) and (R, z) then at any radius R we may integrate the Jeans equation in the z direction to obtain 2.

Obtaining 2 Inserting this into the jeans equation in the R direction gives:

th 20 • orbits Lec

Applications of the Jeans Equations • I. The mass density in the solar neighbourhood • Using velocity and density distribution perpendicular to the Galactic disc – cylindrical coordinates. – Ignore R dependence

E. g. : Total Mass of spherical Milky WAY • Motions of globular clusters and satellite galaxies around 100 kpc of MW – Need n(r), vr 2, b to find M(r), including dark halo • Several attempts all suffer from problem of small numbers N ~ 15 • For the isotropic case, Little and Tremaine TOTAL mass of 2. 4 (+1. 3, -0, 7) 1011 Msol • 3 times the disc need DM

Power-law model of Milky Way • Isotropic orbits: • Radial orbits • If we assume a power law for the density distribution – E. g. Flat rotation a=1, Self-grav gamma=2, Radial anis. b >0. – E. g. , Point mass a=0, Tracer gamma=3. 5, Isotro b=0

Mass of the Milky Way: point-mass potential model We find

Vertical Jeans equation • Small z/R in the solar neighbourhood, R~8. 5 kpc, |z|< 1 kpc, R-dependence neglected. • Hence, reduces to vertical hydrostatic eq. :
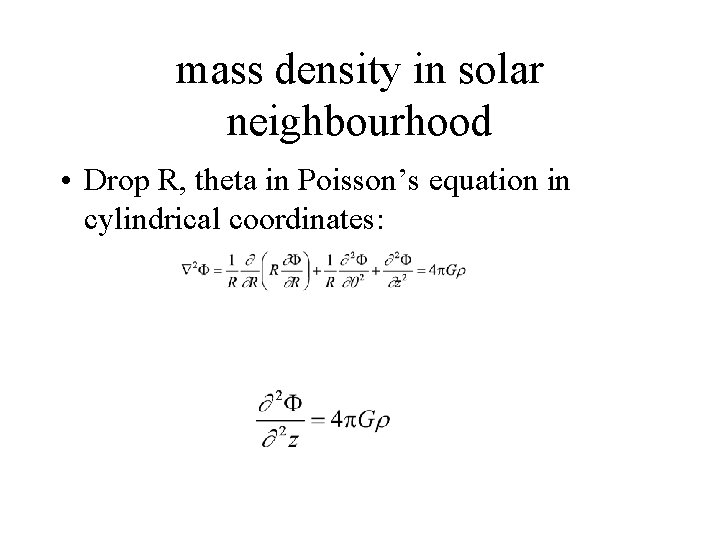
mass density in solar neighbourhood • Drop R, theta in Poisson’s equation in cylindrical coordinates:

local mass density = 0 Finally • all quantities on the LHS are, in principle, determinable from observations. RHS Known as the Oort limit. • Uncertain due to double differentiation!

local mass density • Don’t need to calculate for all stars – just a well defined population (ie G stars, BDs etc) – test particles (don’t need all the mass to test potential) • Procedure – determine the number density n, and the mean square vertical velocity, vz 2, the variance of the square of the velocity dispersion in the solar neighbourhood.

local mass density • > 1000 stars required • Oort : 0 = 0. 15 Msol pc-3 • K dwarf stars (Kuijken and Gilmore 1989) – MNRAS 239, 651 • Dynamical mass density of 0 = 0. 11 Msol pc -3 • also done with F stars (Knude 1994)

• Observed mass density of stars plus interstellar gas within a 20 pc radius is 0 = 0. 10 Msol pc-3 • can get better estimate of surface density • out to 700 pc S ~ 90 Msol pc-2 • from rotation curve Srot ~ 200 Msol pc-2

• Question 5:

Helpful Math/Approximations (To be shown at AS 4021 exam) • Convenient Units • Gravitational Constant • Laplacian operator in various coordinates • Phase Space Density f(x, v) relation with the mass in a small position cube and velocity cube

th 21 • orbits Lec: MOND
 Scoreboard architecture
Scoreboard architecture 11th chemistry thermodynamics lec 13
11th chemistry thermodynamics lec 13 Lec ditto
Lec ditto Lec scoreboard
Lec scoreboard Componentes del lec
Componentes del lec 11th chemistry thermodynamics lec 10
11th chemistry thermodynamics lec 10 Lec elements
Lec elements August lec 250
August lec 250 Underground pipeline irrigation system
Underground pipeline irrigation system Lec 1
Lec 1 Apelacin
Apelacin Lec
Lec 132000 lec
132000 lec Xrl in 8051
Xrl in 8051 Tipos de lec
Tipos de lec Sekisui s-lec america llc
Sekisui s-lec america llc 416 lec
416 lec Lec
Lec Brayton
Brayton Lec promotion
Lec promotion Lec anatomia
Lec anatomia History of software development life cycle
History of software development life cycle Xyloprin
Xyloprin Lec barbate
Lec barbate Lec hardver
Lec hardver Lec renal
Lec renal 252 lec
252 lec Normal phase vs reverse phase chromatography
Normal phase vs reverse phase chromatography M tswett pronunciation
M tswett pronunciation Mobile phase and stationary phase
Mobile phase and stationary phase Column chromatography images
Column chromatography images Normal phase vs reverse phase chromatography
Normal phase vs reverse phase chromatography Line vs phase voltage
Line vs phase voltage Detectors used in hplc
Detectors used in hplc In a ∆-connected source feeding a y-connected load
In a ∆-connected source feeding a y-connected load Csce 441
Csce 441 Phase space
Phase space Phase space
Phase space Phase space
Phase space Design systems
Design systems This is the final task in phase 3: systems design
This is the final task in phase 3: systems design Four phase power
Four phase power This is the final task in phase 3: systems design.
This is the final task in phase 3: systems design. This is the final task in phase 3 systems design
This is the final task in phase 3 systems design Cartesian space trajectory planning
Cartesian space trajectory planning Space junk the space age began
Space junk the space age began Camera space to world space
Camera space to world space Unscented trajectory chapter 5
Unscented trajectory chapter 5 World space to screen space
World space to screen space Nx space systems thermal
Nx space systems thermal Trl space systems
Trl space systems Atk space systems
Atk space systems Consultative committee for space data systems
Consultative committee for space data systems Ngsis
Ngsis Decision support systems and intelligent systems
Decision support systems and intelligent systems Principles of complex systems for systems engineering
Principles of complex systems for systems engineering Embedded systems vs cyber physical systems
Embedded systems vs cyber physical systems Elegant systems
Elegant systems Concentric winding diagram
Concentric winding diagram Sample atkins diet phase 1
Sample atkins diet phase 1 Phase contrast microscopy advantages
Phase contrast microscopy advantages Contrat de phase
Contrat de phase Neptune uranus
Neptune uranus Equillibria
Equillibria What is true labor
What is true labor Up unified process
Up unified process Data collection planning in the measure phase starts with
Data collection planning in the measure phase starts with Two basic properties of the gas phase are
Two basic properties of the gas phase are Phases of dental treatment planning
Phases of dental treatment planning Hrze dose
Hrze dose Phase 2 plumbing
Phase 2 plumbing Line vs phase voltage
Line vs phase voltage Line current and phase current
Line current and phase current Synchronous speed of motor
Synchronous speed of motor Goals and expected outcomes
Goals and expected outcomes Phase change formula
Phase change formula Gibbs phase rule
Gibbs phase rule Contoh visioning adalah
Contoh visioning adalah Tableau ero
Tableau ero Red giant phase
Red giant phase The two phase simplex method
The two phase simplex method Stability diagrams module
Stability diagrams module Mg al phase diagram
Mg al phase diagram Cded diet recipes
Cded diet recipes What is charted on an hr diagram
What is charted on an hr diagram Receptive relaxation
Receptive relaxation