CS 380 Computer Graphics Screen Space World Space

CS 380: Computer Graphics Screen Space & World Space Sung-Eui Yoon (윤성의) Course URL: http: //sglab. kaist. ac. kr/~sungeui/CG

Class Objectives ● Understand different spaces and basic Open. GL commands ● Understand a continuous world, Julia sets 2

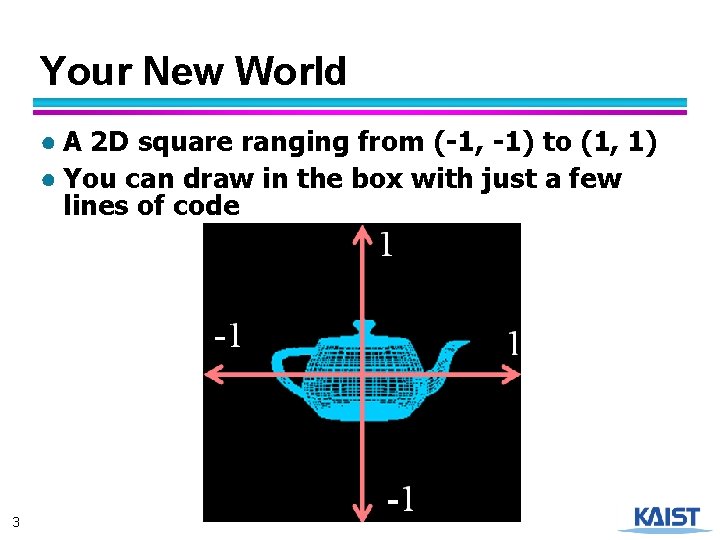
Your New World ● A 2 D square ranging from (-1, -1) to (1, 1) ● You can draw in the box with just a few lines of code 3

Code Example (Immediate Mode) Legacy Open. GL code: gl. Color 3 d(0. 0, 0. 8, 1. 0); gl. Begin(GL_POLYGON); gl. Vertex 2 d(-0. 5, -0. 5); gl. Vertex 2 d( 0. 5, 0. 5); gl. Vertex 2 d(-0. 5, 0. 5); gl. End(); 4

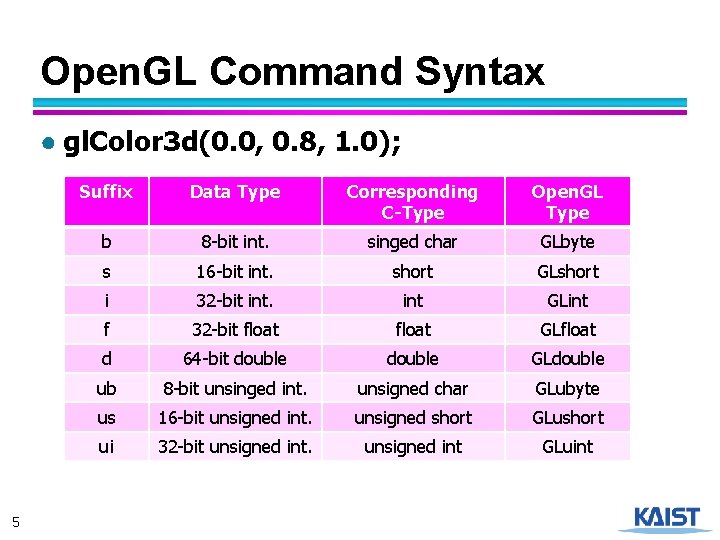
Open. GL Command Syntax ● gl. Color 3 d(0. 0, 0. 8, 1. 0); 5 Suffix Data Type Corresponding C-Type Open. GL Type b 8 -bit int. singed char GLbyte s 16 -bit int. short GLshort i 32 -bit int GLint f 32 -bit float GLfloat d 64 -bit double GLdouble ub 8 -bit unsinged int. unsigned char GLubyte us 16 -bit unsigned int. unsigned short GLushort ui 32 -bit unsigned int GLuint

Open. GL Command Syntax ● You can use pointers or buffers gl. Color 3 f(0. 0, 0. 8, 1. 0); GLfloat color_array [] = {0. 0, 0. 8, 1. 0}; gl. Color 3 fv (color_array); ● Using buffers for drawing is much more efficient 6

Another Code Example Open. GL Code: gl. Color 3 d(0. 0, 0. 8, 1. 0); gl. Begin(GL_POLYGON); gl. Vertex 2 d(-0. 5, -0. 5); gl. Vertex 2 d( 0. 5, gl. End() 7 0. 5);

Drawing Primitives in Open. GL 8 The red book

Yet Another Code Example Open. GL Code: gl. Color 3 d(0. 8, 0. 6, 0. 8); gl. Begin(GL_LINE_LOOP); for (i = 0; i < 360; i = i + 2) { x = cos(i*pi/180); y = sin(i*pi/180); gl. Vertex 2 d(x, y); } gl. End(); 9

Open. GL as a State Machine ● Open. GL maintains various states until you change them // set the current color state gl. Color 3 d(0. 0, 0. 8, 1. 0); gl. Begin(GL_POLYGON); gl. Vertex 2 d(-0. 5, -0. 5); gl. Vertex 2 d( 0. 5, 0. 5); gl. End() 10

Open. GL as a State Machine ● Open. GL maintains various states until you change them ● Many state variables refer to modes (e. g. , lighting mode) ● You can enable, gl. Enable (), or disable, gl. Disable () ● You can query state variables ● gl. Get. Floatv (), gl. Is. Enabled (), etc. ● gl. Get. Error (): very useful for debugging 11

Debugging Tip #define Check. Error(s) { GLenum error = gl. Get. Error(); if (error) printf("%s in %sn", glu. Error. String(error), s); } gl. Tex. Coord. Pointer (2, x, sizeof(y), (GLvoid *) Tex. Delta); Check. Error ("Tex Bind"); gl. Draw. Elements(GL_TRIANGLES, x, GL_UNSIGNED_SHORT, 0); Check. Error ("Tex Draw"); 12

Open. GL Ver. 4. 3 (Using Retained Mode) #include <iostream> using namespace std; #include "vgl. h" #include "Load. Shaders. h" enum VAO_IDs { Triangles, Num. VAOs }; enum Buffer_IDs { Array. Buffer, Num. Buffers }; enum Attrib_IDs { v. Position = 0 }; GLuint VAOs[Num. VAOs]; GLuint Buffers[Num. Buffers]; const GLuint Num. Vertices = 6; Shader. Info shaders[] = { { GL_VERTEX_SHADER, "triangles. vert" }, { GL_FRAGMENT_SHADER, "triangles. frag" }, { GL_NONE, NULL } }; GLuint program = Load. Shaders(shaders); gl. Use. Program(program); gl. Vertex. Attrib. Pointer(v. Position, 2, GL_FLOAT, GL_FALSE, 0, BUFFER_OFFSET(0)); gl. Enable. Vertex. Attrib. Array(v. Position); } Void display(void) { gl. Clear(GL_COLOR_BUFFER_BIT); gl. Bind. Vertex. Array(VAOs[Triangles]); gl. Draw. Arrays(GL_TRIANGLES, 0, Num. Vertices); gl. Flush(); } Int main(int argc, char** argv) { glut. Init(&argc, argv); glut. Init. Display. Mode(GLUT_RGBA); glut. Init. Window. Size(512, 512); glut. Init. Context. Version(4, 3); glut. Init. Context. Profile(GLUT_CORE_PROFILE); glut. Create. Window(argv[0]); gl. Bind. Buffer(GL_ARRAY_BUFFER, Buffers[Array. Buffer]); if (glew. Init()) { exit(EXIT_FAILURE); } gl. Buffer. Data(GL_ARRAY_BUFFER, sizeof(vertices), init(); glut. Display. Func(display); glut. Main. Loop(); vertices, GL_STATIC_DRAW); } 13 Void init(void) { gl. Gen. Vertex. Arrays(Num. VAOs, VAOs); gl. Bind. Vertex. Array(VAOs[Triangles]); GLfloat vertices[Num. Vertices][2] = { { -0. 90, -0. 90 }, // Triangle 1 { 0. 85, -0. 90 }, { -0. 90, 0. 85 }, { 0. 90, -0. 85 }, // Triangle 2 { 0. 90, 0. 90 }, { -0. 85, 0. 90 } }; gl. Gen. Buffers(Num. Buffers, Buffers);

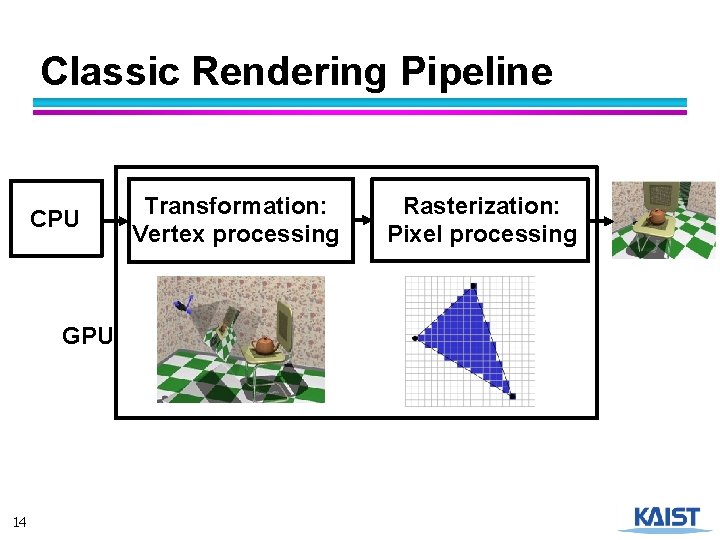
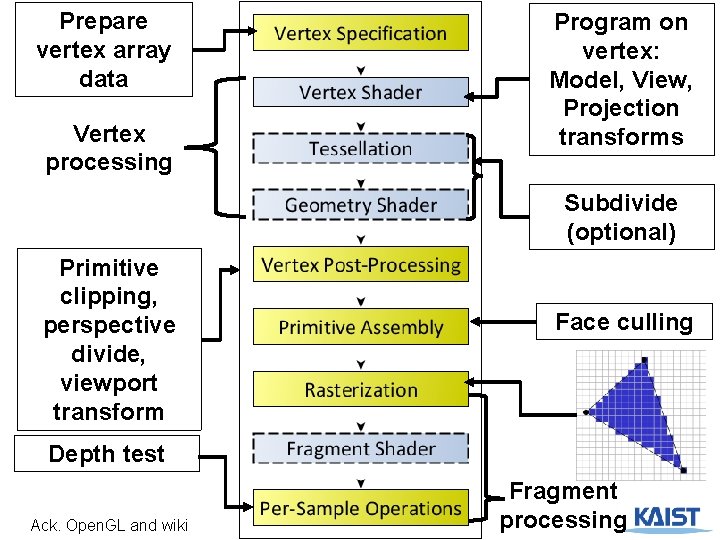
Classic Rendering Pipeline CPU GPU 14 Transformation: Vertex processing Rasterization: Pixel processing

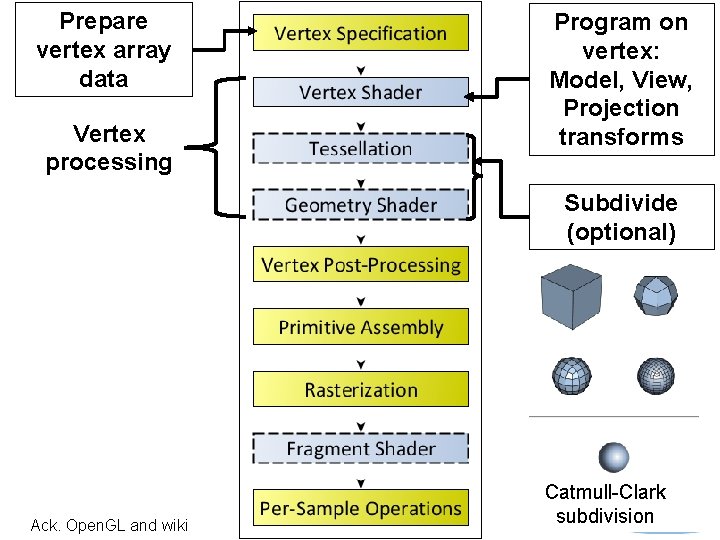
Prepare vertex array data Vertex processing Program on vertex: Model, View, Projection transforms Subdivide (optional) 15 Ack. Open. GL and wiki Catmull-Clark subdivision

Prepare vertex array data Vertex processing Program on vertex: Model, View, Projection transforms Subdivide (optional) Primitive clipping, perspective divide, viewport transform Face culling Depth test 16 Ack. Open. GL and wiki Fragment processing

Julia Sets (Fractal) ● Study a visualization of a simple iterative function defined over the imaginary plane ● It has chaotic behavior ● Small changes have dramatic effects Demo 17

Julia Set - Definition ● The Julia set Jc for a number c in the complex plane P is given by: Jc = { p | p P and pi+1 = p 2 i + c converges to a fixed limit } 18

Complex Numbers ● Consists of 2 tuples (Real, Imaginary) ● E. g. , c = a + bi ● Various operations ● ● 19 c 1 + c 2 = (a 1 + a 2) + (b 1 + b 2)i c 1 c 2 = (a 1 a 2 - b 1 b 2) + (a 1 b 2 + a 2 b 1)i (c 1)2 = ((a 1)2 – (b 1)2) + (2 a 1 b 1)i |c| = sqrt(a 2 + b 2)

Convergence Example ● Real numbers are a subset of complex numbers: ● Consider c = [0, 0], and p = [x, 0] ● For what values of x is xi+1 = xi 2 convergent? How about x 0 = 0. 5? x 0 -4 = 0. 5, 0. 25, 0. 0625, 0. 0039 20

Convergence Example ● Real numbers are a subset of complex numbers: ● consider c = [0, 0], and p = [x, 0] ● for what values of x is xi+1 = xi 2 convergent? How about x 0 = 1. 1? x 0 -4 = 1. 1, 1. 21, 1. 4641, 2. 14358 0 21 1

Convergence Properties ● Suppose c = [0, 0], for what complex values of p does the series converge? ● For real numbers: ● If |xi| > 1, then the series diverges ● For complex numbers ● If |pi| > 2, then the series diverges ● Loose bound Imaginary part 22 The black points are the ones in Julia set Real part

A Peek at the Fractal Code class Complex { float re, im; }; viod Julia (Complex p, Complex c, int & i, float & r) { int max. Iterations = 256; for (i = 0; i < max. Iterations; i++) { p = p*p + c; i & r are used to r. Sqr = p. re*p. re + p. im*p. im; assign a color if( r. Sqr > 4 ) break; } r = sqrt(r. Sqr); 23 }

How can we see more? ● Our world view allows us to see so much ● What if we want to zoom in? ● We need to define a mapping from our desired world view to our screen 24

Mapping from World to Screen Camera World 25 Window Monitor Screen

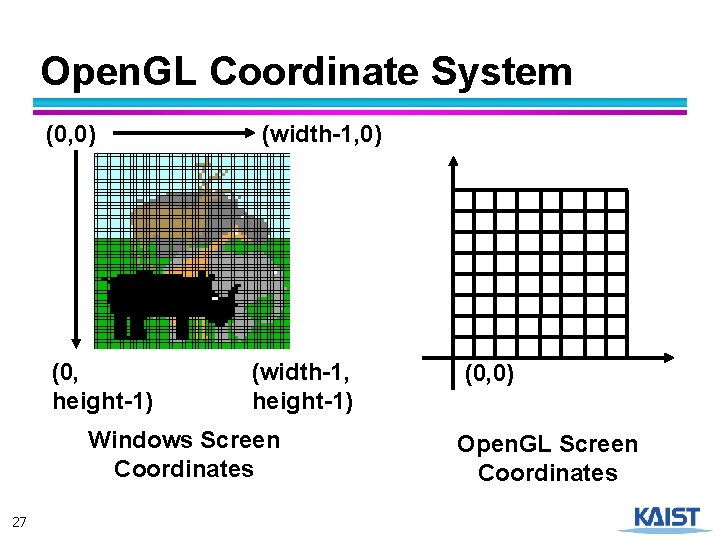
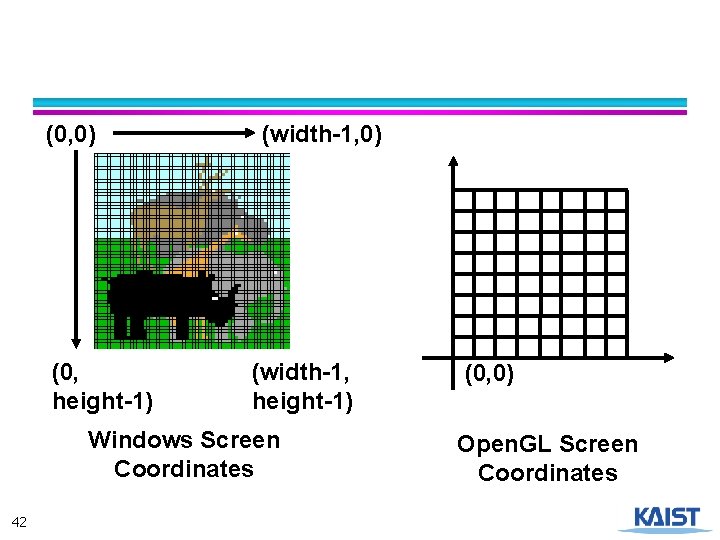
Screen Space ● Graphical image is presented by setting colors for a set of discrete samples called “pixels” (0, 0) (width-1, 0) ● Pixels displayed on screen in windows ● Pixels are addressed as 2 D arrays ● Indices are “screenspace” coordinates (0, height-1) 26 (width-1, height-1)

Open. GL Coordinate System (0, 0) (0, height-1) (width-1, 0) (width-1, height-1) Windows Screen Coordinates 27 (0, 0) Open. GL Screen Coordinates

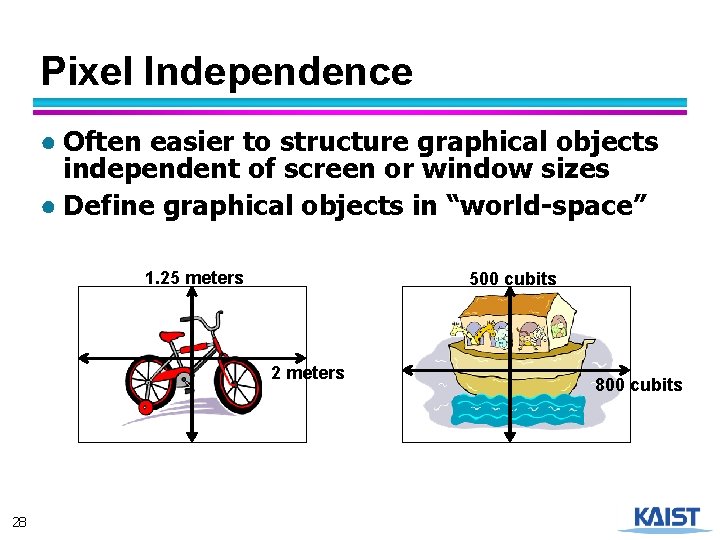
Pixel Independence ● Often easier to structure graphical objects independent of screen or window sizes ● Define graphical objects in “world-space” 1. 25 meters 500 cubits 2 meters 28 800 cubits

Normalized Device Coordinates ● Intermediate “rendering-space” ● Compose world and screen space ● Sometimes called “canonical screen space” 1 -1 29

Why Introduce NDC? ● Simplifies many rendering operations ● Clipping, computing coefficients for interpolation ● Separates the bulk of geometric processing from the specifics of rasterization (sampling) ● Will be discussed later 30

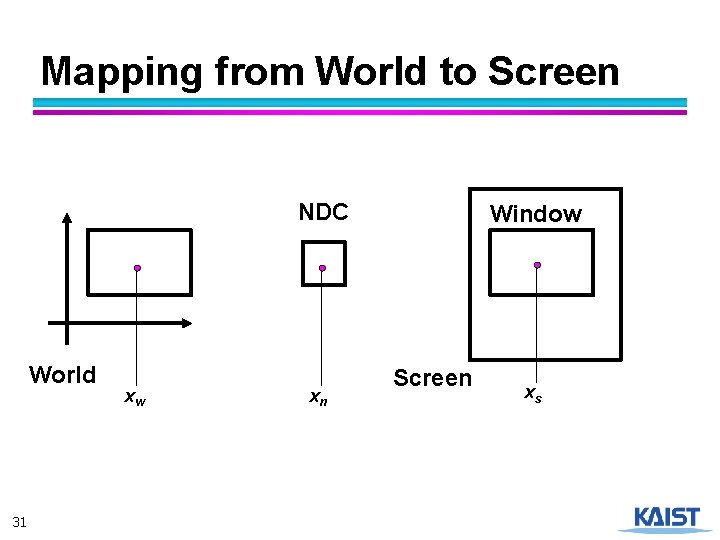
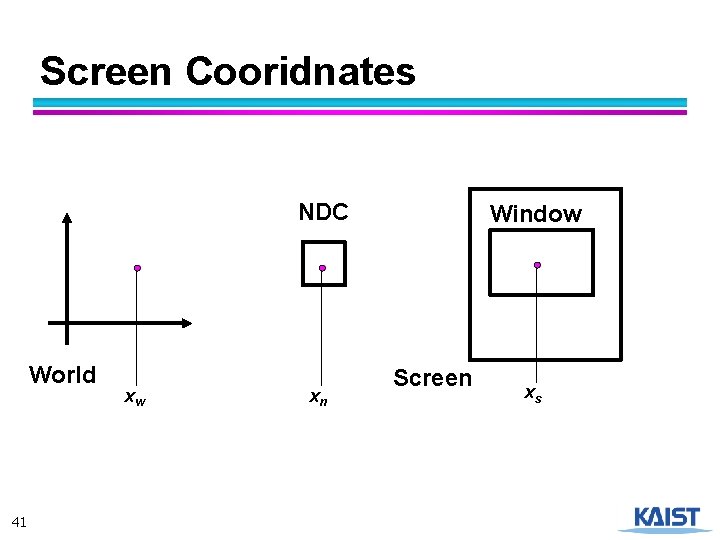
Mapping from World to Screen NDC World 31 xw xn Window Screen xs

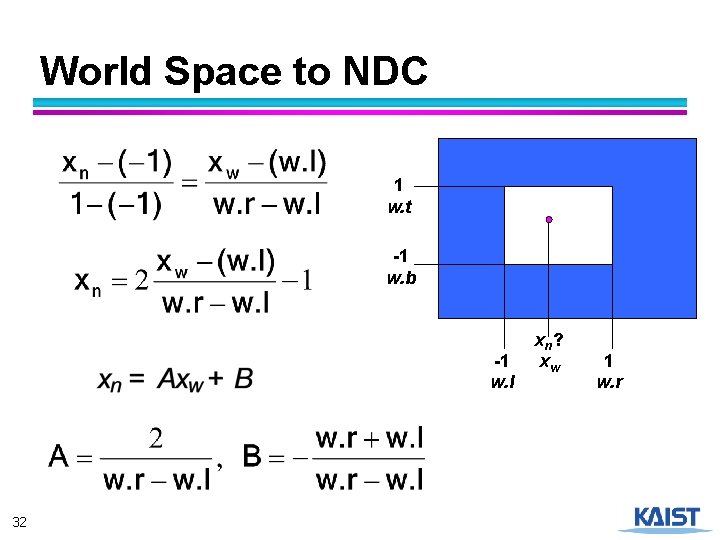
World Space to NDC 1 w. t -1 w. b -1 w. l 32 xn? xw 1 w. r

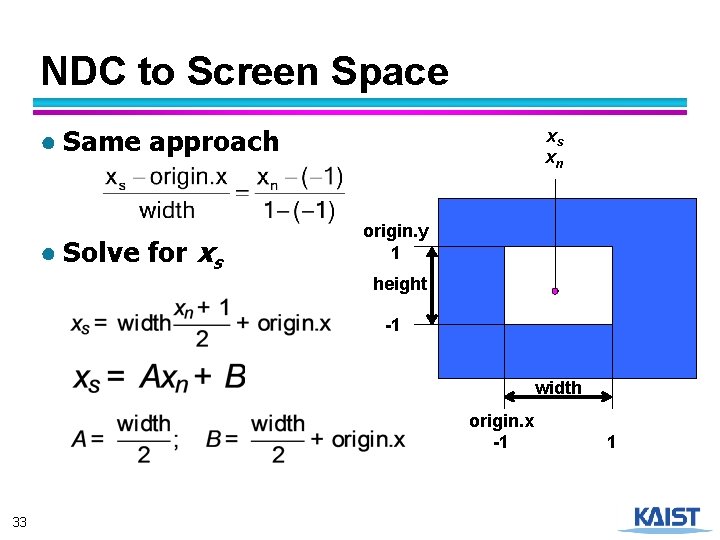
NDC to Screen Space ● Same approach ● Solve for xs xs xn origin. y 1 height -1 width origin. x -1 33 1

Class Objectives were: ● Understand different spaces and basic Open. GL commands ● Understand a continuous world, Julia sets 34

Any Questions? ● Come up with one question on what we have discussed in the class and submit at the end of the class ● 1 for already answered questions ● 2 for typical questions ● 3 for questions with thoughts or that surprised me ● Submit at least four times during the whole semester 35 ● Multiple questions in one time are counted as once

Homework ● Go over the next lecture slides before the class ● Watch 2 SIGGRAPH videos and submit your summaries before every Tue. class ● Send an email to cs 380 ta@gmail. com ● Just one paragraph for each summary Example: Title: XXXX Abstract: this video is about accelerating the performance of ray tracing. To achieve its goal, they design a new technique for reordering rays, since by doing so, they can improve the ray coherence and thus improve the overall performance. 36

Homework for Next Class ● Read Chapter 1, Introduction ● Read “Numerical issues” carefully 37

Next Time ● Basic Open. GL program structure and how Open. GL supports different spaces 38

Figs 39

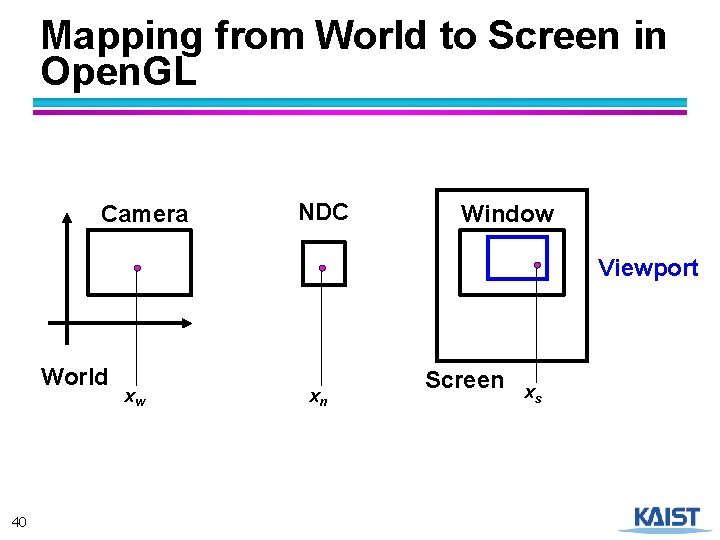
Mapping from World to Screen in Open. GL Camera NDC Window Viewport World 40 xw xn Screen xs

Screen Cooridnates NDC World 41 xw xn Window Screen xs

(0, 0) (0, height-1) (width-1, 0) (width-1, height-1) Windows Screen Coordinates 42 (0, 0) Open. GL Screen Coordinates