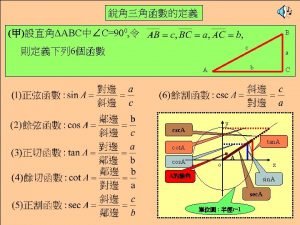
Exact Values Some special values of Sin Cos

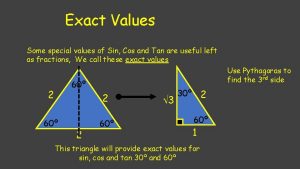
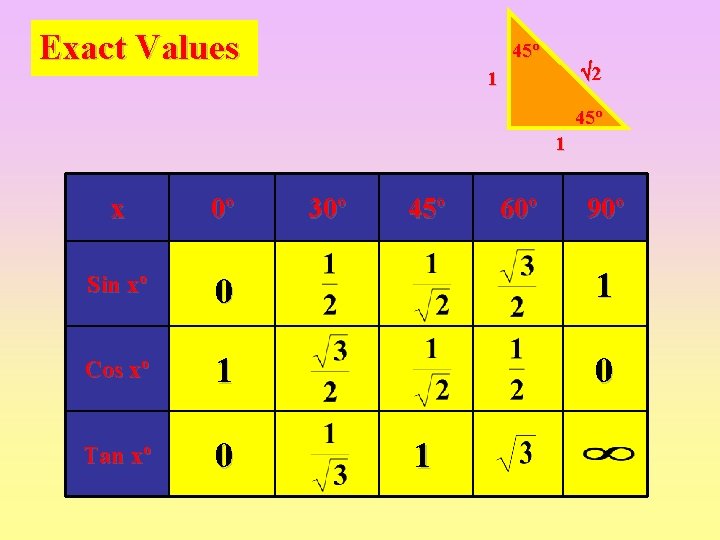
Exact Values Some special values of Sin, Cos and Tan are useful left as fractions, We call these exact values 60º 2 2 60º 3 30º 2 This triangle will provide exact values for sin, cos and tan 30º and 60º 2 60º 1

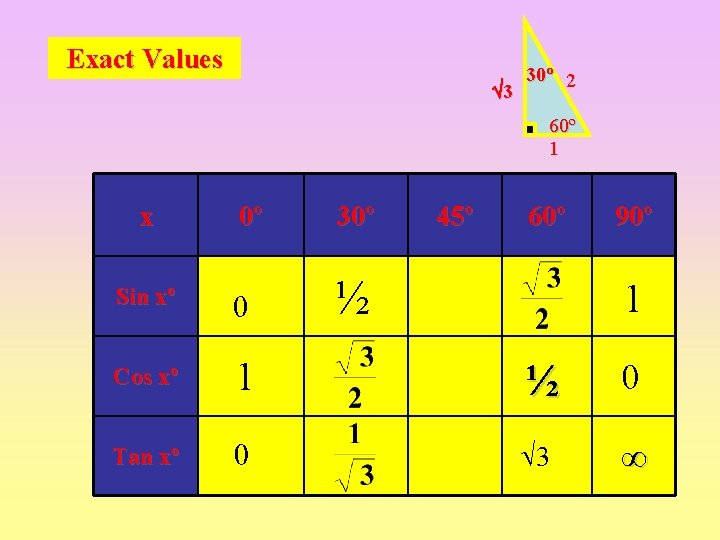
Exact Values 3 30º 2 60º 1 x 0º 30º 45º 60º 90º Sin xº 0 ½ Cos xº 1 ½ 0 Tan xº 0 3 ∞ 1

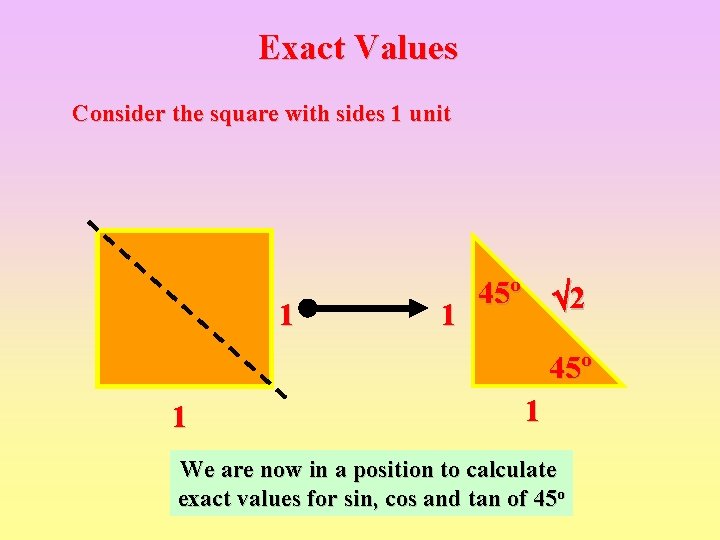
Exact Values Consider the square with sides 1 unit 1 45º 2 1 45º 1 1 We are now in a position to calculate exact values for sin, cos and tan of 45 o

Exact Values 45º 2 1 45º 1 x 0º 30º 45º Sin xº 0 1 Cos xº 1 0 Tan xº 0 1 60º 90º

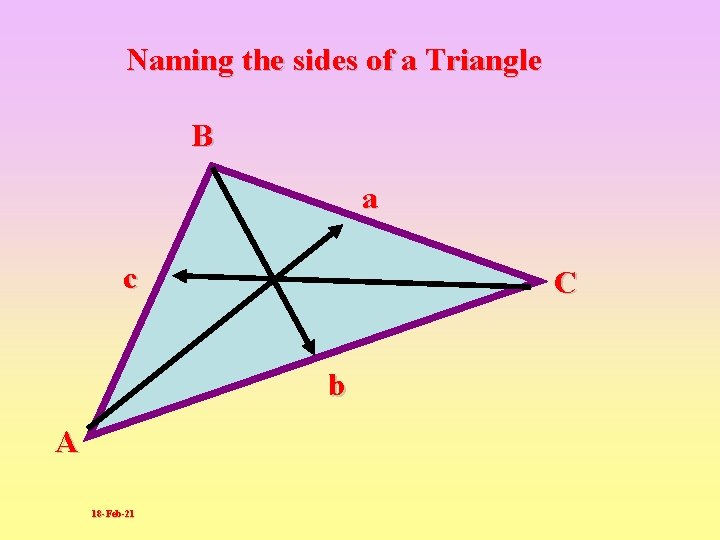
Naming the sides of a Triangle B a c C b A 18 -Feb-21

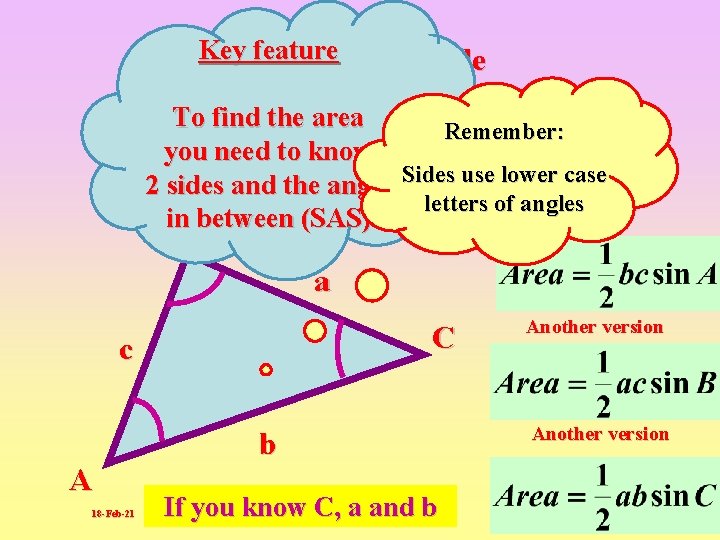
Key feature Area of ANY Triangle To find the area Remember: you need to know The area of ANY triangle can be found Sides use lower case 2 sides and the angle by the following letters formula. of angles in between (SAS) B a C c A 18 -Feb-21 b If A, B, ab and c If you know C, and b Another version

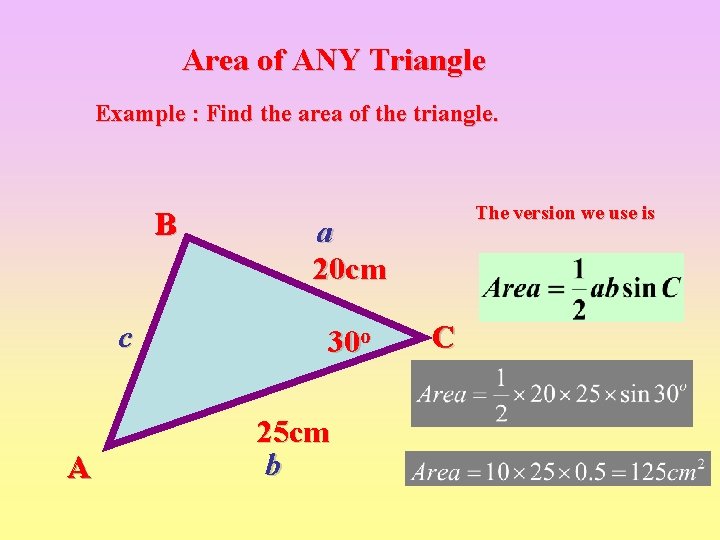
Area of ANY Triangle Example : Find the area of the triangle. B c A The version we use is a 20 cm 30 o 25 cm b C

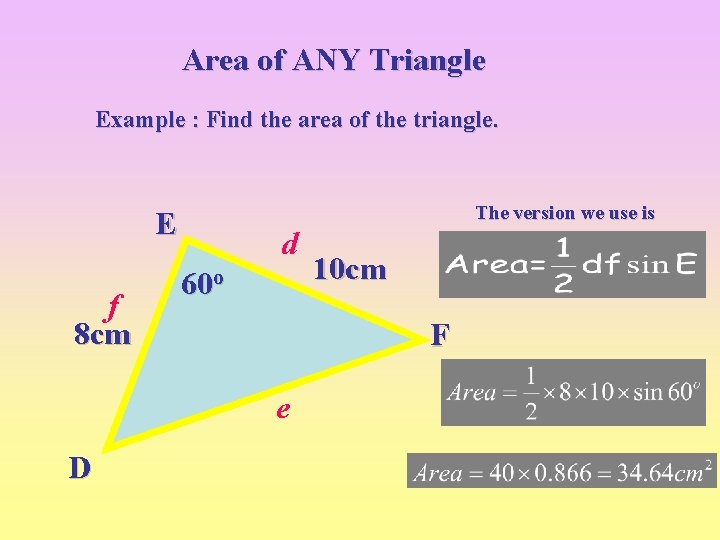
Area of ANY Triangle Example : Find the area of the triangle. The version we use is E f 8 cm d 60 o F e D 10 cm

Key feature What Goes In The Box ? Remember Calculate the areas of the triangles below: (SAS) (1) 12. 6 cm A =36. 9 cm 2 23 o 15 cm (2) 5. 7 m 71 o 6. 2 m A =16. 7 m 2

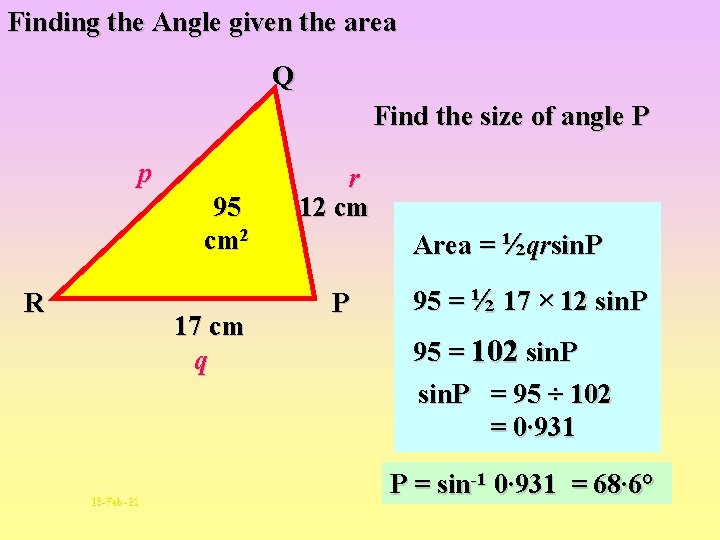
Finding the Angle given the area Q Find the size of angle P p 95 cm 2 R 17 cm q 18 -Feb-21 r 12 cm Area = ½qrsin. P P 95 = ½ 17 × 12 sin. P 95 = 102 sin. P = 95 ÷ 102 = 0∙ 931 P = sin-1 0∙ 931 = 68∙ 6°

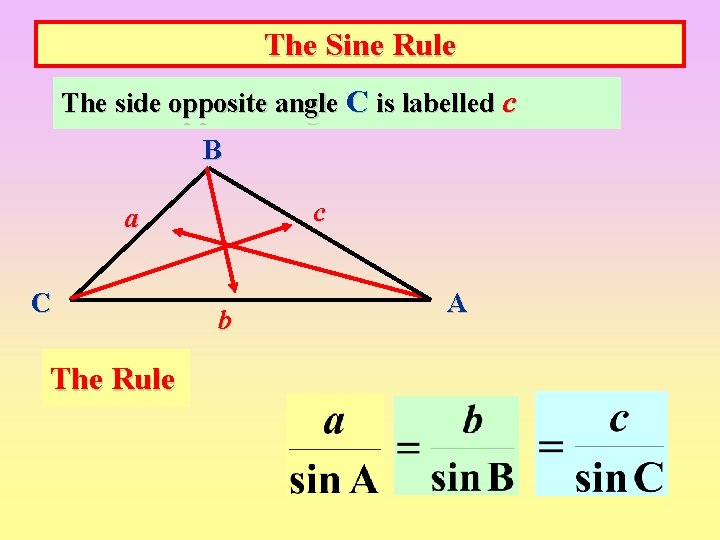
The Sine Rule The A is labelled b ca The side opposite angle C B is B c a C The Rule b A

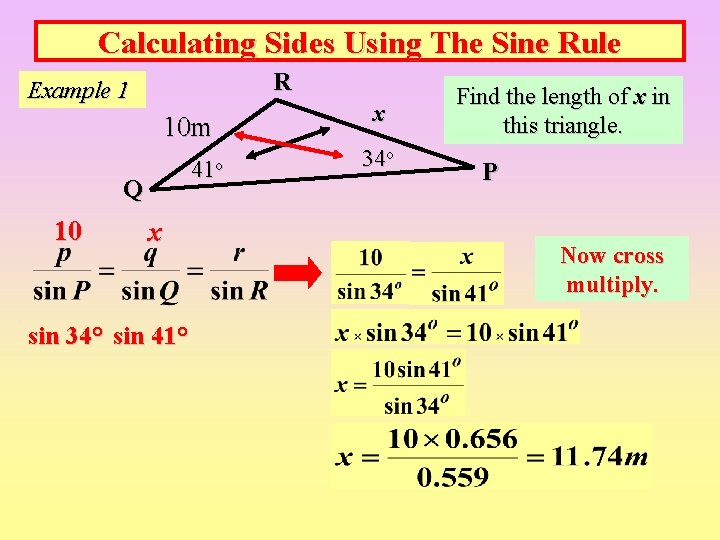
Calculating Sides Using The Sine Rule R Example 1 10 m 41 o Q 10 x sin 34° sin 41° x 34 o Find the length of x in this triangle. P Now cross multiply.

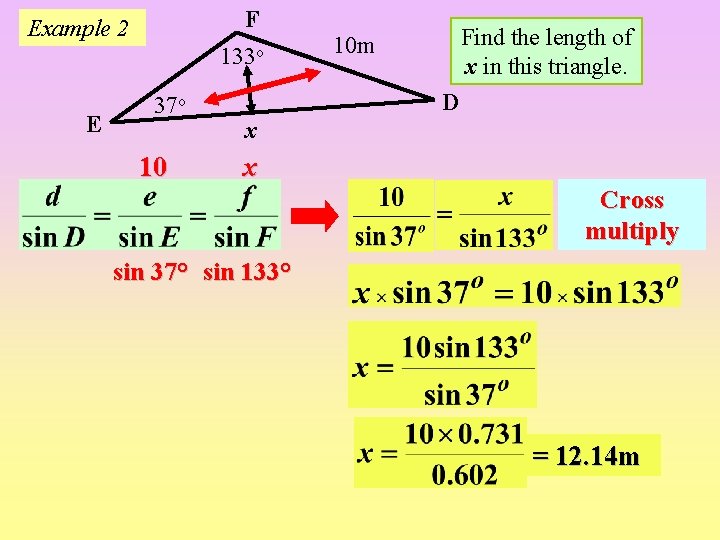
F Example 2 133 o E 37 o 10 Find the length of x in this triangle. 10 m D x x Cross multiply sin 37° sin 133° = 12. 14 m

Problem The balloon is anchored to the ground as shown in the diagram. Calculate the distance between the anchor points. x A 25 25 m 35° b c sin 35° sin 70° Cross multiply 75° B 70° xm C a

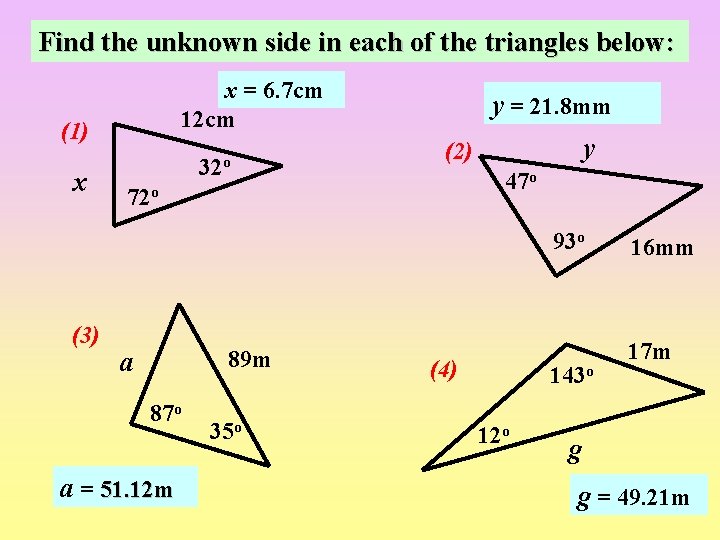
Find the unknown side in each of the triangles below: x = 6. 7 cm 12 cm (1) x 32 o y = 21. 8 mm y (2) 47 o 72 o 93 o (3) 89 m a 87 o a = 51. 12 m 35 o (4) 143 o 12 o 16 mm 17 m g g = 49. 21 m

Calculating Angles Using The Sine Rule Example 1. Y Find the angle ao 38 m ao 45 45 m 23 o Z X 38 Cross multiply sin aº sin 23º = 0. 463 Use sin-1

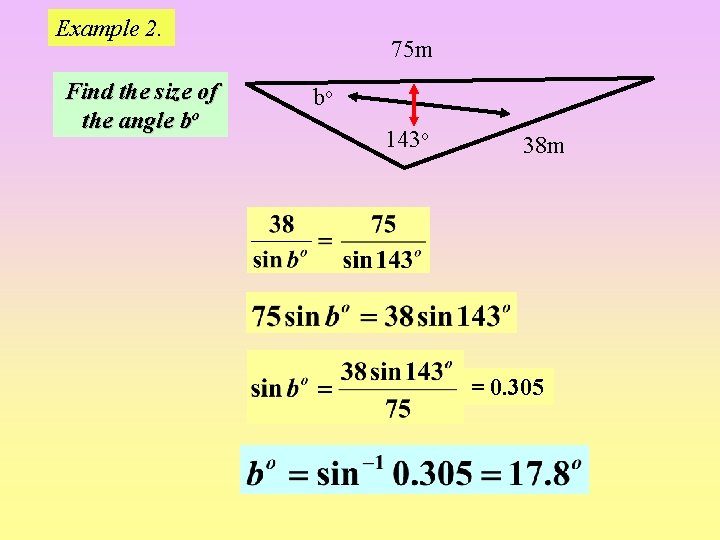
Example 2. Find the size of the angle bo 75 m bo 143 o 38 m = 0. 305

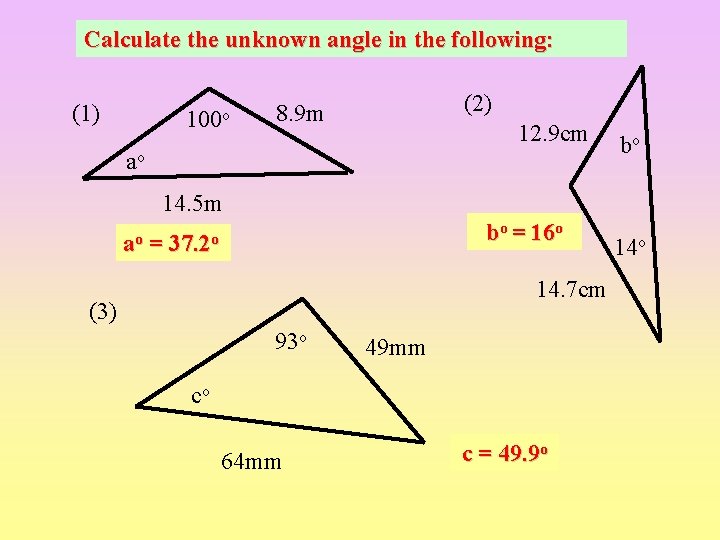
Calculate the unknown angle in the following: (1) 100 o (2) 8. 9 m 12. 9 cm ao bo 14. 5 m ao = bo = 16 o 37. 2 o 14. 7 cm (3) 93 o 49 mm co 64 mm c = 49. 9 o 14 o

Sine Rule Basic Examples

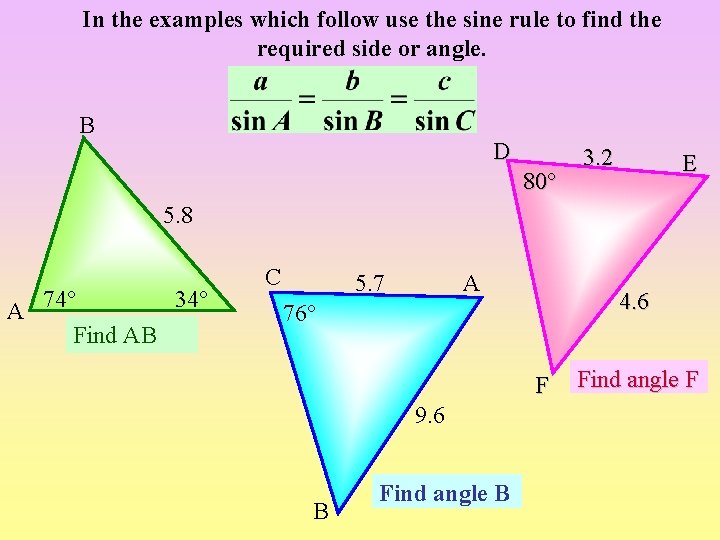
In the examples which follow use the sine rule to find the required side or angle. B D 80° 3. 2 E 5. 8 34° A 74° Find AB C 5. 7 A 4. 6 76° C F 9. 6 B Find angle F

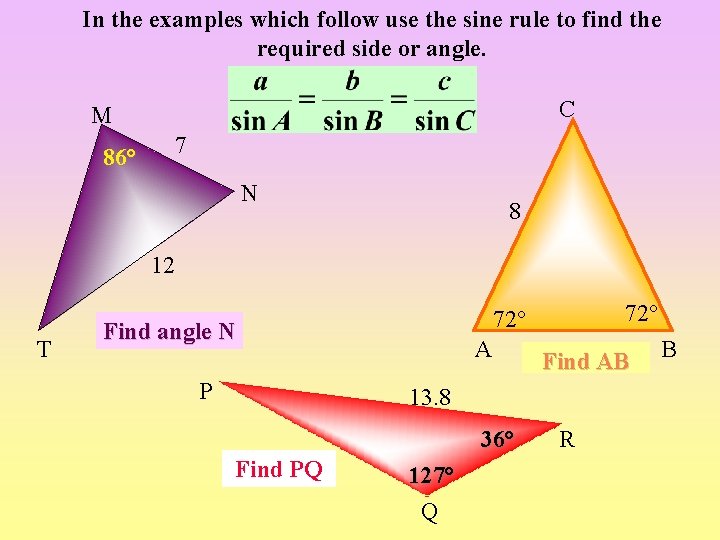
In the examples which follow use the sine rule to find the required side or angle. C M 7 86° N 8 12 T Find angle N P 72° A Find AB 13. 8 36° Find PQ 127° Q R B

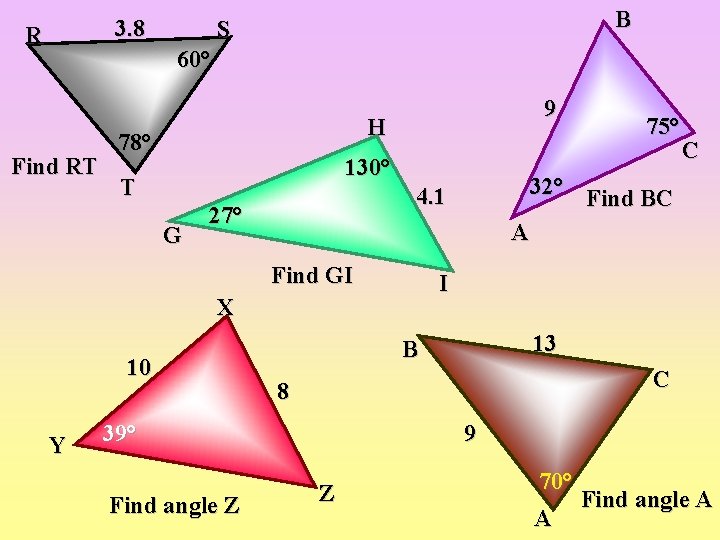
3. 8 R B S 60° Find RT 9 H 78° 130° T G A Find GI I X 10 Y 13 B C 8 39° Find angle Z C 32° Find BC 4. 1 27° 75° 9 Z 70° Find angle A A

Sine Rule (Bearings) Trigonometry

In the examples which follow use the sine rule to find the required side or angle. 1. Consider two radar stations Alpha and Beta. Alpha is 140 miles west of Beta. The bearing of an aero plane from Alpha is 032° and from Beta it is 316°. How far is the aeroplane from each of the radar stations?

2. Two ports Dundee and Stonehaven are 54 miles apart with Dundee approximately due south of Stonehaven. The bearing of a ship at sea from Stonehaven is 098° and from Dundee it is 048°. How far is the ship from Dundee? 3. A ship is sailing north. At noon its bearing from a lighthouse is 240°. Five hours later the ship is 84 km further north and its new bearing from the lighthouse is 290°. How far is the ship from the lighthouse now?

4. Two ports P and Q are 35 miles apart with P due east of Q. The bearings of a ship from P and Q are 190° and 126° respectively. a) What is the bearing of port Q from the ship? b) How far is the ship from port P 5. The bearing of an aeroplane from Aberdeen is 068° and from Dundee it is 030°. Dundee is 69 miles south of Aberdeen. How far is the aero plane from Aberdeen?

6. Two oil rigs are 80 miles apart with rig B being 80 miles east of rig A. The bearing of a ship from rig B is 194° and from A the bearing is 140°. Find the distance of the ship from rig A. 7. At noon a ship lies on a bearing 070° from Dundee. The ship sails a distance of 45 miles south and at 3 pm its new bearing from Dundee is 130°. How far is the ship from Dundee now? If the ship maintains the same speed, how long will it take to return to Dundee?

8. An aeroplane leaves Leuchers airport and flies 80 miles north. It then changes direction and flies 120 miles east. The plane now turns onto a bearing of 126° and flies a further 164 miles. Calculate the bearing and distance of the plane from Leuchers.

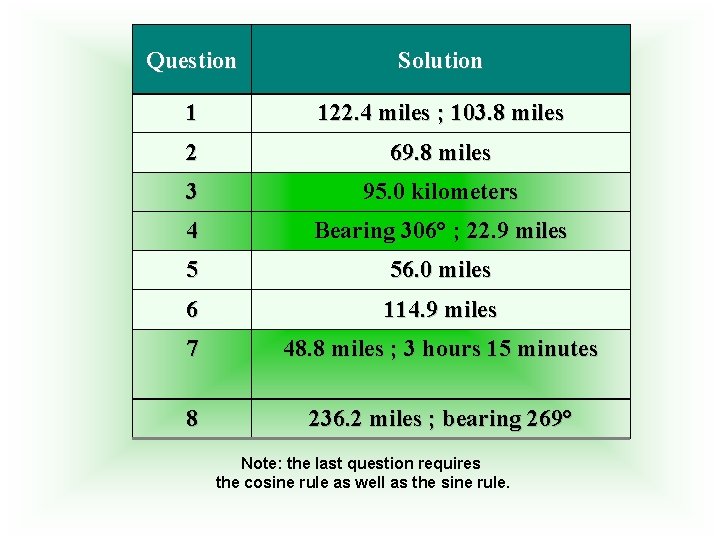
Question Solution 1 122. 4 miles ; 103. 8 miles 2 69. 8 miles 3 95. 0 kilometers 4 Bearing 306° ; 22. 9 miles 5 56. 0 miles 6 114. 9 miles 7 48. 8 miles ; 3 hours 15 minutes 8 236. 2 miles ; bearing 269° Note: the last question requires the cosine rule as well as the sine rule.

Cosine Rule The Cosine Rule can be used with ANY triangle as long as we have been given enough information B a c A 18 -Feb-21 C b Given angle C A B

Using The Cosine Rule Example 1 : Find the unknown side in the triangle below: C 5 m A x 43 o 12 m Identify sides a, b, c and angle Ao B a = x b = 5 c =12 Ao = 43 o Write down the Cosine Rule for a a 2 = b 2 + c 2 - 2 bc cos A x 2 = 52 + 122 - 2 x 5 x 12 cos 43 o x 2 = 81. 28 x = 9. 02 m Substitute values Square root to find “x”.

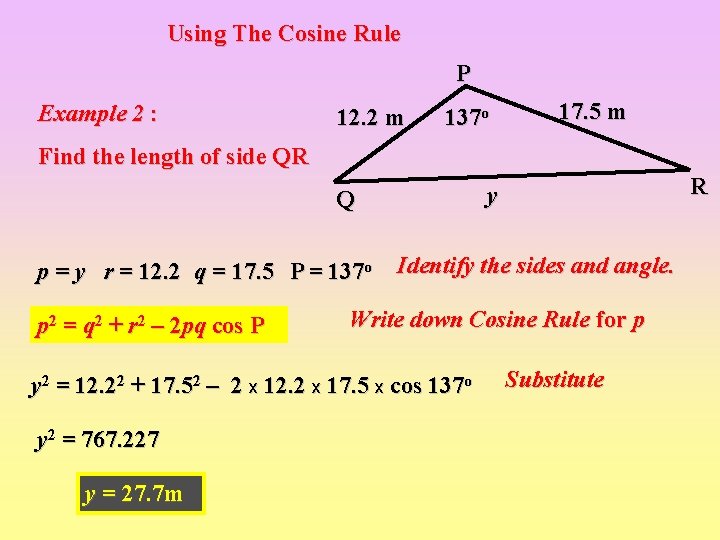
Using The Cosine Rule P Example 2 : 12. 2 m 137 o 17. 5 m Find the length of side QR p = y r = 12. 2 q = 17. 5 P = 137 o p 2 = q 2 + r 2 – 2 pq cos P Identify the sides and angle. Write down Cosine Rule for p y 2 = 12. 22 + 17. 52 – 2 x 12. 2 x 17. 5 x cos 137 o y 2 = 767. 227 y = 27. 7 m R y Q Substitute

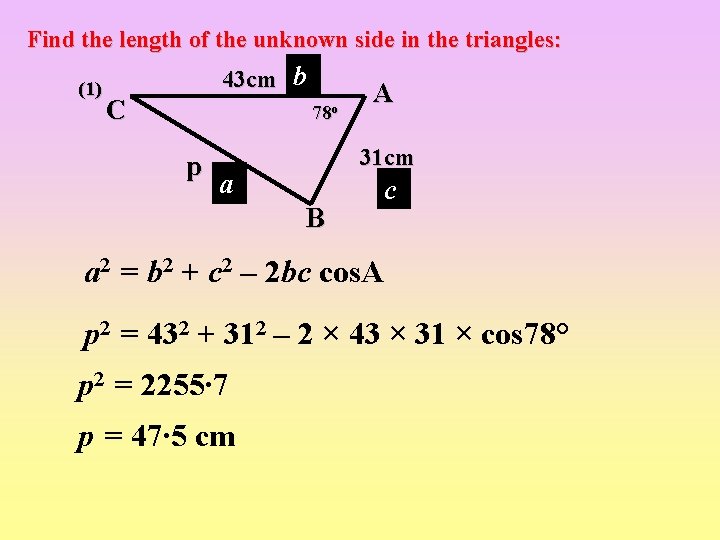
Find the length of the unknown side in the triangles: (1) 43 cm b C 78 o p A 31 cm a B c a 2 = b 2 + c 2 – 2 bc cos. A p 2 = 432 + 312 – 2 × 43 × 31 × cos 78° p 2 = 2255∙ 7 p = 47∙ 5 cm

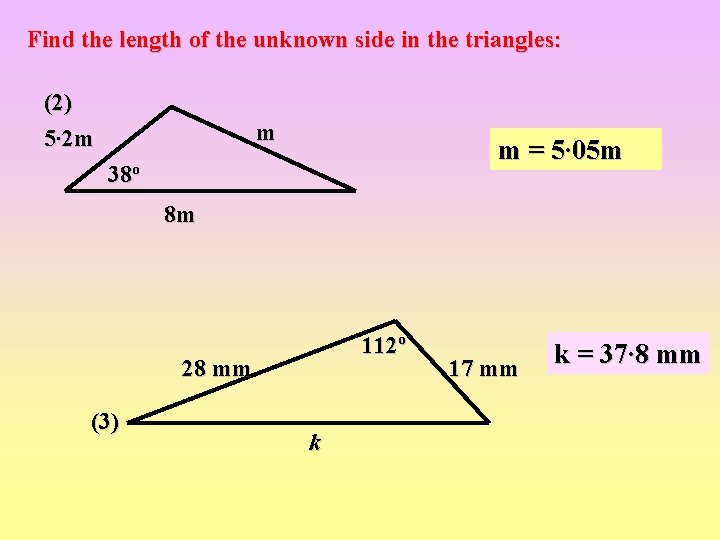
Find the length of the unknown side in the triangles: (2) 5∙ 2 m m m = 5∙ 05 m 38 o 8 m 112º 28 mm (3) k 17 mm k = 37∙ 8 mm

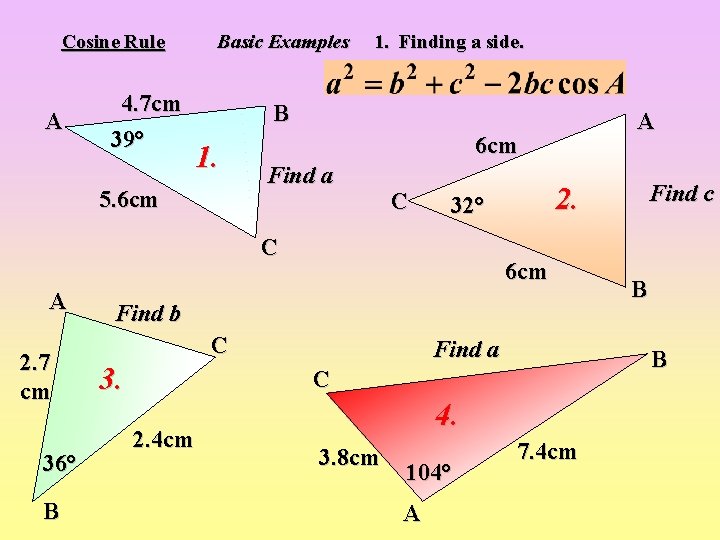
Cosine Rule A 4. 7 cm 39° Basic Examples 1. Finding a side. B 1. 5. 6 cm Find a C C 32° C A 2. 7 cm 36° B A 6 cm Find b C 3. Find a 4. 3. 8 cm 104° A B B C 2. 4 cm Find c 2. 7. 4 cm

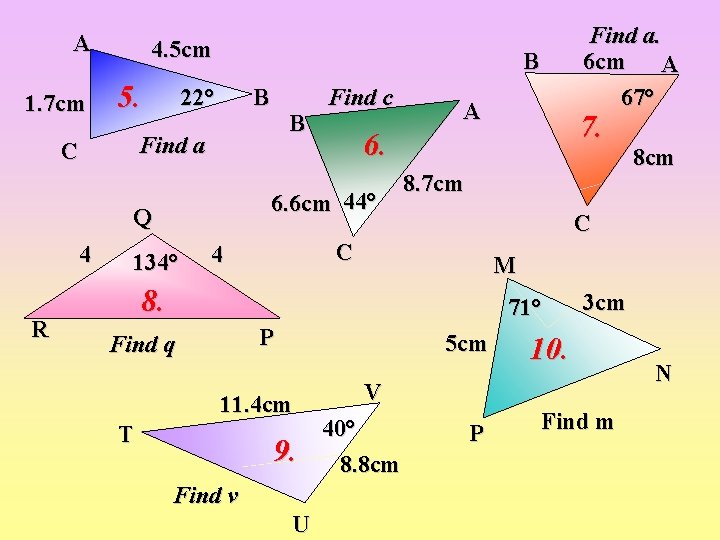
A 1. 7 cm 4. 5 cm 5. B 22° B R Find c 134° A 8. 7 cm M 8. 71° P Find q 5 cm 11. 4 cm T 9. Find v U 8 cm C C 4 7. 6. 6 cm 44° Q 4 B Find a C Find a. 6 cm A 67° 3 cm 10. V 40° 8. 8 cm P Find m N

Finding Angles Using The Cosine Rule formula can be rearranged to allow us to find the size of an angle This formula is cyclic, depending on the angle to be found

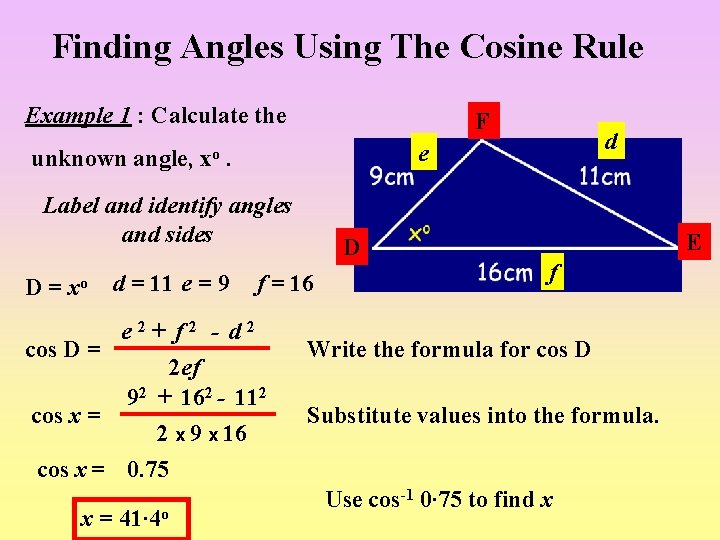
Finding Angles Using The Cosine Rule Example 1 : Calculate the unknown angle, xo F . Label and identify angles and sides D= xo d = 11 e = 9 D f = 16 e 2+ f 2 - d 2 cos D = 2 ef 92 + 162 - 112 cos x = 2 x 9 x 16 cos x = 0. 75 x = 41∙ 4 o d e E f Write the formula for cos D Substitute values into the formula. Use cos-1 0∙ 75 to find x

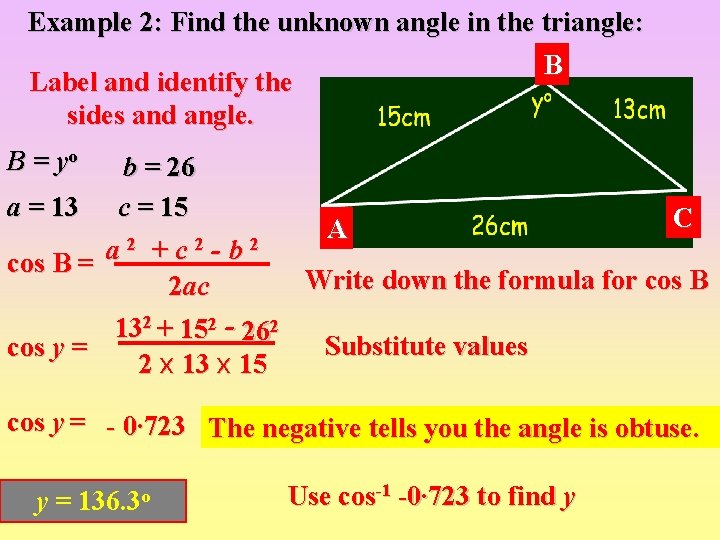
Example 2: Find the unknown angle in the triangle: Label and identify the sides and angle. B = yo a = 13 cos B = cos y = B b = 26 c = 15 C A a 2 +c 2 -b 2 Write down the formula for cos B 2 ac 132 + 152 - 262 Substitute values 2 x 13 x 15 cos y = - 0∙ 723 The negative tells you the angle is obtuse. y = 136. 3 o Use cos-1 -0∙ 723 to find y

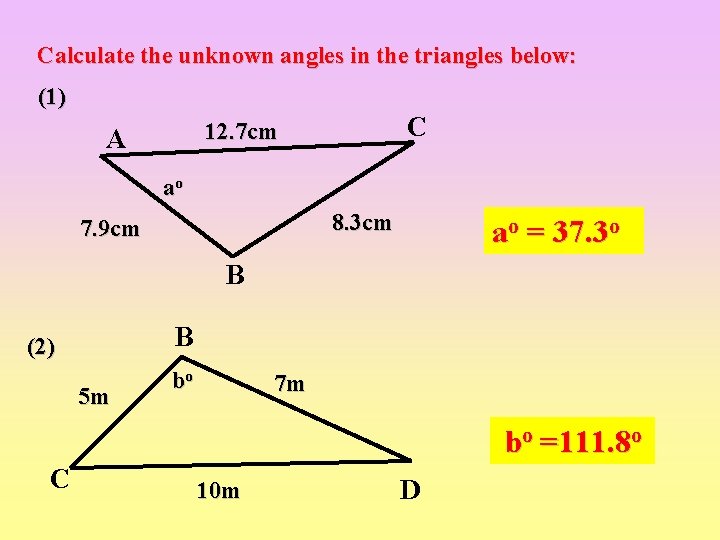
Calculate the unknown angles in the triangles below: (1) C 12. 7 cm A ao 8. 3 cm 7. 9 cm ao = 37. 3 o B B (2) 5 m bo 7 m bo =111. 8 o C 10 m D

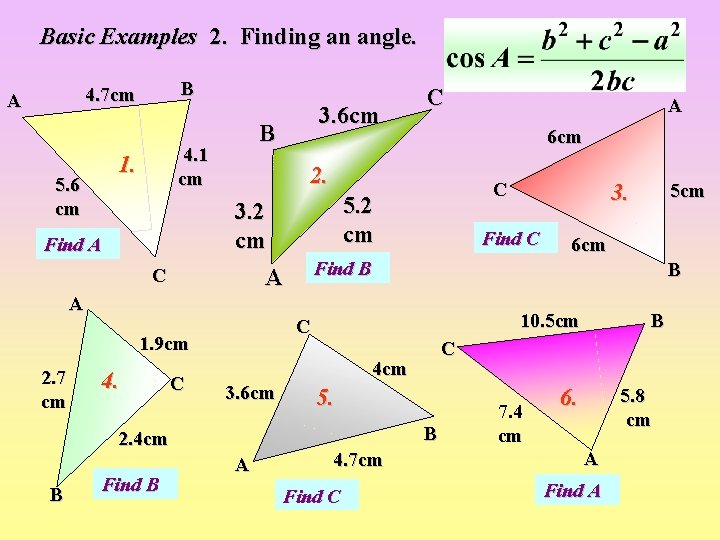
Basic Examples 2. Finding an angle. B 4. 7 cm A 5. 6 cm B 4. 1 cm 1. A C B Find B A 6 cm B 10. 5 cm 5. 4. 7 cm Find C B 2. 4 cm 5 cm Find B 4 cm 3. 6 cm 3. Find C C 1. 9 cm 4. C 5. 2 cm A C A 6 cm 2. 3. 2 cm Find A 2. 7 cm 3. 6 cm C 7. 4 cm 6. 5. 8 cm A Find A

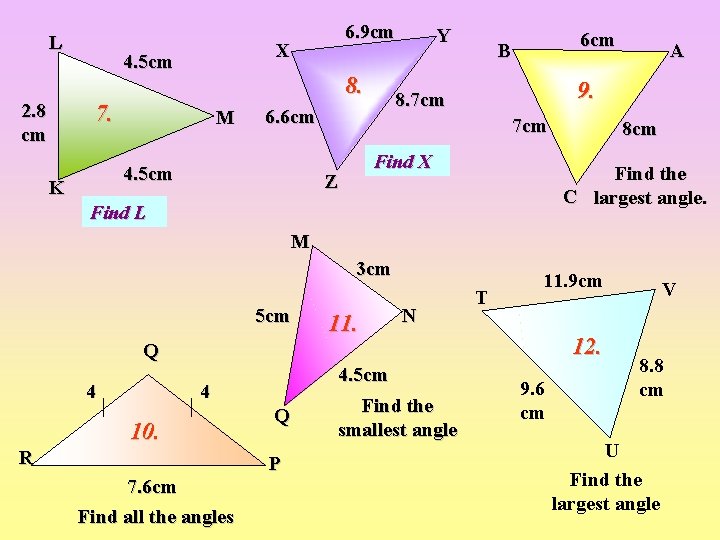
L 2. 8 cm X 4. 5 cm 8. 7. M Y 6 cm B 7 cm Find X Z A 9. 8. 7 cm 6. 6 cm 4. 5 cm K 6. 9 cm 8 cm Find the C largest angle. Find L M 3 cm 5 cm 11. N T 11. 9 cm 12. Q 4 4. 5 cm 4 10. R 7. 6 cm Find all the angles Q P Find the smallest angle 9. 6 cm V 8. 8 cm U Find the largest angle

Cosine Rule or Sine Rule How to determine which rule to use Two questions 1. Do you know the length of ALL the sides? OR SAS 2. Do you know 2 sides and the angle in between? If YES to either of the questions then Cosine Rule Otherwise use the Sine Rule

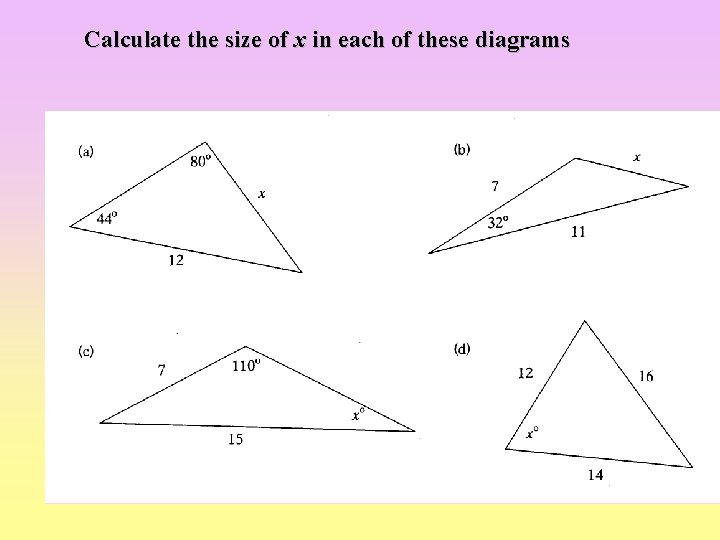
Calculate the size of x in each of these diagrams

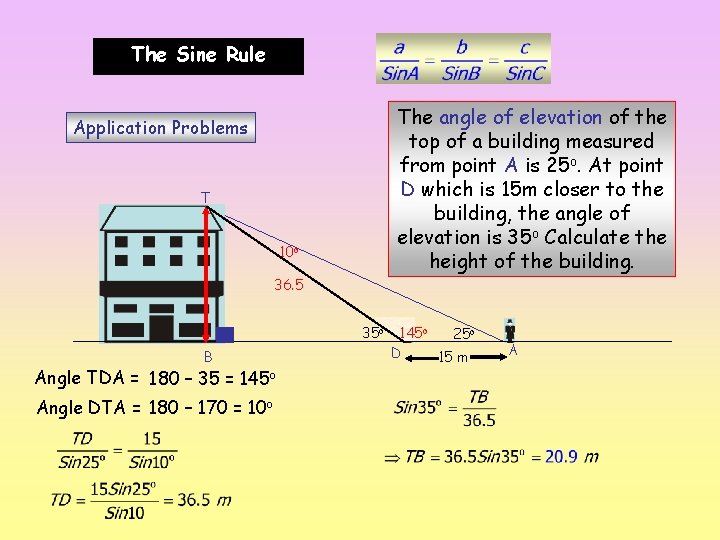
The Sine Rule The angle of elevation of the top of a building measured from point A is 25 o. At point D which is 15 m closer to the building, the angle of elevation is 35 o Calculate the height of the building. Application Problems T 10 o 36. 5 35 o B Angle TDA = 180 – 35 = 145 o Angle DTA = 180 – 170 = 10 o 145 o 25 o D 15 m A

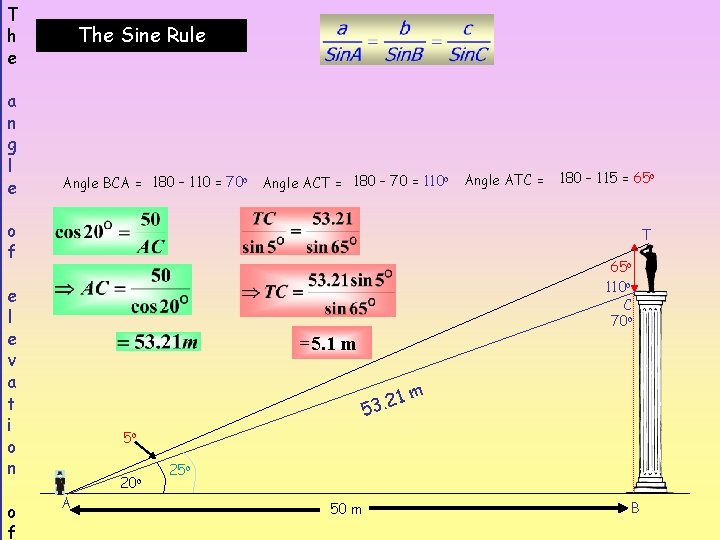
T h e a n g l e The Sine Rule Angle BCA = 180 – 110 = 70 o Angle ACT = 180 – 70 = 110 o o f 180 – 115 = 65 o T 65 o 110 o C 70 o e l e v a t i o n o f Angle ATC = =5. 1 m 21. 3 5 m 5 o A 20 o 25 o 50 m B

The Cosine Rule Application Problems A fishing boat leaves a harbour (H) and travels due East for 40 miles to a marker buoy (B). At B the boat turns left and sails for 24 miles to a lighthouse (L). It then returns to harbour, a distance of 57 miles. (a) Make a sketch of the journey. (b) Find the bearing of the lighthouse from the harbour. (nearest degree) L Bearing = 90 – 20 = 070° N H 57 miles 24 miles 20 A° 40 miles B

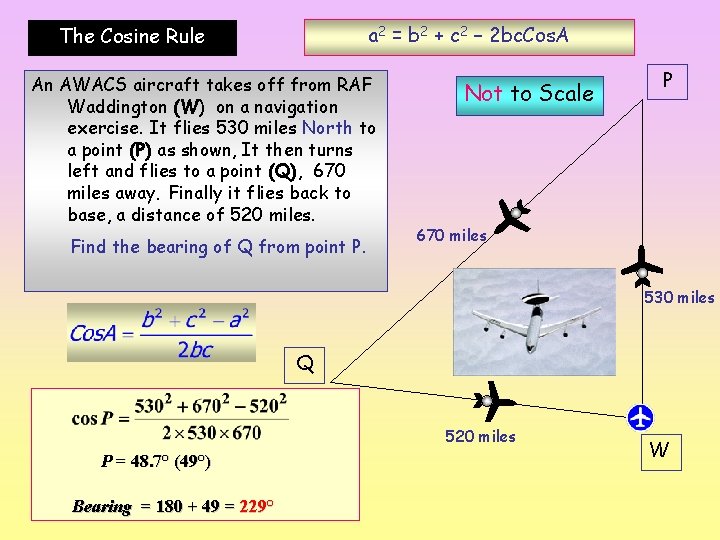
a 2 = b 2 + c 2 – 2 bc. Cos. A The Cosine Rule An AWACS aircraft takes off from RAF Waddington (W) on a navigation exercise. It flies 530 miles North to a point (P) as shown, It then turns left and flies to a point (Q), 670 miles away. Finally it flies back to base, a distance of 520 miles. Find the bearing of Q from point P. Not to Scale P 670 miles 530 miles Q 520 miles P = 48. 7° (49°) Bearing = 180 + 49 = 229° W

COSINE RULE 1. Find the length of the third side of triangle ABC when i) b = 2, c = 5, A = 60° ii) a = 2, b = 5, A = 65° iii) a = 2, c = 5, B = 115° iv) b = 6, c = 8, A = 50° 2. Find QR in ∆PQR in which PR = 4, PQ = 3, P = 18° 3. Find XY in ∆ XYZ in which YZ = 25, XZ = 30, Z = 162° 4. In ∆ ABC, a = 7, b = 4, C = 53°. Calculate c.

5. In ∆ ABC, b = 4· 2, c = 6· 5, A = 24°. Calculate a. 6. In ∆ ABC, a = 1· 64, c = 1· 64, B = 110°. Calculate b. 7. In ∆ ABC, a = 18· 5, b = 22· 6, C = 72· 3°. Calculate c. 8. In ∆ABC, a = 100, b = 120, C = 15°. Calculate c. 9. In ∆ABC, b = 80, c = 100, A = 123°. Calculate a.

10. A town B is 20 km due north of town A and a town C is 15 km north-west of A. Calculate the distance between B and C. 11. Two ships leave port together. One sails on a course of 045° at 9 km/h and the other on a course of 090° at 12 km/h. After 2 h 30 min, how far apart will they be? 12. From a point O, the point P is 3 km distant on a bearing of 040° and the point Q is 5 km distant on a bearing of 123°. What is the distance between P and Q ?

COSINE RULE 1. (1) Solutions Find the length of the third side of triangle ABC when i) a 2 = 22 + 52 2 2 5 cos 60° = 4 + 25 20 0· 5 = 19 a = 4· 36 ii) c 2 = 22 + 52 2 2 5 cos 65° = 4 + 25 20 0· 4226 = 20· 54763 c = 4· 533 iii) b 2 = 22 + 52 2 2 5 cos 115° = 4 + 25 2 2 5 ( 0· 42262 ) = 29 + 8· 45237 = 37· 45237 b = 6· 12 iv) a 2 = 62 + 82 2 6 8 cos 50° = 36 + 64 96 0· 64279 = 100 661· 7076 = 38· 29239 a = 6· 188

2. QR 2 = 42 + 32 2 4 3 cos 18° = 16 + 9 24 0· 951057 = 2· 17464 QR = 1· 4747 3. XY 2 = 252 + 302 2 25 30 cos 162° = 625 + 900 1500 ( 0· 951057 ) = 1525 + 1426· 5848 = 2951· 5848 XY = 54· 33 4. c 2 = 72 + 42 2 7 4 cos 53° = 31· 2984 c = 5· 5945

5. a 2 = 4· 22 + 6· 52 2 4· 2 6· 5 cos 24° = 17· 64 + 42· 25 554· 6 0· 91355 = 10· 0104 6. a = 3· 164 b 2 = 1· 642 + 1· 642 2 1· 64 cos 110° = 2 2· 6896 ( 0· 34202 ) = 7· 2190 7. c 2 = 18· 52 + 22· 62 2 18· 5 22· 6 cos 72· 3° = 598· 778 8. b = 2· 6868 c = 24· 50 c 2 = 1002 + 1202 2 100 120 cos 15° = 1217· 780 c = 34· 90

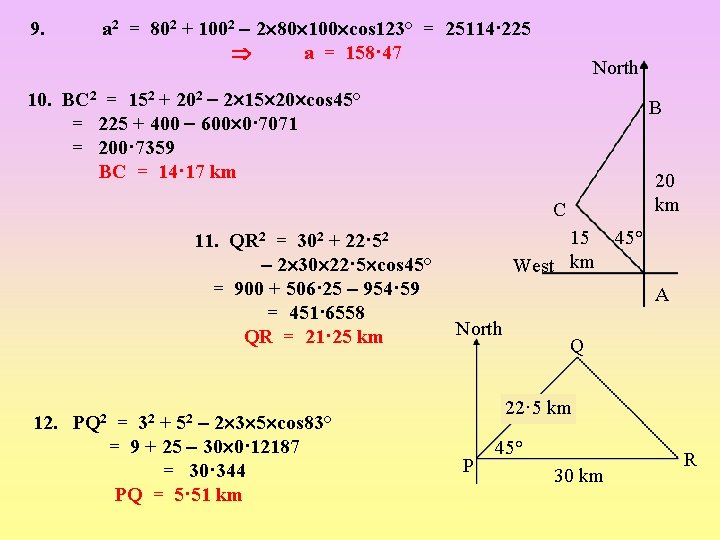
9. a 2 = 802 + 1002 2 80 100 cos 123° = 25114· 225 a = 158· 47 North 10. BC 2 = 152 + 202 2 15 20 cos 45° = 225 + 400 600 0· 7071 = 200· 7359 BC = 14· 17 km B 20 km C 11. QR 2 = 302 + 22· 52 2 30 22· 5 cos 45° = 900 + 506· 25 954· 59 = 451· 6558 QR = 21· 25 km 12. PQ 2 = + 2 3 5 cos 83° = 9 + 25 30 0· 12187 = 30· 344 PQ = 5· 51 km 32 15 45° West km A North Q 22· 5 km 52 P 45° 30 km R

Cosine Rule Bearings problems

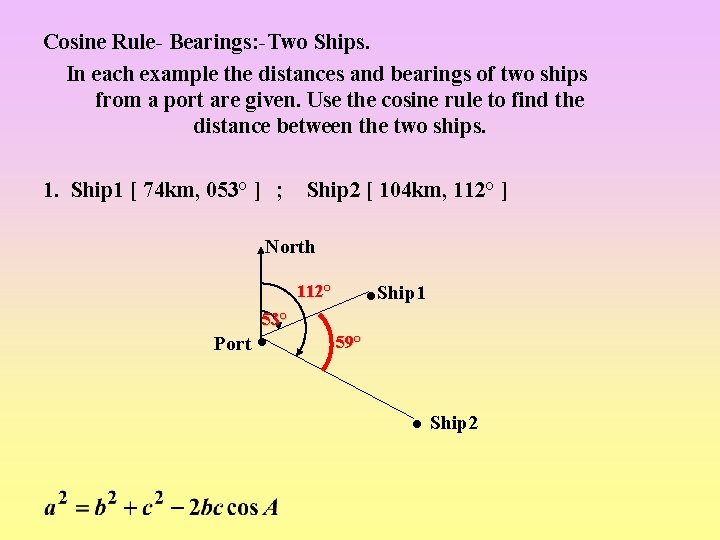
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 1. Ship 1 [ 74 km, 053° ] ; Ship 2 [ 104 km, 112° ] North 112° 53° Port Ship 1 59° Ship 2

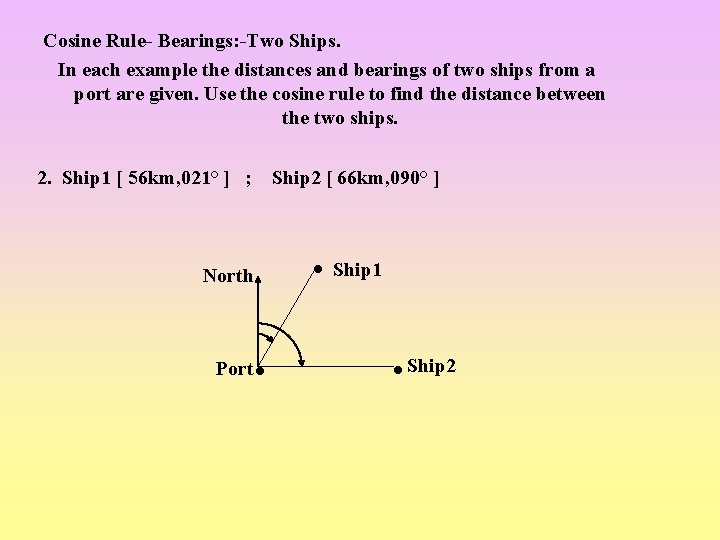
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 2. Ship 1 [ 56 km, 021° ] ; North Port Ship 2 [ 66 km, 090° ] Ship 1 Ship 2

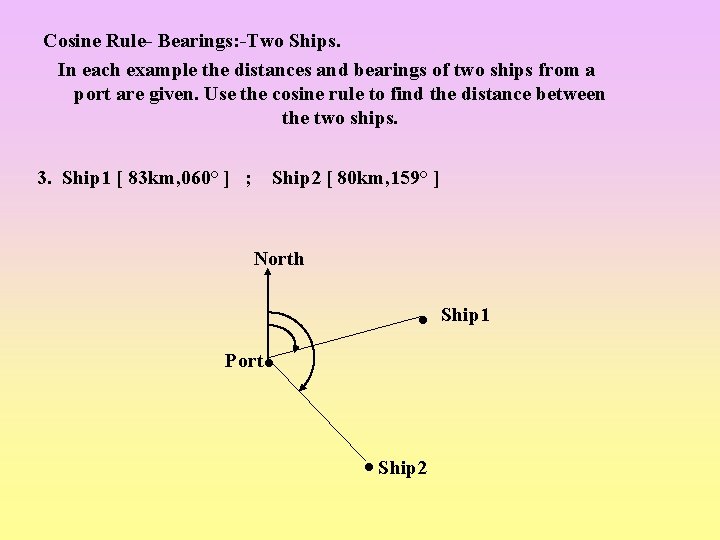
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 3. Ship 1 [ 83 km, 060° ] ; Ship 2 [ 80 km, 159° ] North Ship 1 Port Ship 2

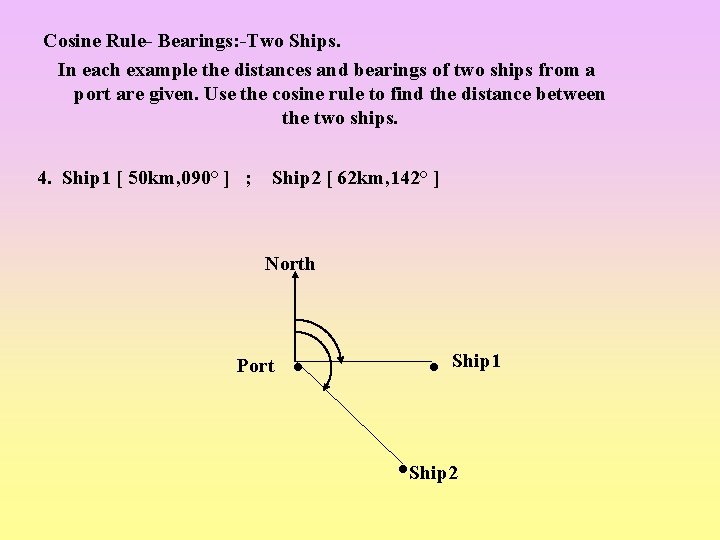
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 4. Ship 1 [ 50 km, 090° ] ; Ship 2 [ 62 km, 142° ] North Port Ship 1 Ship 2

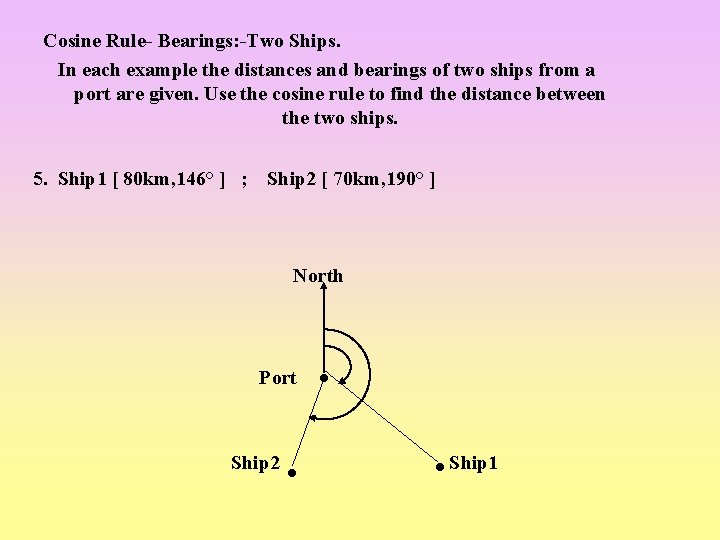
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 5. Ship 1 [ 80 km, 146° ] ; Ship 2 [ 70 km, 190° ] North Port Ship 2 Ship 1

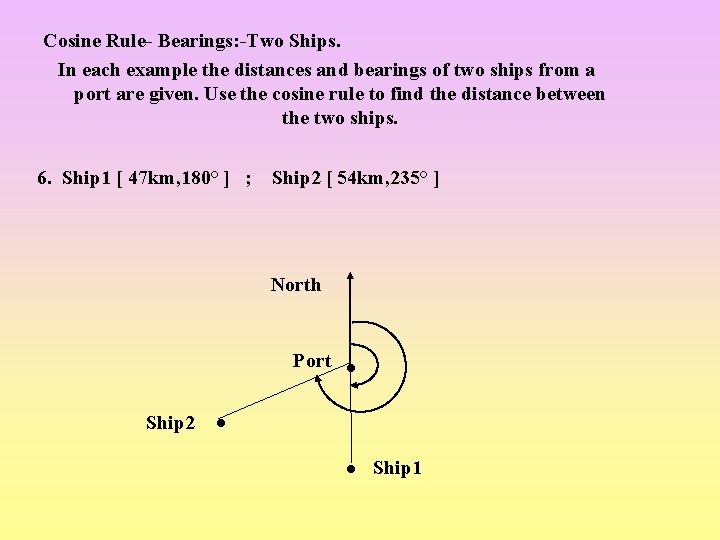
Cosine Rule- Bearings: -Two Ships. In each example the distances and bearings of two ships from a port are given. Use the cosine rule to find the distance between the two ships. 6. Ship 1 [ 47 km, 180° ] ; Ship 2 [ 54 km, 235° ] North Port Ship 2 Ship 1

Bearings Problems 1. Dundee is 84 km due south of Aberdeen. 2. A ship at sea is on a bearing of 078° from Aberdeen and 048° from Dundee. How far is the ship from Dundee and from Aberdeen ? 2. An aeroplane is 240 km from an airport on a bearing of 100° while a helicopter is 3. 165 km from the airport on a bearing of 212°. How far apart are the aircraft ?

Bearings Problems 3. A ship sails 80 km on a bearing of 060° from its home port. 4. It then sails 93 km on a bearing of 134°. 5. How far is it now from its home port ? 4. Glasgow airport is 73 km from Edinburgh airport and lies 5. to the west of Edinburgh airport. 6. The bearing of an aeroplane from Glasgow airport is 040° while 7. its bearing from Edinburgh airport is 300°. 8. How far is the aeroplane from each airport ?

Bearings Problems 5. A ship sails 74 km south from its port to a lighthouse. 6. It then sails 85 km on a bearing of 160°. 7. How far is the ship from the port ? 6. From a port P, ship A is 144 km distant on a bearing of 036° and 7. ship B is 97 km distant on a bearing of 114°. 8. What is the distance between the two ships ?

Bearings Problems 7. A ship sails 93 km on a bearing 054° and then 8. another 108 km on a bearing of 110°. 9. How far is it now from its starting point ? 8. Two radar stations Alpha and Beta pick up signals from an incoming aircraft. Alpha is 40 km east of Beta and picks up the signals on a bearing of 300°. Beta picks up the signals on a bearing of 070°. How far is the aircraft from Alpha and from Beta ?

Bearings Problems 9. Aeroplane P is 200 km from an airport on a bearing of 208° while aeroplane Q is 170 km from the same airport on a bearing of 094°. How far apart are the two aeroplanes ? 10. The bearings and distances from Aberdeen of three oil platforms are : a) 028° 116 km b) 081° 104 km c) 138° 97 km A supply boat leaves Aberdeen, visits each platform and then returns to Aberdeen. Find the total length of the journey.