TRIGONOMETRI Pertemuan 1 Perbandingan Trigonometri dalam sikusiku g

TRIGONOMETRI Pertemuan 1

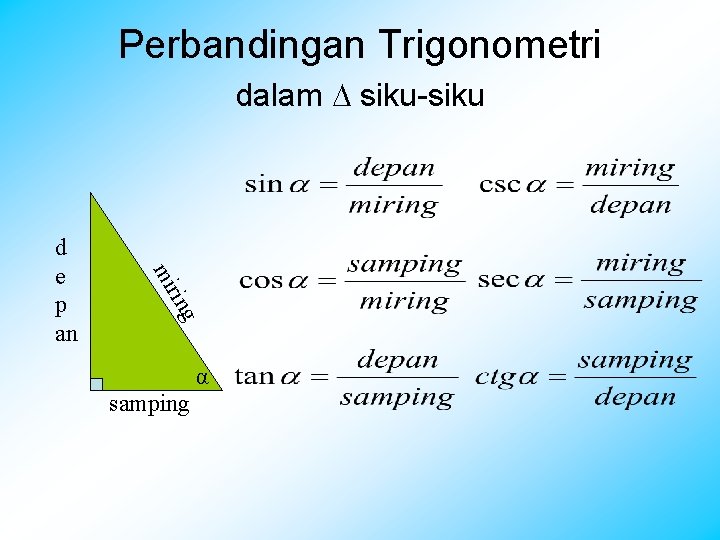
Perbandingan Trigonometri dalam siku-siku g rin mi d e p an α samping

Latihan 1 r sin α = sin β = cos α = cos β = tan α = tan β = p α q β

Segitiga Siku-Siku Istimewa 300 sin 30 o= 1/2 cos 30 o= √ 3/2 sin 60 o= √ 3/2 cos 60 o= 1/2 tan 30 o= 1/√ 3 tan 60 o= √ 3 sin 45 o= 1/√ 2 cos 45 o= tan 45 o= 1 2 450 1 600 1 450 1 Bagaimana jika segitiganya tidak istimewa?

Latihan 2 Tentukan nilai a! √ 160 15 3 a 7 a a 25 o a 45 50 o ao 30 10 Jawab: 2 70 32, 17 19, 47

Contoh Soal no 3 • Tentukan x, k, dan h ! 7 x 320 5 Ans : 4, 37 25, 40 x Ans : 10, 53 k h 53, 320 10 Ans : h = 13, 43 k = 16. 74

Sudut Elevasi dan Depresi Sudut depresi mobil Sudut elevasi layang-layang

LATIHAN Kerjakan latihan dari kertas fotocopy yang dibagikan hal. 2 no. 2 sampai dengan 8

TRIGONOMETRY Pertemuan 2

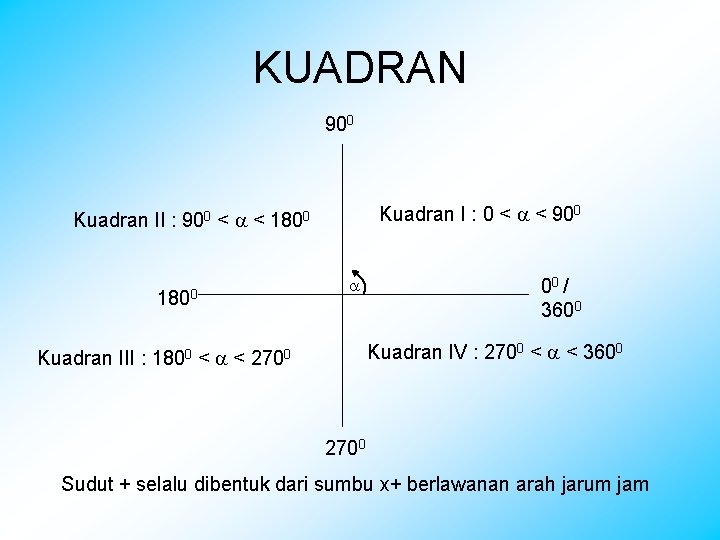
KUADRAN 900 Kuadran I : 0 < < 900 Kuadran II : 900 < < 1800 00 / 3600 Kuadran IV : 2700 < < 3600 Kuadran III : 1800 < < 2700 Sudut + selalu dibentuk dari sumbu x+ berlawanan arah jarum jam

Perbandingan Trigonometri dalam koordinat Cartesius sin α = (x, y) y r x cos α = x tan α = r = x 2+y 2 (selalu +) y Note : Sudut selalu dimulai dari sb x positif berlawanan arah jarum jam

Bagaimana untuk sudut istimewa 0 o dan 90 o P(0, y) r= 90 o y sin 90 o = =1 cos 90 o = tan 90 o = 0 =0 sin 0 o = cos 0 o = =~ tan 0 o = 0 P(x, 0) 0 o r= x 1

Perbandingan Trigonometri dalam koordinat Cartesius r= (-2, 3) 3 r -2

P(x, y) sin 2=y/r (+) cos 2=x/r (-) tan 2=y/x (-) r y 2 di kuadran II P(x, y) r 2 x x sin 1=y/r (+) cos 1=x/r (+) y tan 1=y/x (+) 1 x 1 di kuadran I 3 x 4 y r 3 di kuadran III sin 3=y/r (-) cos 3=x/r (-) tan 3=y/x (+) r sin 4=y/r (-) cos 4=x/r (+) y tan =y/x (-) 4 P(x, y) 4 di kuadran IV

Tanda Perbandingan Trigonometri 90 o sin, csc + 180 o Semua + 0 o II I III IV tan, ctg + 360 o cos, sec + 270 o

Contoh Soal 1. Diketahui tan =-5/12, sudut di kuadran IV, hitunglah : cot cos csc -12/5 12/13 -13/5 2. Diketahui cos =1/3, hitunglah: KW IV: a. sin 2 2/3 -2 2/3 b. tan 2 2 -2 2

Sudut-sudut Berelasi 90 o sin (90 o+ )=cos sin (90 o- )=cos cos(90 o+ )=-sin cos(90 o- )=sin tan(90 o+ )=-cot sin (180 o- )=sin tan(90 o- )=cot sin (360 o+ )=sin cos(180 o- )=-cos cos(360 o+ )=cos tan(180 o- )=-tan II I sin (180 o+ )=-sin III IV 180 o tan(360 o+ )=tan sin (360 o- )=sin(- )=-sin cos(180 o+ )=-cos cos(360 o- )=cos(- )=cos tan(180 o+ )=tan tan(360 o- )=tan(- )=-tan sin (270 o- )=-cos sin (270 o+ )=-cos cos(270 o- )=-sin cos(270 o+ )=sin tan(270 o- )=cot 270 o tan(270 o+ )=-cot 0 o 360 o

Trigonometri Pertemuan III-Identitas

Idetitas trigonometri Berdasarkan geometri analitis: sin =y/r y=r. sin cos =x/r x=r. cos r 2=x 2+y 2, maka: r 2= (r. sin )2+(r. cos )2 r 2= r 2(sin 2 + cos 2 ) Sehingga : sin 2 + cos 2 =1

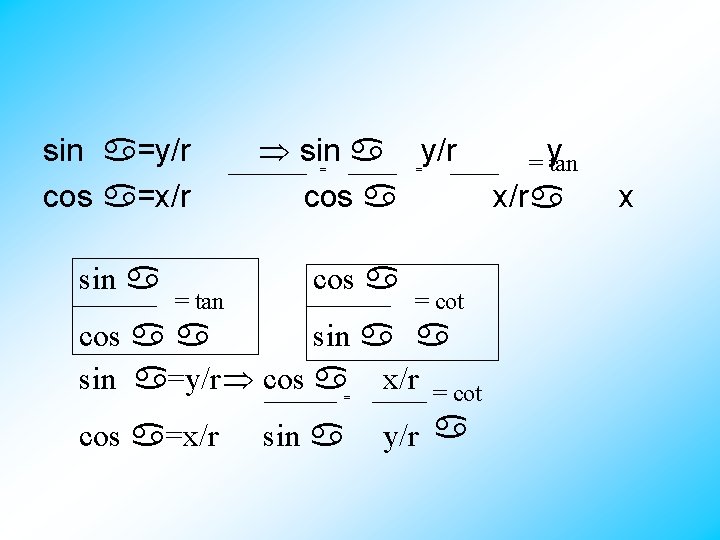
sin =y/r cos =x/r sin =y/r = cos sin cos = tan = cot cos sin =y/r cos = x/r = cot cos =x/r sin y/r =y tan x/r x

sin 2 + cos 2 =1 Bagi kedua ruas dengan sin 2 : 1+cot 2 =csc 2 sin 2 + cos 2 =1 Bagi kedua ruas dengan cos 2 : tan 2 +1=sec 2

Contoh Penggunaan Rumus Identitas • Diketahui sin A=5/13 dan 90 o<A<180 o Tetukan nilai cos A & tan A! Jwb sin 2 A + cos 2 A =1 - sin 2 A cos A= 1 - sin 2 A, karena 90 o<A<180 o, maka cos A<0 cos A=- 1 - sin 2 A cos A=- 1 -(5/13) 2= 144/169=-12/13 tan. A=sin. A/cos. A=5/13: -12/13==-5/12

Rangkuman Identitas dasar: 1. sin 2 + cos 2 =1 2. : cos sin = tan cos = cot sin 3. 1+cot 2 =csc 2 4. tan 2 +1=sec 2

Cara Mudah menghafal sudut Istimewa • Grafik sinus

• Grafik cos

• Grafik sin dan cos

• Grafik Tan