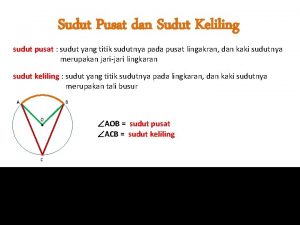
TRIGONOMETRI PERBANDINGAN TRIGONOMETRI SUATU SUDUT C sin A

TRIGONOMETRI

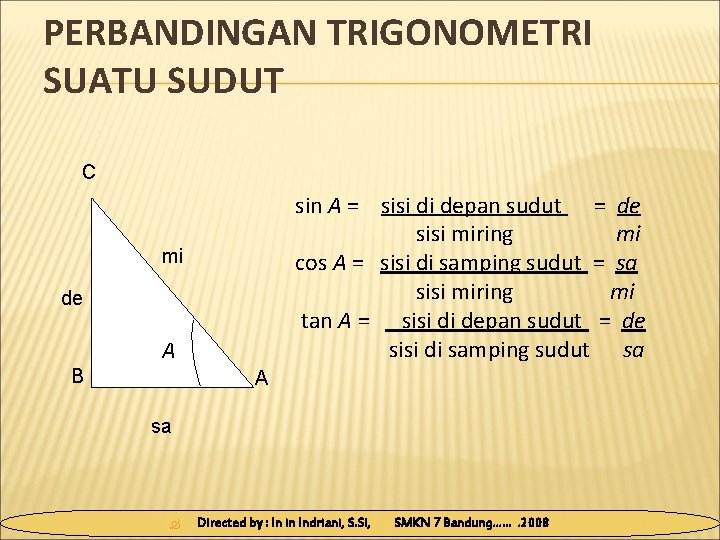
PERBANDINGAN TRIGONOMETRI SUATU SUDUT C sin A = sisi di depan sudut = de sisi miring mi cos A = sisi di samping sudut = sa sisi miring mi tan A = sisi di depan sudut = de sisi di samping sudut sa mi de A B A sa Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

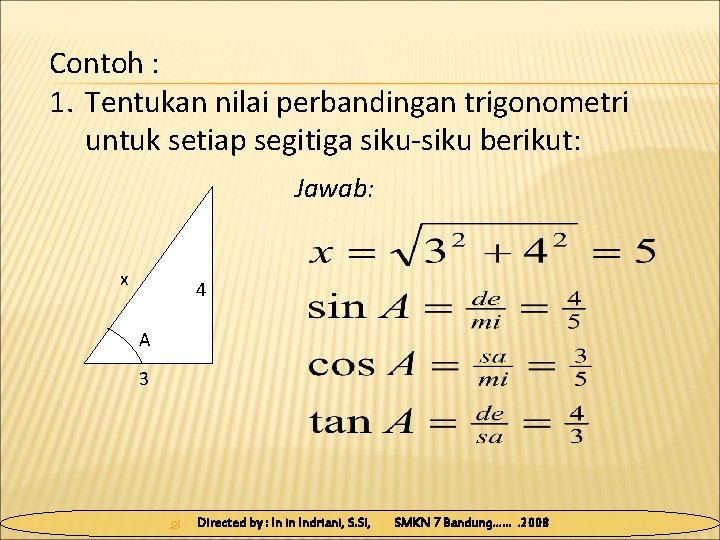
Contoh : 1. Tentukan nilai perbandingan trigonometri untuk setiap segitiga siku-siku berikut: Jawab: x 4 A 3 Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

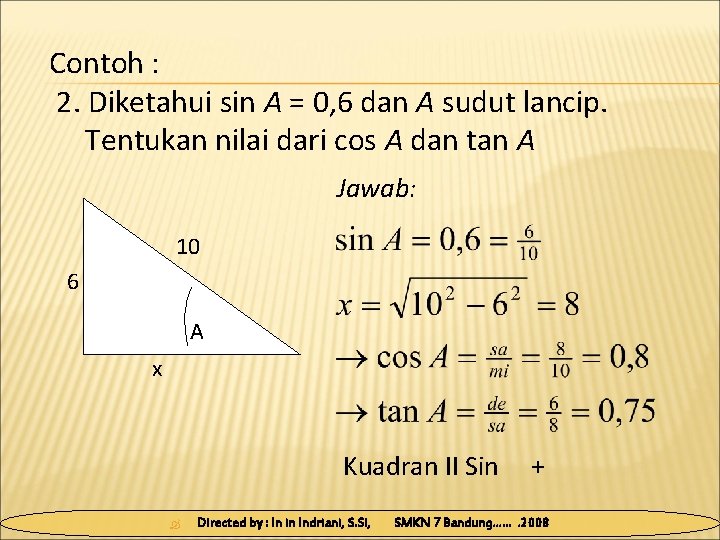
Contoh : 2. Diketahui sin A = 0, 6 dan A sudut lancip. Tentukan nilai dari cos A dan tan A Jawab: 10 6 A x Kuadran II Sin Directed by : In in Indriani, S. Si, + SMKN 7 Bandung……. 2008

SUDUT-SUDUT ISTIMEWA A 0 o 30 o 45 o 60 o 90 o 180 o 270 o 360 o Sin A 0 1 0 -1 0 Cos A 1 0 -1 0 1 � 0 Tan A 0 1 Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

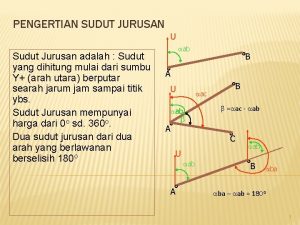
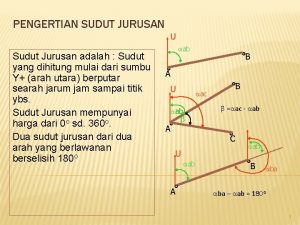
PERBANDINGAN TRIGONOMETRI DI BERBAGAI KUADRAN Kuadran II Kuadran I sin Semua + + Kuadran III Kuadran IV tan cos + + Kuadran I sin (90 -A)o = cos A cos (90 -A)o = sin A tan (90 -A)o = cot A Kuadran II sin (180 -A)o = sin A cos (180 -A)o = -cos A tan (180 -A)o = -tan A Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

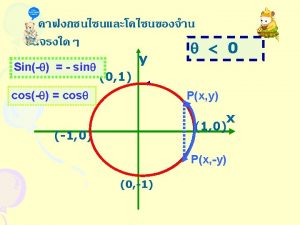
Kuadran III sin (180+A)o = -sin A cos (180+A)o = -cos A tan (180+A)o = tan A Sudut Negatif sin (-A)o = -sin A cos (-A)o = cos A tan (-A)o = -tan A Kuadran IV sin (360 -A)o = -sin A cos (360 -A)o = cos A tan (360 -A)o = -tan A Perioditas Trigonometri sin (n. 360+A)o = sin A cos (n. 360+A)o = cos A tan (n. 180+A)o = tan A Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 1. Tentukan nilai dari sin 150 o Jawab: sin 150 o = sin (180 -30)o = sin 30 o = 2. Tentukan nilai dari cos 1950 o Jawab: cos 1950 o = cos (5 x 360+150)o = cos 150 o = cos (180 -30)o = -cos 30 o = Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

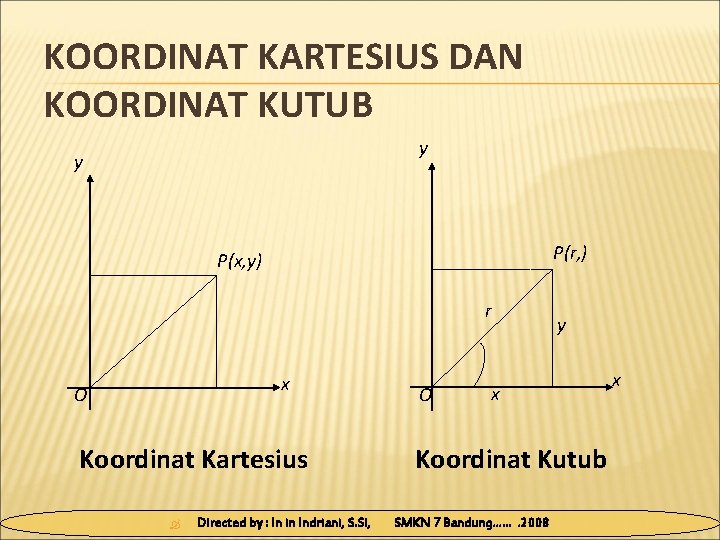
KOORDINAT KARTESIUS DAN KOORDINAT KUTUB y y P(r, ) P(x, y) r x O Koordinat Kartesius Directed by : In in Indriani, S. Si, O y x Koordinat Kutub SMKN 7 Bandung……. 2008 x

KONVERSI KOORDINAT KARTESIUS KE KOORDINAT KUTUB DAN SEBALIKNYA

Contoh: 1. Tentukan koordinat kutub jika koordinat kartesius dari P y Jawab: O x r Karena P berada di kuadran III Maka Jadi koordinat kutubnya Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 2. Tentukan koordinat kartesius jika koordinat kutub P(6, 120 o) Jawab: Jadi koordinat karetesiusnya Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

IDENTITAS TRIGONOMETRI Buktikan bahwa : Bukti: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

IDENTITAS TRIGONOMETRI Buktikan bahwa : Bukti: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

ATURAN SINUS DAN COSINUS C Aturan Sinus b Aturan Cosinus Directed by : In in Indriani, S. Si, A a c SMKN 7 Bandung……. 2008 B

Contoh: 1. Diketahui segitiga ABC dengan besar A = 30 o, B=45 o, dan sisi b = 10 cm. Tentukan a. besar C b. panjang a c. panjang c Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 2. Hitunglah panjang ketiga sisi jika diketahui a = 6 cm, c = 4 cm, Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

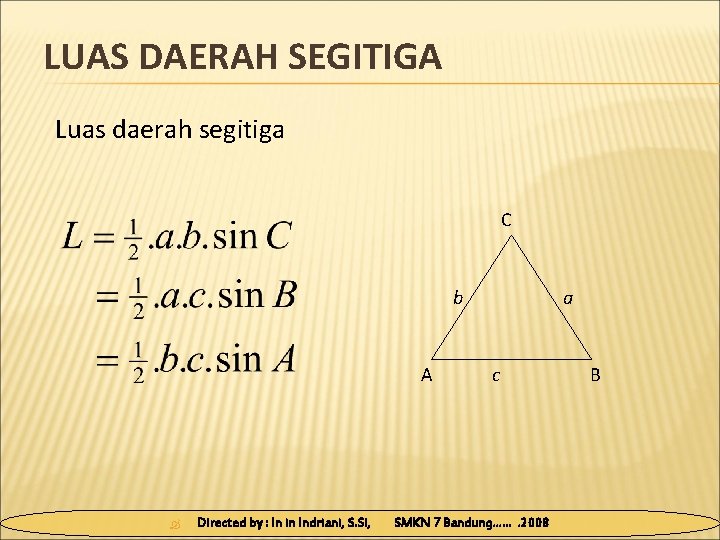
LUAS DAERAH SEGITIGA Luas daerah segitiga C b A Directed by : In in Indriani, S. Si, a c SMKN 7 Bandung……. 2008 B

Contoh: Hitunglah luas daerah segitiga ABC sama sisi dengan panjang sisi 20 cm Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

RUMUS TRIGONOMETRI JUMLAH DAN SELISIH DUA SUDUT Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 1. Dengan menggunakan sudut-sudut istimewa tentukan nilai dari sin 15 o Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 2. Jika sin 5 o = p dan cos 5 o = q dalam p dan q: sin 35 o Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

PERSAMAAN TRIGONOMETRI a. sin x = A b. cos x = A c. Diubah ke dalam bentuk dengan Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 1. Tentukan himpunan penyelesaian dari persamaan berikut, untuk a. b. Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Contoh: 2. Tentukan himpunan penyelesaian dari , untuk Jawab: Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008

Directed by : In in Indriani, S. Si, SMKN 7 Bandung……. 2008