PreCalculus 4 3 Right Triangle Trigonometry 1 The

Pre-Calculus 4 -3 Right Triangle Trigonometry 1

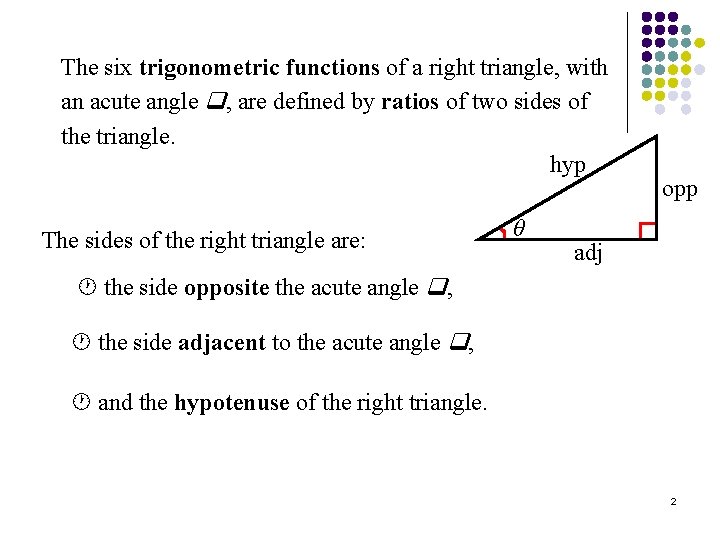
The six trigonometric functions of a right triangle, with an acute angle , are defined by ratios of two sides of the triangle. hyp The sides of the right triangle are: θ opp adj the side opposite the acute angle , the side adjacent to the acute angle , and the hypotenuse of the right triangle. 2

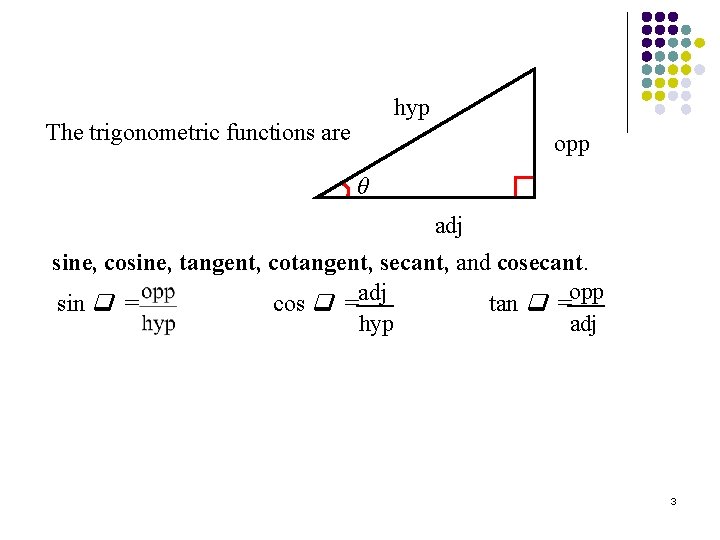
hyp The trigonometric functions are opp θ adj sine, cosine, tangent, cotangent, secant, and cosecant. sin = cos =adj tan =opp hyp adj 3

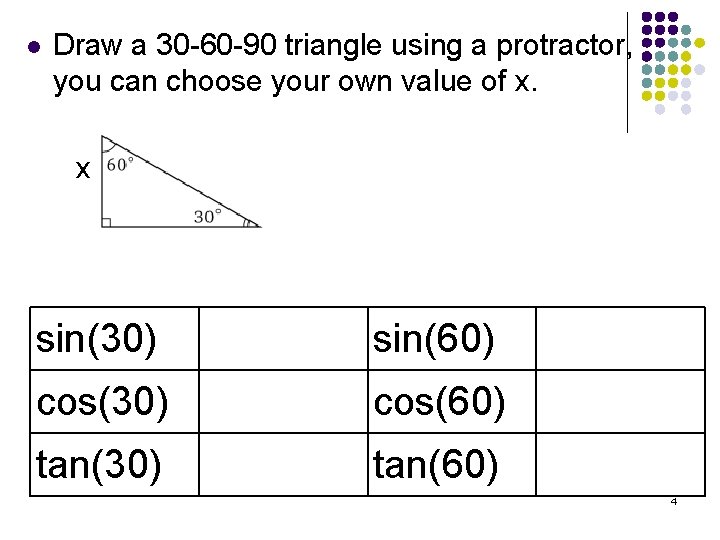
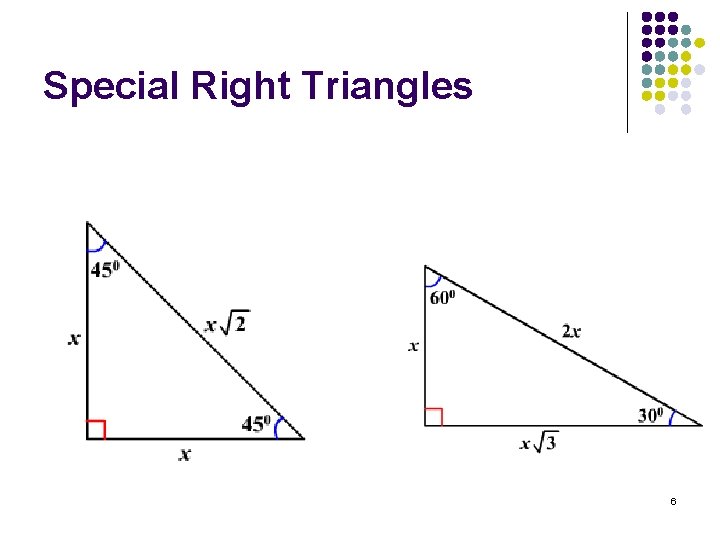
l Draw a 30 -60 -90 triangle using a protractor, you can choose your own value of x. x sin(30) sin(60) cos(30) cos(60) tan(30) tan(60) 4

l Draw a 45 -45 -90 triangle using a protractor (or properties of isosceles triangles), you can choose your own value of x. x sin(45) cos(45) tan(45) Repeat for at least one additional value of x for each triangle. Then determine the relationships between the sides using the x as a variable to represent any length. 5

Special Right Triangles 6

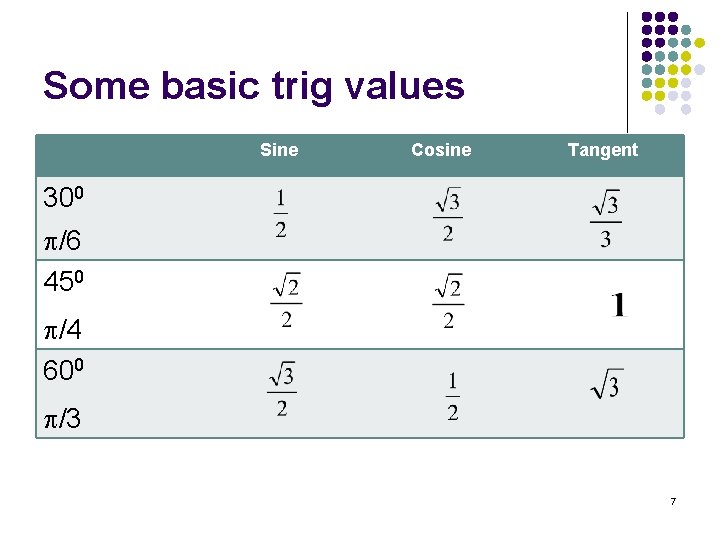
Some basic trig values Sine Cosine Tangent 300 /6 450 /4 600 /3 7

hyp The trigonometric functions are opp θ adj sine, cosine, tangent, cotangent, secant, and cosecant. sin = cos =adj tan =opp hyp adj hyp csc = opp sec =hyp adj cot =adj opp Note: sine and cosecant are reciprocals, cosine and secant are reciprocals, and tangent and cotangent are reciprocals. 8

Reciprocal Functions Another way to look at it… sin = 1/csc cos = 1/sec tan = 1/cot csc = 1/sin sec = 1/cos cot = 1/tan 9

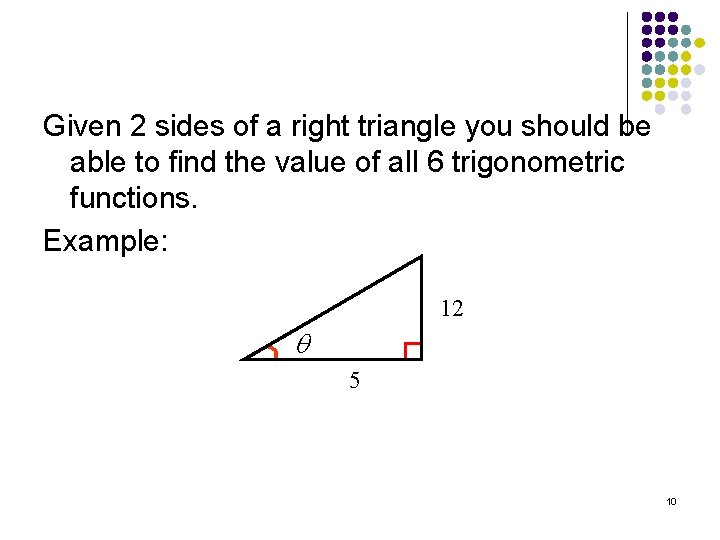
Given 2 sides of a right triangle you should be able to find the value of all 6 trigonometric functions. Example: 12 5 10

Calculate the trigonometric functions for . Calculate the trigonometric functions for . 5 The six trig ratios are sin = cos = tan = cot = sin α = cos α = tan α = cot α = sec α = csc α = 4 3 What is the relationship of α and θ? They are complementary (α = 90 – θ) 11

Cofunctions sin = cos (90 ) cos = sin (90 ) sin = cos (π/2 ) cos = sin (π/2 ) tan = cot (90 ) cot = tan (90 ) tan = cot (π/2 ) cot = tan (π/2 ) sec = csc (90 ) csc = sec (90 ) sec = csc (π/2 ) csc = sec (π/2 ) 12

Trigonometric Identities are trigonometric equations that hold for all values of the variables. We will learn many Trigonometric Identities and use them to simplify and solve problems. 13

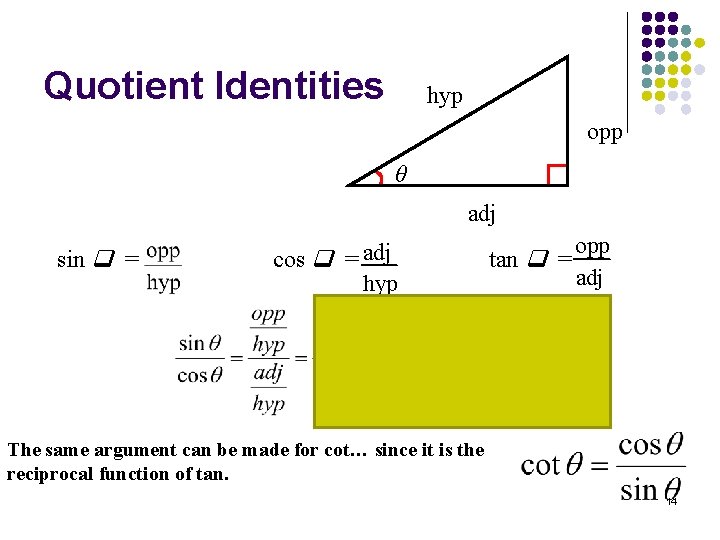
Quotient Identities hyp opp θ adj sin = cos = adj hyp tan = opp adj The same argument can be made for cot… since it is the reciprocal function of tan. 14

Quotient Identities Important Question: Why do mathematicians never go the beach? 15

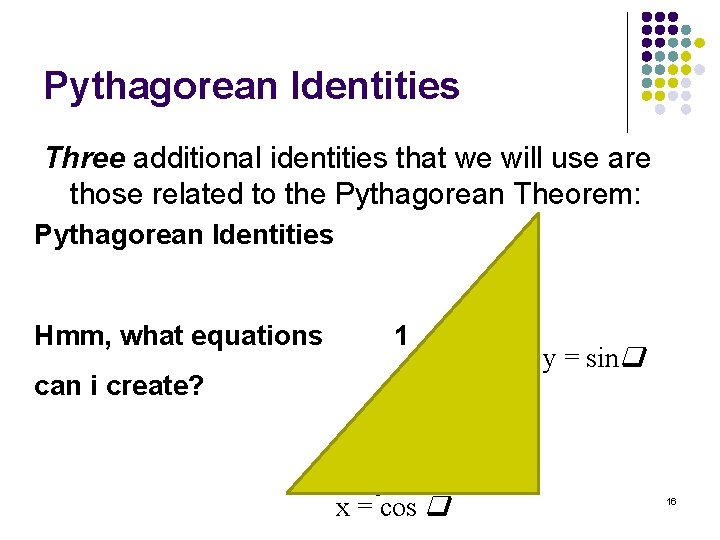
Pythagorean Identities Three additional identities that we will use are those related to the Pythagorean Theorem: Pythagorean Identities Hmm, what equations 1 can i create? 1 x = cos y = sin 16

Pythagorean Identities Three additional identities that we will use are those related to the Pythagorean Theorem: Pythagorean Identities sin 2 + cos 2 = 1 tan 2 + 1 = sec 2 cot 2 + 1 = csc 2 17

IDENTITIES WE HAVE REVIEWED SO FAR… 18

Fundamental Trigonometric Identities Reciprocal Identities sin = 1/csc cot = 1/tan cos = 1/sec = 1/cos tan = 1/cot csc = 1/sin Co function Identities sin = cos(90 ) sin = cos (π/2 ) tan = cot(90 ) tan = cot (π/2 ) sec = csc(90 ) sec = csc (π/2 ) Quotient Identities tan = sin /cos = sin(90 ) cos = sin (π/2 ) cot = tan(90 ) cot = tan (π/2 ) csc = sec(90 ) csc = sec (π/2 ) cot = cos /sin Pythagorean Identities sin 2 + cos 2 = 1 tan 2 + 1 = sec 2 cot 2 + 1 = csc 2 19

Example: Given sec = 4, find the values of the other five trigonometric functions of . Draw a right triangle with an angle such that 4 = sec = hyp = adj 4 . Use the Pythagorean Theorem to solve for the third side of the triangle. θ 1 sin = csc = = cos = sec = =4 tan = = cot = 20

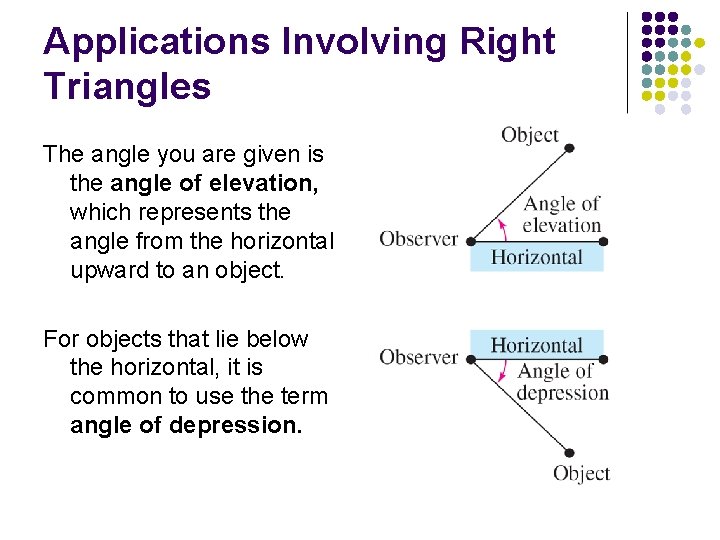
Applications Involving Right Triangles The angle you are given is the angle of elevation, which represents the angle from the horizontal upward to an object. For objects that lie below the horizontal, it is common to use the term angle of depression.

Using Trigonometry to Solve a Right Triangle A surveyor is standing 115 feet from the base of the Washington Monument. The surveyor measures the angle of elevation to the top of the monument as 78. 3. How tall is the Washington Monument? Figure 4. 33

Solution where x = 115 and y is the height of the monument. So, the height of the Washington Monument is y = x tan 78. 3 115(4. 82882) 555 feet.

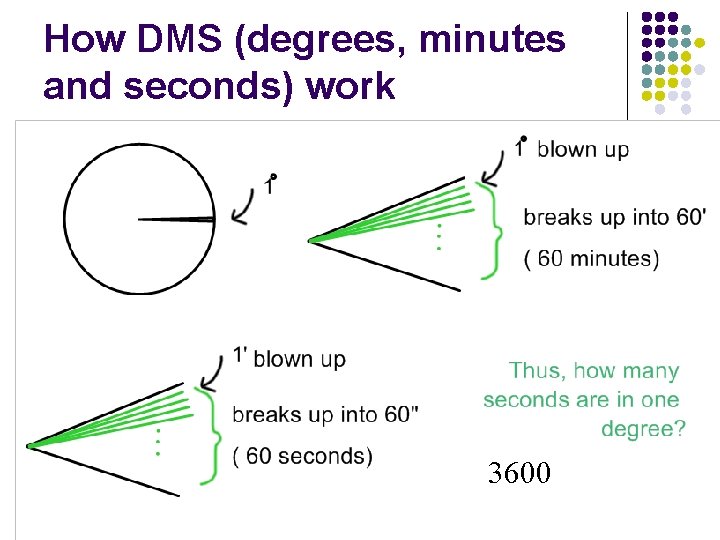
How DMS (degrees, minutes and seconds) work 3600 24

Convert 27 15' 32. 4" to decimal degrees 25

Or you can use a calculator Convert 27 15' 32. 4" to decimal degrees l l Hit 2 nd apps (angle) to find your homepage for DMS Use Alpha/Plus (Quote) for the seconds symbol Convert 27. 259 to DMS 26

H Dub l 4 -3 Page 308 #9 -25 odd, 29 -42 all, 43 -57 odd, 63, 66 -68 27

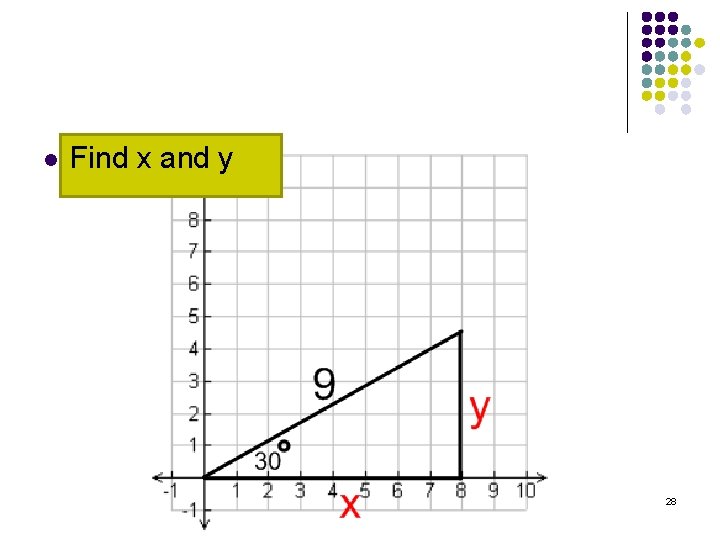
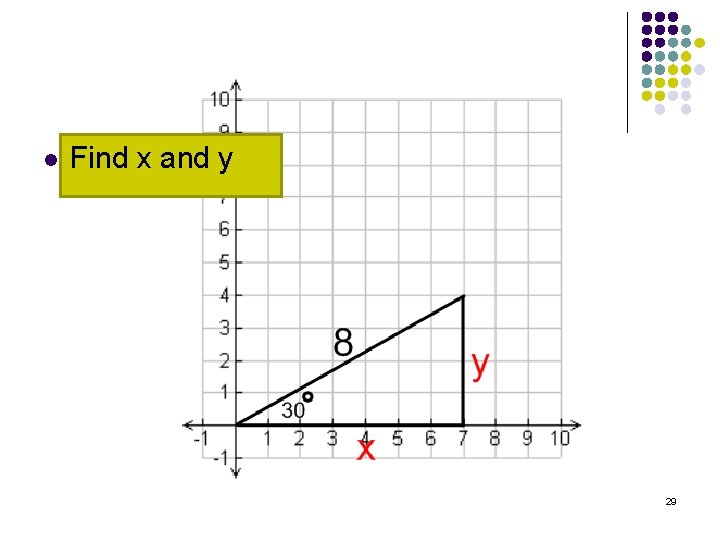
l Find x and y 28

l Find x and y 29

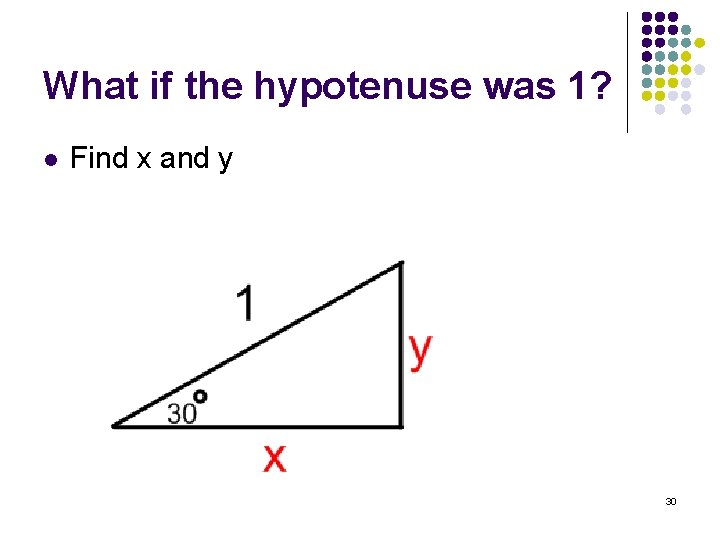
What if the hypotenuse was 1? l Find x and y 30

Stuff we went over in 4. 2 31

Some old geometry favorites… Let’s look at the trigonometric functions of a few familiar triangles… 32

Geometry of the 45 -45 -90 triangle Consider an isosceles right triangle with two sides of length 1. 45 1 The Pythagorean Theorem implies that the hypotenuse is of length. 33

Calculate the trigonometric functions for a 45 angle. 1 45 1 = adj cos 45 = = hyp = opp tan 45 = = adj = 1 adj cot 45 = = opp = 1 hyp sec 45 = = adj = hyp csc 45 = = opp = sin 45 = = 34

Geometry of the 30 -60 -90 triangle Consider an equilateral triangle with each side of length 2. 30○ The three sides are equal, so the angles are equal; each is 60. 2 The perpendicular bisector of the base bisects the opposite angle. 60○ 2 1 Use the Pythagorean Theorem to find the length of the altitude, . 35

Calculate the trigonometric functions for a 30 angle. 2 1 30 sin 30 = adj cos 30 = = hyp = opp tan 30 = = adj hyp sec 30 = = adj = opp = cot 30 = = hyp csc 30 = = opp = = 2 36

Note sin = cos(90 ), for 0 < < 90 Note that and 90 are complementary angles. hyp Side a is opposite θ and also adjacent to 90○– θ a θ b sin = and cos (90 ) = . So, sin = cos (90 ). Note : These functions of the complements are called cofunctions. 37

Calculate the trigonometric functions for a 60 angle. 2 60○ 1 sin 60 = tan 60 = = opp = adj hyp sec 60 = = adj cos 60 = = hyp = cot 60 = adj = opp = = 2 hyp csc 60 = = opp = 38