NEXT MENU PERBANDINGAN TRIGONOMETRI SUDUT SUDUT PADA SEMUA

NEXT

MENU :

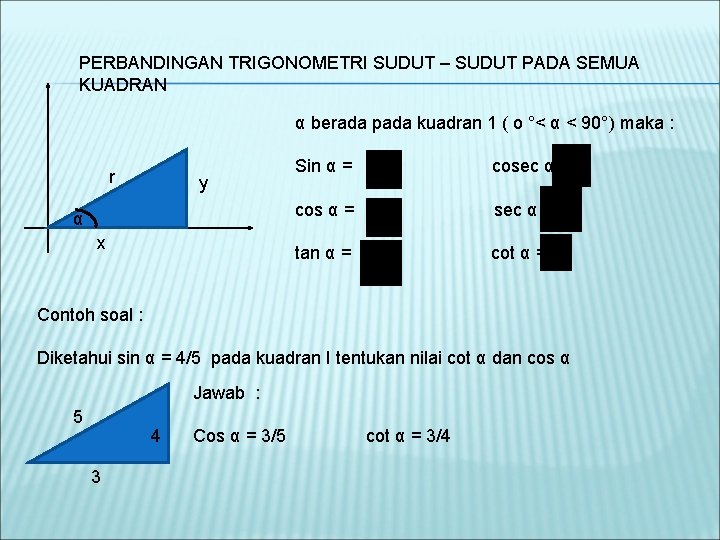
PERBANDINGAN TRIGONOMETRI SUDUT – SUDUT PADA SEMUA KUADRAN α berada pada kuadran 1 ( o °< α < 90°) maka : r y α x Sin α = cosec α = cos α = sec α = tan α = cot α = Contoh soal : Diketahui sin α = 4/5 pada kuadran I tentukan nilai cot α dan cos α Jawab : 5 4 3 Cos α = 3/5 cot α = 3/4

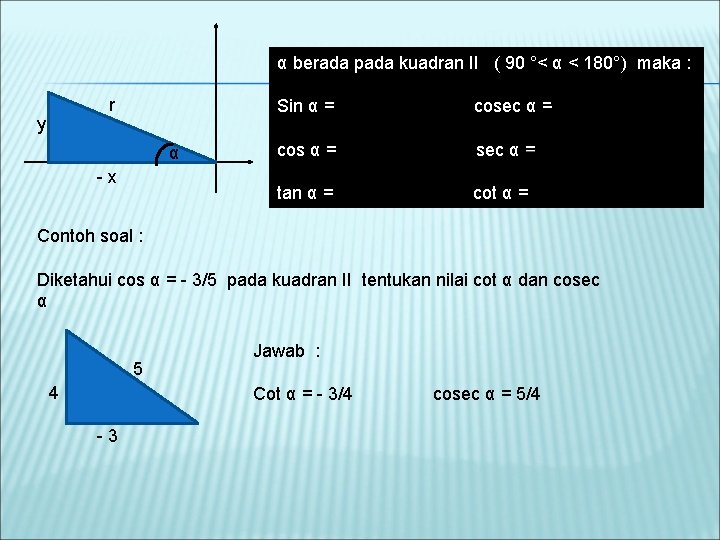
α berada pada kuadran II ( 90 °< α < 180°) maka : r y α -x Sin α = cosec α = cos α = sec α = tan α = cot α = Contoh soal : Diketahui cos α = - 3/5 pada kuadran II tentukan nilai cot α dan cosec α 5 4 Jawab : Cot α = - 3/4 -3 cosec α = 5/4

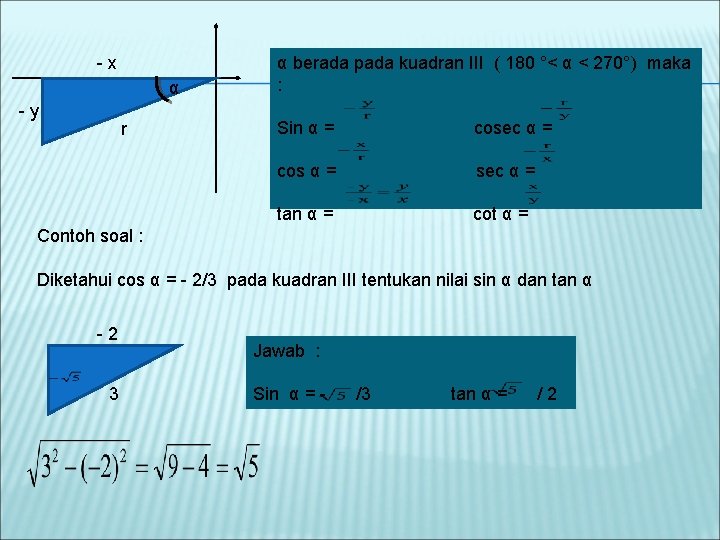
-x α -y r α berada pada kuadran III ( 180 °< α < 270°) maka : Sin α = cosec α = cos α = sec α = tan α = cot α = Contoh soal : Diketahui cos α = - 2/3 pada kuadran III tentukan nilai sin α dan tan α -2 3 Jawab : Sin α = - /3 tan α = /2

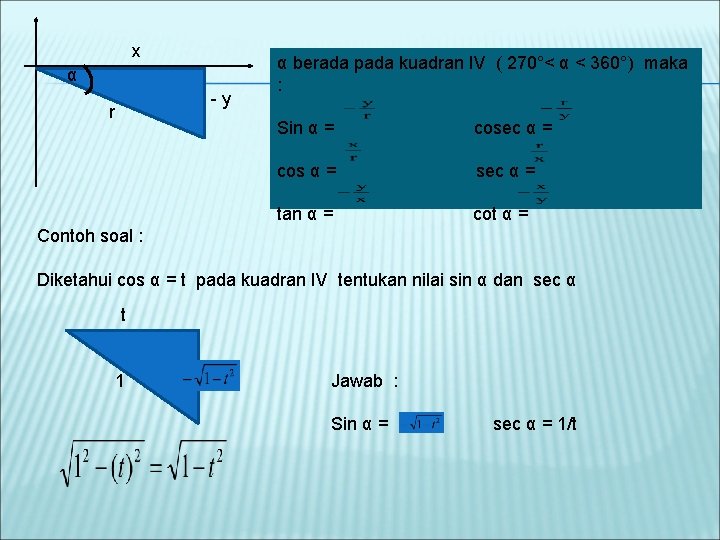
x α -y r α berada pada kuadran IV ( 270°< α < 360°) maka : Sin α = cosec α = cos α = sec α = tan α = cot α = Contoh soal : Diketahui cos α = t pada kuadran IV tentukan nilai sin α dan sec α t 1 Jawab : Sin α = sec α = 1/t

TIME OUT SENAM HOME

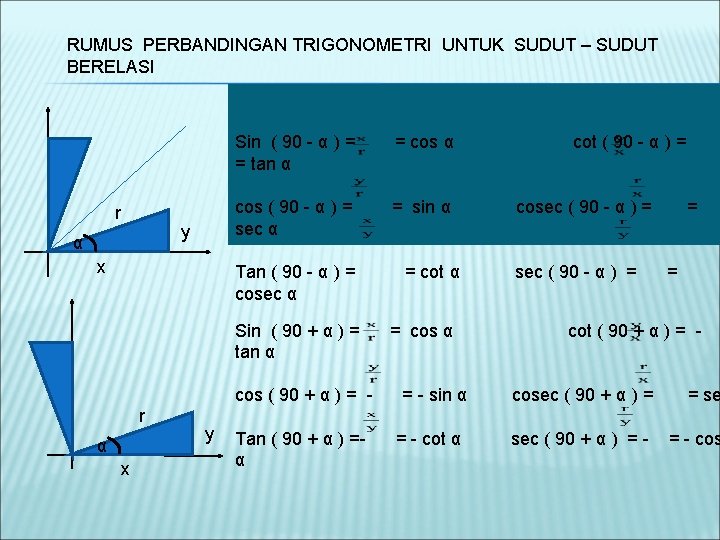
RUMUS PERBANDINGAN TRIGONOMETRI UNTUK SUDUT – SUDUT BERELASI r y α x Sin ( 90 - α ) = = tan α = cos α cos ( 90 - α ) = sec α = sin α Tan ( 90 - α ) = cosec α Sin ( 90 + α ) = tan α cos ( 90 + α ) = r α x y Tan ( 90 + α ) =α = cot α = cos α = - sin α = - cot α cot ( 90 - α ) = cosec ( 90 - α ) = = = cot ( 90 + α ) = cosec ( 90 + α ) = = se sec ( 90 + α ) = - cos

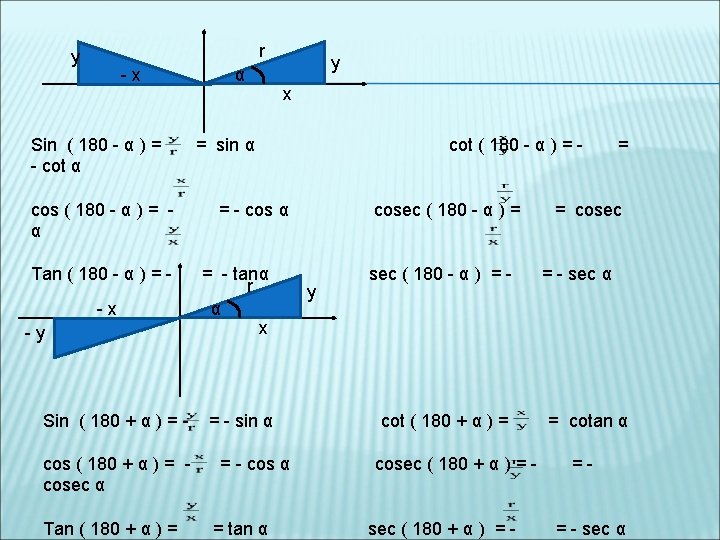
r y -x Sin ( 180 - α ) = - cot α cos ( 180 - α ) = α Tan ( 180 - α ) = -x -y Sin ( 180 + α ) = cosec α Tan ( 180 + α ) = α y x = sin α cot ( 180 - α ) = - cos α = - tanα r α x = - sin α = - cos α = tan α cosec ( 180 - α ) = y sec ( 180 - α ) = - cot ( 180 + α ) = cosec ( 180 + α ) = - = = cosec = - sec α = cotan α == - sec α

TIME OUT BERNYANYI HOME

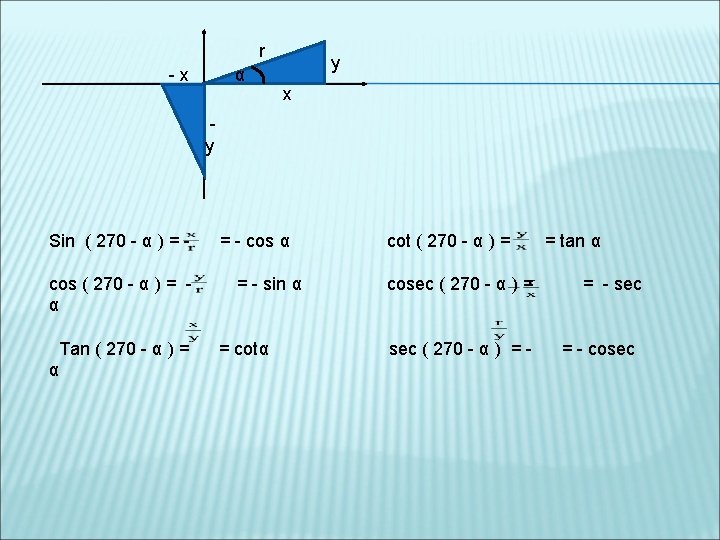
r -x α y x y Sin ( 270 - α ) = cos ( 270 - α ) = α Tan ( 270 - α ) = α = - cos α = - sin α = cotα cot ( 270 - α ) = cosec ( 270 - α ) = - = tan α = - sec = - cosec

Sin ( 270 + α ) = - cos α cot ( 270 + α ) = - tan α cos ( 270 + α ) = sin α cosec ( 270 + α ) = - sec α Tan ( 270 + α ) = - cotan α sec ( 270 + α ) = cosec α Sin ( 360 - α ) = - sin α cot ( 360 - α ) = - cot α cos ( 360 - α ) = cos α cosec ( 360 - α ) = - cosec α Tan ( 360 - α ) = - tan α sec ( 360 - α ) = sec α

LATIHAN : 1. Hitunglah nilai dari : a. Sin 315° b. Cos 210° c. Tan 240° 2. Sederhanakan bentuk berikut : a. b. 3. Diketahui sin 40°= n. Tentukan nilai dari tan 230° dan cot 320° BAC K

Rumus – rumus perbandingan trigonometri untuk sudut ( - α ) Sin ( - α ) = - sin α cot ( - α ) = - cot α cos ( - α ) = cos α cosec ( - α ) = - cosec α Tan ( - α ) = - tan α sec ( - α ) = sec α Rumus – rumus perbandingan trigonometri untuk sudut ( n. 360° - α ) Sin ( n. 360° - α ) = - sin α cos ( n. 360° - α ) = cos α Tan ( n. 360° - α ) = - tan α cot ( n. 360° - α ) = - cot α cosec (n. 360° - α ) = - cosec α sec ( n. 360° - α ) = sec α

Rumus – rumus perbandingan trigonometri untuk sudut ( n. 360° + α ) Sin ( n. 360° + α ) = sin α cot ( n. 360° + α ) = cot α coos ( n. 360°+α ) = cos α cosec (n. 360° + α ) = cosec α Tan ( n. 360° + α ) = tan α sec ( n. 360° + α ) = sec α BAC K

MERUBAH KEDUDUKAN TITIK DARI KOORDINAT KUTUB DALAM KOORDINAT KARTESIUS Cos α = x/r x = r. Cos α r y Sin α = y/r y = r. sin α Jadi A ( r , α ° ) = A ( r. cos α° , r. sin α° ) α x Contoh : 1. A ( 10 , 60° ) x = r. Cos α° ( 5, 5 ) = 10. Cos 60° = 10. ½ = 5 : 2. B ( 20 , 120° ) Contoh x = r. Cos α° 10 , 10 ) = 20. Cos 120° = 20. ( - ½ ) = - 10 y = r. sin α° jadi A = 10. Sin 60° = 10. ½ = 5 y = r. sin α° = 20. Sin 120° = 20. ½ = 10 jadi B ( BAC K

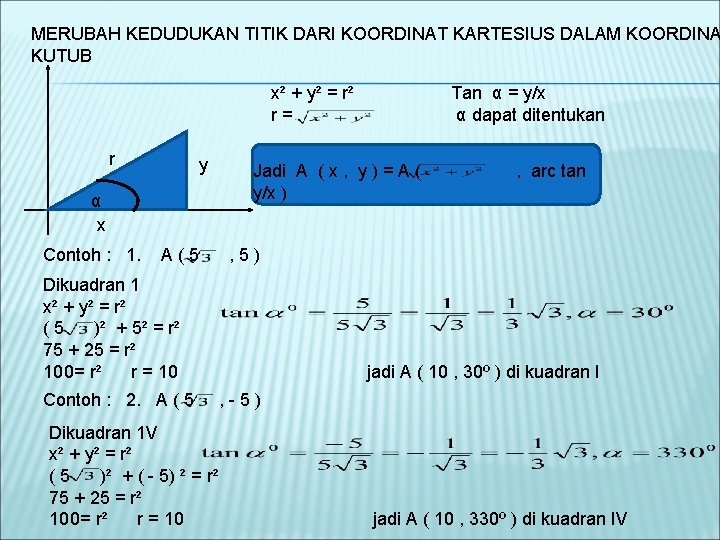
MERUBAH KEDUDUKAN TITIK DARI KOORDINAT KARTESIUS DALAM KOORDINA KUTUB x² + y² = r² r= r y α x Contoh : 1. A(5 Jadi A ( x , y ) = A ( y/x ) Dikuadran 1 V x² + y² = r² (5 )² + ( - 5) ² = r² 75 + 25 = r² 100= r² r = 10 , arc tan , 5) Dikuadran 1 x² + y² = r² (5 )² + 5² = r² 75 + 25 = r² 100= r² r = 10 Contoh : 2. A ( 5 Tan α = y/x α dapat ditentukan jadi A ( 10 , 30º ) di kuadran I , -5) jadi A ( 10 , 330º ) di kuadran IV

LATIHAN SOAL : 1. Nyatakan dalam koordinat kartesius a. A ( 10 , 315° ) b. B ( 5 , 225° ) 2. Nyatakan dalam koordinat kutub a. A ( - 1 , -1 ) b. B ( - 8 , 8 ) BAC K

IDENTITAS TRIGONOMETRI 1. Tan A = 5. cos²A + sin²A = 1 2. Cot A = 6. 1 + tan²A = sec²A 3. Sin A = 7. 1 + cot²A = cosec²A 4. cos A = 8. Tan² A = Contoh : Buktikan 1. Cos²A – sin²A = 2 cos²A- 1 5. Jika p – q = cos A = sin A 1 2. Cos²A – sin²A = 1 – 2 sin²A 3. Sin A. Cot A = cos A 4. = cosec A + cot A maka p² + q² = BAC K