Chemistry 2402 Thermodynamics Lecture 10 Phase Diagrams and










- Slides: 15

Chemistry 2402 - Thermodynamics Lecture 10 : Phase Diagrams and Solubility Lecture 11 : Solubility (cont. ) Lecture 12: Kinetic Coefficients for the Relaxation to Equilibrium

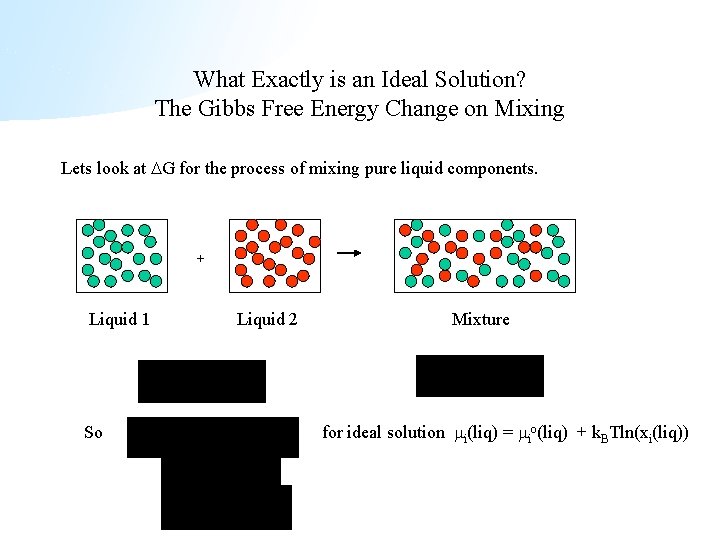
What Exactly is an Ideal Solution? The Gibbs Free Energy Change on Mixing Lets look at G for the process of mixing pure liquid components. + Liquid 1 So Liquid 2 Mixture for ideal solution i(liq) = io(liq) + k. BTln(xi(liq))

The Entropy of Mixing Since The we have i. e. Gmix = -T Smix so that Hmix = 0. This means that there is no energy change due to mixing – a defining feature of an ideal mixture. It turns out that Smix is maximised when all the species are present in equal amounts, i. e. all the xi’s are equal to each other

Freezing-point depression and boiling point elevation • The Gibbs free energy of mixing to form an ideal solution is always negative i. e. the solution is more stable than any of the pure liquids. • If the solute is a) nonvolatile, i. e. has an extremely low vapour pressure and b) is immiscible in the crystal phase of the solvent, then the solute will have lowered G for the liquid without significantly changing G for either gas or solid.

Example Problem The vapour pressure of benzene at 60 C is 51. 3 k. Pa. When 10 g of an unknown organic compound of negligible vapour pressure is dissolved in 30. 0 g of benzene, the pressure for liquid-gas coexistence is lowered to 44. 8 k. Pa. Assuming the solution can be treated as ideal, calculate the molar weight of the solute. Reminder – Raoult’s Law: An approximate relation was proposed by Raoult in 1880. He noted that, as long as the components in solution differed little from one another - e. g. benzene and toluene – then Pi(gas)= xi(liq)Pi* Raoult’s Law

Example Problem The vapour pressure of benzene at 60 C is 51. 3 k. Pa. When 10 g of an unknown organic compound of negligible vapour pressure is dissolved in 30. 0 g of benzene, the pressure for liquid-gas coexistence is lowered to 44. 8 k. Pa. Assuming the solution can be treated as ideal, calculate the molar weight of the solute. Applying Raoult’s Law, P = 51. 3 k. Pa xbenzene(liq). Therefore xbenzene = 44. 8/51. 3 = 0. 8733. The 30 g of benzene consisted of 0. 3846 mol. Now xbenzene = nbenzene/(nbenzene+ nunknown) Therefore 0. 8733 = 0. 3846/(0. 3846 + nunknown) and so nunknown= 0. 0558 mol. As this weighed 10 g, the molar mass is 179. 2 g mol-1. Reminder – Raoult’s Law: An approximate relation was proposed by Raoult in 1880. He noted that, as long as the components in solution differed little from one another - e. g. benzene and toluene – then Pi(gas)= xi(liq)Pi* Raoult’s Law

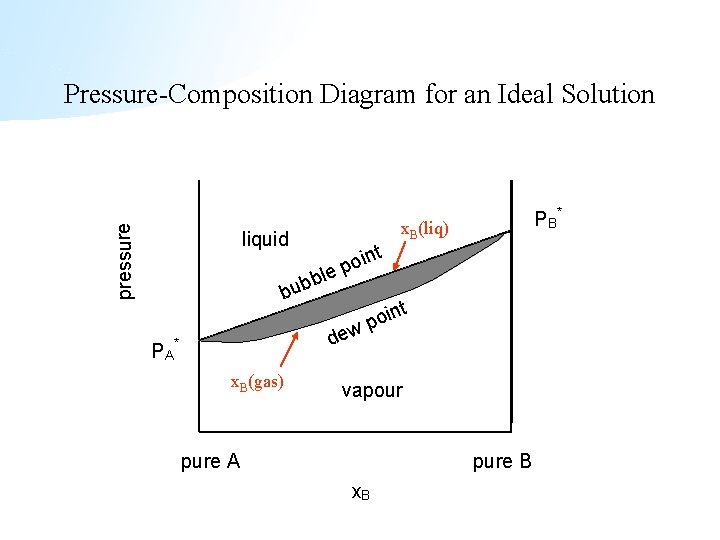
Pressure-Composition Diagram for an Ideal Solution Let’s consider a 2 component mixture of species A and B. From Raoult’s Law we have the pressure at liquid-vapour coexistence for a given liquid composition P = (1 -x. B(liq))PA* + x. B(liq)PB* (note that x. A(liq) = 1 -x. B(liq)) What is the composition of the gas at this pressure? x. B(gas) = PB/P = x. B(liq)PB*/P If PB* > PA* i. e. B is more volatile than A, then x. B(gas) > x. B(liq)

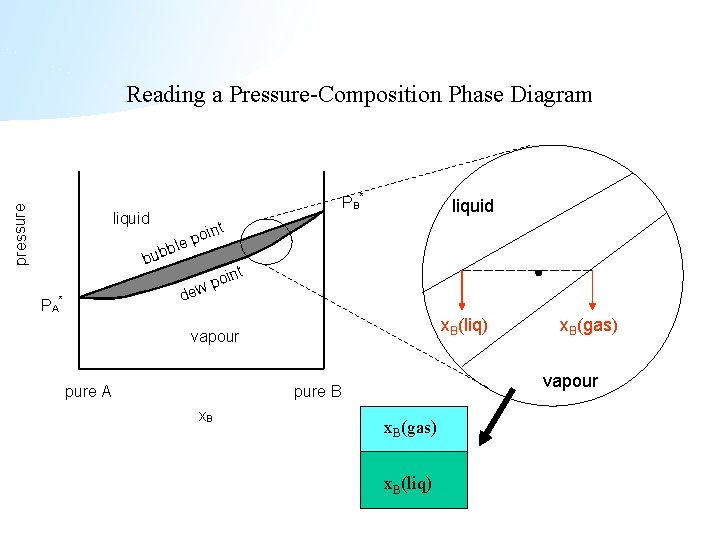
pressure Pressure-Composition Diagram for an Ideal Solution liquid b bub PA le t x. B(gas) x. B(liq) n poi t dew * P B* n poi vapour pure A pure B x. B

pressure Reading a Pressure-Composition Phase Diagram PB * liquid t oin p ble b u b t oin p dew PA * x. B(liq) vapour pure A vapour pure B x. B(gas) x. B(liq)

Example Problem At 353 K the vapour pressures of benzene and bromobenzene are 757 and 66 mm. Hg respectively. Assume the mixture obeys Raoult’s Law. For a mixture with the following composition [xbenzene(liq) = 0. 3 and xbromobenzene(liq) = 0. 7], i) calculate the pressure at which this mixture will begin to boil P = x. A(liq)PA* + x. B(liq)PB* = 757 × 0. 3 + 66 × 0. 7 = 273. 3 mm. Hg ii) calculate the mole fraction of benzene in the vapour phase at this pressure xbenzene(gas) = Pbenzene /P = (757 × 0. 3) / 273. 3 = 0. 83 the vapour is mostly benzene, where the solution was mostly bromobenzene!

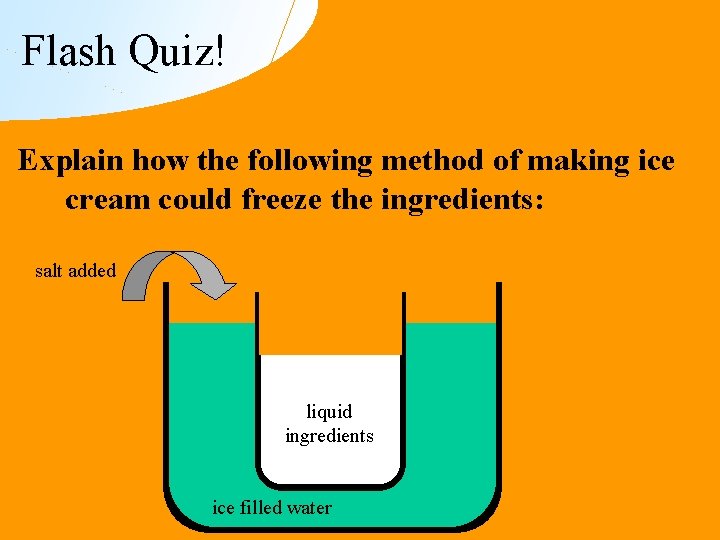
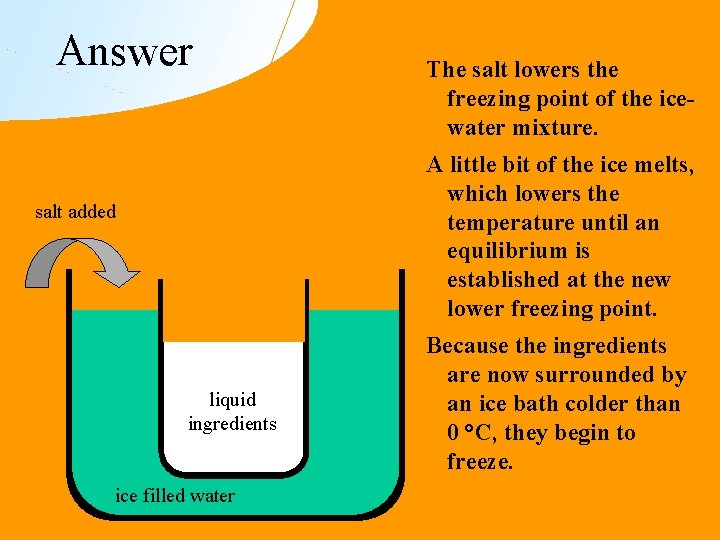
Flash Quiz! Explain how the following method of making ice cream could freeze the ingredients: salt added liquid ingredients ice filled water

Answer The salt lowers the freezing point of the icewater mixture. A little bit of the ice melts, which lowers the temperature until an equilibrium is established at the new lower freezing point. salt added liquid ingredients ice filled water Because the ingredients are now surrounded by an ice bath colder than 0 °C, they begin to freeze.

Saturated Solutions In a saturated solution, the solute is in equilibrium with it solid phase x. B(saturated solution) B(solid) = B(solution) Solid B at 1 atm we have Bo(solid) = Bo(liquid) + k. Tln(x. B(sat. sol. )) i. e. lnx. B(sat. sol. ) = ( Bo(solid)- Bo(liquid))/k. T lnx. B(sat. sol. ) = – Gomelt/RT since Gomelt = Goliquid – Gosolid = NAvogadro( Bo(liquid)- Bo(solid)) and R = k × NAvogadro So the solubility, x. B(sat. sol. ), of a solid into an ideal solution is directly related to the free energy of melting the solid, Gomelt ! For ideal solutions, solubility is simply a competition between the desire to freeze and the entropy of mixing. No account is made of the role of the solvent in stabilizing the dissolved species (which would be an important effect in non-ideal solutions).

Sample exam questions from previous years • At 40. 0 °C, heptane has a vapour pressure of 92. 45 mm. Hg, and octane has a vapour pressure of 31. 06 mm. Hg. In a 40 °C laboratory, a mixture is prepared in a sealed container, with 100. 0 g of liquid heptane and 60. 0 g of liquid octane. Assume this mixture obeys Raoult’s Law. – If the pressure of this system is reduced, at what pressure will it start to boil? • The vapour pressure of acetone at 30 C is 0. 3720 atm. When 15 g of an unknown organic compound of negligible vapour pressure is dissolved in 50. 0 g of acetone, the vapour pressure is lowered to 0. 3471 atm. Assuming the solution can be treated as ideal, calculate the molar weight of the solute.

Summary You should now • Be able to explain the concept of the entropy of mixing, and analyze it in the case of ideal solutions • Understand how the entropy of mixing is linked to the concepts of boiling point elevation and freezing point suppression • Be able to apply Raoult’s Law to relate the contents of an ideal solution to the contents of its equilibrium vapour • Draw and explain a pressure-composition diagram for an ideal mixture Next Lecture • Kinetic Coefficients for the Relaxation to Equilibrium