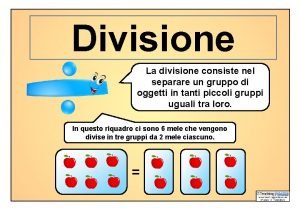
RICORSIONE ITERAZIONE Riconsideriamo lesempio del Massimo Comun Divisore

RICORSIONE & ITERAZIONE Riconsideriamo l’esempio del Massimo Comun Divisore visto tempo addietro: m, MCD(m, n) = se m=n MCD(m-n, n), se m>n MCD(m, n-m), se m<n

RICORSIONE & ITERAZIONE Questo esempio era stato trasposto nella funzione seguente: int mcd(int m, int n){ return (m==n) : m ? (m>n) ? mcd(m-n, n) : mcd(m, n-m); } L’esempio era particolare perché il risultato veniva sintetizzato in avanti, anziché all’indietro come nei processi ricorsivi.

RICORSIONE & ITERAZIONE · Ogni processo computazionale che computi “in avanti”, per accumulo, costituisce una ITERAZIONE ossia è un processo computazionale iterativo. · Ogni soluzione sintatticamente ricorsiva che dia luogo a un processo computazionale iterativo costituisce una ricorsione solo apparente: una ricorsione tail.

RICORSIONE & ITERAZIONE La caratteristica fondamentale di un processo computazionale ITERATIVO è che a ogni passo è disponibile un risultato parziale · dopo k passi, si ha a disposizione il risultato parziale relativo al caso k · questo non è vero nei processi computazionali ricorsivi, in cui nulla è disponibile finché non si è disgregato il problema fino al caso elementare.

IL RAGIONAMENTO ITERATIVO · Si basa sulla disponibilità di una variabile, detta accumulatore, destinata a esprimere in ogni istante la soluzione corrente · Si imposta identificando quell’operazione di modifica dell’accumulatore che lo porta a esprimere, dal valore relativo al passo k, il valore relativo al passo k+1.

ESEMPIO: CALCOLO DEL FATTORIALE Definizione: n! = 1 * 2 * 3 *… * n Detto vk = 1 * 2 * 3 *… * k: 1! = v 1 = 1 (k+1)! = vk+1 = (k+1) * vk n! = vn per k 1 per k=n

ESEMPIO: CALCOLO DEL FATTORIALE int fact(int n){ return fact. Iter(n, 1, 1); } int fact. Iter(int n, int v, int k){ return (k==n) ? v : fact. Iter(n, (k+1)*v, k+1); }

INVARIANTI Un invariante di programma è una relazione sempre vera in un dato punto del programma. Esempio: double power(double b, int k){ return (k<=0) ? 1 : power. It(b, k, b, 1); } Invariante di programma: è sempre vero che qui k>0

INVARIANTI DI CICLO Un invariante di ciclo è una relazione sempre vera, in un dato punto del programma, a ogni iterazione. • Identificare un invariante di ciclo è una forma di progetto. • Invarianti diversi suggeriscono di norma algoritmi diversi, che quasi sempre hanno diversa efficienza.

PROBLEMA: CALCOLO DI bk Un approccio iterativo Posto bk = vk, si può scrivere: b 0 = v 0 = 1 per i=0 bi = vi = b * bi-1 = b * vi-1 per i>0 in particolare: b k = vk per i=k Un possibile invariante: bk = vi * bk-i

PROBLEMA: CALCOLO DI bk Perché bk = bk-i *vi è un invariante? Al generico passo 0<i<k, bk = vi * bk-i Moltiplicando e dividendo per b: bk = (vi *b) * bk-i-1 = vi+1 * bk-(i+1) che è l’invariante al passo (i+1)-esimo. In particolare: • per i=0, bk = v 0 * bk = bk purché v 0 =1 • per i=k, bk = vk * b 0 = vk condizione iniziale

PROBLEMA: CALCOLO DI bk Come usarlo per progettare l’algoritmo? • inizialmente, v = v 0 =1 • a ogni passo si deve trasformare l’invariante bk = vi * bk-i nella forma bk = vi+1 * bk-(i+1) che deve assumere al passo successivo • ciò si ottiene ponendo, a ogni passo v’ = b * v i’ = i + 1

CALCOLO DI bk : L’INVARIANTE double power. It(double b, int k, double v, int i){ return (i==k) ? v : i’ = i+1 power. It(b, k, v*b, i+1); } V’ = Vi+1 = Vi* b double power(double b, int k){ return (k==0) ? 1 : power. It(b, k, 1, 0); } V 0=1 i=0

PROGETTARE bk PER INVARIANTI Partendo da relazioni diverse si ottengono approcci diversi, con diversa efficienza. Un diverso invariante: • k=0 • k>0 k pari k dispari b*b: non richiede di saper fare potenze b 0 = 1 bk = (b 2) k/2 bk = b * bk-1 richiede di saper fare un prodotto

PROGETTARE bk PER INVARIANTI Come usarlo per progettare l’algoritmo? • a ogni passo si deve riscrivere bk in una delle due forme date • ciò si ottiene ponendo, a ogni passo – se k è pari: – se k è dispari: b’ = b * b k’ = k/2 b’ = b k’ = k-1 e moltiplicando per b richiede una operazione dopo la fase di modifica di b e k soluzione ricorsiva

PROGETTARE bk PER INVARIANTI boolean odd(int n){ return n%2==1; } double pow(double b, int k){ ricorsione non-tail return (k==0) ? 1 : odd(k) ? pow(b, k-1) * b : pow(b*b, k/2); } (Complessità dell’ordine di log 2 k)

PROGETTARE bk PER INVARIANTI UN APPROCCIO ITERATIVO Un ulteriore invariante: • k=0 n=0, t=1 • k>0 – se n è pari: – se n è dispari: b k = t * vn bk = t * v 0 = 1 bk = t * (v 2) n/2 bk = t * vn-1

PROGETTARE bk PER INVARIANTI Progetto dell’algoritmo: • a ogni passo si deve trasformare l’invariante bk = t * vn in una delle due forme date • ciò si ottiene ponendo: – se n è pari – se n è dispari v’ = v n’ = n/2, t’ = t, v’ = v 2 n’ = n-1, t’ = t*v, Interessante: b e k in realtà non si usano!

PROGETTARE bk PER INVARIANTI boolean odd(int n){return n%2==1; } double pow. It(double b, int k, double t, double v, int n){ return (n==0) ? t : odd(n) ? pow. It(b, k, t*v, v, n-1) : pow. It(b, k, t, v*v, n/2); } Come previsto, b e k non servono! Quindi li possiamo togliere…!!

PROGETTARE bk PER INVARIANTI boolean odd(int n){return n%2==1; } double pow. It(double t, double v, int n){ return (n==0) ? t : odd(n) ? pow. It(t*v, v, n-1) : pow. It(t, v*v, n/2); } double power(double b, int k){ return (k==0) ? 1 : pow. It(1, b, k); }

ESERCIZIO: MOLTIPLICAZIONE Obiettivo: calcolare p = x* y Sfruttiamo l’invariante: y=Q*B+R dove • B è un intero positivo • Q (quoziente) = y/B • R (resto) = y%B

ESERCIZIO: MOLTIPLICAZIONE Obiettivo: calcolare p = x* y Sostituendo: p = x * y = x* (Q * B + R) = = x * (B * (y/B)) + x*(y%B) Caso particolare: y=0 p = x * y = x*0 = 0

ESERCIZIO: MOLTIPLICAZIONE Approccio ricorsivo: si applica direttamente la relazione trovata p = x*B * (y/B) ) + x*(y%B) Ad esempio, scegliendo B=2: int Mul. Nat. R(int x, int y){ return (y==0) ? 0 : Mul. Nat. R(x*2, y/2) + x*(y%2); } Occorre fare un’operazione dopo la chiamata ricorsiva ricorsione non-tail

ESERCIZIO: MOLTIPLICAZIONE Approccio ricorsivo: si applica direttamente la relazione primitiva che suppotrovata p = x*B Operazione * (y/B) ) + x*(y%B) niamo di saper già fare (è una Ad esempio, scegliendo B=2: moltiplicazione per 0 o per 1) int Mul. Nat. R(int x, int y){ return (y==0) ? 0 : Mul. Nat. R(x*2, y/2) + x*(y%2); } Operazioni primitive che supponiamo di saper già fare (moltiplicazione/divisione per 2)

ESERCIZIO: MOLTIPLICAZIONE Verso un approccio iterativo Cerchiamo un invariante di ciclo p=x*y+z Ponendo y=Q*B+R e trasformando: p = (x*B) * Q + (x*R + z) = x’ * y’ + z’ dove si è posto y’ = Q = y/B, x’ = x*B, z’ = z + x*R Caso particolare: y=0 p = z

ESERCIZIO: MOLTIPLICAZIONE Invariante di ciclo: p = x * y + z Trasformazione: p = x’ * y’ + z’ y’ = Q = y/B, x’ = x*B, z’ = z + x*R int Mul. Nat. It(int x, int y, int z){ return(y==0) ? z : Mul. Nat. It(x*2, y/2, z+x*(y%2)); } Operazioni primitive: supponiamo di saper già moltiplicare, dividere e modulare per 2.

ESERCIZIO: MOLTIPLICAZIONE Perché supponiamo di saper già moltiplicare, e dividere per 2 (trovando anche il resto) ? Perché l’elaboratore è intrinsecamente capace di farlo nella propria ALU: • moltiplicazione per 2 = shift a sinistra (<<) • divisione per 2 = shift a destra (>>) • moltiplicazione per (y%2) = 0, se y è pari (y%2 vale 0) y, se y dispari (y%2 vale 1)

ESERCIZIO: MOLTIPLICAZIONE Il codice finale che ne risulta: int Mul. Nat. It(int x, int y, int z){ return (y==0) ? z : odd(y): Mul. Nat. It(x<<1, y>>1, z+x) : Mul. Nat. It(x<<1, y>>1, z); y%2 = 1 } x/2 y%2 = 0 boolean odd(int n){return n%2==1; }

UNA RIFLESSIONE DI FONDO • L’impostazione funzionale è sempre costruttiva. Ma si può sempre solo creare? • Perché creare una versione nuova di un accumulatore ad ogni passo, quando l’elaboratore di Von Neumann permette la modifica del contenuto di una cella di memoria?

UNA PROPOSTA • È possibile riusare una stessa area dati senza bisogno di crearne una nuova ad ogni passo computazionale? • Ci sono controindicazioni?

VARIABILI NEI LINGUAGGI IMPERATIVI Una variabile in un linguaggio imperativo · non è solo un sinonimo per un dato come in matematica · è un’astrazione della cella di memoria · associata a due diverse informazioni: · il contenuto (R-value) · l’indirizzo a cui si trova (L-value) x 3. 22 a

ESPRESSIONI CON EFFETTI COLLATERALI · Le espressioni che contengono variabili, oltre a denotare un valore, possono a volte comportare effetti collaterali sulle variabili coinvolte. · Un effetto collaterale è una modifica del valore della variabile (R-value) causato da particolari operatori: · operatore di assegnamento · operatori di incremento e decremento

ASSEGNAMENTO • L’assegnamento è un particolare tipo di espressione – come tale denota comunque un valore!! con un effetto collaterale: quello di cambiare il valore della variabile. • Sintassi variabile = espressione • Esempi di espressioni di assegnamento: j=0 k=j+1

ASSEGNAMENTO L’espressione di assegnamento variabile = espressione · denota il valore dell’ espressione · ma cambia anche il valore della variabile: il nuovo valore della variabile è quello denotato dalla espressione.

ESEMPIO Se k valeva 2, l’espressione k=7 · denota il valore 7 · e cambia il valore di k, che d’ora in poi vale 7 (non più 2)

ESEMPIO Se k valeva 2, l’espressione j = k+1 · denota il valore 3 · e cambia il valore di j, che d’ora in poi vale 3 (qualunque valore avesse prima) L’assegnamento è distruttivo

ESPRESSIONI DI ASSEGNAMENTO Il valore denotato dall’espressione di assegnamento può essere usato in altre espressioni. Ad esempio, 3 + (k=7) · denota il valore 10 · e cambia in 7 il valore di k

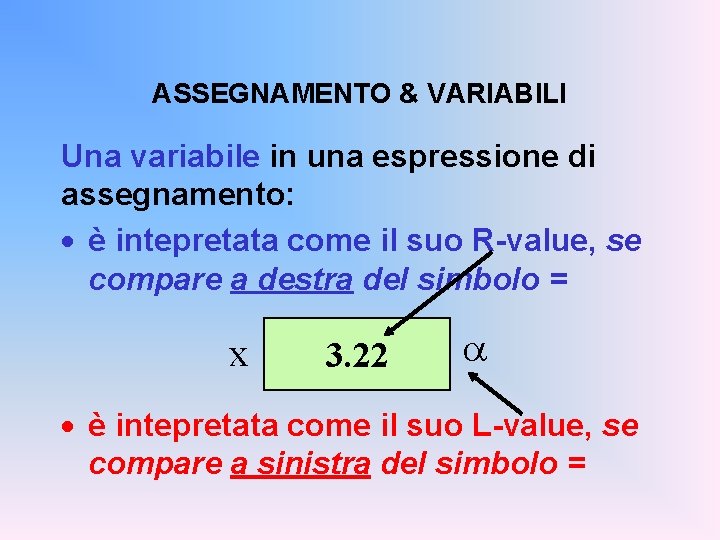
ASSEGNAMENTO & VARIABILI Una variabile in una espressione di assegnamento: · è intepretata come il suo R-value, se compare a destra del simbolo = x 3. 22 a · è intepretata come il suo L-value, se compare a sinistra del simbolo =

ESEMPIO Se x valeva 2, l’espressione x=x+1 · denota il valore 3 · e cambia in 3 il valore di x · il simbolo x a destra dell’operatore = denota il valore attuale (R-value) di x, cioè 2 · il simbolo x a sinistra dell’operatore = denota la cella di memoria associata a x (L-value), a cui viene assegnato il valore dell’espressione di destra (3) · l’espressione nel suo complesso denota il valore della variabile dopo la modifica, cioè 3.

ASSEGNAMENTO: ASSOCIATIVITÀ • Come tutti gli operatori, anche l’operatore di assegnamento deve avere una sua associatività k=j=1 Prima k=j, o prima j=1 ? · l’operatore di assegnamento è associativo a destra: ciò consente espressioni di assegnamento multiplo

ASSEGNAMENTO: ASSOCIATIVITÀ Esempi k=j=1 interpretato come k = (j = 1) i = j = k = 0 interpretato come i = (j = (k=0)) i=k+5=6 NO: k+5 non ha un L-value! Nota: anche volendo, sarebbe stato impossibile farlo associativo a sinistra, in quanto ciò avrebbe reso molte espressioni prive di significato. Ad esempio: k=j=2 interpretato come (k=j) = 2 ? ? ? Equivarrebbe a scrivere 1 = 2 !!!!

INCREMENTO (++) E DECREMENTO (--) Gli operatori di incremento e decremento sono usabili in due modi • come pre-operatori: ++v prima incremento, poi uso • come post-operatori: v++ prima uso, poi incremento

ESEMPI int i, j, k = 5; i = ++k /* i vale 6, k vale 6 i = k++ /* i vale 5, k vale 6 */ */ int i=4, j, k = 5; j = i + k++; /* j vale 9, k vale 6 */ j = ++k - k++; /* in cerca di guai! */

ATTENZIONE…!! int k = 6; j = ++k - k++; /* in cerca di guai! */ Detti x = ++k e y = k++, • è certo che l’espressione venga valutata come j = x - y (da sinistra a destra) • è certo che alla fine k valga 8 • ma non si sa se venga calcolato prima x o prima y, e qui la cosa fa molta differenza! – se prima x, poi y j = 7 - 7 = 0 – se prima y, poi x j = 8 - 6 = 2

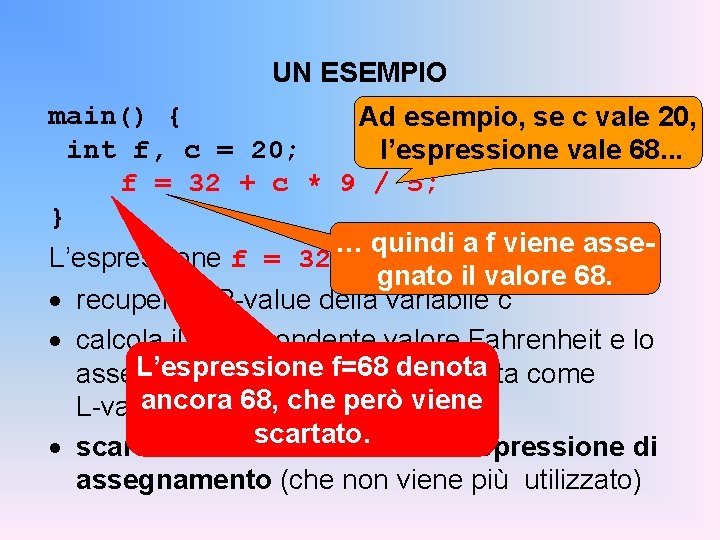
UN ESEMPIO main() { Ad esempio, se c vale 20, int f, c = 20; l’espressione vale 68. . . f = 32 + c * 9 / 5; } … quindi a f viene asse. L’espressione f = 32 + c * 9 / 5 gnato il valore 68. · recupera l’ R-value della variabile c · calcola il corrispondente valore Fahrenheit e lo L’espressione denota come assegna alla variabilef=68 f (interpretata ancora 68, che però viene L-value effetto collaterale) scartato. · scarta il valore denotato dall’espressione di assegnamento (che non viene più utilizzato)

ISTRUZIONI • Le istruzioni esprimono azioni che, una volta eseguite, comportano una modifica permanente dello stato interno del programma o del mondo circostante. • Le strutture di controllo permettono di aggregare istruzioni semplici in istruzioni più complesse.

ISTRUZIONI • Una istruzione C è espressa dalle seguenti produzioni: <istruzione> : : = <istruzione-semplice> <istruzione> : : = <istruzione-di-controllo> <istruzione-semplice> : : = <espressione> ; • Quindi, qualsiasi espressione seguita da un punto e virgola è una istruzione semplice.

ESEMPI DI ISTRUZIONI SEMPLICI x = 0; y = 1; x = 0, y = 1; k++; 3; ; /* due istruzioni */ /* una istruzione */ /* non fa nulla */ /* istruz. vuota*/

ISTRUZIONI DI CONTROLLO Una istruzione di controllo può essere: • una istruzione composta (blocco) • una istruzione condizionale (selezione) • una istruzione di iterazione (ciclo) come specificato dalla produzione: < istruzione-di-controllo > : : = <blocco> | <selezione> | <iterazione>

ISTRUZIONI DI CONTROLLO Le istruzione di controllo sono alla base della programmazione strutturata (Dijkstra, 1969). Concetti chiave: • concatenazione o composizione • selezione o istruzione condizionale ramifica il flusso di controllo in base al valore vero o falso di una espressione (“condizione di scelta”) • ripetizione o iterazione esegue ripetutamente un’istruzione finché rimane vera una espressione (“condizione di iterazione”)

TEOREMA DI JACOPINI-BÖHM • Le strutture di concatenazione, iterazione e selezione costituiscono un insieme completo in grado di esprimere tutte le funzioni calcolabili. • Dunque, l’uso di queste sole strutture di controllo non limita il potere espressivo. • La dimostrazione del teorema è basata sulla Turing-equivalenza di un “mini-linguaggio” che fornisca solo tali strutture di controllo.

BLOCCO <blocco> : : = { [ <dichiarazioni e definizioni> ] { <istruzione> } } Lo scope dei simboli che compaiono entro il blocco è il blocco stesso • dopo un blocco non occorre il punto e virgola (esso termina le istruzioni semplici, non separa istruzioni)

ESEMPIO DI BLOCCO main() { /* INIZIO BLOCCO */ const float F 1=9. 0, F 2=5, SH=32; int c, f, temp = 20; char scala = 'C'; c = (scala != 'F') ? temp : (F 2 / F 1 * (temp - SH)) ; f = (scala != 'F') ? (SH+temp*F 1/F 2) : temp; } /* FINE BLOCCO */

. . una nota “en passant”. . . main() { /* INIZIO BLOCCO */ const float F 1=9. 0, F 2=5, SH=32; int c, f, temp = 20; char scala = 'C'; Il qualificatore const rende c = (scala != 'F') ? temp queste : variabili (F 2 / non F 1 modificabili * (temp - SH)) ; f = (scala != 'F') ? (SH+temp*F 1/F 2) : temp; } /* FINE BLOCCO */

ESEMPIO DI BLOCCHI ANNIDATI main() { /* INIZIO BLOCCO ESTERNO */ const float F 1=9. 0, F 2=5, SH=32; int c, f, temp = 20; { /* INIZIO BLOCCO INTERNO */ char scala = ‘C’; c = (scala != 'F') ? temp : (F 2 / F 1 * (temp - SH)) ; f = (scala != 'F') ? (SH+temp*F 1/F 2) : temp; } /* FINE BLOCCO INTERNO */ } /* FINE BLOCCO ESTERNO */

ISTRUZIONI CONDIZIONALI <selezione> : : = <scelta> | <scelta-multipla> • la seconda non è essenziale, ma migliora l’espressività. • l’espressione condizionale ternaria (. . ? … : …) fornisce già un mezzo per fare scelte, ma è poco leggibile in situazioni di medio/alta complessità. L’istruzione di scelta fornisce un altro modo per esprimere alternative.

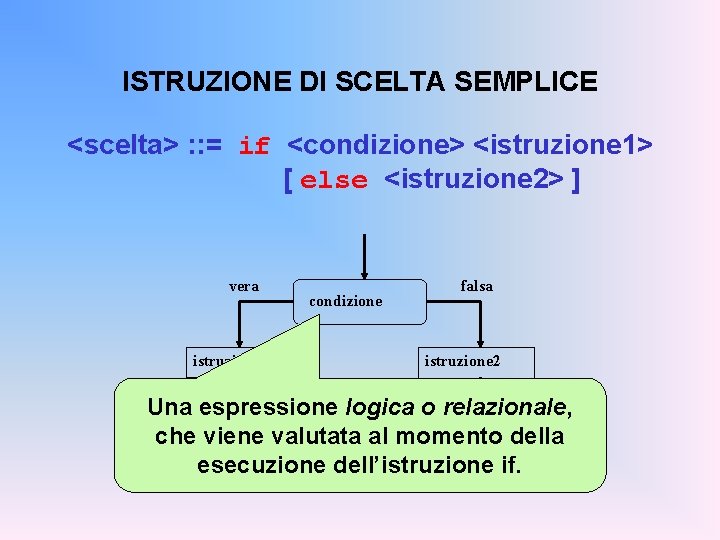
ISTRUZIONE DI SCELTA SEMPLICE <scelta> : : = if <condizione> <istruzione 1> [ else <istruzione 2> ] vera istruzione 1 condizione falsa istruzione 2 Una espressione logica o relazionale, che viene valutata al momento della esecuzione dell’istruzione if.

ISTRUZIONE DI SCELTA SEMPLICE <scelta> : : = if <condizione> <istruzione 1> [ else <istruzione 2> ] La parte else è opzionale: se omessa, in vera caso di condizione falsa si passa subito all’istruzione che segueistruzione 1 l’if. falsa istruzione 2

ESEMPIO DI ISTRUZIONE if • <istruzione 1> e <istruzione 2> sono ciascuna singola istruzione • Qualora occorra specificare più istruzioni, si deve quindi utilizzare un blocco. if (n > 0) { /* inizio blocco */ a = b + 5; c = (x<3) ? a : b; } /* fine blocco */ else n = b;

ISTRUZIONE if ANNIDATE • Come caso particolare, <istruzione 1> o <istruzione 2> potrebbero essere un altro if • Occorre attenzione ad associare le parti else Regola semantica: (che sono opzionali) all’ if corretto l’else è sempre associato all’if più interno if (n > 0) if (a>b) n = a; Se ciò non soddisfa occorelse n = b; /* riferito a if(a>b) */ re inserire esplicitamente un blocco. if (n > 0) { if (a>b) n = a; } else n = b; /* riferito a if(n>0) */

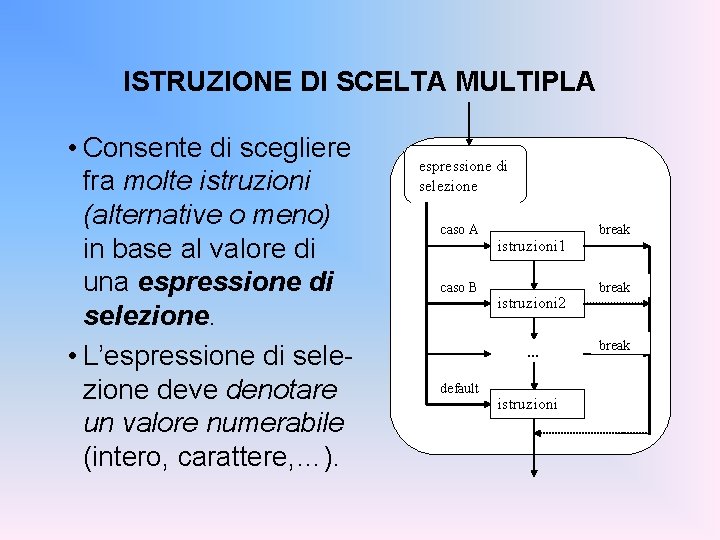
ISTRUZIONE DI SCELTA MULTIPLA • Consente di scegliere fra molte istruzioni (alternative o meno) in base al valore di una espressione di selezione. • L’espressione di selezione deve denotare un valore numerabile (intero, carattere, …). espressione di selezione caso A caso B istruzioni 1 istruzioni 2 … default istruzioni break

ISTRUZIONE DI SCELTA MULTIPLA <scelta-multipla> : : = Se nessuna etichetta corriswitch (selettore) { sponde, si prosegue col il ramo default. case <etichetta 1> : < istruzioni> [ break; ] case <etichetta 2> : < istruzioni> [ break; ] … [ default : < istruzioni> ] } Se neanche quello esiste, Il valore dell’espressione selettore viene confronsi prosegue con l’istruzione tato con le etichette dei vari casi: l’esecuzione successiva allo switch. prosegue dal ramo corrispondente (se esiste).

ISTRUZIONE DI SCELTA MULTIPLA Le etichette sono costanti <scelta-multipla> : : = switch (selettore) { dello stesso tipo del selettore. case <etichetta 1> : < istruzioni> [ break; ] case <etichetta 2> : < istruzioni> [ break; ] … [ default : < istruzioni> ] Attenzione: <istruzioni> } denota una sequenza di Il valore dell’espressione selettoreistruzioni viene confronoccorre un blocco) tato con le etichette dei vari(non casi: l’esecuzione prosegue dal ramo corrispondente (se esiste).

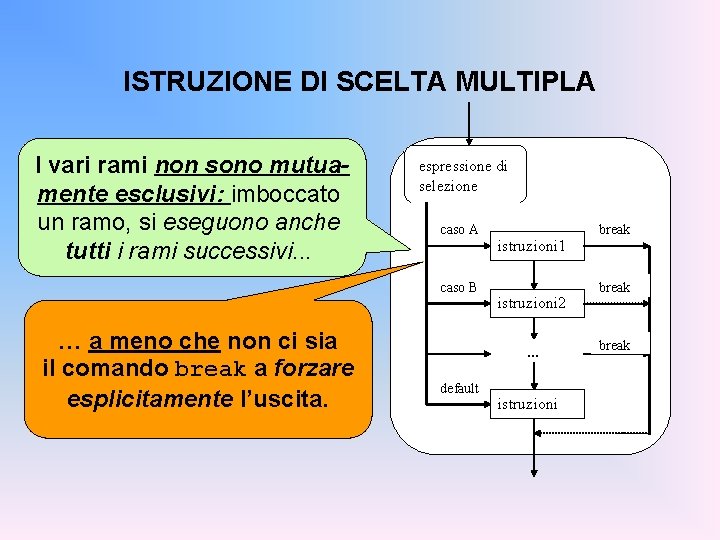
ISTRUZIONE DI SCELTA MULTIPLA I vari rami non sono mutuamente esclusivi: imboccato un ramo, si eseguono anche tutti i rami successivi. . . espressione di selezione caso A caso B … a meno che non ci sia il comando break a forzare esplicitamente l’uscita. istruzioni 1 istruzioni 2 … default istruzioni break

ISTRUZIONI DI ITERAZIONE <iterazione> : : = <while> | <for> | <do-while> • Per il Teorema di Jacopini-Böhm, una struttura di controllo iterativa sarebbe sufficiente: averne di più migliora l’espressività del linguaggio. • Le istruzioni di iterazione: · hanno un solo punto di ingresso e un solo punto di uscita nel flusso del programma · perciò possono essere interpretate come una singola azione in una computazione sequenziale.

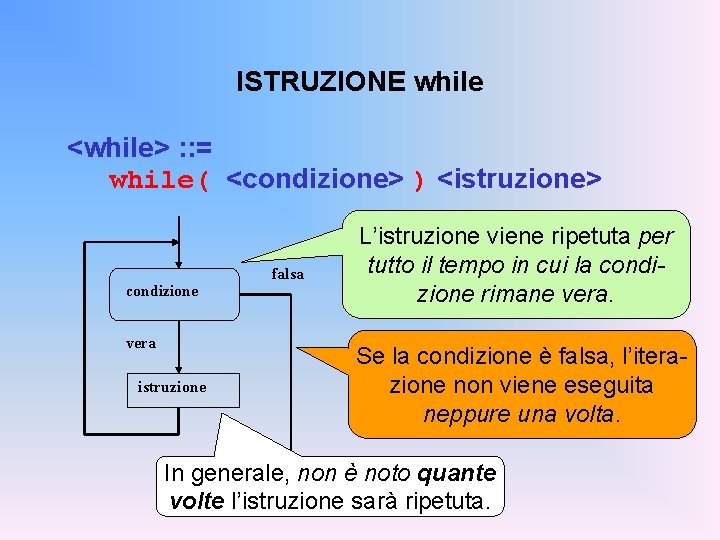
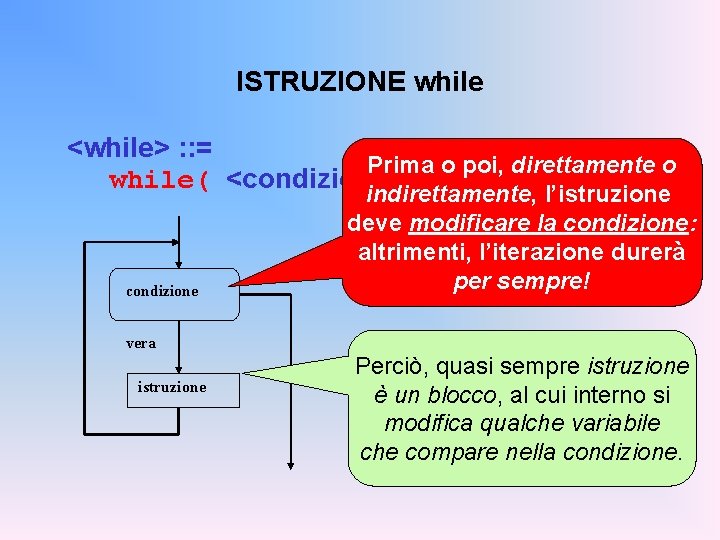
ISTRUZIONE while <while> : : = while( <condizione> ) <istruzione> condizione vera istruzione falsa L’istruzione viene ripetuta per tutto il tempo in cui la condizione rimane vera. Se la condizione è falsa, l’iterazione non viene eseguita neppure una volta. In generale, non è noto quante volte l’istruzione sarà ripetuta.

ISTRUZIONE while <while> : : = Prima o poi, direttamente o while( <condizione> ) <istruzione> condizione falsa indirettamente, l’istruzione deve modificare la condizione: altrimenti, l’iterazione durerà per sempre! vera istruzione Perciò, quasi sempre istruzione è un blocco, al cui interno si modifica qualche variabile che compare nella condizione.

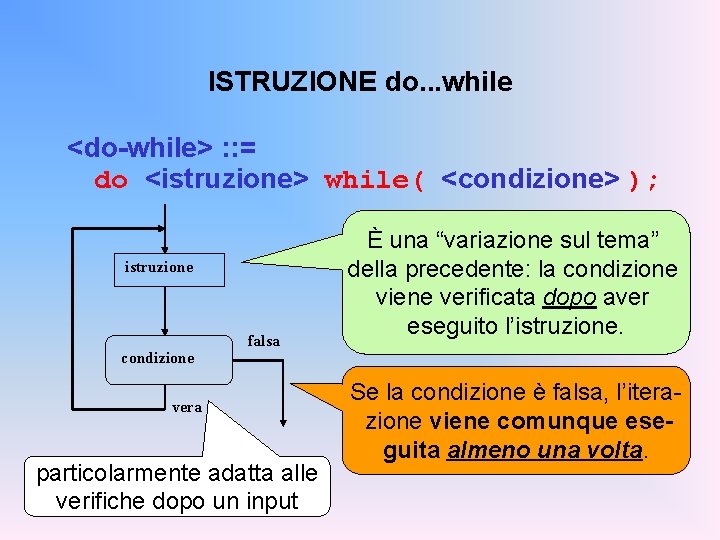
ISTRUZIONE do. . . while <do-while> : : = do <istruzione> while( <condizione> ); istruzione condizione falsa vera particolarmente adatta alle verifiche dopo un input È una “variazione sul tema” della precedente: la condizione viene verificata dopo aver eseguito l’istruzione. Se la condizione è falsa, l’iterazione viene comunque eseguita almeno una volta.

ISTRUZIONE for È una evoluzione dell’istruzione while rispetto a cui mira a eliminare alcune frequenti sorgenti di errore: · mancanza delle necessarie inizializzazioni delle variabili · mancanza della fase di modifica del ciclo (rischio di ciclo senza fine)

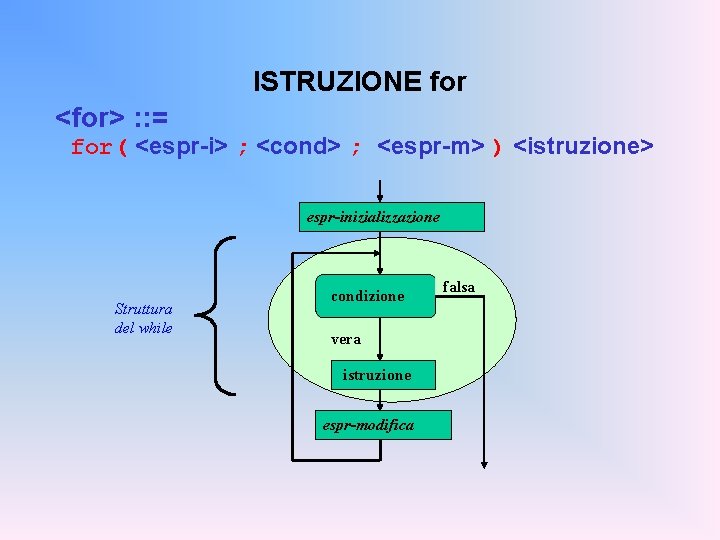
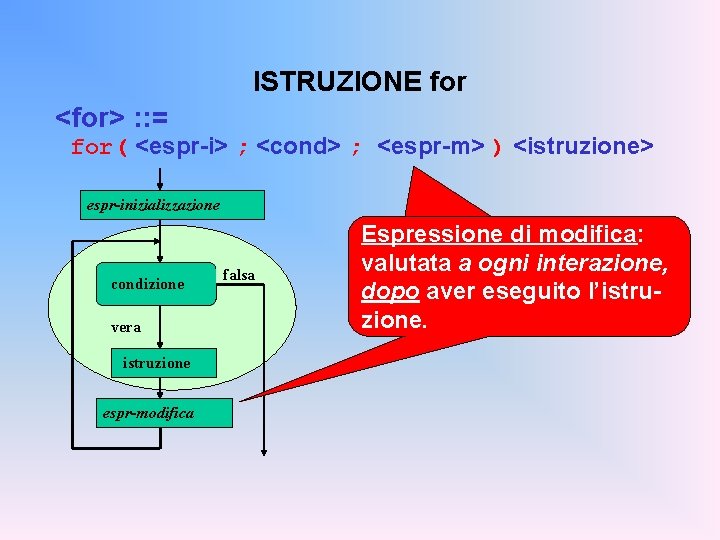
ISTRUZIONE for <for> : : = for( <espr-i> ; <cond> ; <espr-m> ) <istruzione> espr-inizializzazione Struttura del while condizione vera istruzione espr-modifica falsa

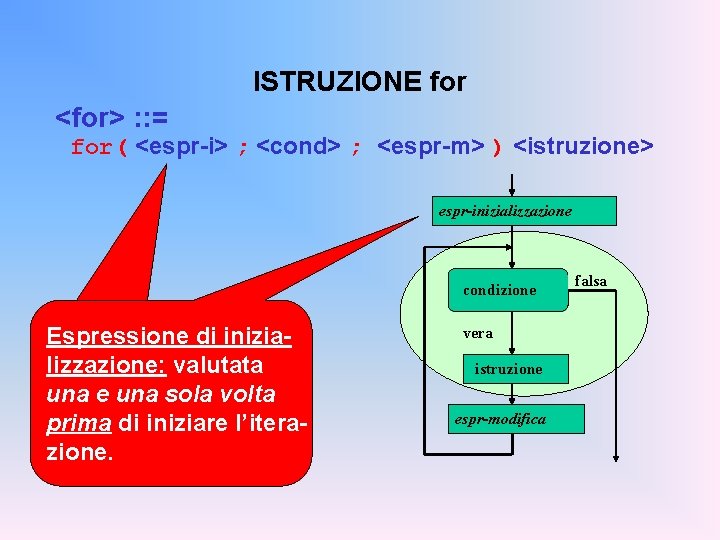
ISTRUZIONE for <for> : : = for( <espr-i> ; <cond> ; <espr-m> ) <istruzione> espr-inizializzazione condizione Espressione di inizializzazione: valutata una e una sola volta prima di iniziare l’iterazione. vera istruzione espr-modifica falsa

ISTRUZIONE for <for> : : = for( <espr-i> ; <cond> ; <espr-m> ) <istruzione> espr-inizializzazione condizione vera istruzione espr-modifica falsa Condizione: valutata a ogni interazione, per decidere se proseguire (come in un while) Se manca si assume vera!

ISTRUZIONE for <for> : : = for( <espr-i> ; <cond> ; <espr-m> ) <istruzione> espr-inizializzazione condizione vera istruzione espr-modifica falsa Espressione di modifica: Condizione: valutata a ogni interazione, per decidere dopo aver eseguito se proseguire l’istru(come in un while) zione.

UN ESEMPIO Il solito problema: calcolo del fattoriale • Dall’approccio ricorsivo… • . . . all’approccio sintatticamente ricorsivo, ma computazionalmente iterativo (ricorsione tail). . . • . . . all’approccio iterativo tramite istruzioni di iterazione.

IL FATTORIALE ITERATIVO TRAMITE ESPRESSIONE CONDIZIONALE. . . int fact. Iter(int n, int i, int v){ /* inizialmente, v = 1 */ /* invariante di ciclo: v = i! */ return (i==n) ? v : fact. Iter(n, i+1, (i+1)*v); } Chiamata: fact. Iter(n, 0, 1)

. . . IL FATTORIALE ITERATIVO TRAMITE ISTRUZIONE CONDIZIONALE. . . int fact. Iter(int n, int i, int v){ /* inizialmente, v = 1 */ /* invariante di ciclo: v = i! */ if (i==n) return v; else return fact. Iter(n, i+1, (i+1)*v); } Chiamata: fact. Iter(n, 0, 1)

. . . IL FATTORIALE ITERATIVO TRAMITE ISTRUZIONE DI ITERAZIONE: while int fact(int n){ int v=1; int i=0; while (i<n) { v = (i+1)*v; i = i+1; } return v; } /* inizialmente, v = 1 */ /* inizialmente, i = 0 */ /* invariante: v = i! */ I valori iniziali, prima forniti dll’esterno, divengono ora variabili locali della funzione interfaccia utente più pulita

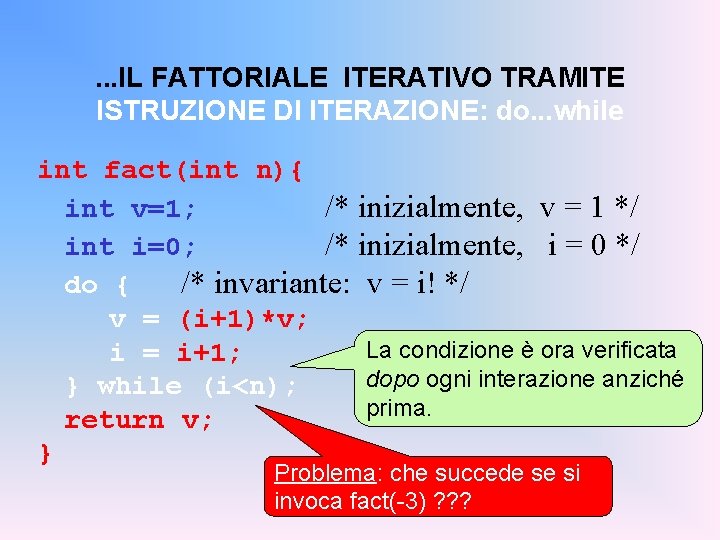
. . . IL FATTORIALE ITERATIVO TRAMITE ISTRUZIONE DI ITERAZIONE: do. . . while int fact(int n){ int v=1; /* inizialmente, v = 1 */ int i=0; /* inizialmente, i = 0 */ do { /* invariante: v = i! */ v = (i+1)*v; La condizione è ora verificata i = i+1; dopo ogni interazione anziché } while (i<n); prima. return v; } Problema: che succede se si invoca fact(-3) ? ? ?

. . . IL FATTORIALE ITERATIVO TRAMITE ISTRUZIONE DI ITERAZIONE: for int fact(int n){ int v=1; /* inizialmente, v = 1 */ int i; for (i=0; i<n; i=i+1) v = (i+1)*v; /* invariante: v = i! */ return v; } Le fasi di inizializzazione e di modifica della variabile di controllo del ciclo sono ben in evidenza nella struttura del for.

ITERAZIONE & RICORSIONE TAIL Poiché la ricorsione tail dà luogo a un processo computazionale di tipo iterativo, deve essere possibile trasformare un ciclo in ricorsione tail e viceversa. COME FARLO? · il corpo del ciclo rimane immutato · il ciclo diventa un if con, in fondo, la chiamata tail-ricorsiva.

ITERAZIONE & RICORSIONE TAIL • il corpo del ciclo rimane immutato • il ciclo diventa un if con, in fondo, la chiamata tail-ricorsiva. Naturalmente, può essere necessario aggiungere nuovi parametri nell’intestazione della funzione tailricorsiva, per “portare avanti” le variabili di stato.

ESEMPIO: Massimo Comun Divisore La soluzione tail-ricorsiva già vista. . . int mcd(int m, int n){ if (m!=n) if (m>n) return mcd(m-n, n); else return mcd(m, n-m); else return m; } … opportunamente riscritta. . . int mcd(int m, int n){ if (m!=n) { if (m>n) m=m-n; else n=n-m; return mcd(m, n); } else return m; }

ESEMPIO: Massimo Comun Divisore … opportunamente riscritta. . . int mcd(int m, int n){ if (m!=n) { if (m>n) m=m-n; else n=n-m; return mcd(m, n); } else return m; } … traslata in ciclo: int mcd(int m, int n){ while (m!=n) if (m>n) m=m-n; else n=n-m; return m; }

ESERCIZIO 1 Dati tre valori a b c che rappresentano le lunghezze di tre segmenti, valutare se posso-no essere i tre lati di un triangolo, e se sì deci-derne il tipo (scaleno, isoscele, equilatero). Vincolo: deve essere c < (a+b) Rappresentazione delle informazioni: • la variabile booleana triangolo indica se i tre segmenti possono costituire un triangolo • le variabili booleane scaleno, isoscele e equil indicano il tipo di triangolo.

ESERCIZIO 1 Specifica: se a+b>c triangolo = vero se a=b=c { equil=isoscele=vero scaleno=falso } altrimenti se a=b o b=c o a=c { isoscele=vero; equil=scaleno=falso } altrimenti { scaleno=vero; equil=isoscele=falso } altrimenti triangolo = falso

ESERCIZIO 1 main (){ float a=1. 5, b=3. 0, c=4. 0; int triangolo, scaleno, isoscele, equil; triangolo = (a+b>c); if (triangolo) { if (a==b && b==c) { equil=isoscele=1; scaleno=0; } else if (a==b || b==c || a==c) { isoscele=1; scaleno=equil=0; } else { scaleno=1; isoscele=equil=0; } } }

ESERCIZIO 1 Non si può usare l’istruzione di main (){ scelta multipla (switch) perché float a=1. 5, b=3. 0, c=4. 0; le condizioni da verificare sono int triangolo, scaleno, isoscele, equil; uguaglianze fra variabili, non triangolo = (a+b>c); semplici confronti con etichette if (triangolo) { predefinite. if (a==b && b==c) { equil=isoscele=1; scaleno=0; } else if (a==b || b==c || a==c) { isoscele=1; scaleno=equil=0; } Attenzione! Una espressione else come a==b==c sarebbe stata { scaleno=1; isoscele=equil=0; } formalmente lecita, ma avreb} be avuto tutt’altro significato! }

ESERCIZIO 2 Dati due valori positivi X e Y, calcolarne la divisione intera X/Y come sequenza di sottrazioni, ottenendo quoziente e resto. Invariante di ciclo: X = Q * Y + R, con R 0 • inizialmente, Q=0, R=X (R>Y) • a ogni passo, Q’=Q+1, R’=R-Y (R>Y) • alla fine, X = Q(n) * Y + R (n) (0<R<Y) che è la definizione di divisione intera.

ESERCIZIO 2 Specifica: sia Q il quoziente, inizialmente paridiauna 0 espressione Notare l’uso sia R il resto, inizialmente pari a X per concatenare due concatenata while (R Y) assegnamenti e inizializzare così incrementare ildue quoziente Q variabili. decrementare R di una quantità Y Idem per le operazioni Codifica di modifica main(){ int x = 20, y = 3, q, r; for (q=0, r=x; r>=y; q++, r=r-y); }

OPERATORI DI ASSEGNAMENTO “COMPATTI” Il C introduce una forma particolare di assegnamento che ingloba anche un’operazione aritmetica o bit a bit: l-espr = <espressione> è “quasi equivalente” a l-espr = l-espr <espressione> dove indica un operatore fra +, –, *, /, %, >>, <<, &, ^, |

OPERATORI DI ASSEGNAMENTO “COMPATTI” Perché “quasi” equivalente ? · nel primo caso, l-espr viene valutata una sola volta · nel secondo, invece, viene valutata due volte · Quindi, le due forme sono equivalenti solo se la valutazione di l-espr non comporta effetti collaterali

OPERATORI DI ASSEGNAMENTO “COMPATTI” Esempi k += j equivale a k = k + j k *= a + b equivale a k = k*(a+b)*/ v[i++] *= n non equivale a v[i++] = v[i++]*n */

ESERCIZIO 3 Dati tre valori a, b, c, rappresentanti i coefficienti di un’equazione di secondo grado a x 2 + b x + c = 0, calcolarne le radici (reali). Specifica: Calcolare il valore delta = b 2 - 4 ac Se delta 0 calcolare d = delta calcolare le due radici x 1, x 2 = - (b d) / 2 a altrimenti (radici complesse: halt)

ESERCIZIO 3 #include <math. h> main (){ float a=1. 0, b=2. 0, c=-15. 0; Direttiva al preprocessore: float delta, d, include x 1, x 2; la libreria matematica (fornisce la funzione sqrt) delta = b*b-4*a*c; if (delta>=0){ d = sqrt(delta); x 1 = -(b+d)/(2*a); x 2 = -(b-d)/(2*a); } }

ESERCIZIO 4 Scrivere una funzione che verifichi se un naturale N è primo. Specifica di I° livello (Crivello di Eratostene): Occorre provare a dividere N per tutti i numeri K N: se nessuno risulta essere un divisore, allora N è primo Specifica di II° livello: Se N è 1, 2 o 3, allora è primo senz’altro. Altrimenti, se è un numero pari, non è primo. Se invece N è dispari e >3, occorre tentare tutti i possibili divisori da 3 in avanti, fino a N.

ESERCIZIO 4 #include <math. h> int is. Prime(int n) { int max, i; if (n>=1 && n<=3) return true; /* 1, 2, 3 ok */ if (n%2==0) return false; /* numeri pari no */ max = sqrt(n); for(i=3; i<=max; i+=2) if (n%i==0) return false; return true;

ESERCIZIO 5 Scrivere una funzione radice che calcoli la radice quadrata (intera) di un naturale N. Specifica di I° livello: int radice(int n); restituisce il massimo intero X tale che X*X N Specifica di II° livello: Considera un naturale X dopo l’altro a partire da 1, e calcolane il quadrato X*X: fermati appena tale quadrato supera N. Il precedente numero considerato (X-1) è il risultato.

ESERCIZIO 5 int radice(int n) { int x; for(x=0; x*x <= n; x++); return x-1; } Il corpo del ciclo è vuoto: in effetti, l’elaborazione consiste solo nell’incrementare x per un opportuno numero di volte.

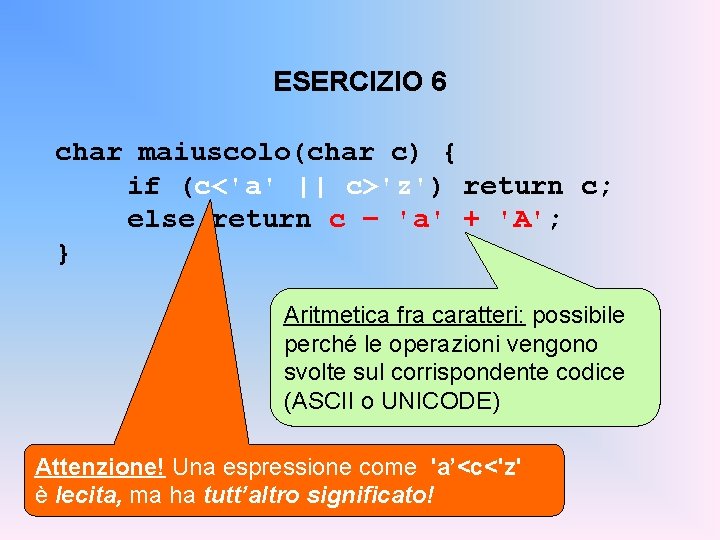
ESERCIZIO 6 Scrivere una funzione che, dato un carattere C, restituisca il corrispondente maiuscolo. Specifica di I° livello: char maiuscolo(char c); restituisce il maiuscolo di C Specifica di II° livello: Se C non è una lettera minuscola, restituiscilo tale e quale. Altrimenti, per calcolare il corrispondente maiuscolo, sfrutta l’ ordinamento della codifica dei caratteri: – ogni carattere è associato a un intero – le lettere da ‘A’ a ‘Z’ sono in sequenza – le lettere da ‘a’ a ‘z’ sono in sequenza

ESERCIZIO 6 char maiuscolo(char c) { if (c<'a' || c>'z') return c; else return c – 'a' + 'A'; } Aritmetica fra caratteri: possibile perché le operazioni vengono svolte sul corrispondente codice (ASCII o UNICODE) Attenzione! Una espressione come 'a’<c<'z' è lecita, ma ha tutt’altro significato!