Iterazione enumerativa for Il costrutto iterativo fornisce il


![Ad esempio, per azzerare le componenti di un vettore a[k] di 100 componenti, si Ad esempio, per azzerare le componenti di un vettore a[k] di 100 componenti, si](https://slidetodoc.com/presentation_image_h/8070aaa5fb4962ed6bbfaa7844385935/image-3.jpg)































- Slides: 44

Iterazione enumerativa (for). Il costrutto iterativo fornisce il modo più semplice per eseguire ripetutamente una sequenza di operazioni quando sia noto a priori il numero di ripetizioni da eseguire (iterazione enumerativa). for esamina il valore di una espressione di controllo o condizione, e se la trova diversa da zero (o “vera”) esegue una o più istruzioni, altrimenti esce dal ciclo. Dopo ogni esecuzione delle istruzioni del ciclo, ne viene eseguita una che modifica il valore dell’espressione, che viene quindi controllata di nuovo. Se ha ancora valore diverso da zero il ciclo ricomincia. Le istruzioni vengono eseguite un numero prefissato di volte, dopo di che si ha l’uscita dal ciclo. Il diagramma di flusso è indicato in figura.

![Ad esempio per azzerare le componenti di un vettore ak di 100 componenti si Ad esempio, per azzerare le componenti di un vettore a[k] di 100 componenti, si](https://slidetodoc.com/presentation_image_h/8070aaa5fb4962ed6bbfaa7844385935/image-3.jpg)
Ad esempio, per azzerare le componenti di un vettore a[k] di 100 componenti, si possono scrivere le istruzioni seguenti: for (k = 1; k <= 100; k = k + 1) a[k] = 0; dove la parentesi che segue for contiene, nell’ordine, • l’inizializzazione della variabile di controllo (k); • la condizione che, se risulta vera, determina la ripetizione del ciclo; • l’istruzione che fa variare la variabile di controllo. Inizialmente l’istruzione for imposta il contatore k a 1, e dato che questo valore rende vera (cioè diversa da zero) l’espressione di controllo (k <= 100), viene eseguita l’(unica) istruzione, che azzera il valore della componente a[1].

Quindi for incrementa di 1 il valore di k, e risultando k = 2 (e quindi ancora k <= 100), viene ripetuta l’istruzione. Viene così azzerato il valore di a[2], e così via. Dopo che è stato azzerato il valore di a[100], risulta k = 101, il che determina l’uscita dal ciclo e l’esecuzione della istruzione successiva (se presente). Il valore finale del contatore può essere: • maggiore di quello iniziale, come in questo esempio, oppure minore; in tale caso la variabile contatore va decrementata a ogni passo di iterazione; • una costante oppure una variabile (alla quale sia stato naturalmente assegnato in precedenza un valore).

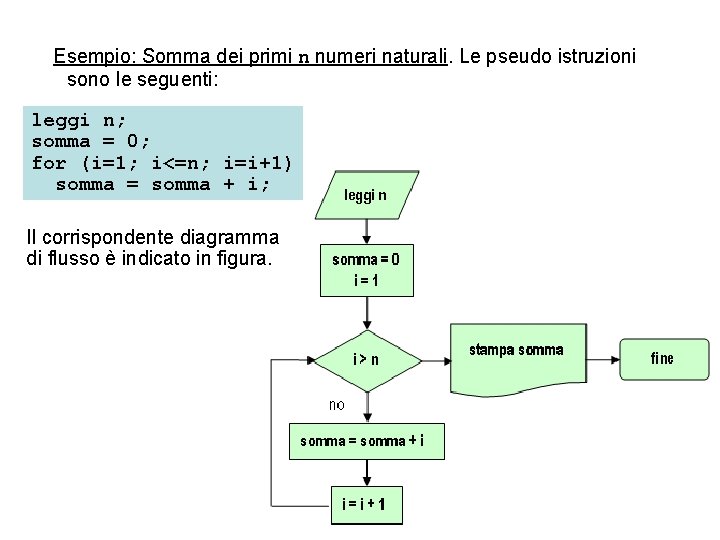
Esempio: Somma dei primi n numeri naturali. Le pseudo istruzioni sono le seguenti: leggi n; somma = 0; for (i=1; i<=n; i=i+1) somma = somma + i; Il corrispondente diagramma di flusso è indicato in figura.

Osserviamo che l’algoritmo qui impiegato non è molto efficiente, dato che la somma dei primi n numeri naturali è fornita direttamente dalla formula di Gauss n*(n+1)/2 ma l’esempio è solo indicativo del funzionamento di molti dei cicli che si incontrano in pratica.

Iterazione con guardia all’inizio (while). Nel caso invece in cui non sia noto a priori o non si voglia indicare il numero di ripetizioni da eseguire (iterazione non enumerativa), il linguaggio C mette a disposizione i due costrutti while e do-while, il primo con guardia all’inizio (come for), il secondo con guardia alla fine. Il costrutto while inizia esaminando il valore di una espressione di controllo o condizione. Se essa è diversa da zero (ossia è vera) le istruzioni del ciclo vengono eseguite, altrimenti si ha l’uscita dal ciclo. Dopo le istruzioni del ciclo ne viene eseguita una che altera il valore dell’espressione di controllo, e quando questa risulta uguale a zero si ha l’uscita del ciclo.

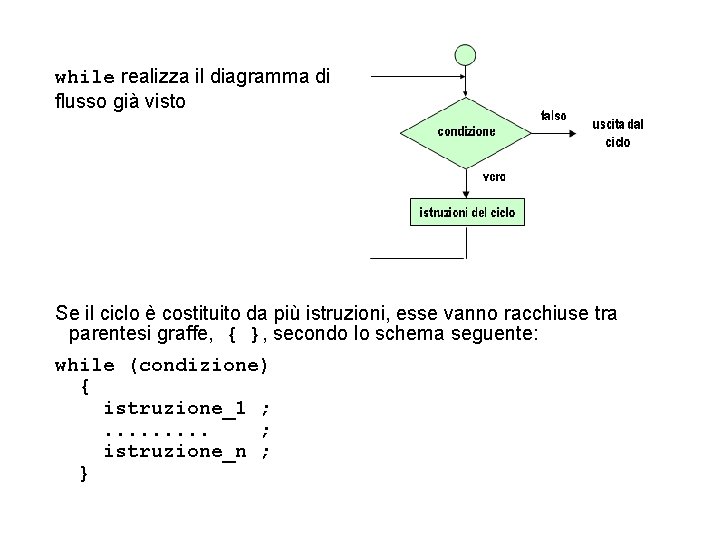
while realizza il diagramma di flusso già visto Se il ciclo è costituito da più istruzioni, esse vanno racchiuse tra parentesi graffe, { }, secondo lo schema seguente: while (condizione) { istruzione_1 ; . . ; istruzione_n ; }

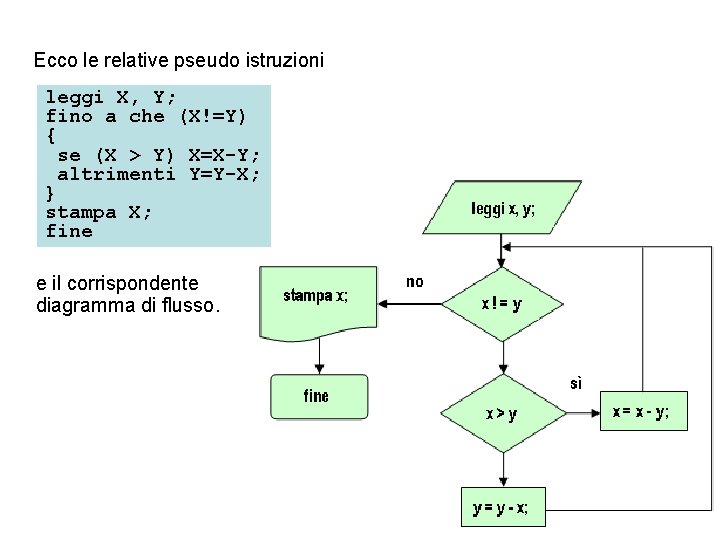
Esempio: Massimo Comun Divisore (2). Come esempio di iterazione non enumerativa con guardia all’inizio, si consideri il seguente algoritmo, derivato anch’esso dal metodo di Euclide per trovare il Massimo Comun Divisore (MCD) di due interi positivi. Per trovare il MCD di due interi positivi: • si sottrae il minore dal maggiore • se la differenza è uguale al minore, essa rappresenta il MCD cercato • altrimenti la differenza trovata sostituisce il maggiore dei due numeri, e il procedimento ricomincia da capo.

Ecco le relative pseudo istruzioni leggi X, Y; fino a che (X!=Y) { se (X > Y) X=X-Y; altrimenti Y=Y-X; } stampa X; fine e il corrispondente diagramma di flusso.

Esempio: Stampa numero massimo. Come altro esempio di iterazione non enumerativa con guardia all’inizio, si può considerare il problema di: trovare il massimo di un elenco di numeri immessi da tastiera. In questo caso non conviene usare una iterazione enumerativa perché potrebbe non essere noto a priori il numero di numeri che si immetteranno (e quindi il numero di iterazioni da eseguire). Conviene invece terminare l’elenco dei numeri con uno, detto sentinella, che sicuramente non si presenterà nell’elenco, e ogni volta che si legge un numero immesso controllare se esso sia diverso dalla sentinella. In caso affermativo il programma prosegue, in caso negativo termina. Chiamiamo: • dato la variabile nella quale sono copiati i valori di volta in volta letti • max la variabile in cui viene copiato il valore di dato se risulta dato>max e poniamo la sentinella =0.

L’espressione dell’algoritmo in pseudo istruzioni è la seguente: poni max = 0; leggi dato; while (dato!=0) { if dato > max = dato; leggi dato; } stampa max; Il diagramma di flusso è indicato in figura.

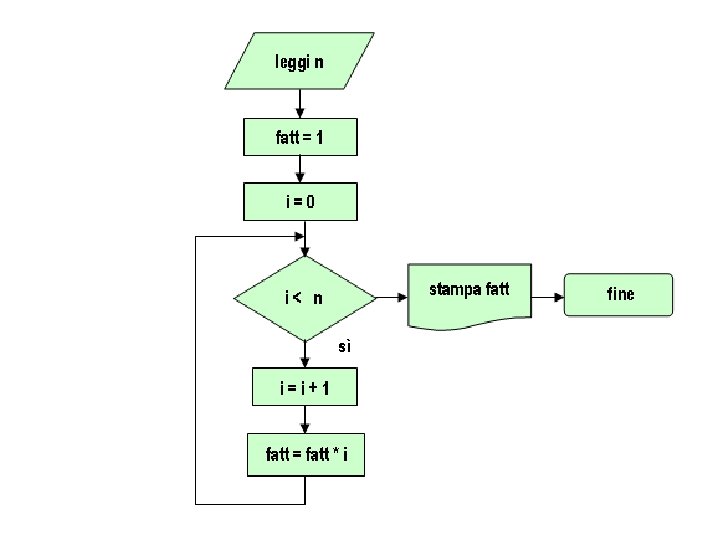
Esempio: Calcolo del fattoriale (1). Molte volte i cicli for e while sono intercambiabili. Si consideri, ad esempio, il fattoriale, n!, di un numero intero n, definito come il prodotto degli interi 1 * 2 * 3 *. . . * n (definizione iterativa). Quindi: 1! = 1 2! = 1 * 2 = 2. . . 5! = 1 * 2 * 3 * 4 * 5 = 120 Questa definizione può dare luogo (per n 1) al semplice diagramma di flusso seguente:


Esso può essere realizzato dal ciclo while seguente: fatt = 1; i = 0; while (i < n) { i = i + 1; fatt = fatt * i; } oppure dal ciclo for seguente: fatt = 1; for (i = 1; i <= n; ++i) fatt = fatt * i; Vedremo più avanti un approccio del tutto diverso per calcolare il fattoriale.

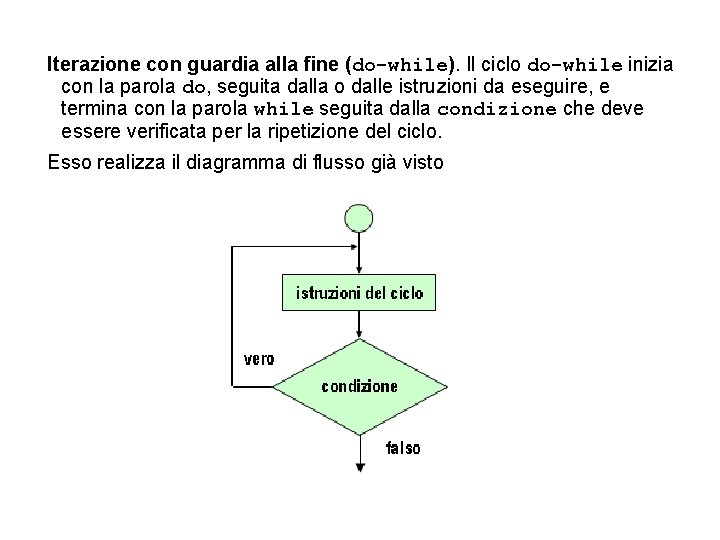
Iterazione con guardia alla fine (do-while). Il ciclo do-while inizia con la parola do, seguita dalla o dalle istruzioni da eseguire, e termina con la parola while seguita dalla condizione che deve essere verificata per la ripetizione del ciclo. Esso realizza il diagramma di flusso già visto

Esempio: moltiplicazione tramite addizioni ripetute. Come primo esempio di ciclo do-while, consideriamo le pseudo istruzioni che traducono l’algoritmo della moltiplicazione tramite addizioni ripetute. p = 0; k = a; do { p = p + b; k = k - 1; } while (k == 0); Naturalmente il costrutto do-while consente di eseguire anche un ciclo nel quale sia noto a priori il numero di ripetizioni, cioè una iterazione enumerativa. Si consideri il seguente esempio.

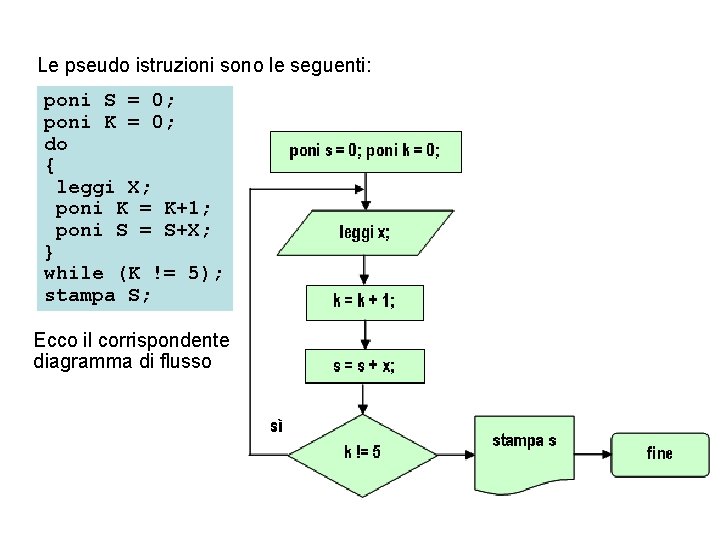
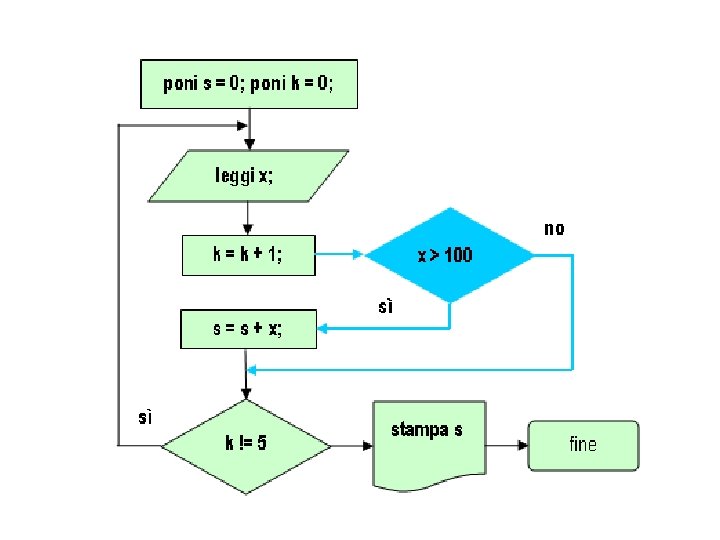
Esempio: Somma di 5 numeri. Per scrivere un algoritmo che legga 5 numeri e ne stampi la somma usiamo le seguenti variabili: • S per contenere la somma • K per contare il numero dei valori letti (ossia quante volte è stato eseguito il ciclo), • X per indicare il numero di volta in volta letto.

Le pseudo istruzioni sono le seguenti: poni S = 0; poni K = 0; do { leggi X; poni K = K+1; poni S = S+X; } while (K != 5); stampa S; Ecco il corrispondente diagramma di flusso

La traduzione di queste istruzioni in un programma C è immediata, come vedremo più avanti. Esercizio. Una leggera modifica dei questo diagramma di flusso, ponendo la guardia all’inizio, consente di risolvere il seguente problema: scrivere un algoritmo che legga 5 numeri e stampi la somma di quelli maggiori di 100 come indica la figura seguente.


Calcolo della radice quadrata. Il calcolo della radice quadrata di un numero x 0 può essere eseguito con il metodo delle approssimazioni successive. Questo consiste nel calcolare dapprima il valore di prima approssimazione, x 1, con la formula Da x 1 si calcola il valore di seconda approssimazione, x 2, con la formula Se in questa formula si sostituisce a x 1 il valore trovato di x 2, si ottiene x 3

e così di seguito. Il calcolo termina quando si è calcolato un valore che differisca dal precedente meno di un numero scelto piccolo a piacere (eps). Supponiamo, per esempio, di volere calcolare la radice quadrata di x 0 = 16. Avremmo: x 1 x 2 x 3 x 4 x 5 = = = 16/2 = 8 (16/8 + 8)/2 = 5 (16/5 + 5)/2 = 4, 1 (16/4, 1 + 4, 1)/2 = 4, 0012195121 (16/4, 0012195 + 4, 0012195)/2 = 4, 0000001858

L’algoritmo si traduce nelle seguenti pseudo istruzioni: leggi x 0, eps; x 2 = x 0/2; do { x 1 = x 2; x 2=(x 0/x 1+x 1)/2; d = x 1 - x 2; } while (d > eps) stampa x 2; e quindi nel diagramma di flusso indicato a lato

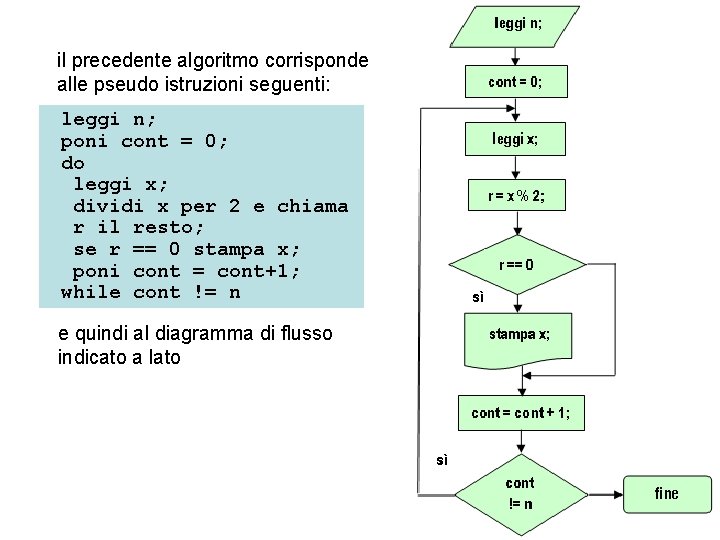
Esercizio: stampa di numeri pari. Scrivere un algoritmo che stampi i numeri pari di un elenco. L’algoritmo può essere il seguente: Si calcola il resto della divisione per 2 di ogni valore dell’elenco, e si stampano i soli valori per i quali tale resto sia 0. Si ripete l’operazione per tutti i valori dell’elenco, supponendo noto il loro numero. Se indichiamo con: - n il numero degli elementi dell’elenco - x l’elemento via letto - r il resto della divisione per 2 di ogni elemento (pertanto r = 0 se l’elemento letto è pari) - cont un contatore che memorizza il numero di elementi letti (ossia di ripetizioni del ciclo)

il precedente algoritmo corrisponde alle pseudo istruzioni seguenti: leggi n; poni cont = 0; do leggi x; dividi x per 2 e chiama r il resto; se r == 0 stampa x; poni cont = cont+1; while cont != n e quindi al diagramma di flusso indicato a lato

Cicli nidificati. Anche i cicli do-while, come gli altri, si possono trovare l’uno dentro l’altro, cioè essere nidificati. Vediamo, a questo proposito, un algoritmo che stampa la tavola pitagorica di dimensione n qualsiasi. Ovviamente esso può essere realizzato sia con un ciclo do-while, sia con uno for.


Confronto tra do-while e while. Si considerino i seguenti segmenti di programmi: cont = 10; do { printf(“%d “, cont); -- cont; } while (cont >= 5); cont = 10; while (cont >= 5) { printf(“%d “, cont); -- cont; } Sebbene producano entrambi la stampa dei numeri 10, 9, 8, 7, 6, 5, dal punto di vista concettuale essi non sono equivalenti.

Infatti nel ciclo do-while, nel quale la guardia è alla fine, le istruzioni contenute all’interno sono eseguite almeno una volta, mentre nel ciclo while, nel quale la guardia è all’inizio, le istruzioni potrebbero anche non essere eseguite mai. Pertanto lo schema do-while non consente di rappresentare facilmente tutti i casi di iterazione che si possono incontrare in pratica, e quindi la scelta tra i due tipi di cicli va effettuata con attenzione. Mostriamo ciò con il seguente esempio.

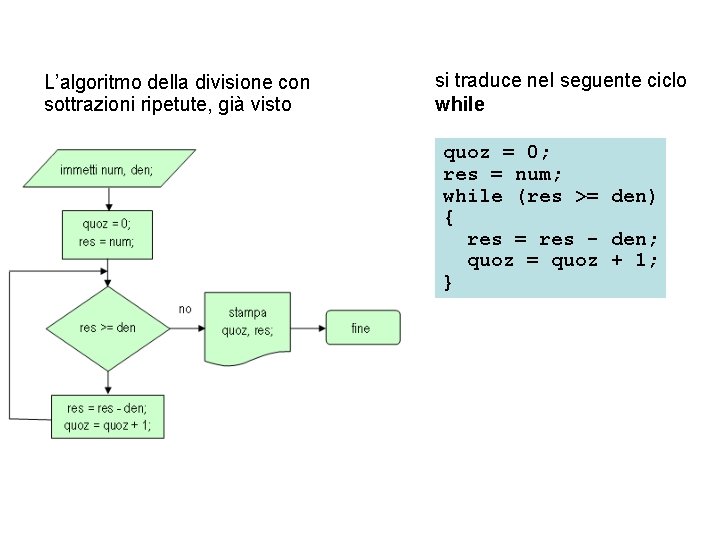
L’algoritmo della divisione con sottrazioni ripetute, già visto si traduce nel seguente ciclo while quoz = 0; res = num; while (res >= den) { res = res - den; quoz = quoz + 1; }

In questo algoritmo lo schema while esprime la ripetizione di una sequenza di due azioni, controllata dalla condizione res >= den, che specifica la condizione per rimanere dentro l’iterazione. La condizione viene valutata prima di ogni esecuzione della sequenza e, se è falsa, la ripetizione termina (o non ha inizio, se si è all’inizio del processo). Viceversa, se utilizzassimo il seguente ciclo do-while quoz = 0; res = num; do { res = res - den; quoz = quoz + 1; } while (res < den);

scriveremmo una sequenza non corretta, in quanto fornisce un risultato errato se il dividendo è minore del divisore. Ad esempio, se (num == 15) e (den == 20), otterremmo quoz = 1 e res = – 5 (al posto dei valori corretti quoz = 0 e res = 20). Affinché la sequenza sia corretta occorre che le istruzioni del ciclo non siano eseguite quando la condizione di ripetizione (res < den) si verifica prima dell’inizio dell’iterazione. Osserviamo che ciascuna delle tre strutture, sequenza, selezione, iterazione, presenta un unico punto di entrata e un unico punto di uscita. Ciò comporta che esse siano “componibili” sequenzialmente, ovvero che si possano collegare in successione. Esse si possono anche nidificare l’una dentro l’altra, senza alcun limite.

Iterazione e ricorsività La potenza dei calcolatori è dovuta alla loro capacità di eseguire in modo ripetitivo lo stesso compito o versioni diverse di esso. Nell’informatica il concetto di iterazione s’incontra in molte forme, tra le quali i modelli dei dati dove molti concetti, come le liste, sono definiti in modo ripetitivo. Per esempio: una lista è vuota oppure è un elemento seguito da un altro, seguito da un altro ancora e così via. Alternativa all’iterazione è la ricorsività, una tecnica in cui un concetto viene definito, direttamente o indirettamente, in termini di se stesso. Per esempio una lista si può definire anche come: una lista è vuota oppure è un elemento seguito da una lista


La ricorsività è prevista in molti linguaggi di programmazione tra i quali il C, che consente di definire funzioni ricorsive, che possono cioè invocare se stesse sia direttamente, all’interno del proprio corpo, sia indirettamente, invocando un’altra funzione che ne invoca un’altra, che a sua volta ne invoca un’altra ancora a così via, finché qualche funzione in questa sequenza invoca quella di partenza. Spesso i programmatori alle prime armi si sentono più sicuri quando scrivono programmi iterativi piuttosto che programmi ricorsivi, ma è buona abitudine abituarsi a pensare e programmare in modo ricorsivo quando ciò risulti appropriato. I programmi ricorsivi possono risultare più semplici da scrivere, analizzare e comprendere.

La ricorsività trova il suo equivalente nel procedimento matematico della induzione, utilizzato per dimostrare la verità di un asserto. In una dimostrazione induttiva si dimostra che un asserto S(n), funzione di una variabile n è vero, dimostrando dapprima una base, ovvero l’asserto S(n) per un valore particolare di n. Per esempio si pone n = 0 e si dimostra l’asserto S(0). Successivamente si prova un passo induttivo, nel quale si dimostra che l’asserto S, per un generico valore del suo argomento, deriva dalla verità dell’asserto medesimo per valori precedenti del suo argomento. Nella forma più semplice di induzione, si dimostra che S(n) implica S(n+1)qualunque sia n 0.

Per esempio, S(n) potrebbe essere l’asserto: la somma degli interi da 1 a n è uguale a n*(n+1)/2 cioè S(n) potrebbe essere la nota formula = n*(n+1)/2 La base sarebbe allora S(1), ovvero l’equazione precedente con 1 al posto di n, che si riduce semplicemente all’uguaglianza 1 = 1 * 2/2. Il passo induttivo consiste nel dimostrare che, supposta vera S(n) (cioè la formula precedente), risulta vera anche S(n+1), cioè l’equazione = (n+1)*(n+2)/2

Ora, che questa equazione sia vera è evidente, in quanto la formula = n*(n+1)/2 è valida per qualsiasi valore di n, quindi anche per n+1, valore che sostituito in essa fornisce appunto l’equazione = (n+1)*(n+2)/2 L’iterazione e la ricorsività sono due concetti fondamentali che compaiono in varie forme nei modelli dei dati, nelle strutture dati e negli algoritmi. Vediamo alcuni esempi di utilizzo del secondo concetto, riscrivendo in modo ricorsivo la definizione di fattoriale, già vista nella sua versione iterativa.

Definizione ricorsiva di fattoriale. La funzione fattoriale si può definire in maniera ricorsiva come segue: base: 1! = 1 induzione: n! = n * (n – 1)! Dato che la base ci dice che 1! = 1, possiamo utilizzare questo fatto nel passo induttivo con n = 2 per determinare 2!, scrivendo: 2! = 2 * 1 = 2. Con n = 3, 4 e 5 otteniamo: 3! = 3 * 2 = 6 4! = 4 * 3! = 4 * 6 = 24 5! = 5 * 4! = 5 * 24 = 120 e così via.

Notiamo che, sebbene possa sembrare che il termine “fattoriale” sia definito in termini di se stesso, in pratica possiamo ottenere il valore di n!, per valori via maggiori di n, nei termini del fattoriale di valori più piccoli di n. Abbiamo dunque una definizione “sensata” di fattoriale. La trascrizione di questa definizione ricorsiva di n! è costituita dal frammento di programma seguente: if (n == 0) return(1); return(n * fatt(n - 1));

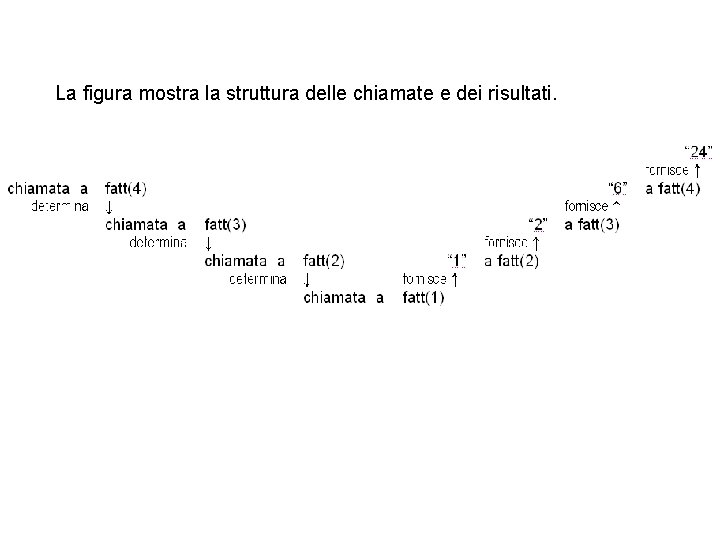
Per esempio, se effettuiamo la chiamata fatt(4), il risultato è una chiamata a fatt(3), che chiama fatt(2), che a sua volta chiama fatt(1). A questo punto, fatt(1) applica la regola base, poiché n<=1, e restituisce il valore 1 a fatt(2). La chiamata fatt(2) termina l’esecuzione della penultima linea, restituendo 2 a fatt(3). A sua volta, fatt(3) restituisce 6 a fatt(4), che completa l’esecuzione della linea restituendo 24 come risposta.

La figura mostra la struttura delle chiamate e dei risultati.

Definizione ricorsiva di potenza. Anche la potenza può essere definita in modo ricorsivo. Consideriamo la funzione pot, che ha come argomenti • un numero reale positivo, base, elevato a • un numero intero, esp. Risulta che pot(base, esp) può essere definita in maniera ricorsiva come segue: base: pot(base, 0) = 1 induzione: pot(base, esp) = base * pot(base, esp-1). Ciò dà luogo al seguente segmento di programma, che calcola la potenza in modo ricorsivo: if (esp == 0) pot(base, esp) = 1 else pot(base, esp) = base*pot(base, esp-1)
 Iterazione enumerativa
Iterazione enumerativa Algoritmo finito
Algoritmo finito Iterazione enumerativa
Iterazione enumerativa Costo primo
Costo primo Costrutto di competenza
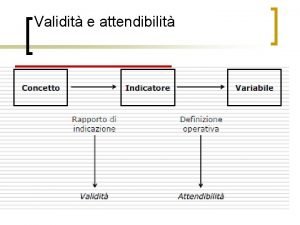
Costrutto di competenza Validità di costrutto
Validità di costrutto Validità di costrutto
Validità di costrutto Validità di costrutto
Validità di costrutto Metodo split half
Metodo split half Tres bellas que bellas son autor
Tres bellas que bellas son autor La coma en la aclaración
La coma en la aclaración Iterazione precondizionale
Iterazione precondizionale Incremental e iterativo
Incremental e iterativo Iterativo
Iterativo Planejamento iterativo
Planejamento iterativo Iterativo
Iterativo Busca de aprofundamento iterativo
Busca de aprofundamento iterativo Strutture iterative
Strutture iterative Servidor concurrente
Servidor concurrente Fibonacci iterativo
Fibonacci iterativo Exspektans eller expektans
Exspektans eller expektans Bo bergman jag fryser om dina händer
Bo bergman jag fryser om dina händer Stig kerman
Stig kerman Strategi för svensk viltförvaltning
Strategi för svensk viltförvaltning Anatomi organ reproduksi
Anatomi organ reproduksi Informationskartläggning
Informationskartläggning Typiska drag för en novell
Typiska drag för en novell Standardavvikelse formel
Standardavvikelse formel Tack för att ni har lyssnat
Tack för att ni har lyssnat Läkarutlåtande för livränta
Läkarutlåtande för livränta Klassificeringsstruktur för kommunala verksamheter
Klassificeringsstruktur för kommunala verksamheter Centrum för kunskap och säkerhet
Centrum för kunskap och säkerhet Inköpsprocessen steg för steg
Inköpsprocessen steg för steg Påbyggnader för flakfordon
Påbyggnader för flakfordon Tack för att ni lyssnade
Tack för att ni lyssnade En lathund för arbete med kontinuitetshantering
En lathund för arbete med kontinuitetshantering Egg för emanuel
Egg för emanuel Tack för att ni har lyssnat
Tack för att ni har lyssnat Rutin för avvikelsehantering
Rutin för avvikelsehantering Var finns arvsanlagen
Var finns arvsanlagen Presentera för publik crossboss
Presentera för publik crossboss Myndigheten för delaktighet
Myndigheten för delaktighet Debattartikel struktur
Debattartikel struktur Var 1721 för stormaktssverige
Var 1721 för stormaktssverige Densitet vatten
Densitet vatten