Massimi minimi e flessi lo studio di funzione

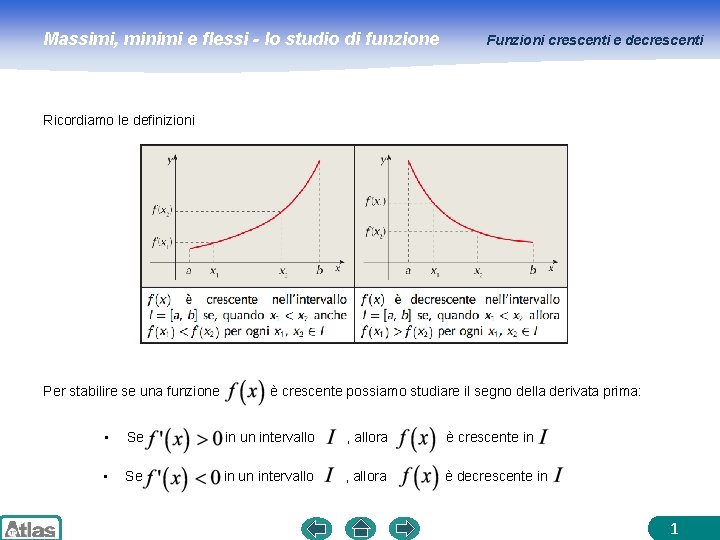
Massimi, minimi e flessi - lo studio di funzione Funzioni crescenti e decrescenti Ricordiamo le definizioni Per stabilire se una funzione è crescente possiamo studiare il segno della derivata prima: • Se in un intervallo , allora è crescente in • Se in un intervallo , allora è decrescente in 1

Massimi, minimi e flessi - lo studio di funzione Funzioni crescenti e decrescenti ESEMPIO Data la funzione di equazione determiniamo gli intervalli in cui essa è crescente e quelli in cui è decrescente. La funzione ha dominio Calcoliamone la derivata prima e studiamone il segno: 3 -1 La funzione è quindi: • crescente se • decrescente se + nte fc ce res fd − + ec res c en te f te en sc cre 2

Massimi, minimi e flessi - lo studio di funzione Massimi e minimi di una funzione Massimi e minimi assoluti Considerata una funzione • massimo assoluto di • minimo assoluto di definita in un intervallo I, chiamiamo: in I il valore M, se esiste, per il quale in I il valore m, se esiste, per il quale 3

Massimi, minimi e flessi - lo studio di funzione Massimi e minimi di una funzione Massimi e minimi relativi Sia f (x) una funzione definita in un intervallo [a, b], e sia x 0 un punto di tale intervallo: • il punto x è un punto di massimo relativo se esiste un intorno I (x 0) per tutti i punti x del quale si ha che In tal caso f (x 0) rappresenta il massimo relativo della funzione. • il punto x 0 è un punto di minimo relativo se esiste un intorno I (x 0) per tutti i punti x del quale si ha che In tal caso f (x 0) rappresenta il massimo relativo della funzione. I punti di massimo e di minimo relativo, che vengono anche detti punti estremanti, sono punti di massimo e di minimo a livello locale. La funzione a lato possiede due massimi relativi e un minimo relativo. Non ha minimo assoluto, ha massimo assoluto in corrispondenza del punto M 2. 4

Massimi, minimi e flessi - lo studio di funzione La ricerca dei punti estremanti Se una funzione è derivabile, i suoi punti di massimo e di minimo vanno ricercati tra i punti che annullano la derivata prima (punti stazionari). Si verifica che: • se f’ (x) = 0 e f’ (x) è crescente in un intorno sinistro di x 0 (f’(x) > 0) e decrescente in un intorno destro (f’(x) < 0), allora x 0 è un punto di massimo. • se f’ (x 0) = 0 e f’ (x) è decrescente in un intorno sinistro di x 0 (f’(x) < 0) e crescente in un intorno destro (f’(x) < 0), allora x 0 è un punto di minimo. x 0 + x 0 − x 0 punto di massimo − + x 0 punto di minimo 5

Massimi, minimi e flessi - lo studio di funzione La ricerca dei punti estremanti ESEMPIO di dominio Sia è continua e derivabile in D • Calcoliamo la derivata prima 3 2 • Ricerchiamo i punti stazionari • Studiamo il segno di − + M + m Dalla tabella deduciamo che il punto x = 2 è di massimo relativo e il massimo vale e che il punto x = 3 è di minimo relativo e il minimo vale 6

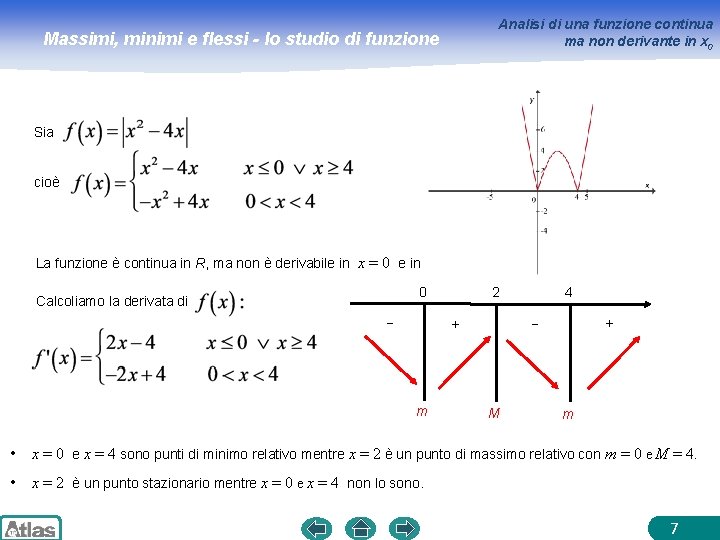
Analisi di una funzione continua ma non derivante in x 0 Massimi, minimi e flessi - lo studio di funzione Sia cioè La funzione è continua in R, ma non è derivabile in x = 0 e in x = 4: 0 Calcoliamo la derivata di − 2 + m 4 + − M m • x = 0 e x = 4 sono punti di minimo relativo mentre x = 2 è un punto di massimo relativo con m = 0 e M = 4. • x = 2 è un punto stazionario mentre x = 0 e x = 4 non lo sono. 7

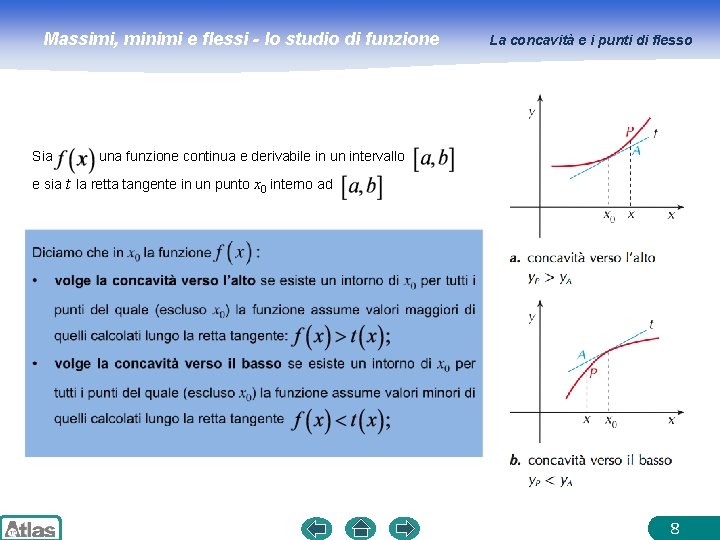
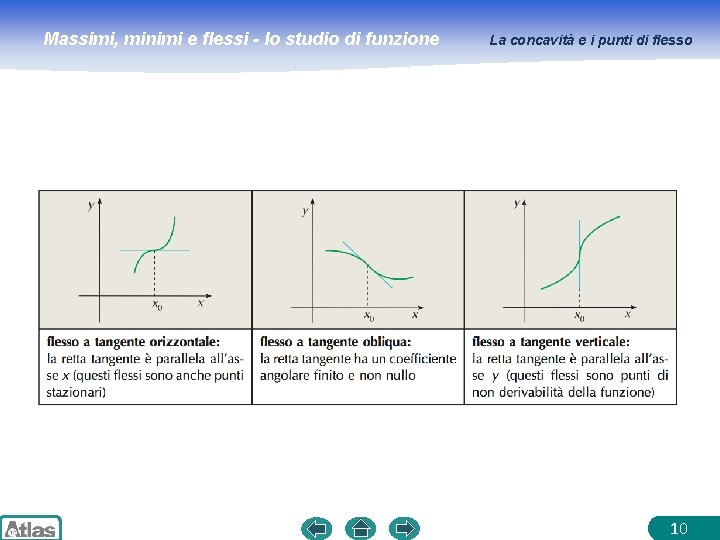
Massimi, minimi e flessi - lo studio di funzione Sia e sia La concavità e i punti di flesso una funzione continua e derivabile in un intervallo t la retta tangente in un punto x 0 interno ad 8

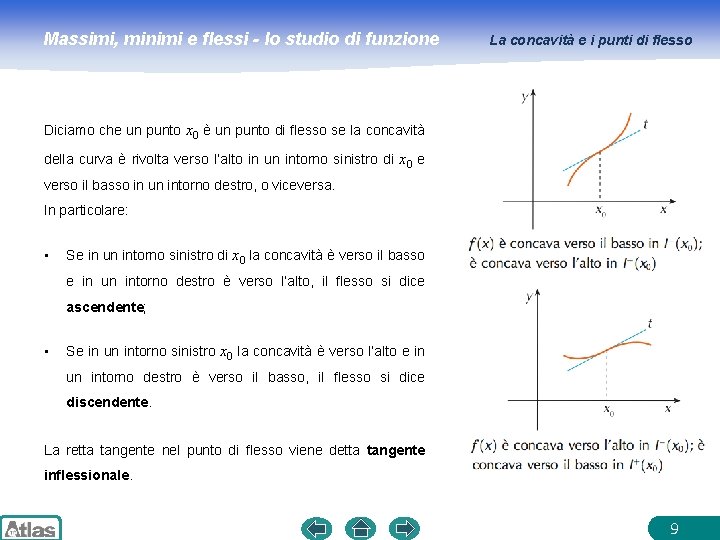
Massimi, minimi e flessi - lo studio di funzione La concavità e i punti di flesso Diciamo che un punto x 0 è un punto di flesso se la concavità della curva è rivolta verso l’alto in un intorno sinistro di x 0 e verso il basso in un intorno destro, o viceversa. In particolare: • Se in un intorno sinistro di x 0 la concavità è verso il basso e in un intorno destro è verso l’alto, il flesso si dice ascendente; • Se in un intorno sinistro x 0 la concavità è verso l’alto e in un intorno destro è verso il basso, il flesso si dice discendente. La retta tangente nel punto di flesso viene detta tangente inflessionale. 9

Massimi, minimi e flessi - lo studio di funzione La concavità e i punti di flesso 10

Massimi, minimi e flessi - lo studio di funzione Individuazione della concavità e dei punti di flesso Questi due teoremi ci permettono di studiare la concavità di una funzione e di individuare i punti di flesso. 11

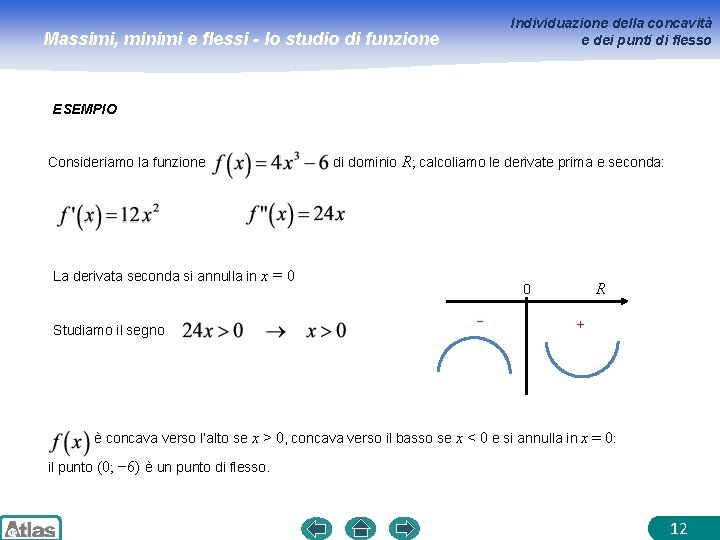
Individuazione della concavità e dei punti di flesso Massimi, minimi e flessi - lo studio di funzione ESEMPIO Consideriamo la funzione di dominio R; calcoliamo le derivate prima e seconda: La derivata seconda si annulla in x = 0 Studiamo il segno R 0 − + è concava verso l’alto se x > 0, concava verso il basso se x < 0 e si annulla in x = 0: il punto (0; − 6) è un punto di flesso. 12

Massimi, minimi e flessi - lo studio di funzione Teorema. Sia una funzione definita in un intervallo La determinazione dei punti estremanti e dei punti di flesso con le derivate successive derivabile n volte al suo interno con derivata continua. Siano poi nulle in un punto x 0 tutte le derivate a partire dalla prima fino a quella di ordine n − 1: Allora: • se n è pari (derivata di ordine pari): • se n è dispari (derivata di ordine dispari): Questo teorema è utile per determinare quali tra i punti stazionari sono estremanti oppure punti di flesso a tangente orizzontale. 13

Massimi, minimi e flessi - lo studio di funzione La determinazione dei punti estremanti e dei punti di flesso con le derivate successive ESEMPIO Studiamo la natura dei punti stazionari della funzione di dominio R. e si ha che Calcoliamo le derivate successive in tali punti fino a che ne troviamo una che non si annulla. ed è: 14

Massimi, minimi e flessi - lo studio di funzione Teorema. Sia una funzione definita in un intervallo La determinazione dei punti estremanti e dei punti di flesso con le derivate successive derivabile n volte al suo interno con derivata continua. Sia x 0 un punto per il quale si annulla la derivata seconda e quelle ad essa successive fino a quella di ordine n − 1: Sia la prima derivata che non si annulla in x 0: Allora: • se n è dispari (derivata di ordine dispari): • se n è pari (derivata di ordine pari) la funzione non ha flesso in x 0 ed ha: Con questo teorema possiamo individuare, se esistono, i punti di flesso di una funzione. 15

Massimi, minimi e flessi - lo studio di funzione La determinazione dei punti estremanti e dei punti di flesso con le derivate successive ESEMPIO Troviamo, se esistono, i punti di flesso della funzione di dominio R. Calcoliamo la derivata seconda Troviamo i punti in cui • si annulla: Calcoliamo le derivate successive in questi punti fino a che ne troviamo una che non si annulla. ed è: • Calcoliamo le derivate successive in zero. 16

Massimi, minimi e flessi - lo studio di funzione Lo studio completo di una funzione Punti da affrontare per studiare in modo completo una funzione e tracciarne il grafico: 1. determinare il dominio 2. individuare eventuali simmetrie o periodicità 3. trovare, se esistono, le intersezioni con gli assi e studiare il segno della funzione 4. studiare il comportamento agli estremi del dominio e determinare gli eventuali asintoti 5. calcolare la derivata prima e trovare i punti estremanti (massimi o minimi) 6. calcolare la derivata seconda e trovare gli eventuali punti di flesso 17

Massimi, minimi e flessi - lo studio di funzione Lo studio completo di una funzione ESEMPIO Studiamo la funzione 1. Determiniamo il dominio 2. La funzione è simmetrica rispetto all’origine; è sufficiente studiarla per x > 0. 3. Poiché 0 non appartiene al dominio, la funzione non interseca l’asse y; la funzione interseca l’asse x in x = -1 e x = 1. -1 Segno della funzione + − − 0 − − + 1 − + − -1 1 + + + 18

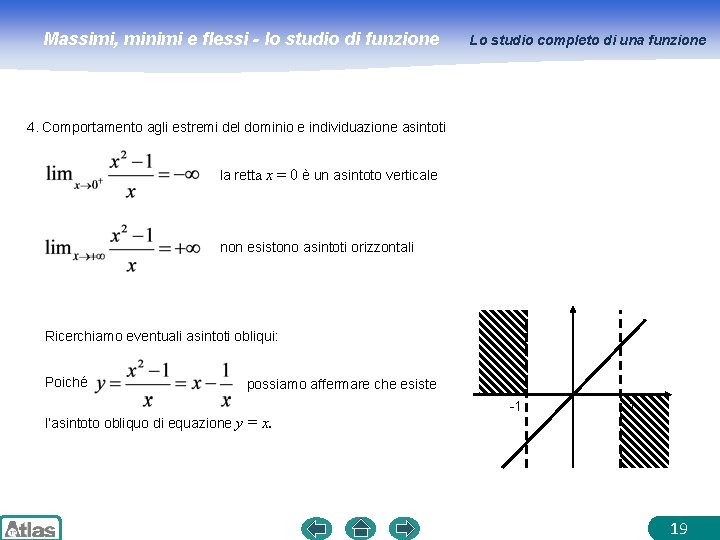
Massimi, minimi e flessi - lo studio di funzione Lo studio completo di una funzione 4. Comportamento agli estremi del dominio e individuazione asintoti la retta x = 0 è un asintoto verticale non esistono asintoti orizzontali Ricerchiamo eventuali asintoti obliqui: Poiché possiamo affermare che esiste l’asintoto obliquo di equazione y = x. -1 1 19

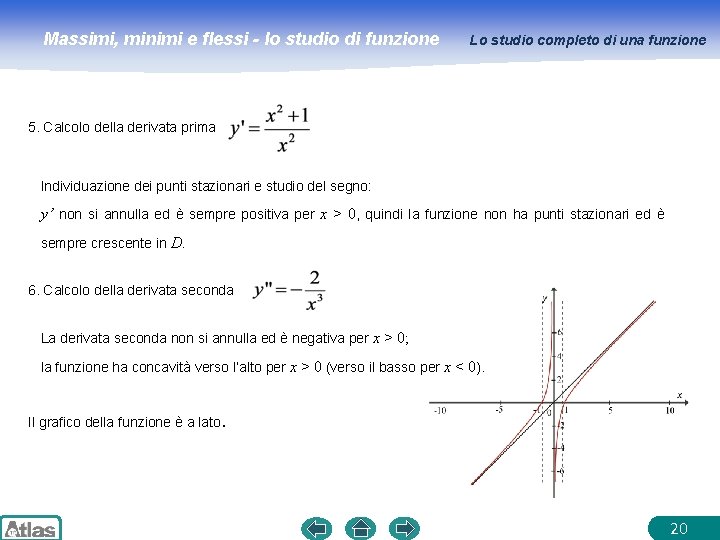
Massimi, minimi e flessi - lo studio di funzione Lo studio completo di una funzione 5. Calcolo della derivata prima Individuazione dei punti stazionari e studio del segno: y’ non si annulla ed è sempre positiva per x > 0, quindi la funzione non ha punti stazionari ed è sempre crescente in D. 6. Calcolo della derivata seconda La derivata seconda non si annulla ed è negativa per x > 0; la funzione ha concavità verso l’alto per x > 0 (verso il basso per x < 0). Il grafico della funzione è a lato. 20

Massimi, minimi e flessi - lo studio di funzione La risoluzione approssimata delle equazioni Esistenza e unicità delle soluzioni in un intervallo Ogni equazione, dopo averne determinato il dominio e svolto opportunamente i calcoli, può essere scritta nella forma dove è una funzione reale della variabile x. Le sue soluzioni possono essere determinate graficamente costruendo il diagramma di f (x) ed individuando le ascisse dei suoi punti di intersezione con l’asse x. 21

Massimi, minimi e flessi - lo studio di funzione Ricordiamo che una funzione continua La risoluzione approssimata delle equazioni ammette almeno uno zero nell’intervallo se Lo zero è unico se: • non si annulla mai in • è sempre positiva oppure sempre negativa in , oppure Quando si riesce ad individuare un intervallo dell’equazione che contiene una sola soluzione si dice che si sono separate le radici. 22

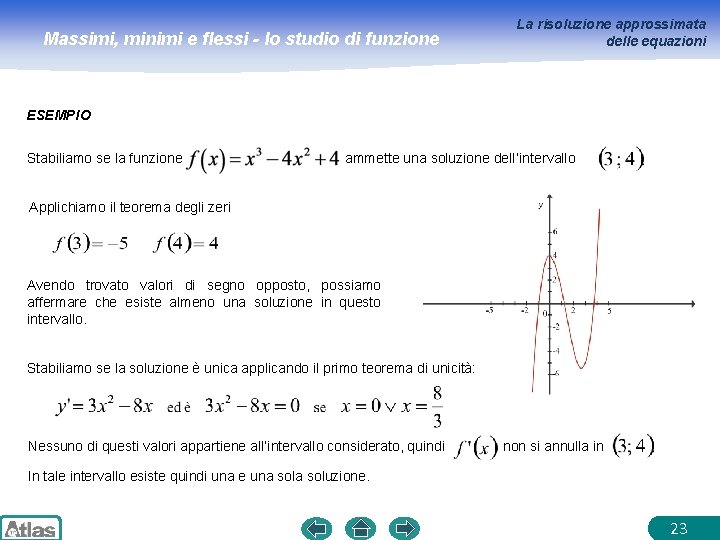
Massimi, minimi e flessi - lo studio di funzione La risoluzione approssimata delle equazioni ESEMPIO Stabiliamo se la funzione ammette una soluzione dell’intervallo Applichiamo il teorema degli zeri Avendo trovato valori di segno opposto, possiamo affermare che esiste almeno una soluzione in questo intervallo. Stabiliamo se la soluzione è unica applicando il primo teorema di unicità: Nessuno di questi valori appartiene all’intervallo considerato, quindi non si annulla in In tale intervallo esiste quindi una e una soluzione. 23

Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni Il metodo di bisezione Il metodo più semplice di individuazione delle radici è quello di bisezione; esso consiste nel dimezzare ad ogni passaggio l’intervallo che contiene la radice, fino a trovarne uno di ampiezza molto piccola. 24

Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni ESEMPIO Riprendiamo l’equazione della quale sappiamo che ammette una soluzione nell’intervallo Dimezziamo l’intervallo, e per fare ciò calcoliamo il suo punto medio: Applichiamo il teorema degli zeri: La radice appartiene all’intervallo Dimezziamo di nuovo l’intervallo valutando il punto medio: Applichiamo il teorema degli zeri: La radice appartiene all’intervallo Proseguendo in questo modo si può ridurre l’intervallo alla precisione desiderata. Nel nostro caso, dopo qualche passaggio troviamo che un valore approssimato della soluzione è 3, 70. 25

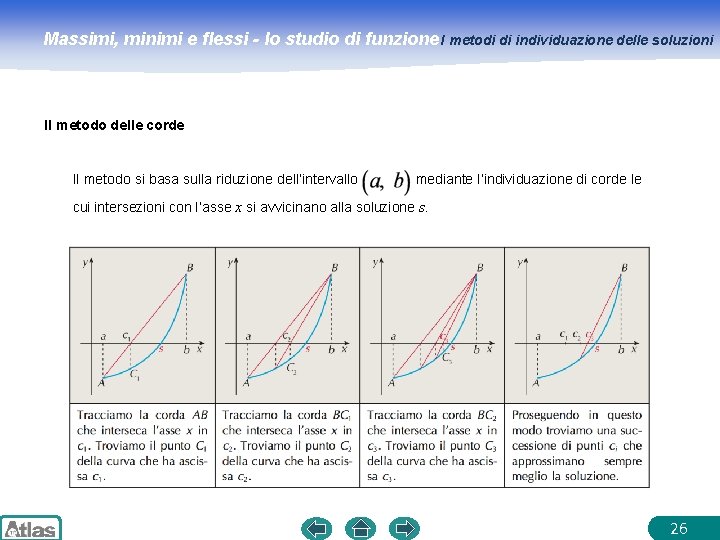
Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni Il metodo delle corde Il metodo si basa sulla riduzione dell’intervallo mediante l’individuazione di corde le cui intersezioni con l’asse x si avvicinano alla soluzione s. 26

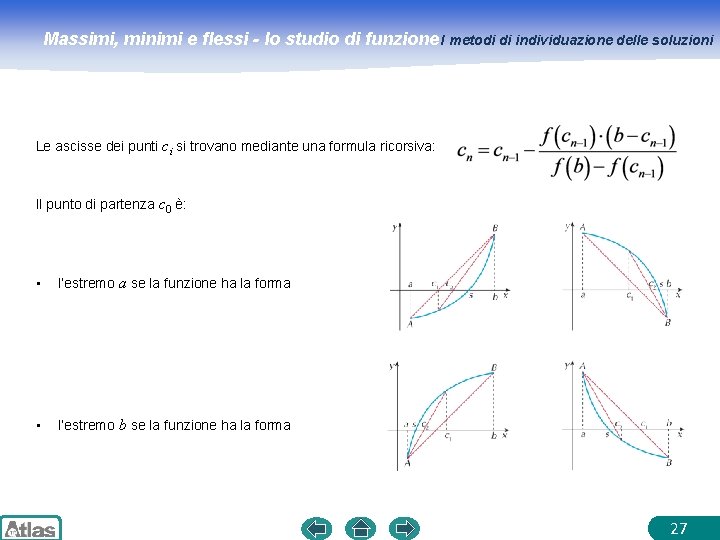
Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni Le ascisse dei punti ci si trovano mediante una formula ricorsiva: Il punto di partenza c 0 è: • l’estremo a se la funzione ha la forma • l’estremo b se la funzione ha la forma 27

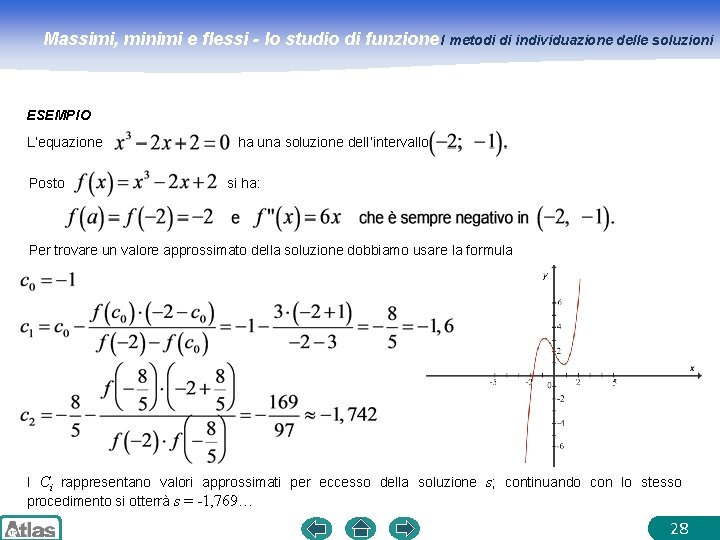
Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni ESEMPIO L’equazione Posto ha una soluzione dell’intervallo si ha: Per trovare un valore approssimato della soluzione dobbiamo usare la formula I Ci rappresentano valori approssimati per eccesso della soluzione s; continuando con lo stesso procedimento si otterrà s = -1, 769… 28

Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni Il metodo delle tangenti (metodo di Newton) Il metodo di Newton è analogo a quello precedente, ma le corde vengono sostituite dalle rette tangenti in A oppure in B. La formula ricorsiva che genera i valori approssimati è: Il punto di partenza d 0 è: • l’estremo a se hanno lo stesso segno • l’estremo b se hanno segni opposti 29

Massimi, minimi e flessi - lo studio di funzione I metodi di individuazione delle soluzioni ESEMPIO Riprendendo l’esempio precedente e applichiamo il metodo delle tangenti. Calcoliamo la derivata prima della funzione: I valori d 1, d 2, … dn rappresentano valori approssimati per difetto della soluzione s. 30