QuineMc Cluskey Method 1 Motivation Karnaugh maps are

Motivation Karnaugh maps are very effective for the minimization of expressions with up to

Quine-Mc. Cluskey Willard van Orman Quine 1908 -2000, Edgar Pierce Chair of Philosophy at

Outline of the Quine-Mc. Cluskey Method 1. Produce a minterm expansion (standard sum-of-products form)

Determination of Prime Implicants AB’CD’ + AB’CD = AB’C (The dash indicates a missing

Quine-Mc. Cluskey Method An Example 1. Find all the prime implicants group 0 0

Quine-Mc. Cluskey Method An Example Column I Combining group 0 and group 1: Column

Quine-Mc. Cluskey Method An Example Column I Does it make group 0 sense to

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1

Quine-Mc. Cluskey Method An Example Column I Again, there is no need to try

Quine-Mc. Cluskey Method An Example Column I We have now completed the first step.

Quine-Mc. Cluskey Method An Example Column I group 0 0 0000 group 1 1

Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a

Quine-Mc. Cluskey Method An Example What are the extra terms in the solution obtained

The Prime Implicant Chart The prime implicant chart is the second part of the

Prime Implicant Chart (Example) Prime Implicants minterms Question: Given the prime implicant chart above,

Prime Implicant Chart (Example) Prime Implicants minterms Similar to the Karnaugh map, all we

Prime Implicant Chart (Example) Prime Implicants minterms Once a term is included in the

Prime Implicant Chart (Example) Prime Implicants minterms 82

Prime Implicant Chart (Example) Prime Implicants minterms As we have not covered all the

Prime Implicant Chart (Example) Prime Implicants minterms What strategy should we use to find

Prime Implicant Chart (Example) Prime Implicants minterms We choose first prime implicants that cover

Prime Implicant Chart (Example) Prime Implicants minterms Therefore our minimum solution is: f(a, b,

Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7)

Cyclic Prime Implicant Chart F(a, b, c) = a’b’ + bc’ + ac F(a,

Petrick’s Method S. R. Petrick. A direct determination of the irredundant forms of a

Petrick’s Method An Example Prime Implicants minterms Step 1: Label all the rows in

Petrick’s Method An Example Prime Implicants minterms The first column has an X in

Petrick’s Method An Example Prime Implicants minterms Following this technique, we obtain: P =

Petrick’s Method An Example P = (P 1 + P 2) (P 1 +

Petrick’s Method An Example P = P 1 P 4 P 5 + P

Slides: 102

Download presentation

Quine-Mc. Cluskey Method 1

Motivation Karnaugh maps are very effective for the minimization of expressions with up to 5 or 6 inputs. However they are difficult to use and error prone for circuits with many inputs. Karnaugh maps depend on our ability to visually identify prime implicants and select a set of prime implicants that cover all minterms. They do not provide a direct algorithm to be implemented in a computer. For larger systems, we need a programmable method!! 2

Quine-Mc. Cluskey Willard van Orman Quine 1908 -2000, Edgar Pierce Chair of Philosophy at Harvard University. http: //members. aol. com/drquine/wv-quine. html Quine, Willard, “The problem of simplifying truth functions. ” American Mathematical Monthly, vol. 59, 1952. Quine, Willard, “A way to simplify truth functions. ” American Mathematical Monthly, vol. 62, 1955. Edward J. Mc. Cluskey, Professor of Electrical Engineering and Computer Science at Stanford http: //www-crc. stanford. edu/users/ejm/Mc. Cluskey_Edward. html Mc. Cluskey Jr. , Edward J. “Minimization of Boolean Functions. ” Bell Systems Technical Journal, vol. 35, pp. 1417 -1444, 1956 3

Outline of the Quine-Mc. Cluskey Method 1. Produce a minterm expansion (standard sum-of-products form) for a function F 2. Eliminate as many literals as possible by systematically applying XY + XY’ = X. 3. Use a prime implicant chart to select a minimum set of prime implicants that when ORed together produce F, and that contains a minimum number of literals. 4

Determination of Prime Implicants AB’CD’ + AB’CD = AB’C (The dash indicates a missing variable) 1010 +1011=101 - We can combine the minterms above because they differ by a single bit. The minterms below won’t combine A’BC’D + A’BCD’ 0101 +0110 5

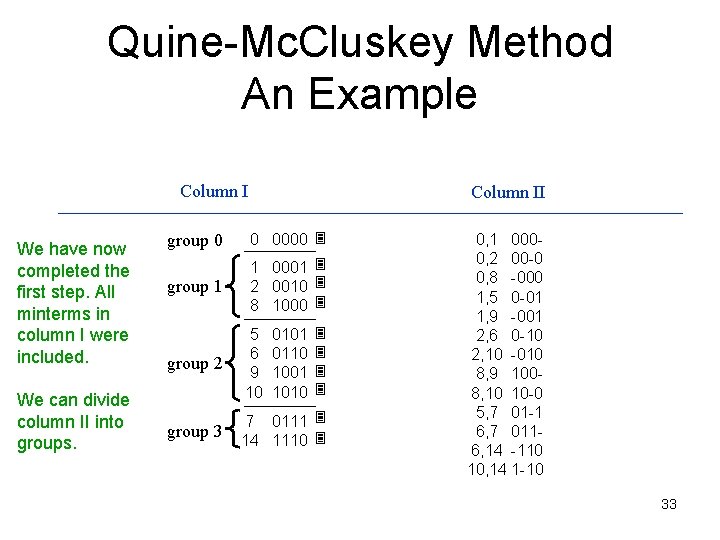
Quine-Mc. Cluskey Method An Example 1. Find all the prime implicants group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 Group the minterms according to the number of 1 s in the minterm. This way we only have to compare minterms from adjacent groups. 6

Quine-Mc. Cluskey Method An Example Column I Combining group 0 and group 1: Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 7

Quine-Mc. Cluskey Method An Example Column I Combining group 0 and group 1: Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0, 1 000 - 0101 0110 1001 1010 8

Quine-Mc. Cluskey Method An Example Column I Combining group 0 and group 1: Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0, 1 0000, 2 00 -0 0101 0110 1001 1010 9

Quine-Mc. Cluskey Method An Example Column I Does it make group 0 sense to no combine group 0 group 1 with group 2 or 3? No, there at least two bits that are different. Column II 0 0000 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 0101 0110 1001 1010 10

Quine-Mc. Cluskey Method An Example Column I Does it make group 0 sense to no combine group 0 group 1 with group 2 or 3? No, there at least two bits that are different. Thus, next we combine group 1 and group 2. Column II 0 0000 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 0101 0110 1001 1010 11

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 1 and group 2. 0, 1 0, 2 0, 8 1, 5 00000 -0 -000 0 -01 0101 0110 1001 1010 12

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 1 and group 2. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 00000 -0 -000 0 -01 -001 14

Quine-Mc. Cluskey Method An Example Column I Again, there is no need to try to combine group 1 with group 2. Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 24

Quine-Mc. Cluskey Method An Example Column I Again, there is no need to try to combine group 1 with group 3. Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 Lets try to combine group 2 with group 23. group 3 5 6 9 10 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 7 0111 14 1110 25

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 26

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 6, 7 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 011 - 28

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 6, 14 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 011 -110 29

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 6, 14 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 011 -110 30

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 6, 14 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 011 -110 31

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 Combine group 2 and group 3. 0101 0110 1001 1010 0, 1 0, 2 0, 8 1, 5 1, 9 2, 6 2, 10 8, 9 8, 10 5, 7 6, 14 00000 -0 -000 0 -01 -001 0 -10 -010 10010 -0 01 -1 011 -110 32

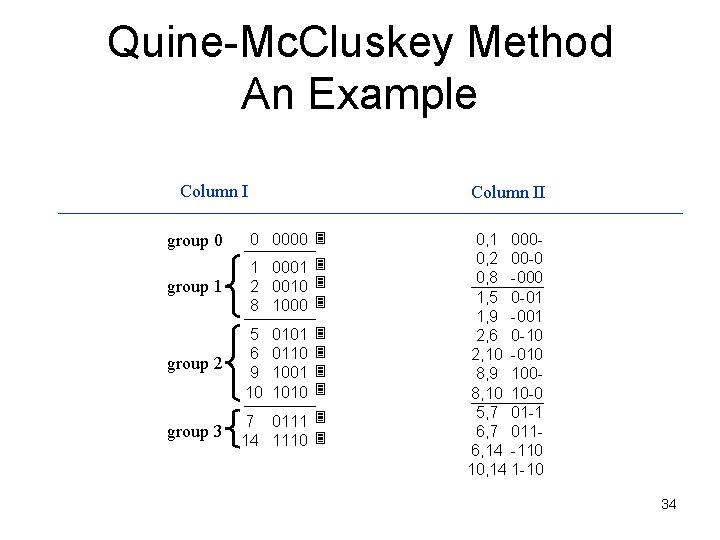
Quine-Mc. Cluskey Method An Example Column I We have now completed the first step. All minterms in column I were included. We can divide column II into groups. Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 33

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 34

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 Column III 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 35

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 0, 1 000 - 0, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 100 - 8, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -00 - 40

Quine-Mc. Cluskey Method An Example Column I group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 5 6 9 10 group 3 7 0111 14 1110 0101 0110 1001 1010 Column III 0, 1 000 - 0, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 100 - 8, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 47

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 0101 0110 1001 1010 group 2 5 6 9 10 group 3 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 0, 8, 1, 9 -00 - 49

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 0, 2, 8, 10 0, 8, 1, 9 0, 8, 2, 10 2, 6, 10, 14 2, 10, 6, 14 -00 -0 -0 --10 No more combinations are possible, thus we stop here. 60

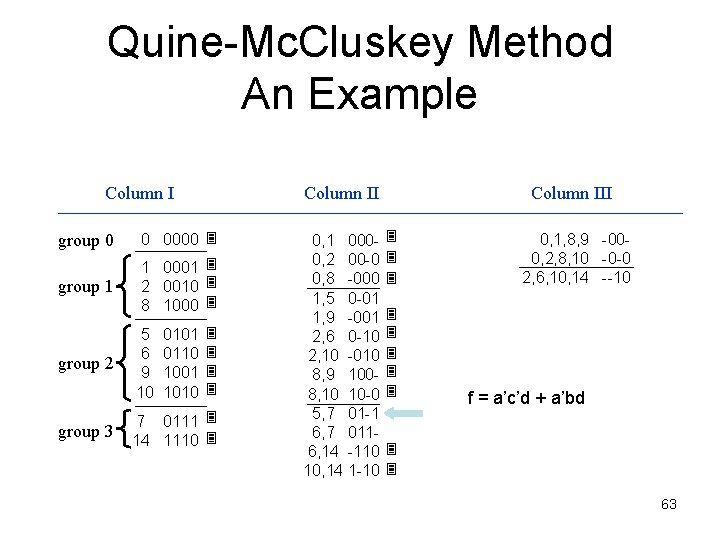
Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 Now we form f with the terms not checked f = a’c’d 62

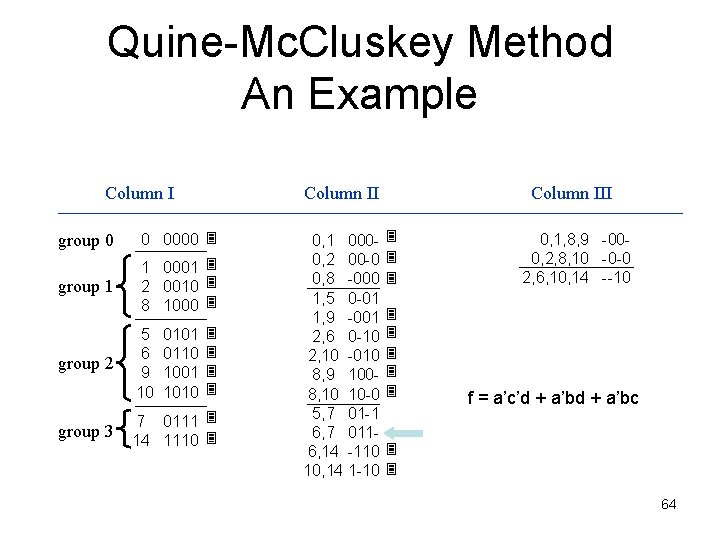
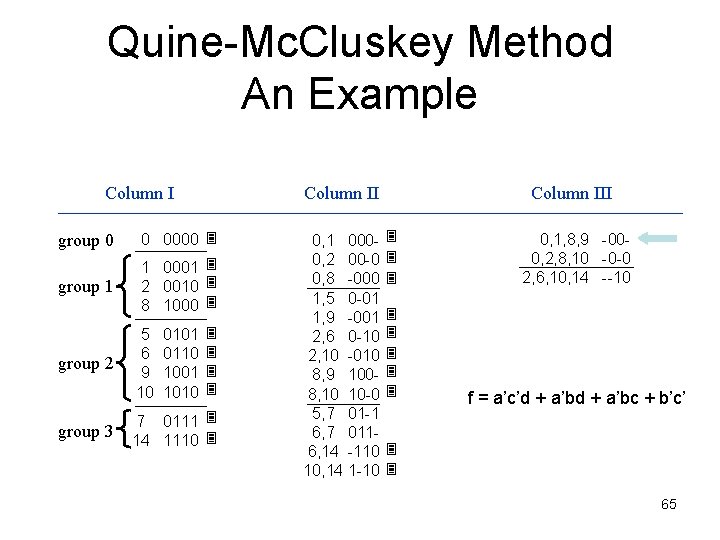
Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 f = a’c’d + a’bd 63

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 f = a’c’d + a’bc 64

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 f = a’c’d + a’bc + b’c’ 65

Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 f = a’c’d + a’bc + b’c’ + b’d’ 66

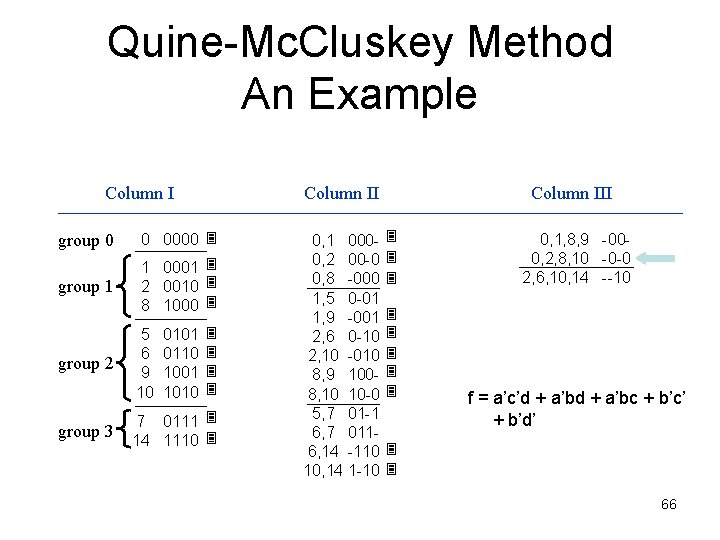
Quine-Mc. Cluskey Method An Example Column II group 0 0 0000 group 1 1 0001 2 0010 8 1000 group 2 group 3 5 6 9 10 0101 0110 1001 1010 7 0111 14 1110 0, 1 0000, 2 00 -0 0, 8 -000 1, 5 0 -01 1, 9 -001 2, 6 0 -10 2, 10 -010 8, 9 1008, 10 10 -0 5, 7 01 -1 6, 7 0116, 14 -110 10, 14 1 -10 Column III 0, 1, 8, 9 -000, 2, 8, 10 -0 -0 2, 6, 10, 14 --10 f = a’c’d + a’bc + b’c’ + b’d’ + cd’ 67

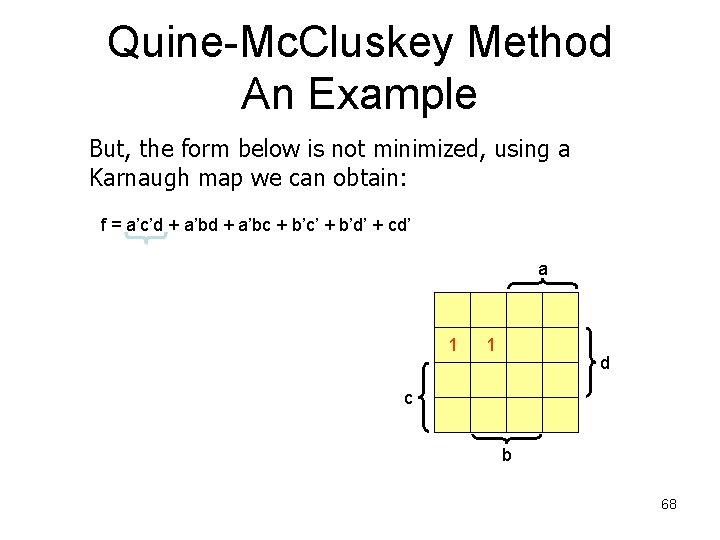
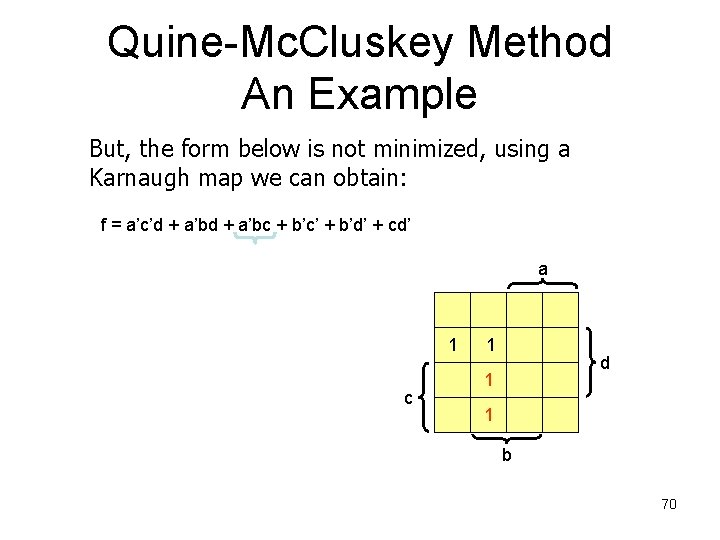
Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 1 d c b 68

Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 c 1 d 1 b 69

Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 c 1 d 1 1 b 70

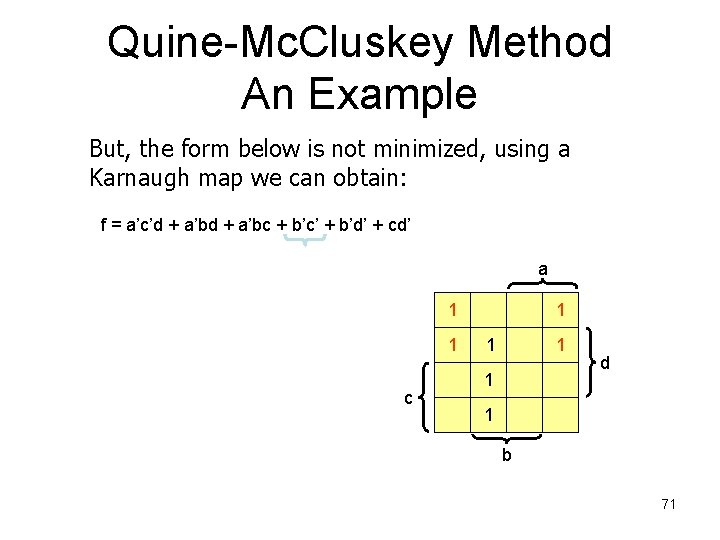
Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 1 c 1 1 d 1 b 71

Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 1 c 1 1 1 d 1 b 72

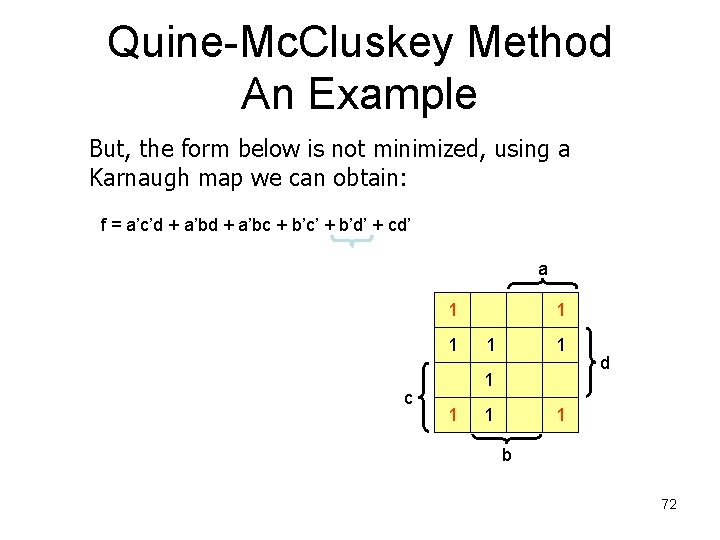
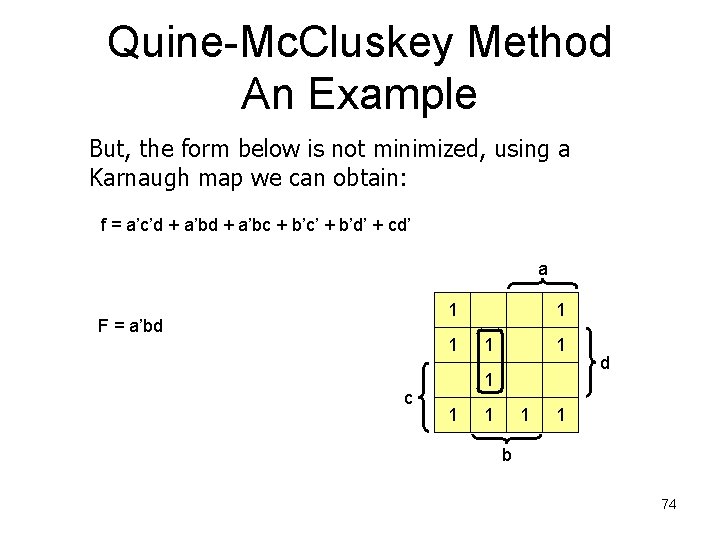
Quine-Mc. Cluskey Method An Example But, the form below is not minimized. Using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 1 c 1 1 1 1 d 1 b 73

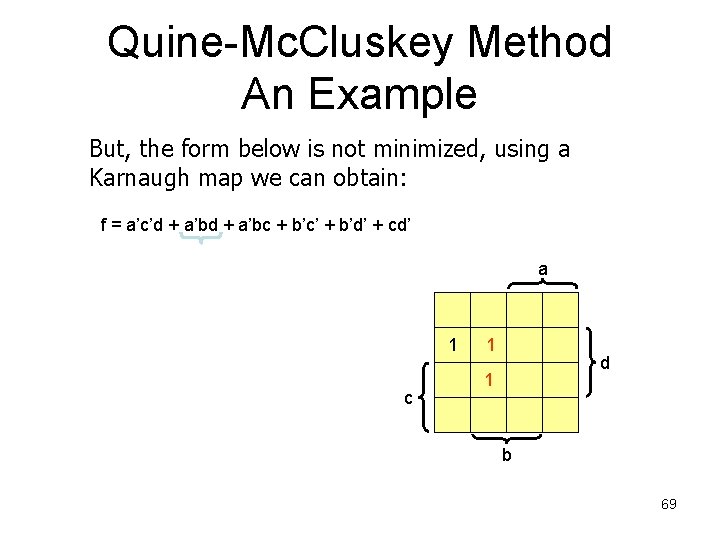
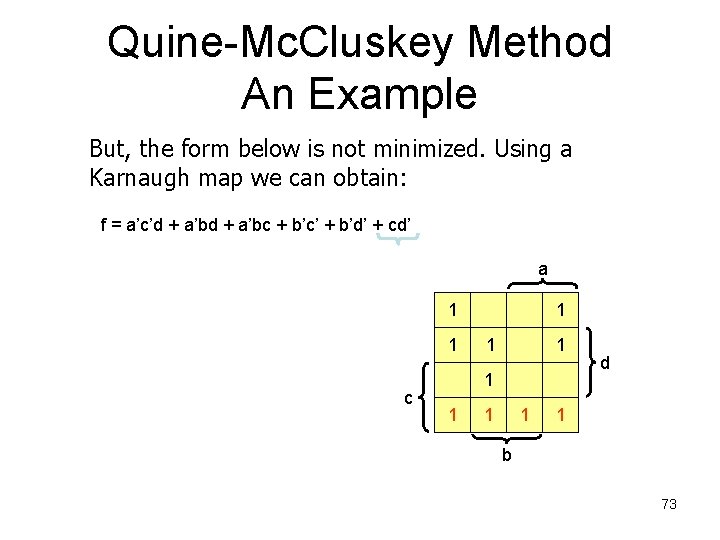
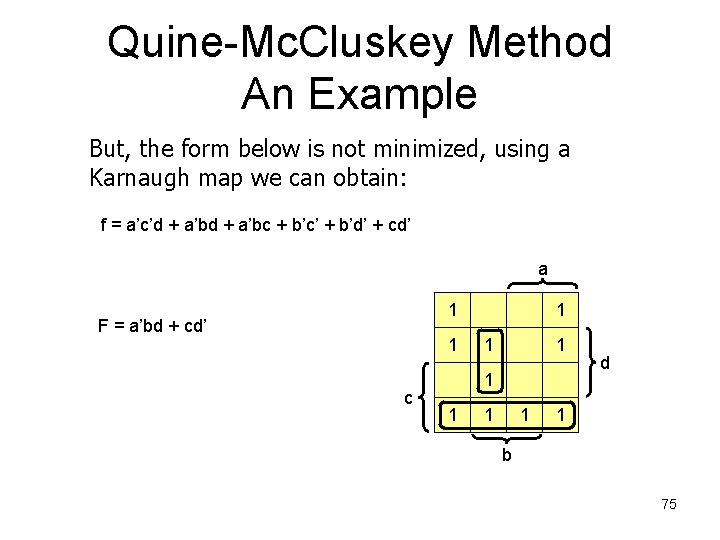
Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 F = a’bd 1 c 1 1 1 1 d 1 b 74

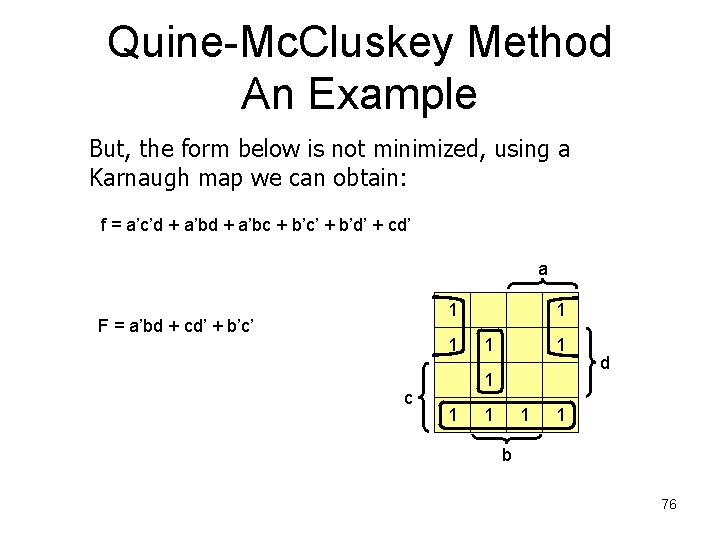
Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 F = a’bd + cd’ 1 c 1 1 1 1 d 1 b 75

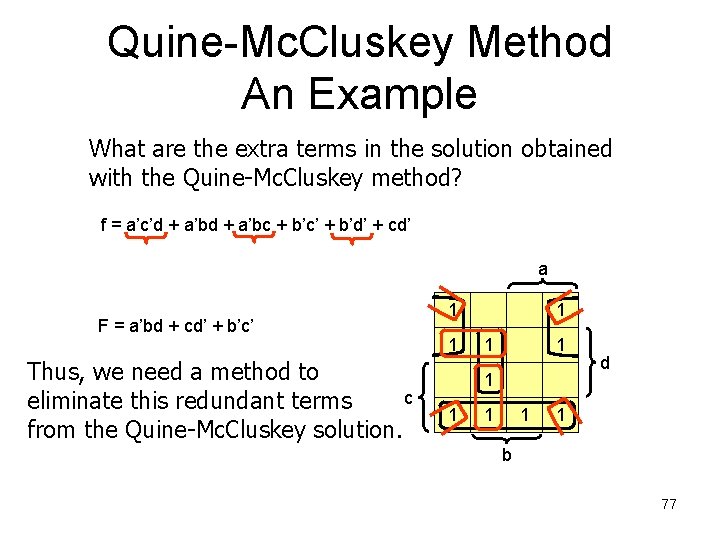
Quine-Mc. Cluskey Method An Example But, the form below is not minimized, using a Karnaugh map we can obtain: f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a 1 F = a’bd + cd’ + b’c’ 1 c 1 1 1 1 d 1 b 76

Quine-Mc. Cluskey Method An Example What are the extra terms in the solution obtained with the Quine-Mc. Cluskey method? f = a’c’d + a’bc + b’c’ + b’d’ + cd’ a F = a’bd + cd’ + b’c’ Thus, we need a method to c eliminate this redundant terms from the Quine-Mc. Cluskey solution. 1 1 1 1 1 d 1 b 77

The Prime Implicant Chart The prime implicant chart is the second part of the Quine-Mc. Cluskey procedure. It is used to select a minimum set of prime implicants. Similar to the Karnaugh map, we first select the essential prime implicants, and then we select enough prime implicants to cover all the minterms of the function. 78

Prime Implicant Chart (Example) Prime Implicants minterms Question: Given the prime implicant chart above, how can we identify the essential prime implicants of the function? 79

Prime Implicant Chart (Example) Prime Implicants minterms Similar to the Karnaugh map, all we have to do is to look for minterms that are covered by a single term. 80

Prime Implicant Chart (Example) Prime Implicants minterms Once a term is included in the solution, all the minterms covered by that term are covered. Therefore we may now mark the covered minterms and find terms that are no longer useful. 81

Prime Implicant Chart (Example) Prime Implicants minterms 82

Prime Implicant Chart (Example) Prime Implicants minterms As we have not covered all the minterms with essential prime implicants, we must choose enough non-essential prime implicants to cover the remaining minterms. 83

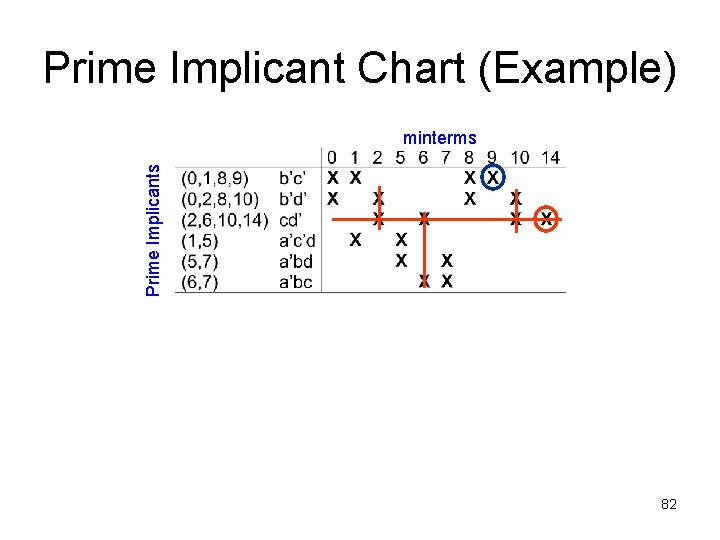
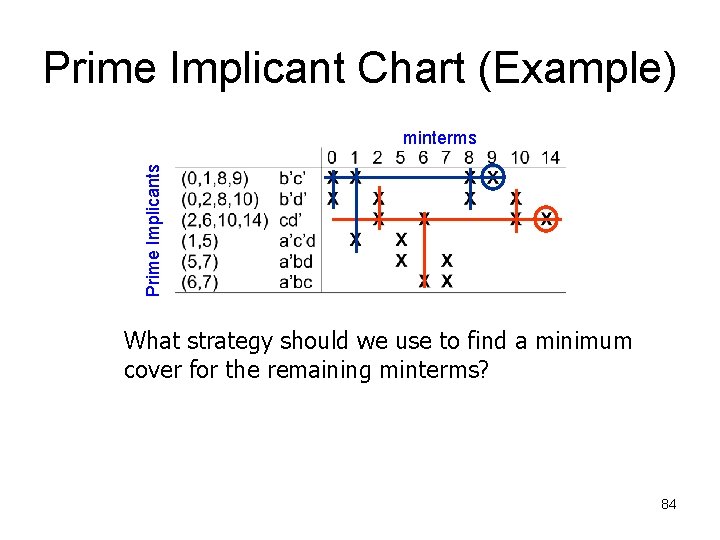
Prime Implicant Chart (Example) Prime Implicants minterms What strategy should we use to find a minimum cover for the remaining minterms? 84

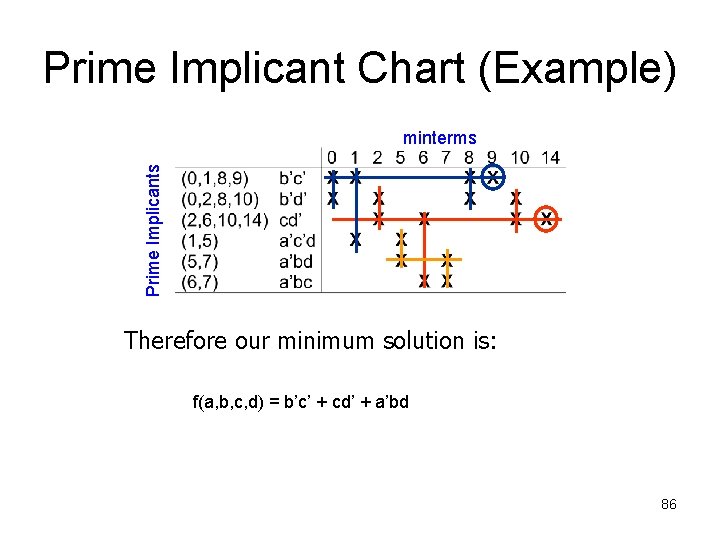
Prime Implicant Chart (Example) Prime Implicants minterms We choose first prime implicants that cover the most minterms. Should this strategy always work? ? 85

Prime Implicant Chart (Example) Prime Implicants minterms Therefore our minimum solution is: f(a, b, c, d) = b’c’ + cd’ + a’bd 86

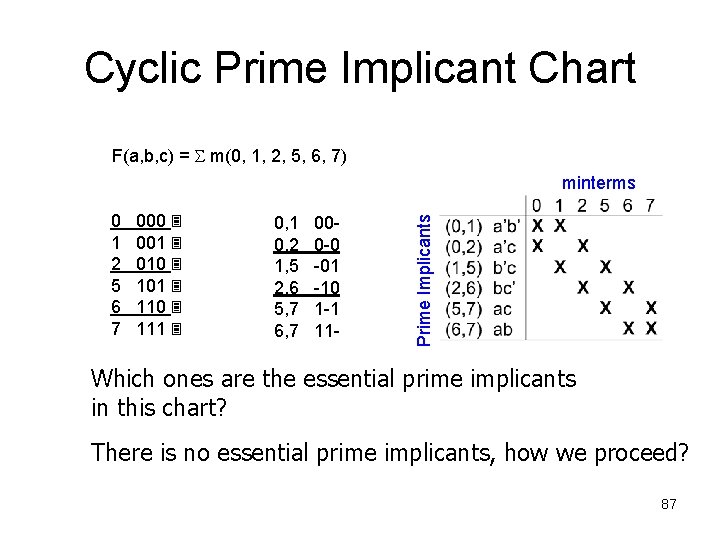
Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7) 0 1 2 5 6 7 000 001 010 101 110 111 0, 1 0, 2 1, 5 2, 6 5, 7 6, 7 000 -0 -01 -10 1 -1 11 - Prime Implicants minterms Which ones are the essential prime implicants in this chart? There is no essential prime implicants, how we proceed? 87

Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7) 0 1 2 5 6 7 000 001 010 101 110 111 0, 1 0, 2 1, 5 2, 6 5, 7 6, 7 000 -0 -01 -10 1 -1 11 - Prime Implicants minterms Also, all implicants cover the same number of minterms. We will have to proceed by trial and error. F(a, b, c) = a’b’ 88

Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7) 0 1 2 5 6 7 000 001 010 101 110 111 0, 1 0, 2 1, 5 2, 6 5, 7 6, 7 000 -0 -01 -10 1 -1 11 - Prime Implicants minterms Thus, we get the minimization: F(a, b, c) = a’b’ + bc’ + ac 90

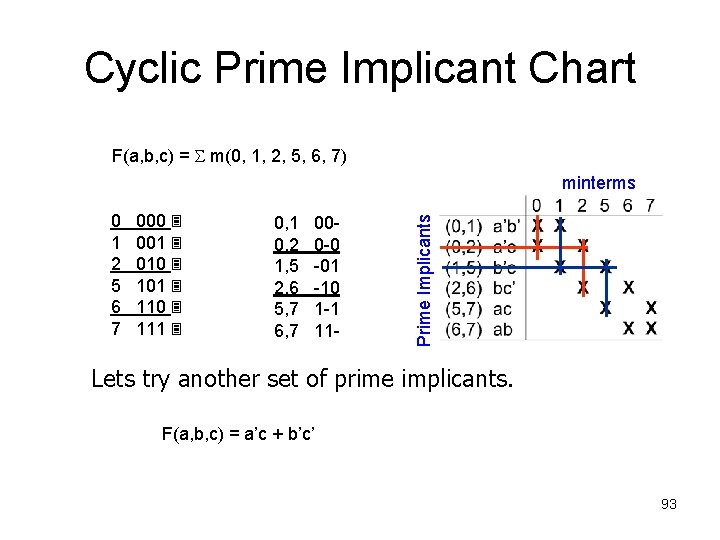
Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7) 0 1 2 5 6 7 000 001 010 101 110 111 0, 1 0, 2 1, 5 2, 6 5, 7 6, 7 000 -0 -01 -10 1 -1 11 - Prime Implicants minterms Lets try another set of prime implicants. 91

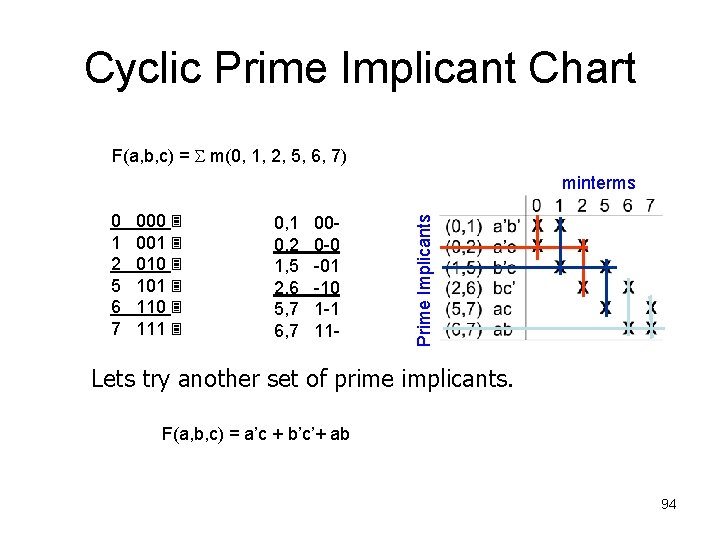
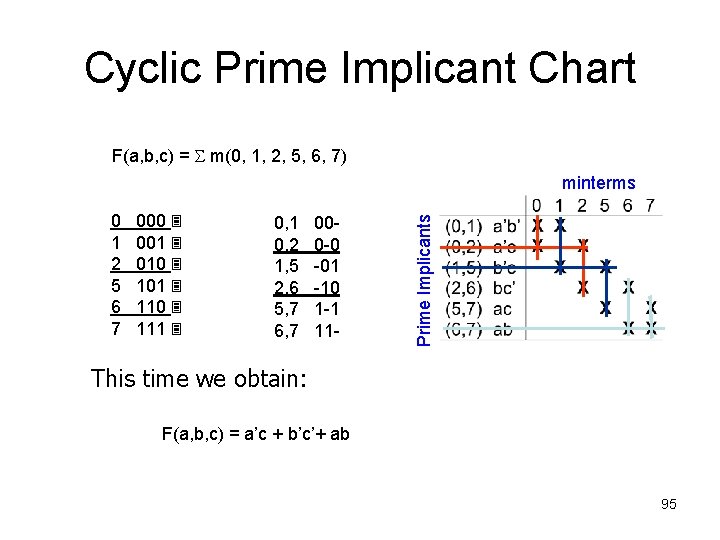
Cyclic Prime Implicant Chart F(a, b, c) = m(0, 1, 2, 5, 6, 7) 0 1 2 5 6 7 000 001 010 101 110 111 0, 1 0, 2 1, 5 2, 6 5, 7 6, 7 000 -0 -01 -10 1 -1 11 - Prime Implicants minterms This time we obtain: F(a, b, c) = a’c + b’c’+ ab 95

Cyclic Prime Implicant Chart F(a, b, c) = a’b’ + bc’ + ac F(a, b, c) = a’c + b’c’+ ab Which minimal form is better? Depends on what terms we must form for other functions that we must also implement. Often we are interested in examining all minimal forms for a given function. Thus we need an algorithm to do so. 96

Petrick’s Method S. R. Petrick. A direct determination of the irredundant forms of a boolean function from the set of prime implicants. Technical Report AFCRC-TR-56 -110, Air Force Cambridge Research Center, Cambridge, MA, April, 1956. Goal: Given a prime implicant chart, determine all minimum sum-of-products solutions. 97

Petrick’s Method An Example Prime Implicants minterms Step 1: Label all the rows in the chart. Step 2: Form a logic function P with the logic variables P 1, P 2, P 3 that is true when all the minterms in the chart are covered. 98

Petrick’s Method An Example Prime Implicants minterms The first column has an X in rows P 1 and P 2. Therefore we must include one of these rows in order to cover minterm 0. Thus the following term must be in P: (P 1 + P 2) 99

Petrick’s Method An Example Prime Implicants minterms Following this technique, we obtain: P = (P 1 + P 2) (P 1 + P 3) (P 2 + P 4) (P 3 + P 5) (P 4 + P 6) (P 5 + P 6) P = (P 1 + P 2) (P 1 + P 3) (P 4 + P 2) (P 5 + P 3) (P 4 + P 6) (P 5 + P 6) P = (P 1 + P 2) (P 1 + P 3) (P 4 + P 2) (P 4 + P 6) (P 5 + P 3) (P 5 + P 6) P = (P 1 + P 2 P 3) (P 4 + P 2 P 6) (P 5 + P 3 P 6) 100

Petrick’s Method An Example P = (P 1 + P 2) (P 1 + P 3) (P 2 + P 4) (P 3 + P 5) (P 4 + P 6) (P 5 + P 6) P = (P 1 + P 2) (P 1 + P 3) (P 4 + P 2) (P 5 + P 3) (P 4 + P 6) (P 5 + P 6) P = (P 1 + P 2) (P 1 + P 3) (P 4 + P 2) (P 4 + P 6) (P 5 + P 3) (P 5 + P 6) P = (P 1 + P 2 P 3) (P 4 + P 2 P 6) (P 5 + P 3 P 6) P = (P 1 P 4 + P 1 P 2 P 6 + P 2 P 3 P 4 + P 2 P 3 P 6) (P 5 + P 3 P 6) P = P 1 P 4 P 5 + P 1 P 2 P 5 P 6 + P 2 P 3 P 4 P 5 + P 2 P 3 P 5 P 6 + P 1 P 3 P 4 P 6 + P 1 P 2 P 3 P 6 + P 2 P 3 P 4 P 6 + P 2 P 3 P 6 P = P 1 P 4 P 5 + P 1 P 2 P 5 P 6 + P 2 P 3 P 4 P 5 + P 1 P 4 P 3 P 6 + P 2 P 3 P 6 101

Petrick’s Method An Example P = P 1 P 4 P 5 + P 1 P 2 P 5 P 6 + P 2 P 3 P 4 P 5 + P 1 P 4 P 3 P 6 + P 2 P 3 P 6 This expression says that to cover all the minterms we must include the terms in line P 1 and line P 4 and line P 5, or we must include line P 1, and line P 2, and line P 5, and line P 6, or … Considering that all the terms P 1, P 2, … have the same cost, how many minimal forms the function has? The two minimal forms are F = a’b’ + bc’ + ac P 1 P 4 P 5 and P 2 P 3 P 6: F = a’c’ + b’c + ab 102