Math 285 Project Diffusion Maps Xiaoyan Chong Department

Math 285 Project Diffusion Maps Xiaoyan Chong Department of Mathematics and Statistics San Jose State University

Outline • Motivation • Algorithm • Implement on toy data and real data • Comparison with other dimensional reduction techniques • Future work

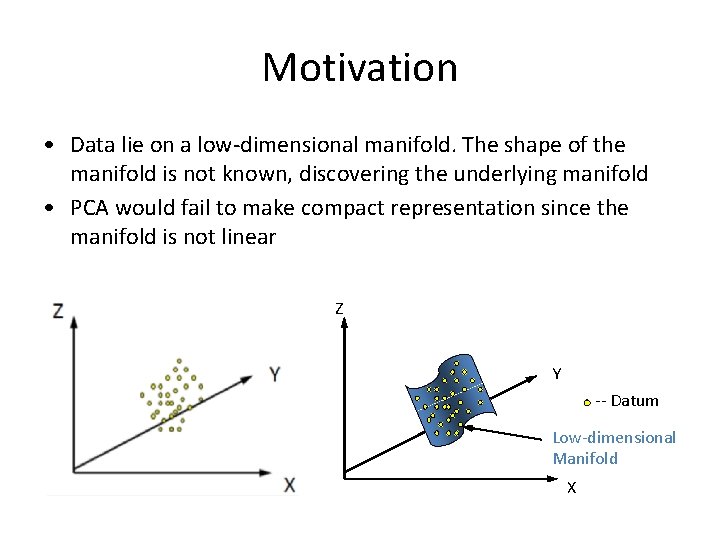
Motivation • Data lie on a low-dimensional manifold. The shape of the manifold is not known, discovering the underlying manifold • PCA would fail to make compact representation since the manifold is not linear Z Y -- Datum Low-dimensional Manifold X

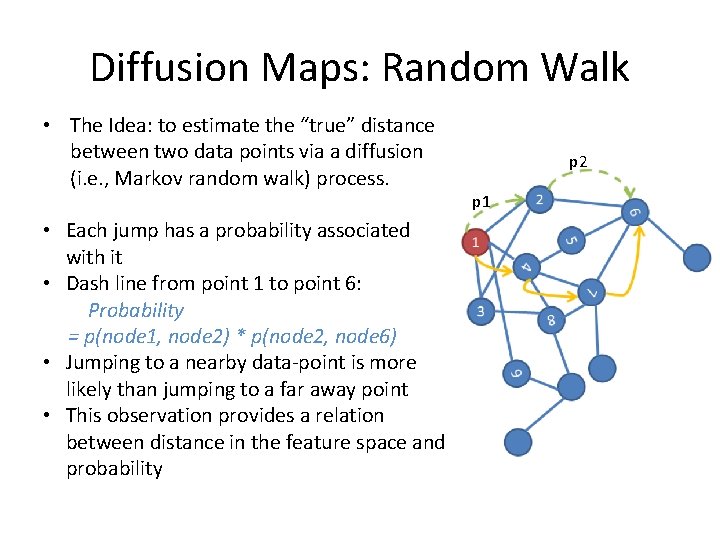
Diffusion Maps: Random Walk • The Idea: to estimate the “true” distance between two data points via a diffusion (i. e. , Markov random walk) process. • Each jump has a probability associated with it • Dash line from point 1 to point 6: Probability = p(node 1, node 2) * p(node 2, node 6) • Jumping to a nearby data-point is more likely than jumping to a far away point • This observation provides a relation between distance in the feature space and probability p 2 p 1

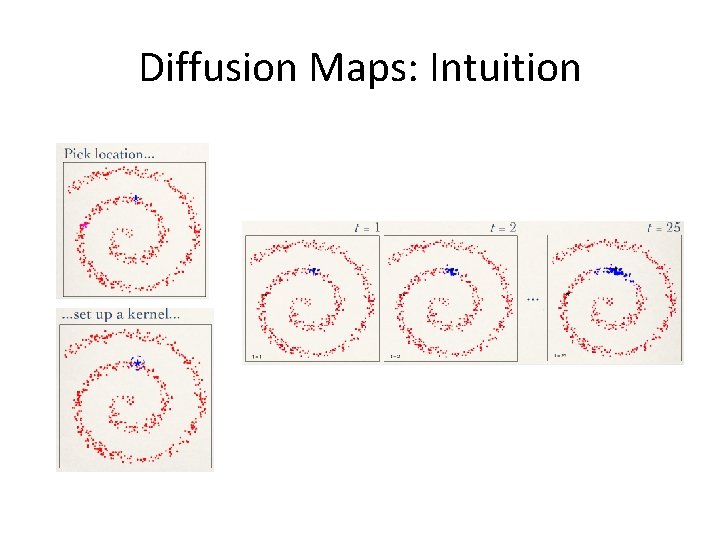
Diffusion Maps: Intuition

Diffusion Maps: The Math (I) • Diffusion kernel: (The kernel indicates a local measure of similarity within a certain neighborhood ) • Compute “one-step” probabilities, and normalized it (in row) • Diffusion matrix P, with entries Pij = p(Xi, Xj) • The probability of stepping from i to j in t step is PT – With increased values of t, the probability of following a path along the underlying geometric structure of the data set increases. -- Along the geometric structure, points are dense and therefore highly connected. Pathways form along short, high probability jumps

Diffusion Maps: The Math (II) • Diffusion distance is defined as: - Calculating diffusion distance is computationally expensive - Consider to map data points into a Euclidean space • Diffusion map: -- using it for reducing dimension, and preserving the diffusion distance. -- The diffusion distance can be expressed in terms of the eigenvectors and eigenvalues of diffusion matrix P The set of orthogonal eigenvectors of P form a basis for the diffusion space, and the associated eigenvalues indicate the importance of each dimension -- Dimensional reduction is achieved by retaining the m dimensions associated with the dominant eigenvectors

Diffusion Maps Algorithm ² INPUT: High dimensional data set Xi 1. Construct similarity graph (kernel) 2. Create diffusion matrix by normalizing the rows of the kernel matrix 3. Calculate the eigenvectors of the diffusion matrix 4. Map points to the d-dimensional diffusion space at time t, using d dominant eigenvectors and eigenvalues ² Output: Low dimensional dataset Yi

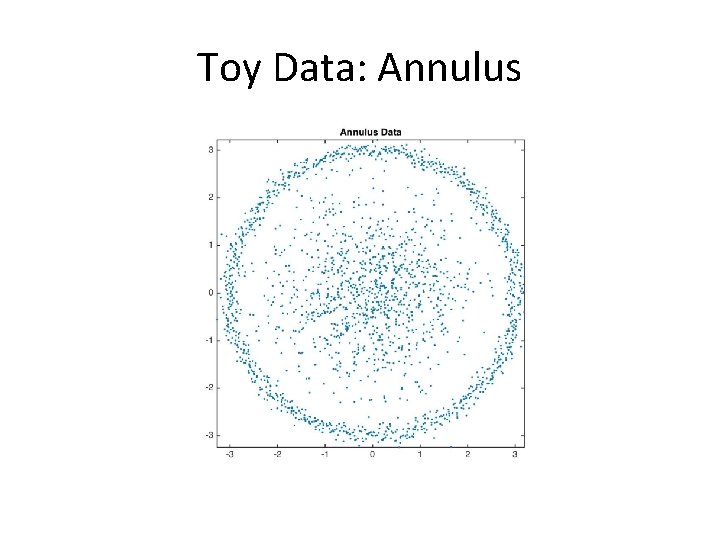
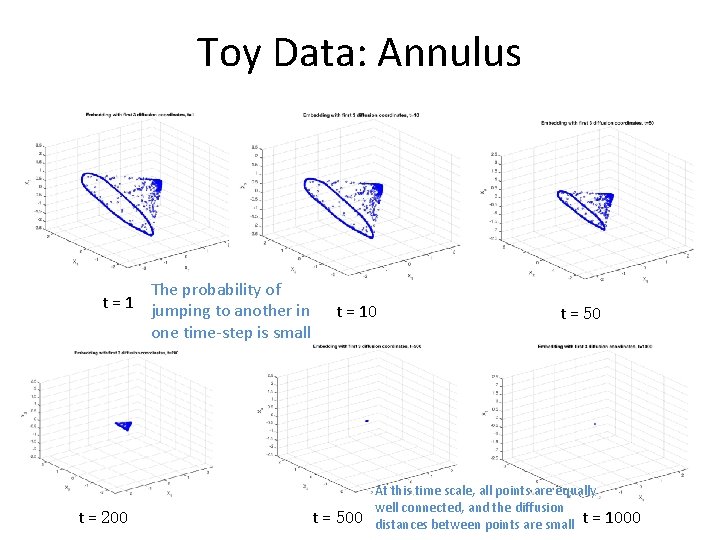
Toy Data: Annulus

Toy Data: Annulus The probability of t = 1 jumping to another in one time-step is small t = 200 t = 10 t = 50 At this time scale, all points are equally well connected, and the diffusion distances between points are small t = 1000

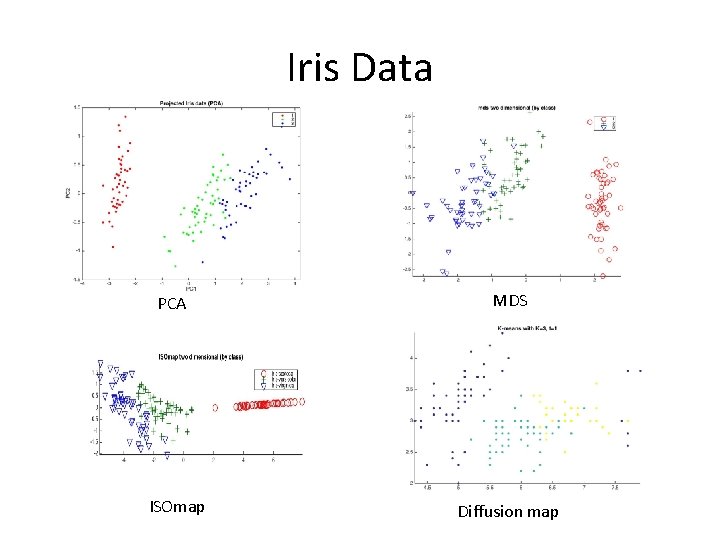
Methods Comparison • Principal Component(PCA) – Linear structure • Multidimensional Scaling (MDS) – Linear; Euclidean Distance • Isomap – Nonlinear; Geodesic Distance, not robust to noise • Diffusion Maps – Nonlinear (The technique is robust to noise perturbation and is computationally inexpensive)

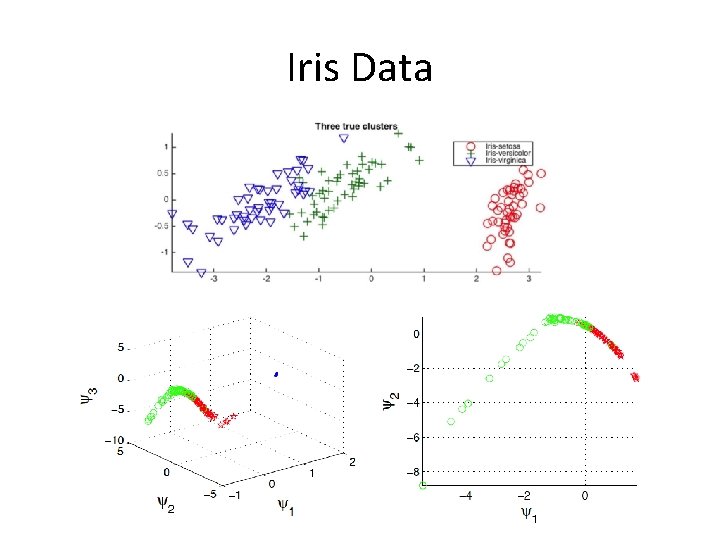
Iris Data

Iris Data PCA MDS ISOmap Diffusion map

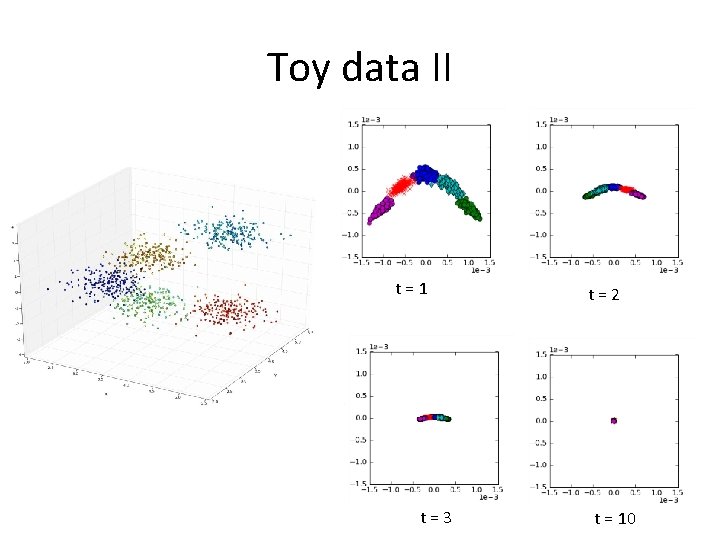
Toy data II t=1 t=3 t=2 t = 10

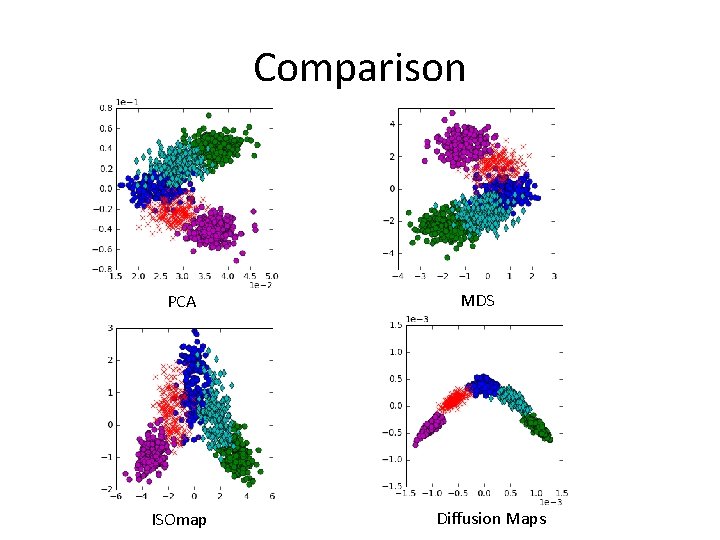
Comparison PCA ISOmap MDS Diffusion Maps

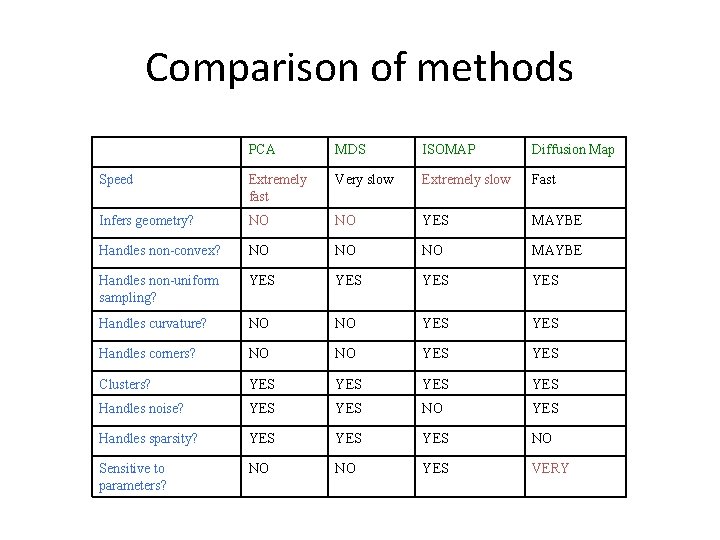
Comparison of methods PCA MDS ISOMAP Diffusion Map Speed Extremely fast Very slow Extremely slow Fast Infers geometry? NO NO YES MAYBE Handles non-convex? NO NO NO MAYBE Handles non-uniform sampling? YES YES Handles curvature? NO NO YES Handles corners? NO NO YES Clusters? YES YES Handles noise? YES NO YES Handles sparsity? YES YES NO Sensitive to parameters? NO NO YES VERY

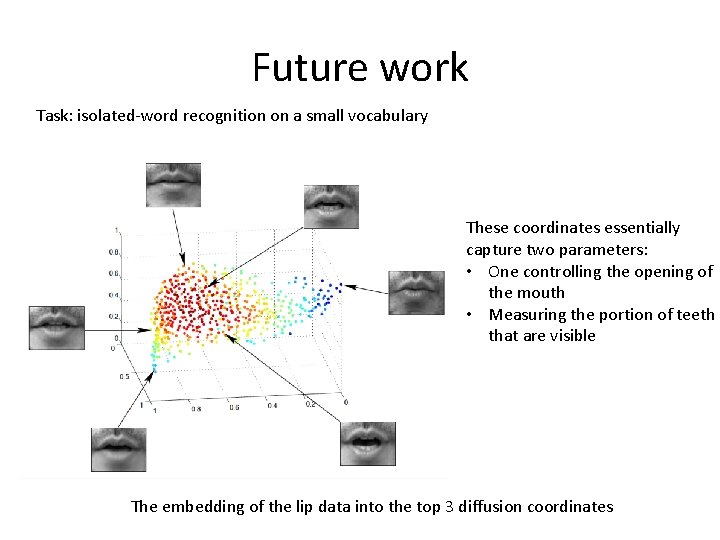
Future work Task: isolated-word recognition on a small vocabulary These coordinates essentially capture two parameters: • One controlling the opening of the mouth • Measuring the portion of teeth that are visible The embedding of the lip data into the top 3 diffusion coordinates

Thank you