Mcanique des fluides 1re partie Olivier LOUISNARD Centre






















































- Slides: 84

Mécanique des fluides 1ère partie Olivier LOUISNARD Centre Poudres et Procédés Bureau 1 C 6 – tel 30 62 Email : louisnar@enstimac. fr

Plan du cours Séance de cours C 1 C 2 C 3 C 4 C 5 C 6 Chapitre poly Généralités. Définitions. Forces sur un fluide Hydrostatique Equations de conservation Mouvement d’un fluide Cas du fluide parfait incompressible Forces exercées par un fluide sur une structure Pertes et gains de charge. Pompes et turbines 1 - 4 4 2 et 3 5 6 3 et 5 6

Cours connexes Prérequis Analyse vectorielle Mécanique Thermodynamique En parallèle Phénomènes de transferts Thermodynamique et procédés Mécanique des milieux continus Suite Mécanique des fluides 2ème partie Transferts convectifs (Option énergétique)

Prérequis Mathématiques Mécanique Loi de la dynamique Thermodynamique Premier principe (= conservation de l’énergie)

Qu’est-ce qu’un fluide ? • pas de forme propre • s’écoule si on lui applique une force • prend la forme du récipient Les molécules interagissent (peu pour les gaz) Gardent une certaine mobilité les unes par rapport aux autres. Pas d’ordre comme dans un solide (ou peu) Limite solide / fluide parfois floue : • dépend de la dynamique de la sollicitation (sable mouillé, polymères, pâtes) • états semi-ordonnés (ou « indécis » ) (liquides vitreux, cristaux liquides, colloides) • dépend de l’échelle de temps considérée (glacier)

Quelques fluides Monophasiques eau, air, huile, métaux fondus Multiphasiques • aérosols (brouillard) • émulsions (lait, vinaigrette, anisette. . . ) • suspensions (pâtes, boues) • liquides à bulles (surface de l’océan, fluides de refroidissement) « Complexes » • magma, plasmas, ferrofluides (propriétés magnétiques) • polymères, micelles, cristaux liquides (molécules 1 D ou 2 D. . . ) • milieux granulaires (sable, poudres)

Ferrofluides Cristaux liquides Lait Liquide à bulles

Description d’un fluide Macroscopique : celle qui nous intéresse • à notre échelle • milieu continu (? ) Microscopique • atomes ou molécules + ou - libres les uns / aux autres • Liquide = fort encombrement / interactions forte • Gaz = faible encombrement / interaction faible On cherche à représenter ce que l’on voit : description macroscopique

Analogie Echelle macro (la notre) Méso Echelle micro

Hypothèse de milieu continu Comment définir une densité r et une vitesse v variant continument / x, y, z ? Masse volumique r(x, y, z) = ? (kg/m 3) (x, y, z) Echelle macroscopique Masse volumique (kg/m 3) Vitesse v(x, y, z) = ? mi Echelle mésoscopique Echelle microscopique Champ de vitesses r et v grandeurs continues (et dérivables. . . ) / à x, y, z Pas toujours vrai. . (ondes de chocs, vides poussés)

Grandeurs volumiques G(t) grandeur extensive contenue dans V On définit : soit g grandeur volumique (G/m 3) Masse de fluide dans V Quantité de mouvement de V Energie cinétique de V Energie interne de V grandeurs globales grandeurs locales Remarque : V peut être fixe ou mobile (par rapport à nous)

Masse volumique r(x, y, z) en kg/m 3 En général différente d’un point à un autre Eau 1000 kg/m 3 Mercure 13000 kg/m 3 Air 1. 3 kg /m 3 Varie avec la température (même pour un liquide) Varie avec la pression (peu pour un liquide) Une approximation bien utile : le fluide incompressible r = r 0 constant par rapport à t et x, y, z Conditions de validité : plus tard Masse de fluide dans V

Forces exercées sur un fluide Forces surfaciques ou « de contact » exercées sur chaque élément de surface d. S (pression, frottement visqueux) Forces volumiques exercées sur chaque élément de volume d. V (poids, forces d’inertie, magnétiques, . . . )

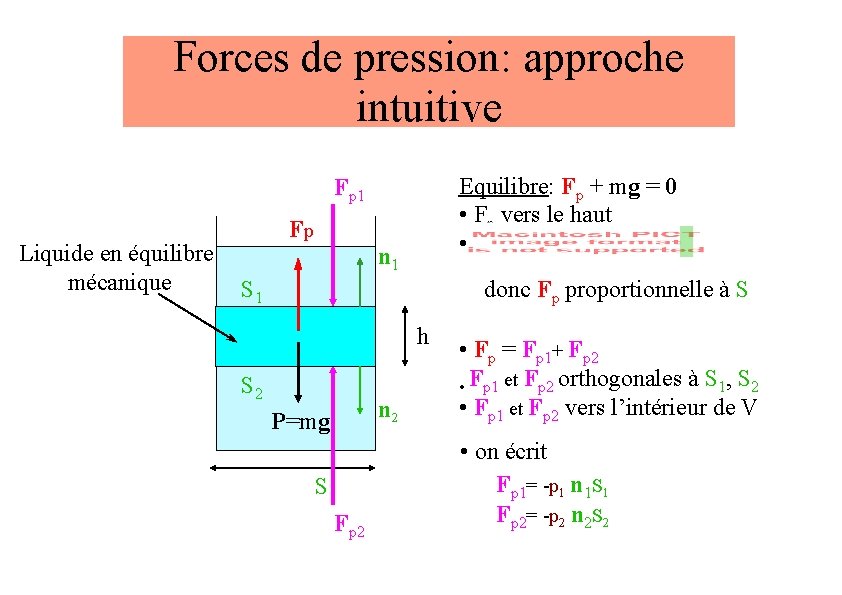
Forces de pression: approche intuitive Equilibre: Fp + mg = 0 • Fp vers le haut • Fp 1 Liquide en équilibre mécanique S 1 Fp n 1 donc Fp proportionnelle à S h S 2 n 2 P=mg S Fp 2 • Fp = Fp 1+ Fp 2 • Fp 1 et Fp 2 orthogonales à S 1, S 2 • Fp 1 et Fp 2 vers l’intérieur de V • on écrit Fp 1= -p 1 n 1 S 1 Fp 2= -p 2 n 2 S 2

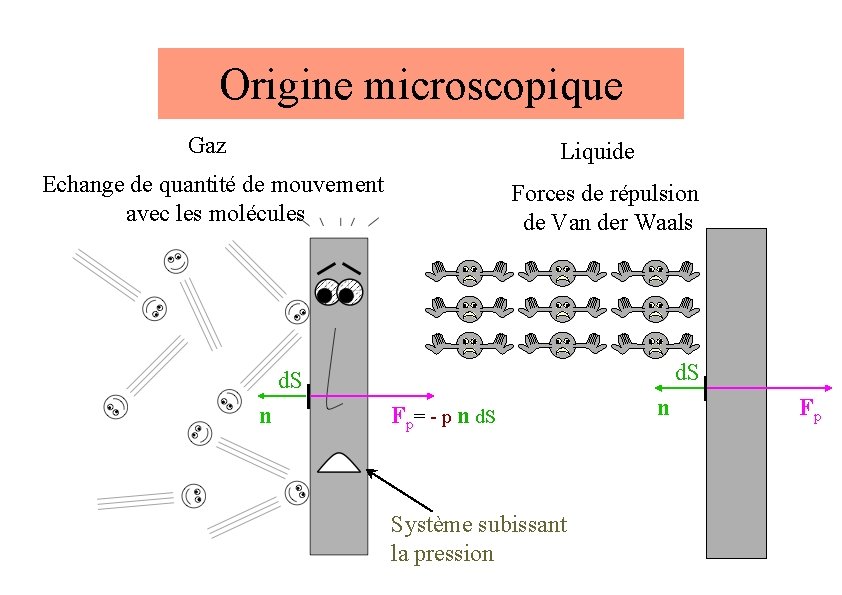
Origine microscopique Gaz Liquide Echange de quantité de mouvement avec les molécules Forces de répulsion de Van der Waals d. S n Fp= - p n d. S Système subissant la pression n Fp

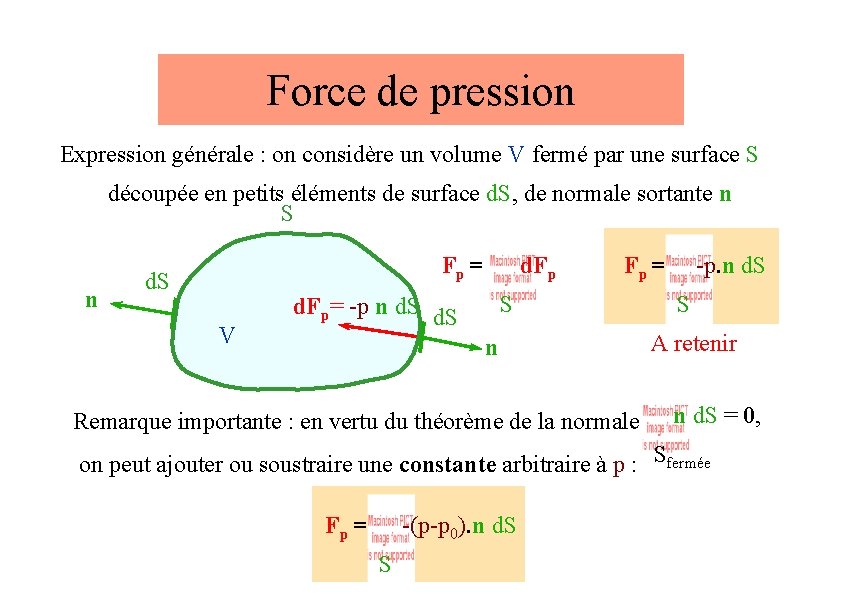
Force de pression Expression générale : on considère un volume V fermé par une surface S découpée en petits éléments de surface d. S, de normale sortante n S n Fp = d. S V d. Fp Fp = S d. Fp= -p n d. S n Remarque importante : en vertu du théorème de la normale -p. n d. S S A retenir n d. S = 0, on peut ajouter ou soustraire une constante arbitraire à p : Sfermée Fp = -(p-p 0). n d. S S

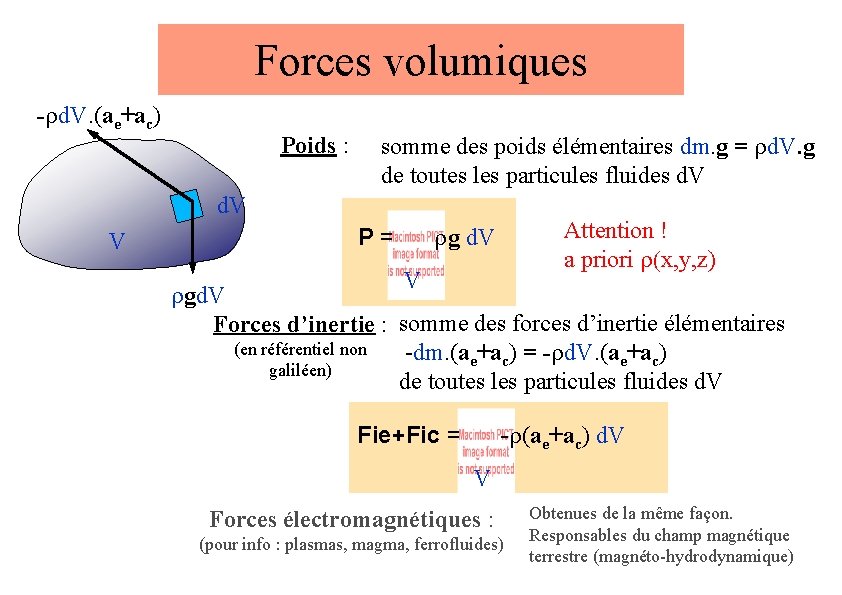
Forces volumiques -rd. V. (ae+ac) Poids : somme des poids élémentaires dm. g = rd. V. g de toutes les particules fluides d. V V Attention ! a priori r(x, y, z) rg d. V P= V rgd. V Forces d’inertie : somme des forces d’inertie élémentaires (en référentiel non -dm. (ae+ac) = -rd. V. (ae+ac) galiléen) de toutes les particules fluides d. V Fie+Fic = -r(ae+ac) d. V V Forces électromagnétiques : (pour info : plasmas, magma, ferrofluides) Obtenues de la même façon. Responsables du champ magnétique terrestre (magnéto-hydrodynamique)

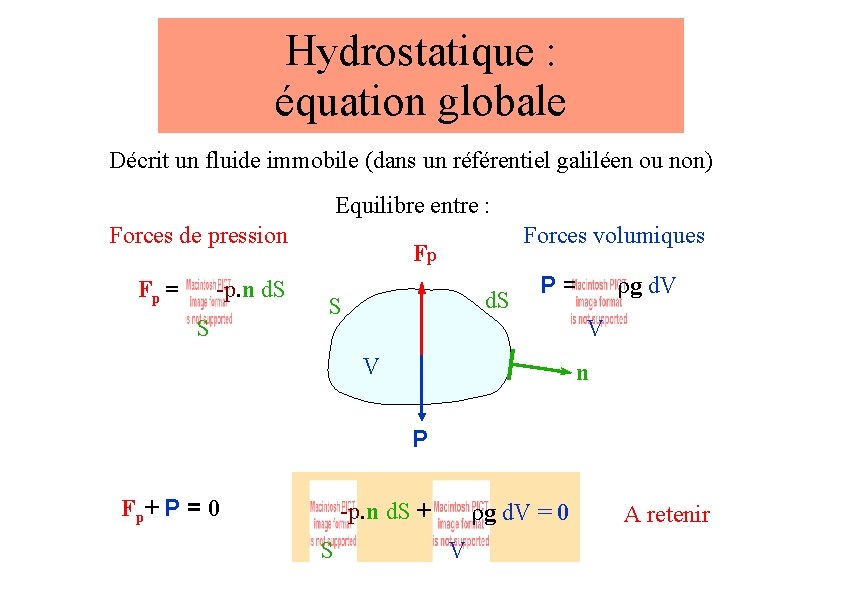
Hydrostatique : équation globale Décrit un fluide immobile (dans un référentiel galiléen ou non) Equilibre entre : Forces de pression Fp = -p. n d. S S Forces volumiques Fp d. S S rg d. V P= V V n P Fp+ P = 0 rg d. V = 0 -p. n d. S + S V A retenir

Hydrostatique : équation globale • La résultante des forces de pression est toujours dirigée vers le haut c’est la poussée d’Archimède ! • Equation peu pratique pour calculer le champ de pression Il faut la réécrire sous forme « locale » = exprimée en tout point grâce à des opérateurs d’analyse vectorielle.

Hydrostatique : équation locale rg d. V = 0 -p. n d. S + S V Or (formule de Green): -p. n d. S = S Donc : V rg d. V = 0, vrai quel que soit V -grad p d. V + V L’intégrande doit être nul, soit -grad p d. V V grad p = rg A retenir

Hydrostatique : équation locale grad p = rg • Peut être intégrée pour trouver le champ de pression p(x, y, z) dans un fluide au repos • Condition aux limites : p = patm sur la surface de contact avec l’air • Les surfaces isobares p(x, y, z) = Cte sont perpendiculaires à g • La pression augmente quand on se dirige dans le sens de g (c’est le problème du plongeur) • La pression diminue quand on se dirige en sens inverse de g (mal de l’altitude, pressurisation des cabines d’avion)

Hydrostatique en référentiel non galiléen Le fluide est immobile par rapport à un référentiel R’ qui accélère / R • une cuve ou un verre dans un véhicule qui freine/accélère (ae horizontal) • miroirs liquides (cf. TD), centrifugeuses (ae radial) • expériences en gravité 0 (ae = g) Il faut ajouter la force d’inertie d’entraînement La force de Coriolis est nulle car le fluide est immobile Fie = -rae d. V Fic = 0 V Fp+ P + Fie= 0 r(g - ae)d. V = 0 -p. n d. S + S V Tout revient à remplacer g par la « pesanteur apparente » g - ae

Hydrostatique en référentiel non galiléen Sous forme globale : S Sous forme locale : r(g -ae) d. V = 0 -p. n d. S + V grad p = r (g -ae) Les surfaces isobares p(x, y, z) = Cte sont maintenant perpendiculaires à g-ae

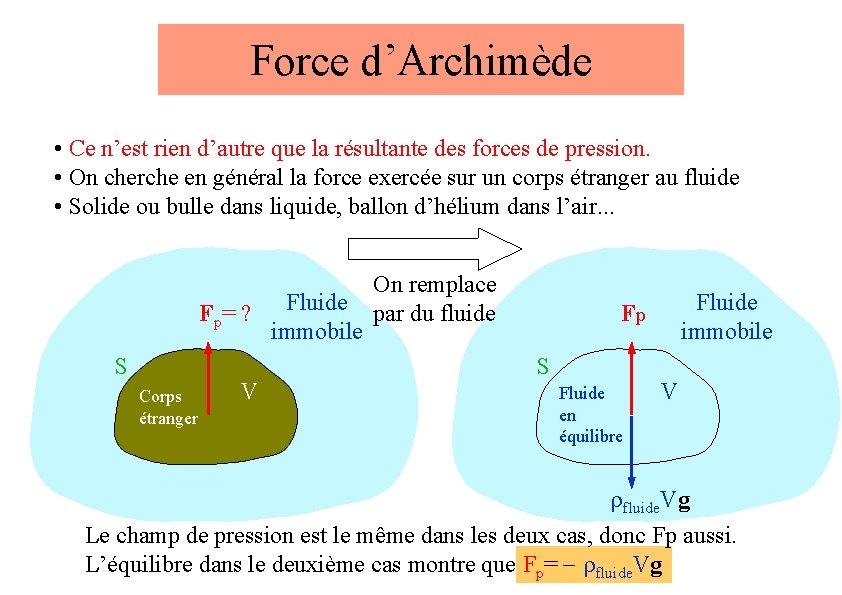
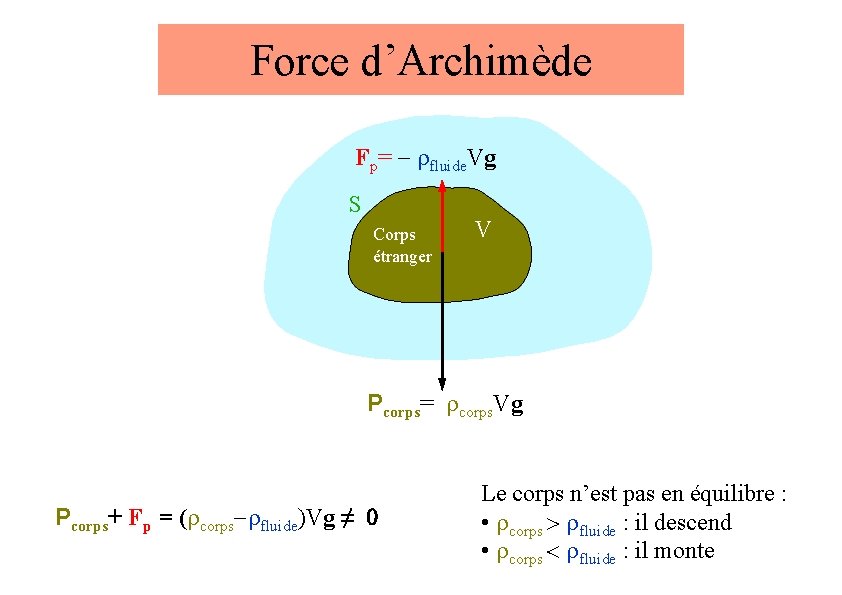
Force d’Archimède • Ce n’est rien d’autre que la résultante des forces de pression. • On cherche en général la force exercée sur un corps étranger au fluide • Solide ou bulle dans liquide, ballon d’hélium dans l’air. . . Fp= ? S Corps étranger V Fluide immobile On remplace par du fluide Fluide immobile Fp S Fluide en équilibre V rfluide. Vg Le champ de pression est le même dans les deux cas, donc Fp aussi. L’équilibre dans le deuxième cas montre que Fp= - rfluide. Vg

Force d’Archimède Fp= - rfluide. Vg S Corps étranger V Pcorps= rcorps. Vg Pcorps+ Fp = (rcorps-rfluide)Vg ≠ 0 Le corps n’est pas en équilibre : • rcorps > rfluide : il descend • rcorps < rfluide : il monte

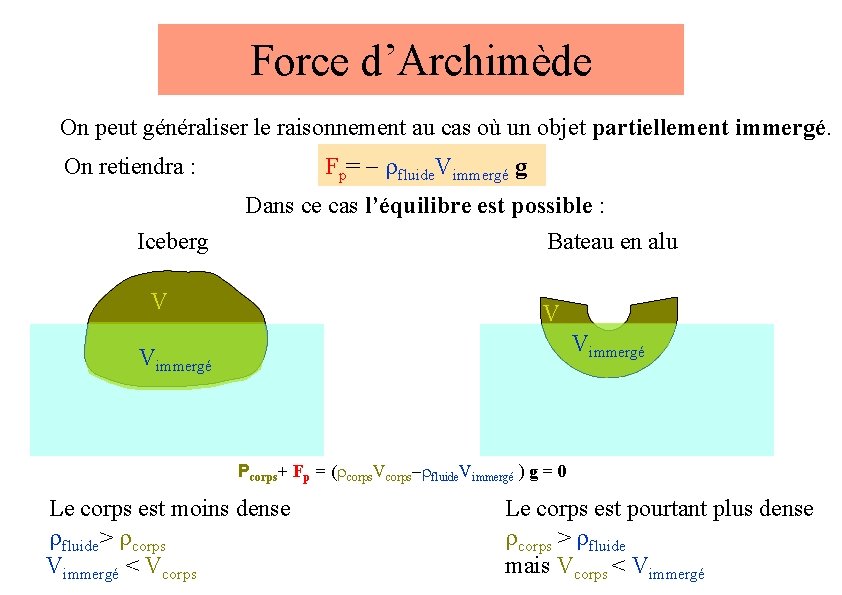
Force d’Archimède On peut généraliser le raisonnement au cas où un objet partiellement immergé. On retiendra : Iceberg Fp= - rfluide. Vimmergé g Dans ce cas l’équilibre est possible : Bateau en alu V V Vimmergé Pcorps+ Fp = (rcorps. Vcorps-rfluide. Vimmergé ) g = 0 Le corps est moins dense rfluide> rcorps Vimmergé < Vcorps Le corps est pourtant plus dense rcorps > rfluide mais Vcorps < Vimmergé

Densité On définit la densité d’un corps d = rcorps/ reau si solide ou liquide d = rcorps / rair(20°C, 1 atm) si gaz

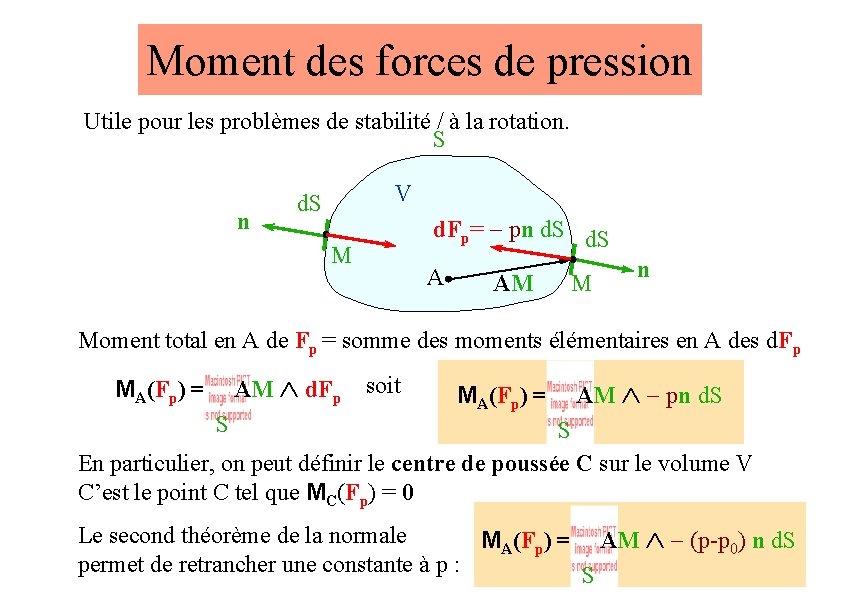
Moment des forces de pression Utile pour les problèmes de stabilité / à la rotation. S n V d. S d. Fp= - pn d. S M A AM M n Moment total en A de Fp = somme des moments élémentaires en A des d. Fp MA(Fp) = AM d. Fp S MA(Fp) = AM - pn d. S S En particulier, on peut définir le centre de poussée C sur le volume V C’est le point C tel que MC(Fp) = 0 soit Le second théorème de la normale MA(Fp) = AM - (p-p 0) n d. S permet de retrancher une constante à p : S

Rappel sur les unités Masse volumique r, unité SI : kg / m 3 Pression p : • unité SI : N / m 2 = kg m-1 s-2 = Pa (Pascal) • 1 bar = 100 k. Pa • 1 torr = 1 mm Hg • . 1 psi = 1 pound / square inch Pression atmosphérique : 1 atm = 1, 01325 bar = 101325 Pa = 760 torr = 14, 70 psi

Exercices d’application de l’hydrostatique • Intégration de l’équation de l’hydrostatique - dans un liquide incompressible - dans l’atmosphère - dans en liquide en référentiel non galiléen • Mesure de la densité avec un tube en U • Force de pression et moment sur une paroi de bassin

Principes de conservation La nature conserve plusieurs grandeurs : • la masse • la quantité de mouvement • l’énergie « Rien ne se perd, rien ne se crée »

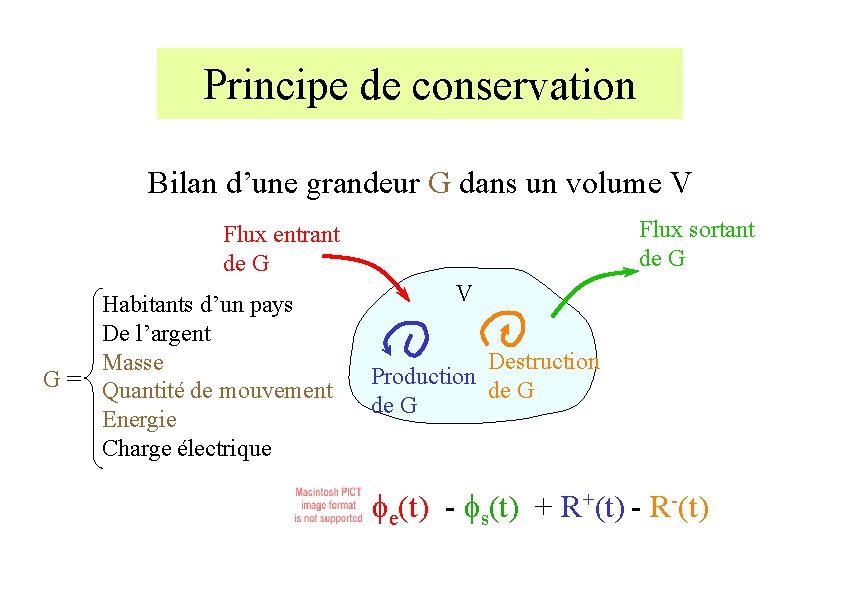
Principe de conservation Bilan d’une grandeur G dans un volume V Flux sortant de G Flux entrant de G Habitants d’un pays De l’argent Masse G = Quantité de mouvement Energie Charge électrique V Destruction Production de G fe(t) - fs(t) + R+(t) - R-(t)

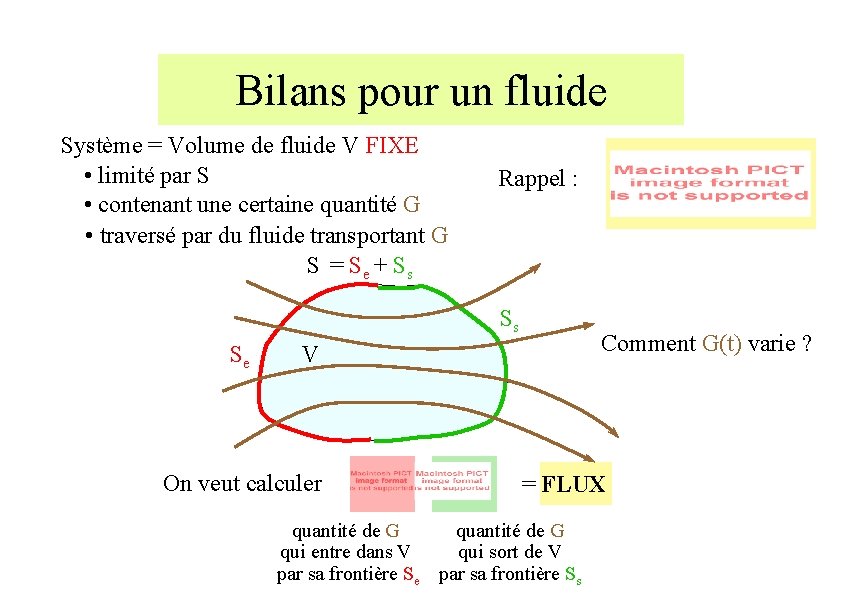
Bilans pour un fluide Système = Volume de fluide V FIXE • limité par S • contenant une certaine quantité G • traversé par du fluide transportant G S = Se + Ss Rappel : Ss Se Comment G(t) varie ? V On veut calculer = FLUX quantité de G qui entre dans V qui sort de V par sa frontière Se par sa frontière Ss

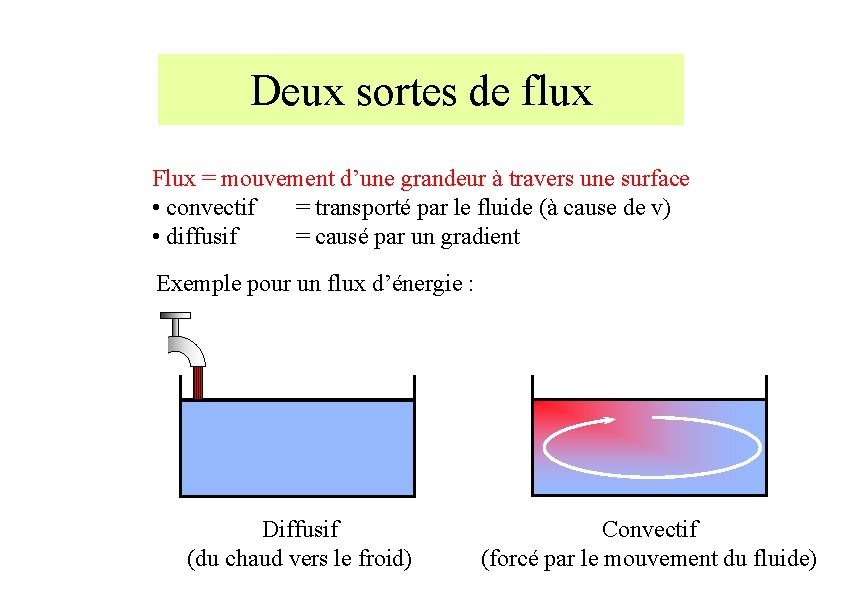
Deux sortes de flux Flux = mouvement d’une grandeur à travers une surface • convectif = transporté par le fluide (à cause de v) • diffusif = causé par un gradient Exemple pour un flux d’énergie : Diffusif (du chaud vers le froid) Convectif (forcé par le mouvement du fluide)

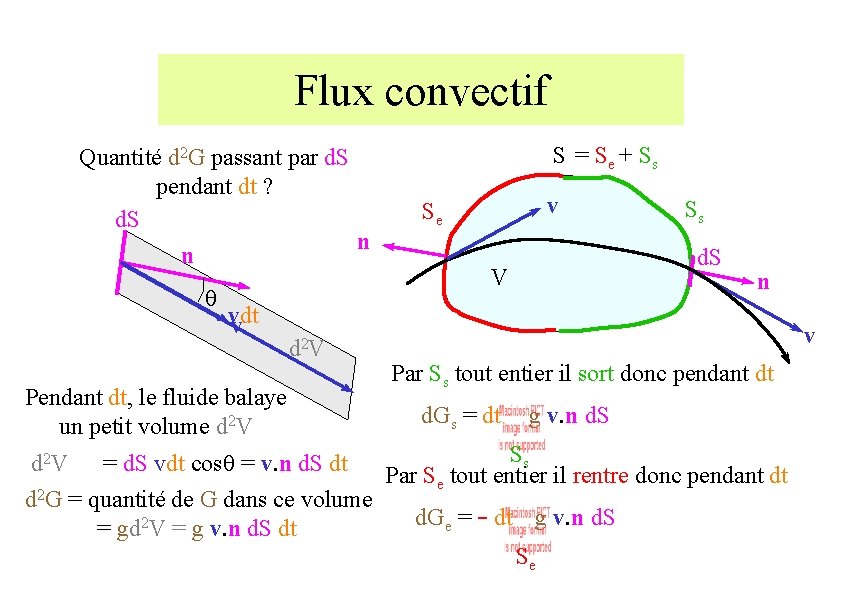
Flux convectif Quantité d 2 G passant par d. S pendant dt ? d. S n n q vdt v Pendant dt, le fluide balaye un petit volume d 2 V S = Se + Ss v Se Ss d. S V n v Par Ss tout entier il sort donc pendant dt d. Gs = dt g v. n d. S Ss d 2 V = d. S vdt cosq = v. n d. S dt Par Se tout entier il rentre donc pendant dt d 2 G = quantité de G dans ce volume d. Ge = - dt g v. n d. S = gd 2 V = g v. n d. S dt Se

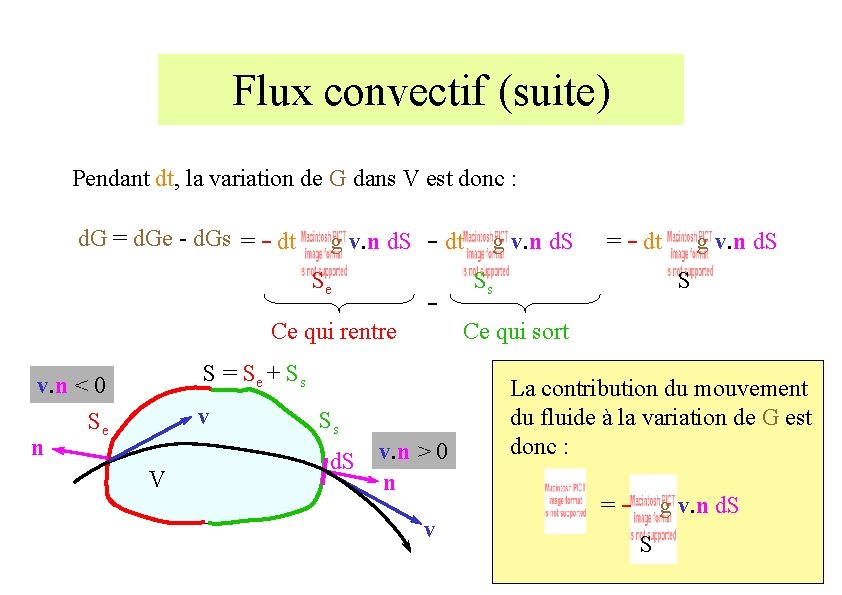
Flux convectif (suite) Pendant dt, la variation de G dans V est donc : d. G = d. Ge - d. Gs = - dt g v. n d. S Se Ce qui rentre - S = Se + Ss v. n < 0 n - dt v Se V Ss d. S v. n > 0 n v g v. n d. S = - dt g v. n d. S S Ss Ce qui sort La contribution du mouvement du fluide à la variation de G est donc : = - g v. n d. S S

Bilan pour un fluide Le bilan de G dans un volume V est donc: G g d. V = V g v. n d. S S + flux diffusifs + création - disparition fe(t) - fs(t) + R+(t) - R-(t) S v n V d. S n v

Bilans sur un tube de courant Objectif : avoir des équations plus simples sans ni S V Le prix à payer : faire des hypothèses simplificatrices v Slat v Tube de courant : n v Se Slat v. n < 0 V Ss v n v v. n = 0 S v g v. n d. S + g v. n d. S Se Ss v. n > 0 v S = Se + Ss + Slat g v. n d. S = n Slat Hypothèses supplémentaires ?

Bilan sur un tube de courant Hypothèse : g uniforme sur Se et Ss (justifié pour des écoulements en conduite) On définit les vitesses moyennes > 0 ve et vs en entrée et en sortie : ve. Se = - v. n d. S vs. Ss = Se Ss v. n d. S = - geve. Se g v. n d. S = ge Se Se n Se v. n < 0 Slat Ss v v V Slat Le bilan sur la grandeur g devient : v. n d. S = + gsvs. Ss g v. n d. S = gs Ss v n v G v. n > 0 v = geve. Se - gsvs. Ss +

Justification tube de courant Ecoulement laminaire Ecoulement turbulent Approximation écoulement piston On définit une vitesse moyenne v sur la section, par : v. n d. S v. S = S

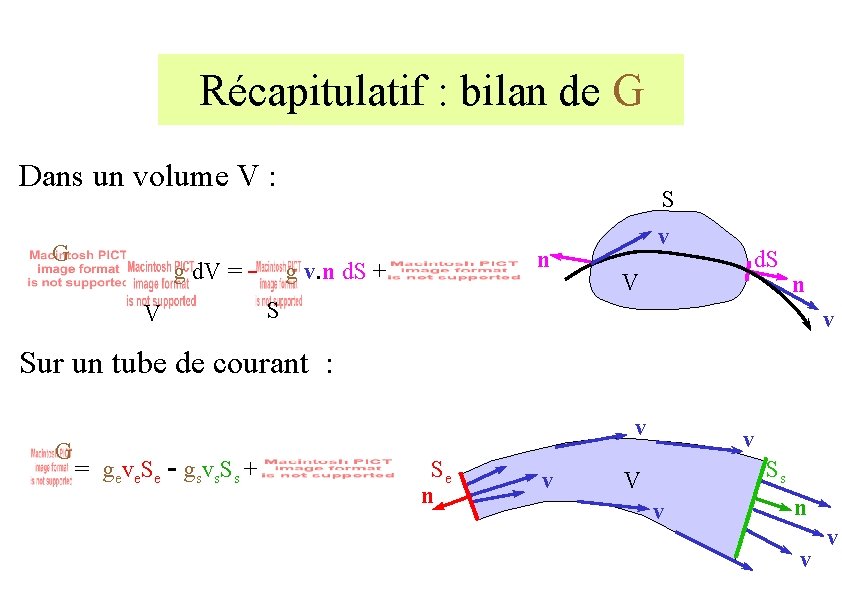
Récapitulatif : bilan de G Dans un volume V : G g d. V = V S n g v. n d. S + v V d. S S n v Sur un tube de courant : G v = geve. Se - gsvs. Ss + Se n v v Ss V v n v v

Bilan de matière • G = M • g = r • R+ - R- = 0 Général : masse volumique ni production, ni destruction, ni flux diffusifs (pour un fluide homogène) M r d. V = S V Tube de courant : M r v. n d. S = reve. Se - rsvs. Ss Me Ms M = rv. S débit massique (noté aussi q)

Conservation de la quantité de mouvement P’ 1=m 1 v’ 1 P 1=m 1 v 1 P 1+ P 2 = P’ 1+ P’ 2 Choc P 2=m 2 v 2 Variation de QDM de 2 : P’ 2 -P 2 = P’ 1 - P 1 = F 1/2 Dt Echange de QDM <=> force : P’ 2=m 2 v’ 2 DP 2 = F 1/2 Dt Une force « produit » de la quantité de mouvement.

Bilan de quantité de mouvement • G = P • g = rv • R+ - R- = S Fext quantité de mouvement densité de quantité de mouvement loi de la dynamique P rv d. V = S V Tube de courant : P rv (v. n) d. S = reve(ve. Se) - rsvs (vs. Ss) Meve Msvs Equations vectorielles

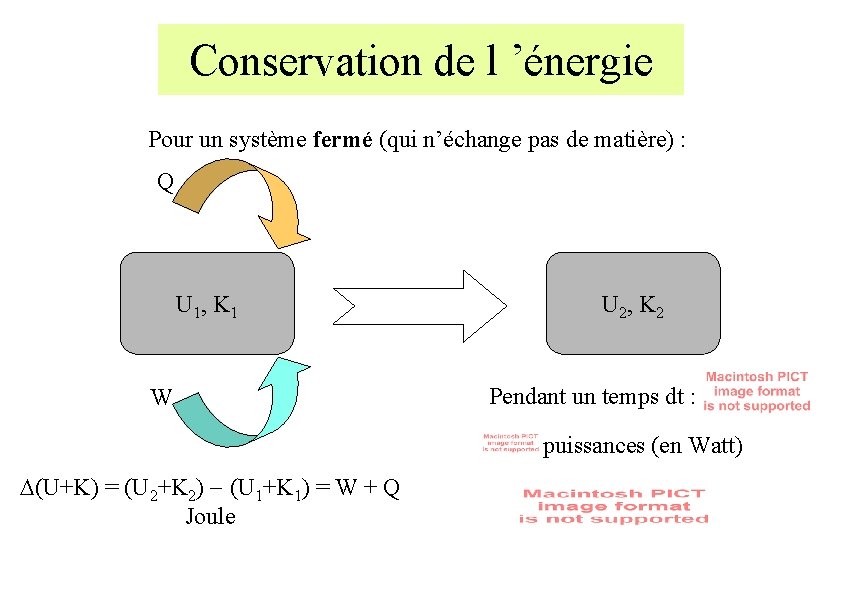
Conservation de l ’énergie Pour un système fermé (qui n’échange pas de matière) : Q U 1, K 1 W U 2, K 2 Pendant un temps dt : puissances (en Watt) D(U+K) = (U 2+K 2) - (U 1+K 1) = W + Q Joule

Bilan d’énergie • G = U+K • g = r (u + v 2/2) • R+ - R- = (U+K) énergie interne + cinétique densité d’énergie interne + cinétique premier principe de la thermo r (u + v 2/2) d. V = S V Tube de courant : (U+K) r (u + v 2/2) (v. n) d. S = re (ue + ve 2/2) (ve. Se) - re (us + vs 2/2) (vs. Ss) Me (ue + ve 2/2) Ms (us + vs 2/2) Le calcul de relève du cours de transfert thermique

Forces extérieures rg d. V Poids : V Pression : -pn d. S S Frottement visqueux : frottement fluide / fluide adhérence fluide aux solides dissipation d’énergie

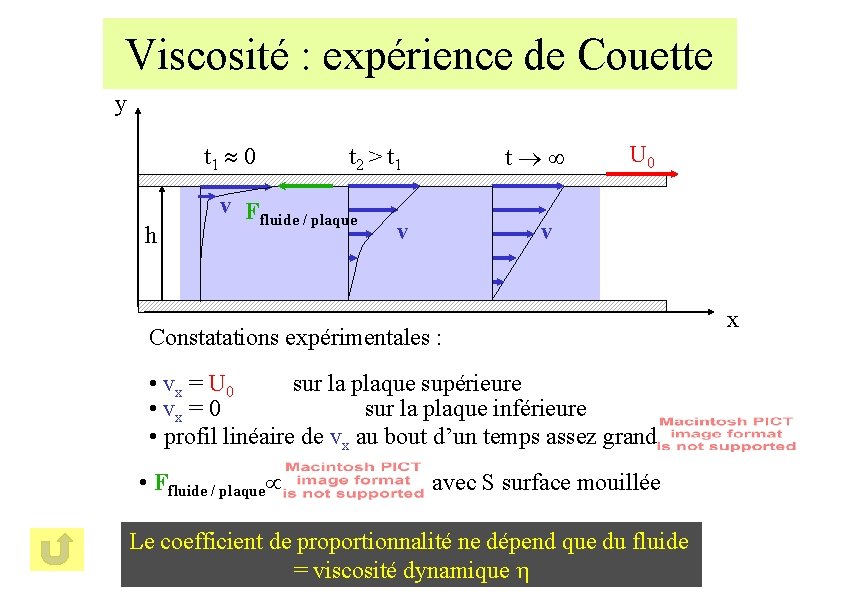
Viscosité : expérience de Couette y t 1 0 h t 2 > t 1 v Ffluide / plaque v t U 0 v Constatations expérimentales : • vx = U 0 sur la plaque supérieure • vx = 0 sur la plaque inférieure • profil linéaire de vx au bout d’un temps assez grand • Ffluide / plaque avec S surface mouillée Le coefficient de proportionnalité ne dépend que du fluide = viscosité dynamique x

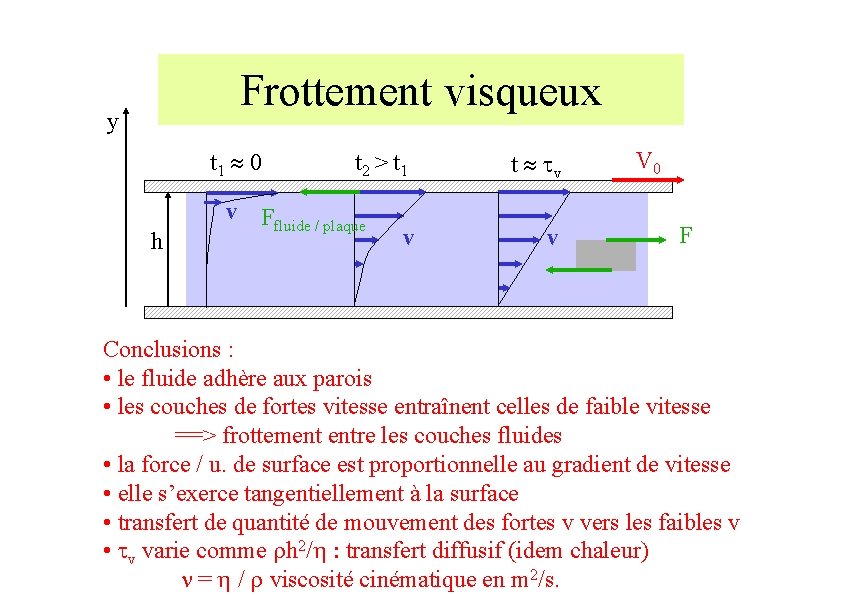
Frottement visqueux y t 1 0 h t 2 > t 1 v Ffluide / plaque v t tv v V 0 F Conclusions : • le fluide adhère aux parois • les couches de fortes vitesse entraînent celles de faible vitesse ==> frottement entre les couches fluides • la force / u. de surface est proportionnelle au gradient de vitesse • elle s’exerce tangentiellement à la surface • transfert de quantité de mouvement des fortes v vers les faibles v • tv varie comme rh 2/ : transfert diffusif (idem chaleur) n = / r viscosité cinématique en m 2/s.

Viscosité • homogène à kg. m-1. s-1 = Pa. s = Pl (Poiseuille) on utilise le Poise (Po) et surtout le Centipoise (c. Po) Eau : 10 -3 Pa. s = 1 c. Po Air : 1. 85 10 -5 Pa. s • augmente avec T pour un gaz indépendant de p pour un gaz diminue avec T pour un liquide (cf. huile dans poële) augmente avec p pour un liquide

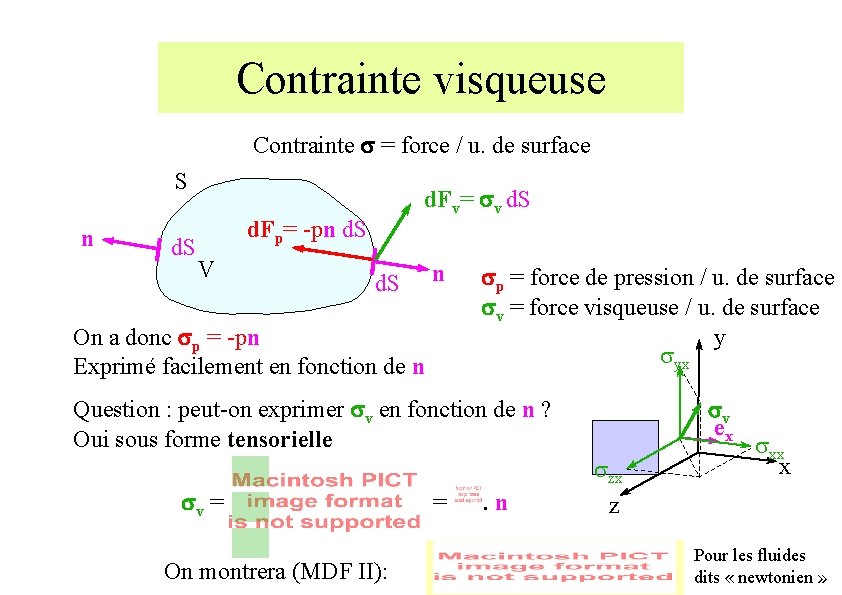
Contrainte visqueuse Contrainte s = force / u. de surface S n d. S d. Fv= sv d. S d. Fp= -pn d. S V d. S On a donc sp = -pn Exprimé facilement en fonction de n n sp = force de pression / u. de surface sv = force visqueuse / u. de surface y syx sv ex Question : peut-on exprimer sv en fonction de n ? Oui sous forme tensorielle sv = On montrera (MDF II): = . n szx z sxx x Pour les fluides dits « newtonien »

Bilan de quantité de mouvement rv d. V = V Variation de QDM du fluide dans le volume V S QDM transportée par le fluide rentrant - sortant -pn d. S + . n d. S rg d. V + rv (v. n) d. S + S S V Poids Pression Frottement visqueux

Equations locales Objectif : remplacer le bilan sur un volume V par des relations différentielles valables en chaque point du fluide Moyens : • théorèmes S V • passage à la limite V 0 Intérêt : • calcul analytique ou numérique de solutions d’écoulement

Les équations locales Masse masse volumique pression QDM énergie interne vitesse Energie Système complet ? 1 équation vectorielle 2 équations scalaires + 2 équations scalaires Il manque une équation d’état : 1 inconnue vectorielle 3 inconnues scalaires + 1 inconnue scalaire

Quelques équations d’état Gaz parfait : (compresseurs, turbines à gaz) GP isotherme : (rare) GP isentropique : (acoustique, ondes de chocs, écoulements gazeux en général) Liquide compressible : (explosions sous-marines, écoulements liquides supersoniques, rare) Fluide incompressible : (hydraulique, presque tous les écoulements liquide + écoulements gaz faible Mach) BAROTROPES Equation de l’énergie découplée de M et QDM

Autres écritures s’écrit aussi ou encore = a accélération du fluide

Bilan matière pour un fluide incompressible r( x, y, z, t) = r 0 Général v. n d. S = 0 S n Se V S = Se + Ss v Ss d. S n v Tube de courant ve. Se = vs. Ss Ve Equation locale Vs Ce qui rentre = Ce qui sort Accumulation de masse impossible V = v. S débit volumique (noté aussi Q)

Validité fluide incompressible Correct si : c vitesse du son dans le fluide Exemple pour un gaz parfait: Ma = nombre de Mach déduite de l’équation d’état = 340 m/S à 298 K • Validité indépendante du caractère gazeux ou liquide • Inutilisable si Ma > 0, 3 • Inutilisable pour rendre compte de certains phénomènes (acoustique, chocs) • En pratique presque toujours valable dans les liquides

Modèle de fluide parfait Permet de négliger les frottements visqueux • mouvement non dissipatif • conservation de l’énergie mécanique • pas d’adhérence aux parois solides • pas de création de « rotationnel » • ouvre de nombreuses simplifications mathématiques Limitations évidentes. Ne rend pas compte : • du freinage visqueux d’un corps ou d’un fluide (voiture économique !) • de l’amortissement des ondes (vagues, acoustiques, . . . ) Validité ?

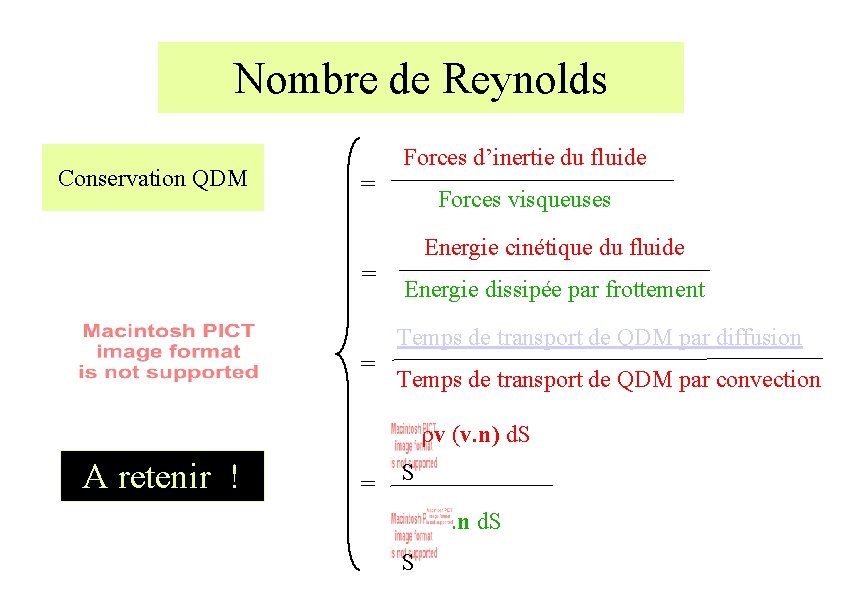
Nombre de Reynolds Conservation QDM Forces d’inertie du fluide = Forces visqueuses Energie cinétique du fluide = Energie dissipée par frottement Temps de transport de QDM par diffusion = Temps de transport de QDM par convection rv (v. n) d. S A retenir ! = S . n d. S S

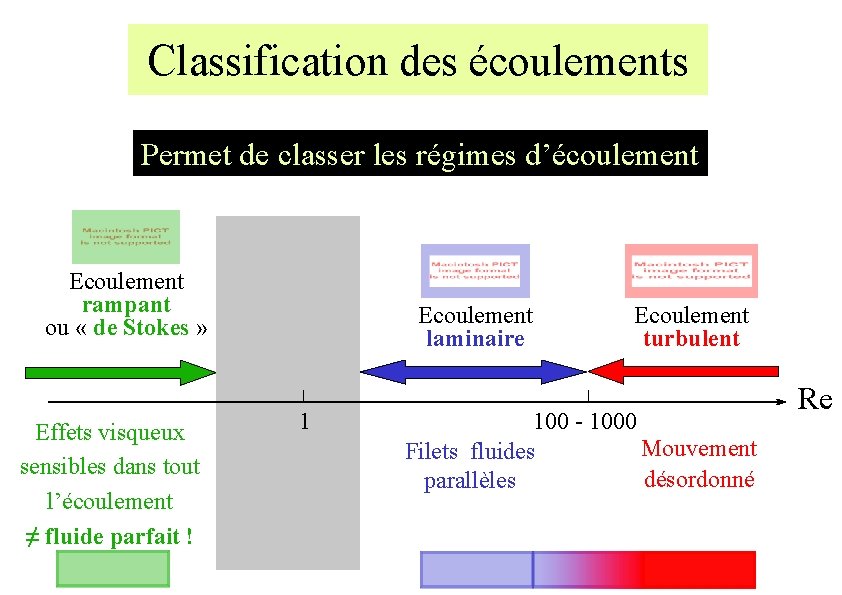
Classification des écoulements Permet de classer les régimes d’écoulement Ecoulement rampant ou « de Stokes » Effets visqueux sensibles dans tout l’écoulement ≠ fluide parfait ! Ecoulement laminaire 1 Ecoulement turbulent 100 - 1000 Mouvement Filets fluides désordonné parallèles Re

Ecoulement rampant (ou de Stokes) • Re << 1 (inertie négligeable devant frottements visqueux) • Effets visqueux sensibles dans tout l’écoulement • Equations linéaires => plusieurs solutions analytiques pratiques (suspensions, milieux poreux) • Réversible

Ecoulement rampant Re = 1, 5

Ecoulement laminaire Re = 26

Ecoulement laminaire

Transition laminaire-turbulent C’est Reynolds Expérience de Reynolds

Transition laminaire-turbulent Re = 200

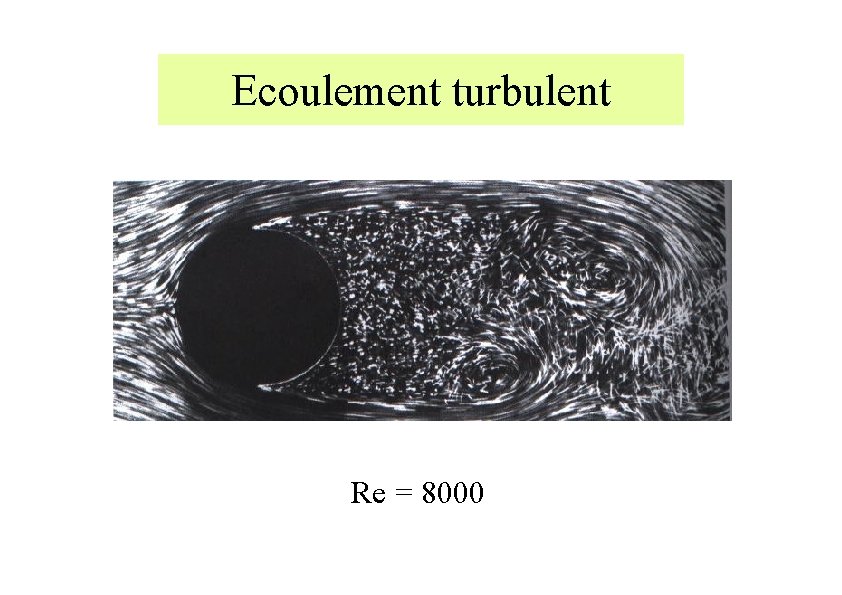
Ecoulement turbulent Re = 8000

Turbulence Déstabilisation de l’écoulement Ecoulement moyen + fluctuations de vitesse Fluctuations isotropes au coeur de l’écoulement Tourbillons d’échelles variées Transfert d’énergie des grandes échelles vers les petites La plus petite échelle (dite de « Kolmogorov » ) dissipe l’énergie Presque tous les écoulements industriels Les transferts massiques / thermiques sont plus efficaces Il existe des modèles numériques (k-e) utiles pour l’ingénieur MAIS reste encore un problème physique ouvert. . . ALORS QUE • échelle de l’homme • équations de la mécanique classique !

Turbulence « Je suis maintenant un vieil homme. Quand je mourrai, et irai au paradis, j’espère qu’on pourra m’éclairer sur 2 disciplines : l’électrodynamique quantique, et la turbulence des fluides. Pour la première, je suis plutôt optimiste. . . » Horace LAMB, physicien, 1932

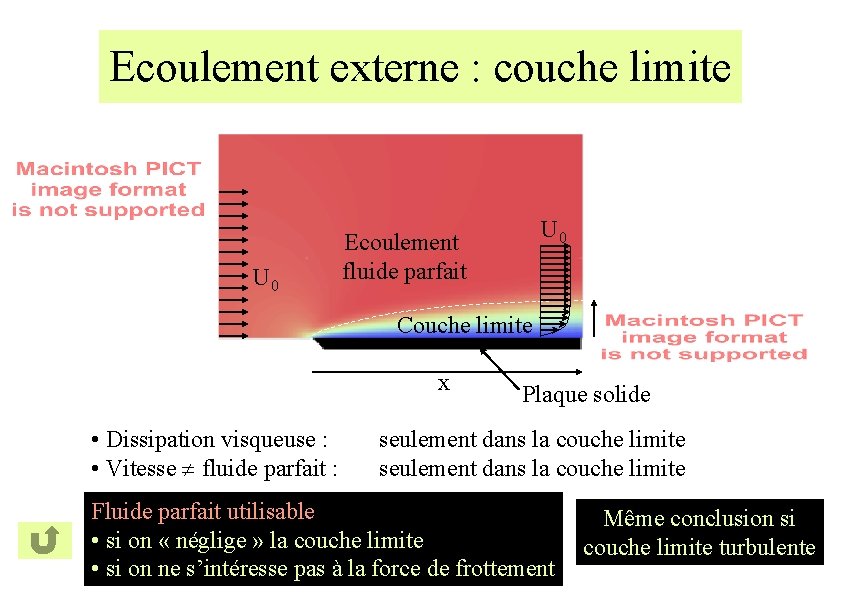
Ecoulement externe : couche limite U 0 Ecoulement fluide parfait Couche limite x • Dissipation visqueuse : • Vitesse fluide parfait : Plaque solide seulement dans la couche limite Fluide parfait utilisable • si on « néglige » la couche limite • si on ne s’intéresse pas à la force de frottement Même conclusion si couche limite turbulente

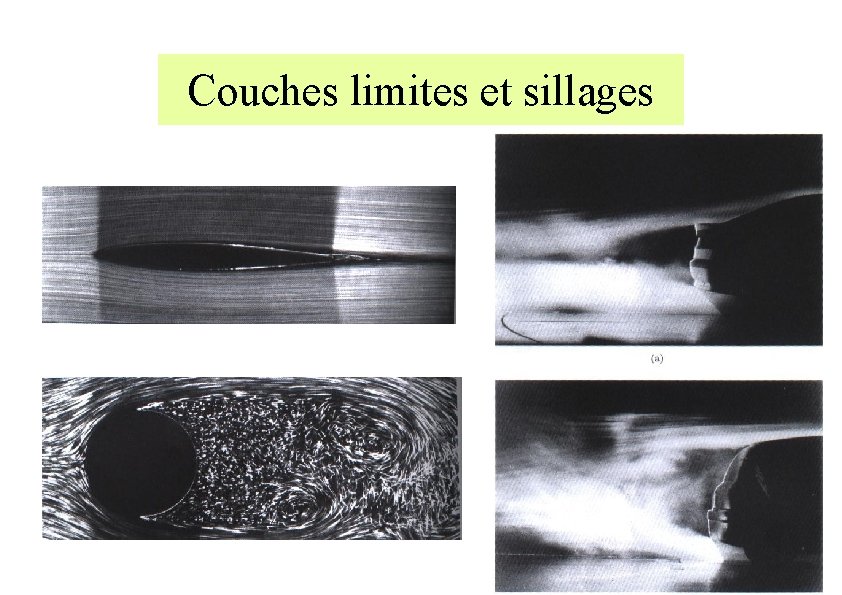
Couches limites et sillages

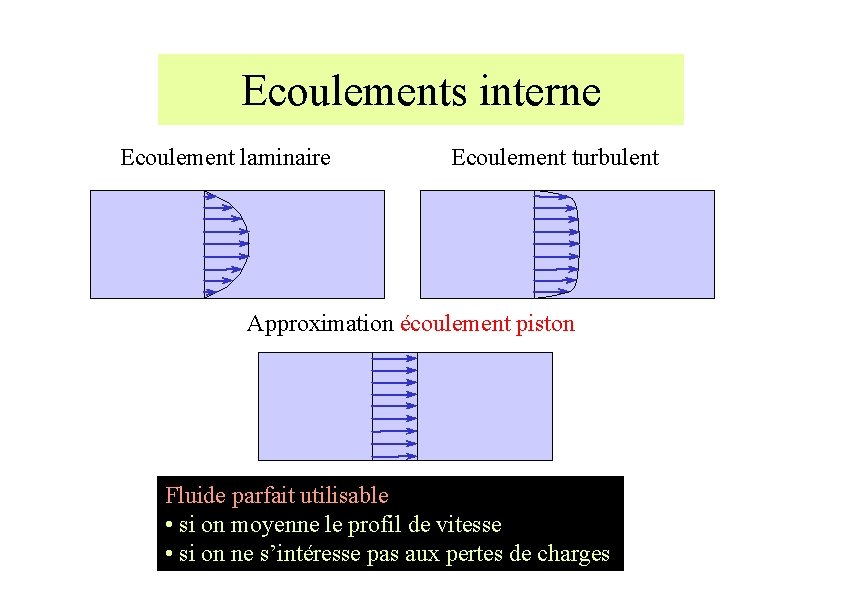
Ecoulements interne Ecoulement laminaire Ecoulement turbulent Approximation écoulement piston Fluide parfait utilisable • si on moyenne le profil de vitesse • si on ne s’intéresse pas aux pertes de charges

Validité fluide parfait • Ecoulements externes : Si Re >> 1, valable à l’extérieur de la couche limite (qui est petite) Mais ne rend pas compte de certains phénomènes (trainée) Si Re << 1, à traiter par théorie écoulements rampants • Ecoulements en conduite : Fluide parfait applicable (Bernoulli) pour tout Re Avec correction pour pertes de charges

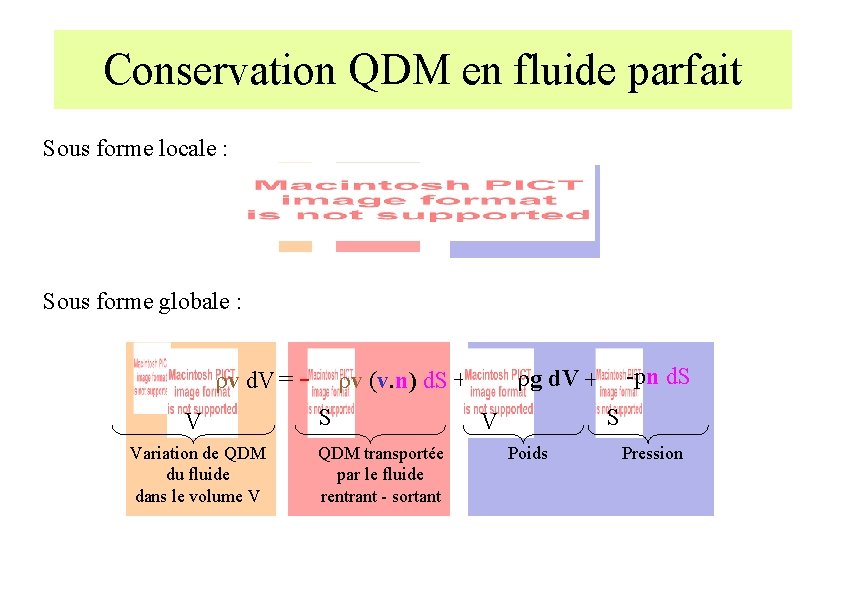
Conservation QDM en fluide parfait Sous forme locale : Sous forme globale : rv d. V = V Variation de QDM du fluide dans le volume V S QDM transportée par le fluide rentrant - sortant -pn d. S rg d. V + rv (v. n) d. S + S V Poids Pression

Fluide parfait incompressible r( x, y, z, t) = r 0 sv= 0 Equations locales : Masse QDM Une grande simplification est possible : Loi de Bernoulli

Conditions aux limites Quelles relations doit-on écrire aux frontières du domaines : • parois solides • interface avec autre fluide • entrée d’un écoulement (typiquement d’un tuyau) • sortie d’un écoulement (idem) • infiniment loin en amont d’un obstacle

Conditions aux limites • Paroi solide : normalement v = 0 ATTENTION : en fluide parfait, glissement autorisé on impose seulement : v. n = 0 n v • Sortie écoulement : p imposé (souvent = patm) et v // n • Infini amont : écoulement parallèle v = V 0

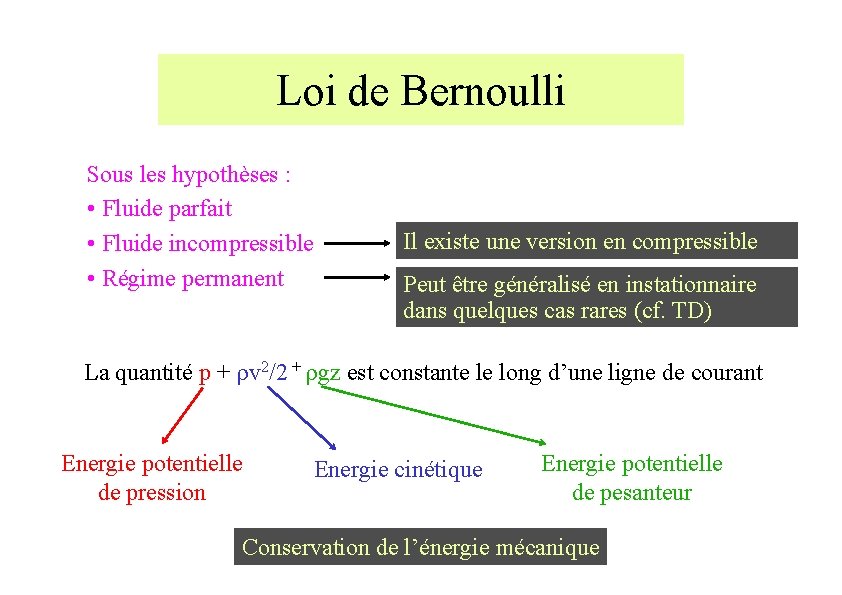
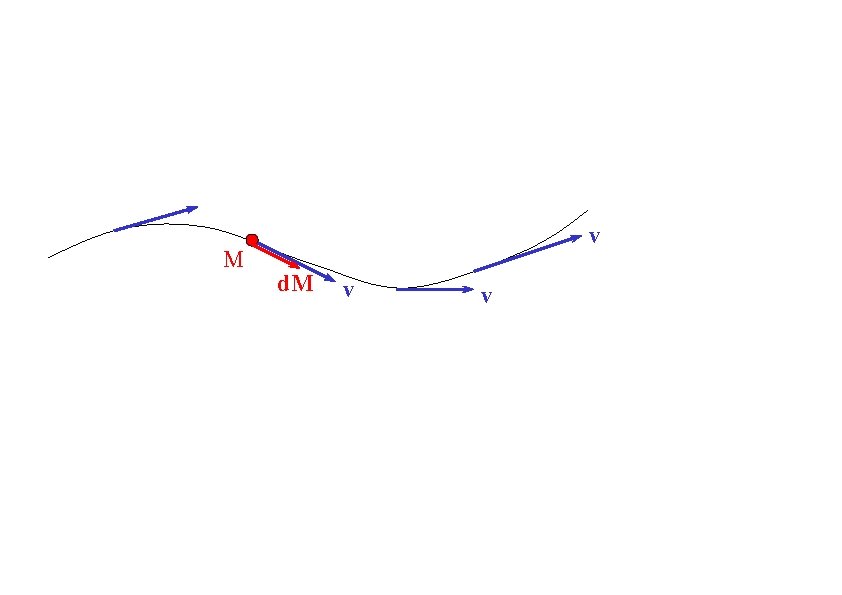
Loi de Bernoulli Ligne de courant : v // d. M v 1 M => (rot v v). d. M = (v d. M). rot v = 0 2 v d. M v v On suppose régime permanent => On projette la conservation QDM sur la ligne de courant r 0 ( grad v 2/2 + rot v v). d. M = (r 0 g - grad p). d. M De plus, on peut écrire g = grad (-gz) grad (r 0 v 2/2 + p + r 0 gz). d. M = 0 r 0 v 12/2 + p 1 + r 0 gz 1 = r 0 v 22/2 + p 2 + r 0 gz 2

Loi de Bernoulli Sous les hypothèses : • Fluide parfait • Fluide incompressible • Régime permanent Il existe une version en compressible Peut être généralisé en instationnaire dans quelques cas rares (cf. TD) La quantité p + rv 2/2 + rgz est constante le long d’une ligne de courant Energie potentielle de pression Energie cinétique Energie potentielle de pesanteur Conservation de l’énergie mécanique

Deuxième loi de Bernoulli Applicable aux écoulements irrotationnels rot v = 0 => v = grad f r 0 ( + grad v 2/2 + rot v v) = (r 0 g - grad p) De plus, on peut écrire g = grad (-gz) grad ( + r 0 v 2/2 + p + r 0 gz) = 0 dans tout l’écoulement ! On suppose régime permanent =>

M v d. M v v


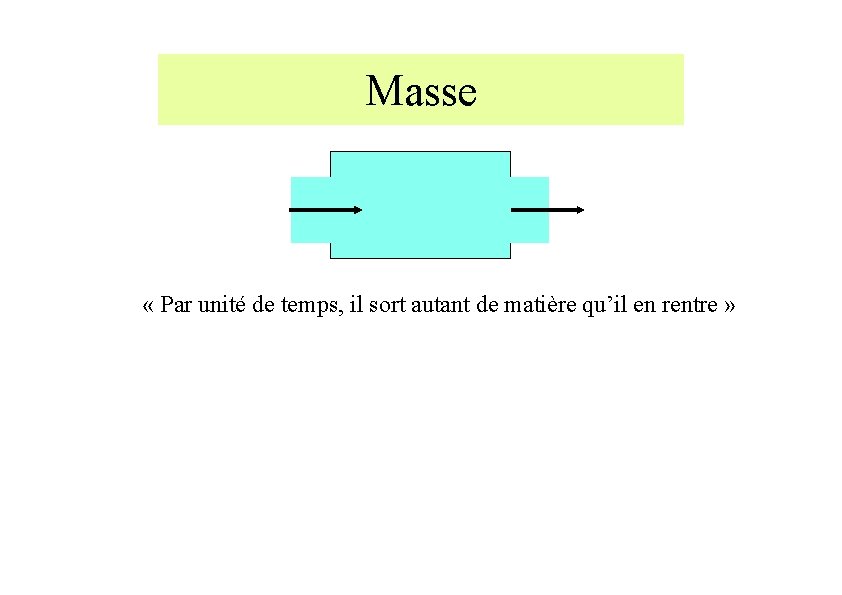
Masse « Par unité de temps, il sort autant de matière qu’il en rentre »
 écoulement rampant
écoulement rampant Olivier louisnard
Olivier louisnard Exercice glaçon dans verre d'eau
Exercice glaçon dans verre d'eau Simulation dynamique des fluides
Simulation dynamique des fluides Loi de refroidissement de newton
Loi de refroidissement de newton Mcanique
Mcanique Mcanique
Mcanique Bts fluides
Bts fluides Bts fluides
Bts fluides Des des des
Des des des Partie de campagne renoir
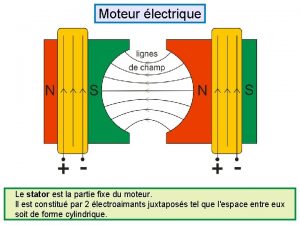
Partie de campagne renoir Partie fixe du moteur
Partie fixe du moteur Partie décimale
Partie décimale Figure de style boire un verre
Figure de style boire un verre Partie théorique et pratique
Partie théorique et pratique Tableau dixième centième
Tableau dixième centième Partie prenante management
Partie prenante management Où se trouve le centre de la terre
Où se trouve le centre de la terre Résumé la route de chlifa
Résumé la route de chlifa Organe ventre
Organe ventre Partie du corps du dauphin
Partie du corps du dauphin Fonction en escalier
Fonction en escalier System mrp przykład
System mrp przykład Partie de poisson
Partie de poisson Chimie partie 1
Chimie partie 1 Centroid engineering mechanics
Centroid engineering mechanics Difference between centre of gravity and centroid
Difference between centre of gravity and centroid Je t'offrirai des fleurs et des nappes en couleurs
Je t'offrirai des fleurs et des nappes en couleurs Le volume d'un corps
Le volume d'un corps Les modes verbaux et leurs valeurs
Les modes verbaux et leurs valeurs Robin des bois des alpes
Robin des bois des alpes Volume correspondant à une division
Volume correspondant à une division Triple des meet in the middle attack
Triple des meet in the middle attack La diffusion des idées des lumières
La diffusion des idées des lumières Affiche plan marshall ciment de l'europe
Affiche plan marshall ciment de l'europe Cartographie des flux de valeur
Cartographie des flux de valeur Budget des ventes méthode des moindres carrés
Budget des ventes méthode des moindres carrés Il existe des personnes qui sont des lumières pour tous
Il existe des personnes qui sont des lumières pour tous Diversification des espaces et des acteurs de la production
Diversification des espaces et des acteurs de la production Olivier duchemin
Olivier duchemin Dr casez
Dr casez Olivier milleron
Olivier milleron Besoekersboek gedig
Besoekersboek gedig Olivier sacroug
Olivier sacroug Olivier trecco
Olivier trecco Olivier arifon
Olivier arifon Julio olivier espiritismo
Julio olivier espiritismo Olivier ringoet
Olivier ringoet Fabrizio gagliardi
Fabrizio gagliardi Olivier dassault solidworks
Olivier dassault solidworks Olivier linaires
Olivier linaires Olivier senegas
Olivier senegas Olivier martin cern
Olivier martin cern Dustin hoffman laurence olivier
Dustin hoffman laurence olivier Mdd
Mdd Olivier tiffet
Olivier tiffet Source esi
Source esi Olivier caleff
Olivier caleff Olivier dusserre
Olivier dusserre Oliver de weck
Oliver de weck Olivier lortholary
Olivier lortholary Olivier callot
Olivier callot Olivier plichon
Olivier plichon Crtla
Crtla Dr mildred olivier
Dr mildred olivier Olivier michels
Olivier michels Olivier bouillanne
Olivier bouillanne Olivier sartre
Olivier sartre Olivier corten
Olivier corten Dagmar olivier
Dagmar olivier Irisnext
Irisnext Tlegend root cern
Tlegend root cern Analytical cubism characteristics
Analytical cubism characteristics Olivier lenglet
Olivier lenglet Olivier caleff
Olivier caleff Charles olivier bacri
Charles olivier bacri Olivier blanchard macroeconomia
Olivier blanchard macroeconomia Eps olivier
Eps olivier Feliz aniversario 10 años
Feliz aniversario 10 años Olivier elemento
Olivier elemento Olivier lenglet
Olivier lenglet Olivier thomann
Olivier thomann Olivier silla
Olivier silla Tristan olivier
Tristan olivier Olivier moindrot
Olivier moindrot