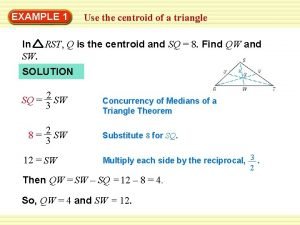
Centre of gravity and centroid Centre of gravity

Centre of gravity and centroid

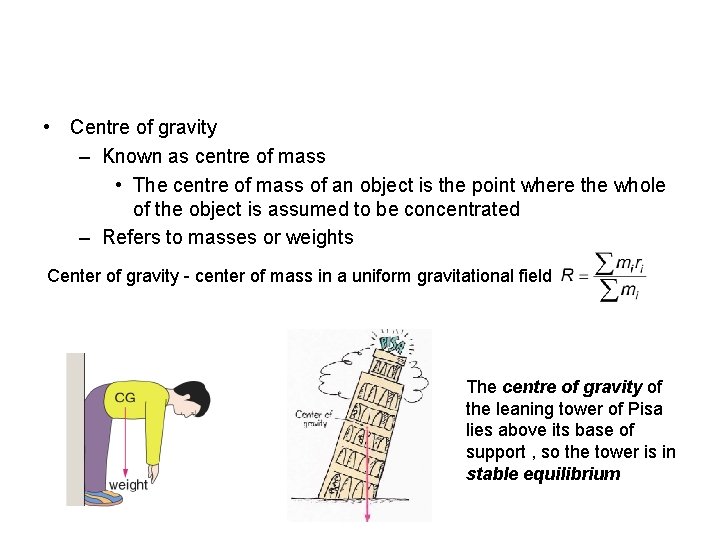
• Centre of gravity – Known as centre of mass • The centre of mass of an object is the point where the whole of the object is assumed to be concentrated – Refers to masses or weights Center of gravity - center of mass in a uniform gravitational field The centre of gravity of the leaning tower of Pisa lies above its base of support , so the tower is in stable equilibrium

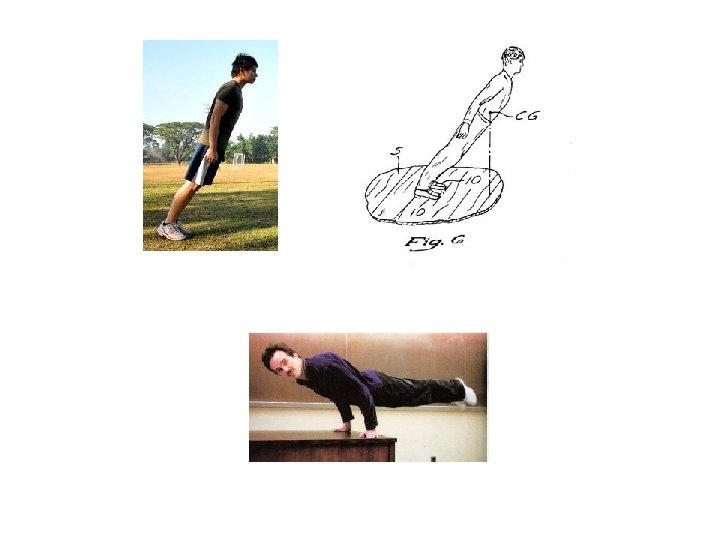
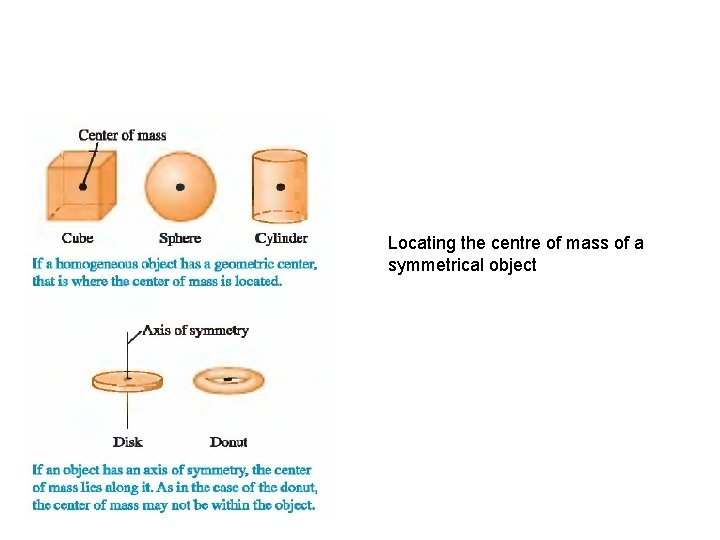
Locating the centre of mass of a symmetrical object

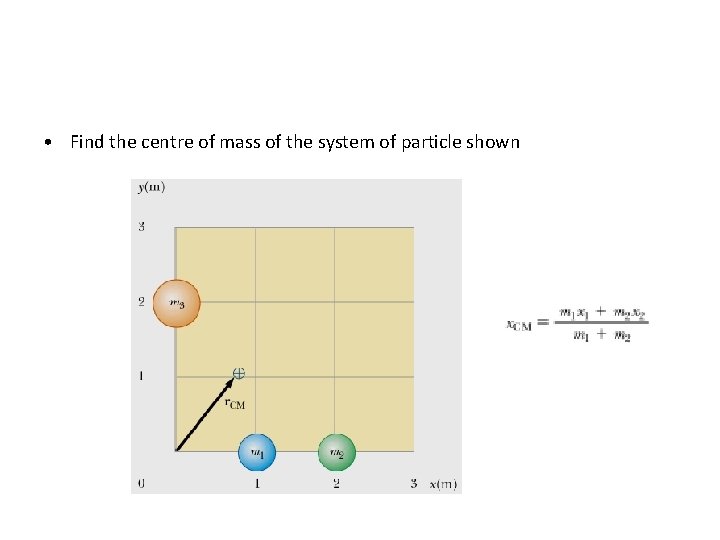
• Find the centre of mass of the system of particle shown

• Centroid – Ignoring weight and considering only volume – Different densities of material= the centre of gravity and centroid do not always coincide – Homogeneous = the centre of gravity and centroid would be coincide. – Type of centroid • Centroid of lines (rope. wire) • Centroid of areas (x, y) – Simple areas – Composite areas • Centroid of volume (x, y, z)

Centroid of line • for one-dimension object such as rope, wire and cable. • measured in length only. • the curve object, the centre of gravity is not located in the object and can be determined using formula of derivation. • the centroid can be determined by: The centroid of line whether straight, curve or composite lines can only be determined if the elements are connected and made up from a homogenous material. For the straight line, the centroid lies at a distance L/2 from reference axis. Normally, the centroid of line is always coincides with the center of gravity

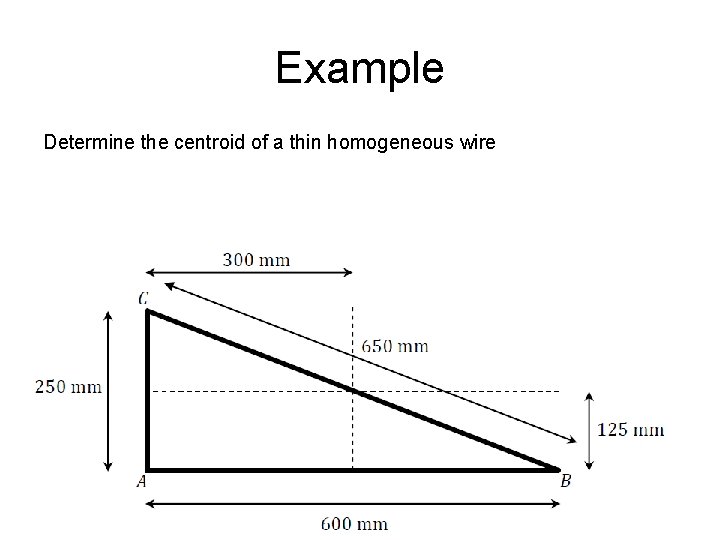
Example Determine the centroid of a thin homogeneous wire

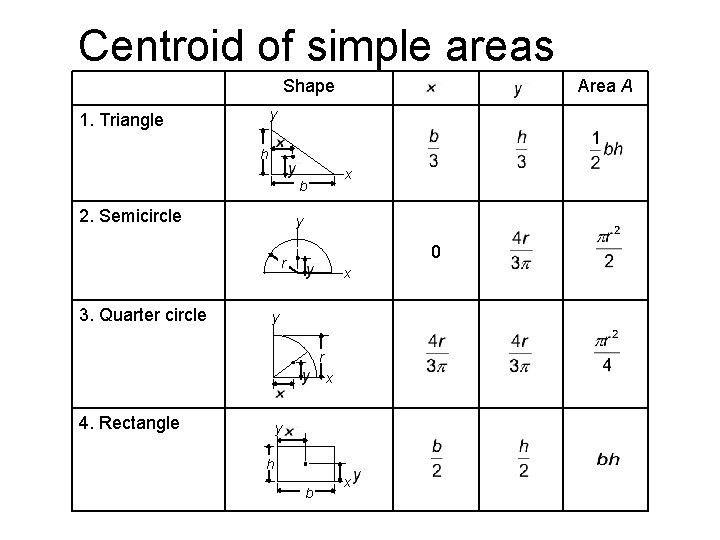
Centroid of simple areas Shape Area A y 1. Triangle h x b 2. Semicircle y 0 r 3. Quarter circle x y r x 4. Rectangle y h b x

Centroid of composite area • Composite areas are the combination of simple areas. • The determination of centroid is more easier if calculate in the table. 1 st Step: Divide the areas into several parts. 2 nd Step: State the reference axis in the figures. 3 rd Step: Find x 1, x 2 and y 1, y 2 from the reference axis that you stated. 4 th Step: Find the centroid. Ax = A 1 x 1 + A 2 x 2 Ay = A 1 y 1 + A 2 y 2 Total area, ΣA = A 1 + A 2

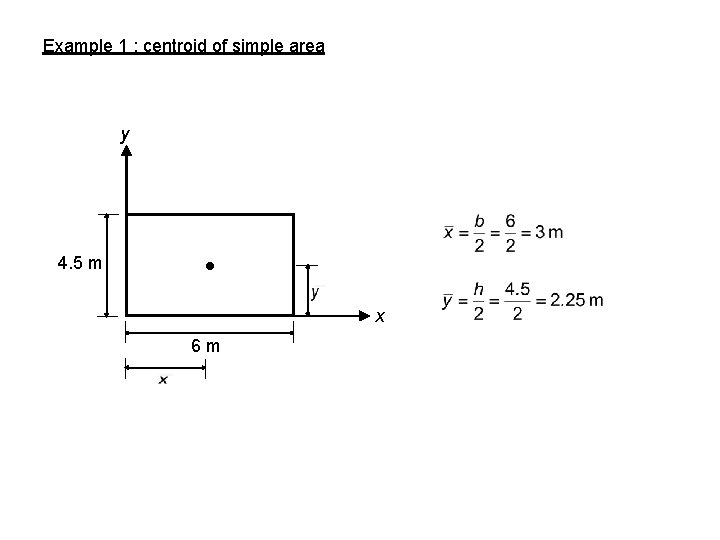
Example 1 : centroid of simple area y 4. 5 m x 6 m

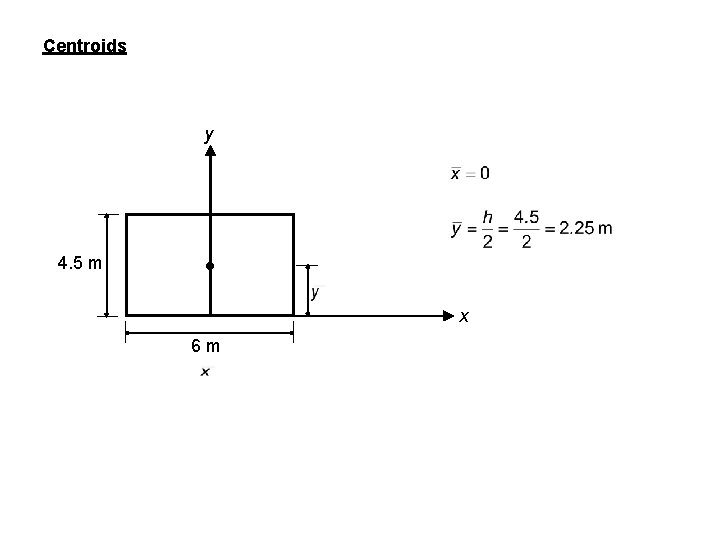
Centroids y 4. 5 m x 6 m

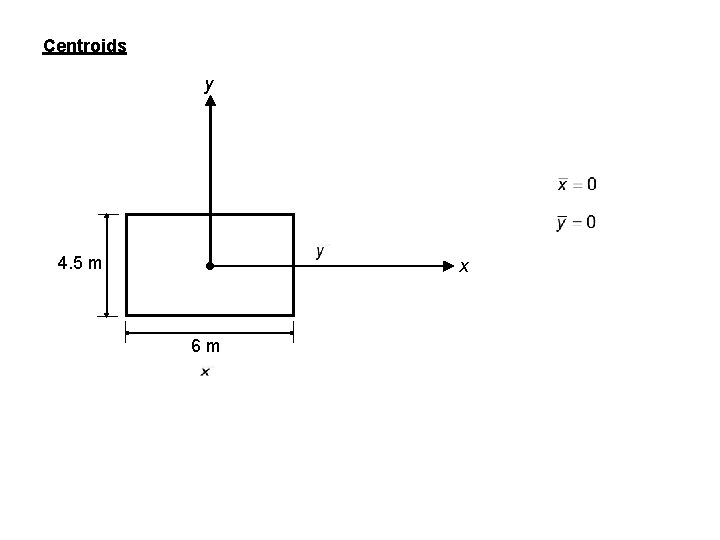
Centroids y 4. 5 m x 6 m

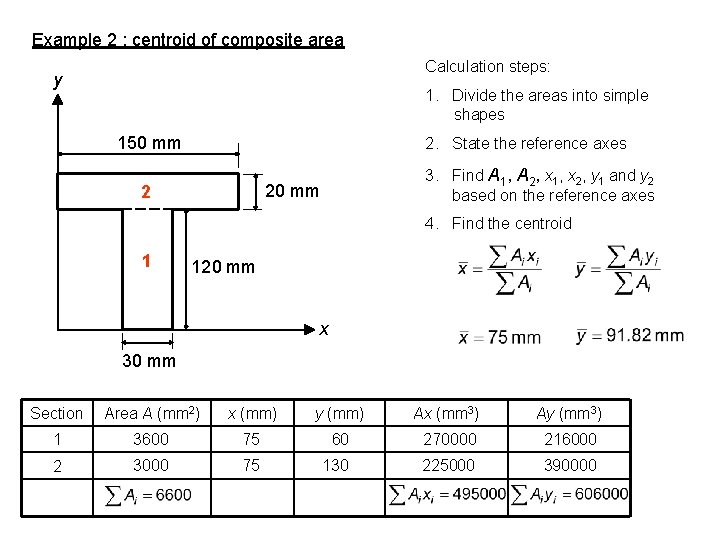
Example 2 : centroid of composite area Calculation steps: y 1. Divide the areas into simple shapes 150 mm 2. State the reference axes 3. Find A 1, A 2, x 1, x 2, y 1 and y 2 based on the reference axes 20 mm 2 4. Find the centroid 1 120 mm x 30 mm Section Area A (mm 2) x (mm) y (mm) Ax (mm 3) Ay (mm 3) 1 3600 75 60 270000 216000 2 3000 75 130 225000 390000

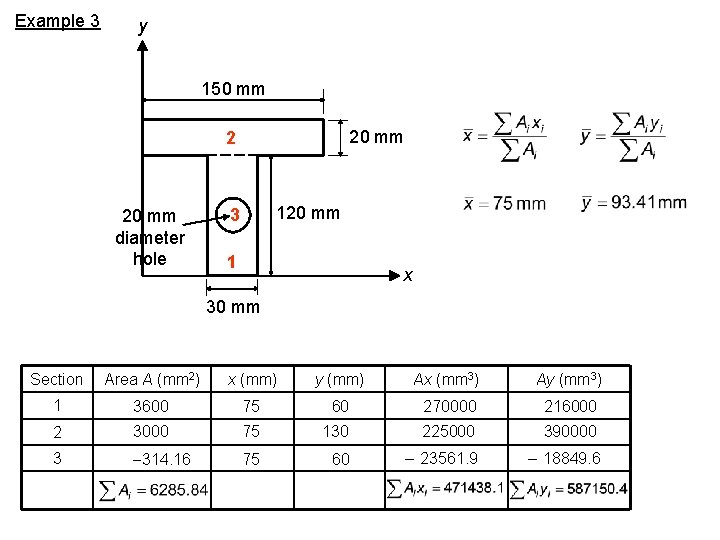
Example 3 y 150 mm 2 20 mm diameter hole 120 mm 3 1 x 30 mm Section Area A (mm 2) x (mm) y (mm) Ax (mm 3) Ay (mm 3) 1 3600 75 60 270000 216000 2 3000 75 130 225000 390000 3 314. 16 75 60 23561. 9 18849. 6

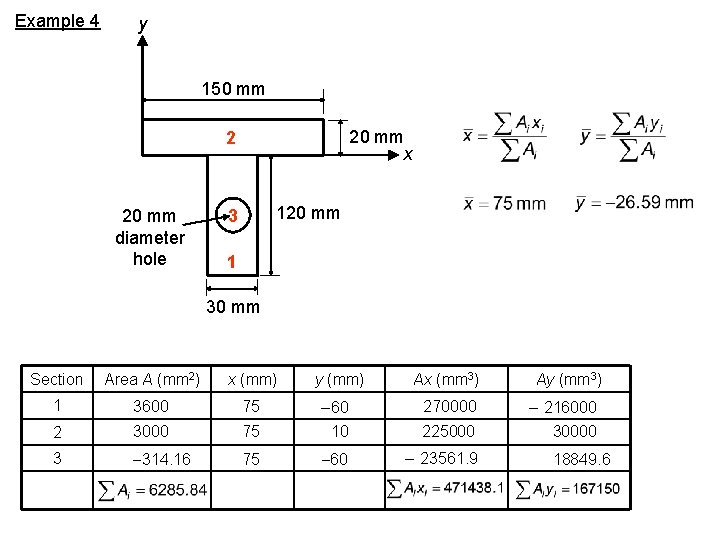
Example 4 y 150 mm 20 mm x 2 20 mm diameter hole 120 mm 3 1 30 mm Section Area A (mm 2) x (mm) y (mm) Ax (mm 3) Ay (mm 3) 1 3600 75 60 270000 216000 2 3000 75 10 225000 30000 3 314. 16 75 60 23561. 9 18849. 6

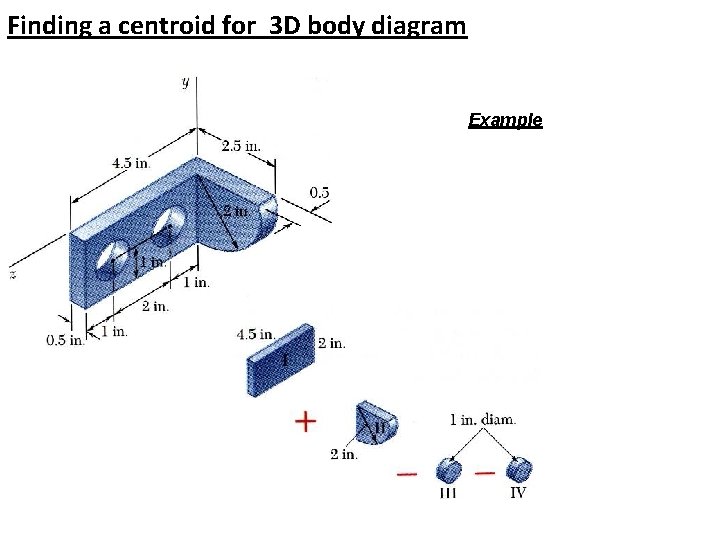
Finding a centroid for 3 D body diagram Example

Determine centre of mass or centre of gravity The difference between calculating the centroid using volume, mass, or weight is simply a scale factor, since mass and weight are proportional to volume as indicated below. (Greek letter rho) = mass density (typically expressed in kg/m 3 or slug/ft 3) m = V (Greek letter gamma) = weight density or specific weight (typically in N/m 3 or lb/ft 3) W = mg = g. V = V the centroids for mass and weight can be found as follows:

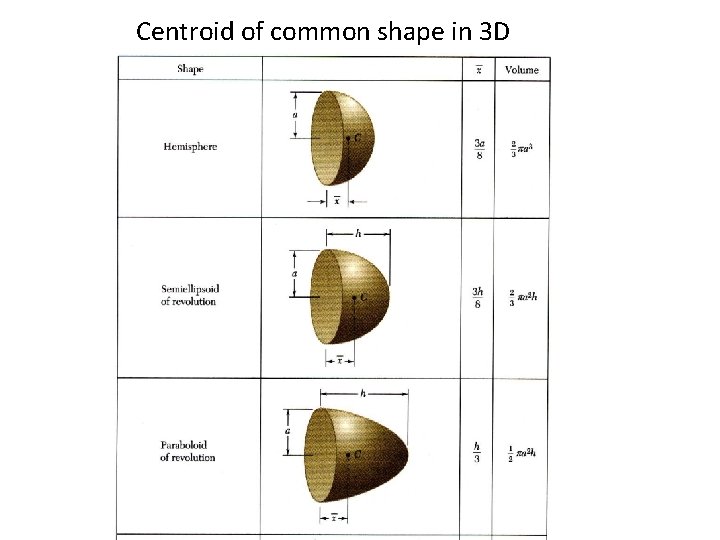
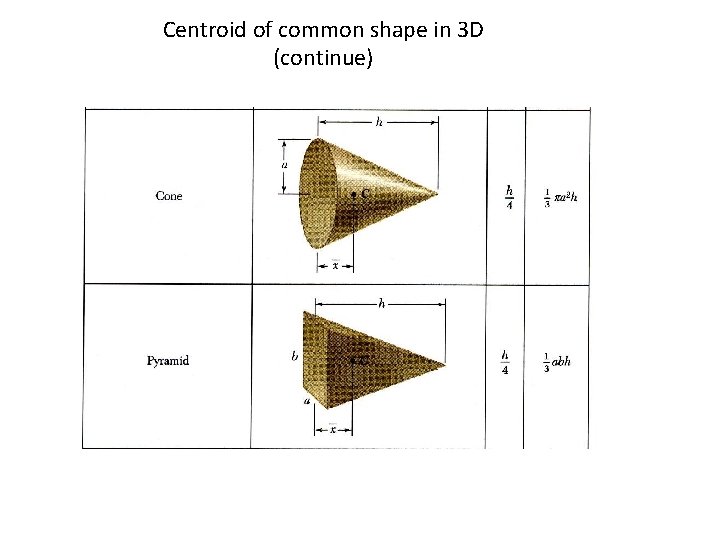
Centroid of common shape in 3 D

Centroid of common shape in 3 D (continue)

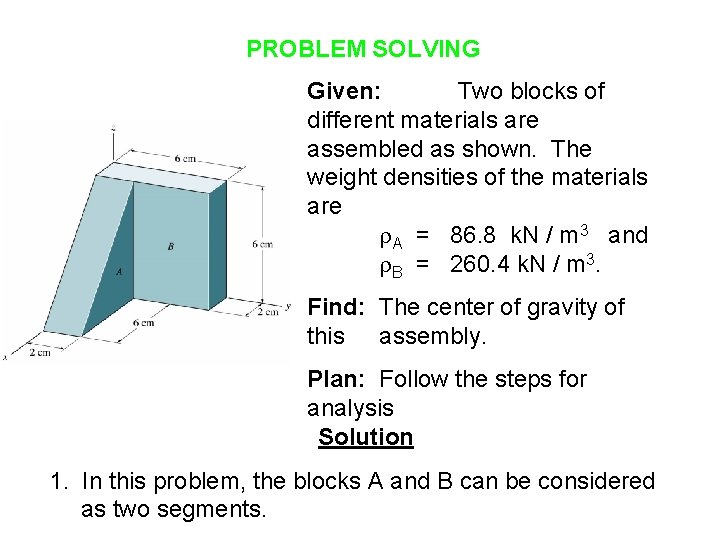
PROBLEM SOLVING Given: Two blocks of different materials are assembled as shown. The weight densities of the materials are A = 86. 8 k. N / m 3 and B = 260. 4 k. N / m 3. Find: The center of gravity of this assembly. Plan: Follow the steps for analysis Solution 1. In this problem, the blocks A and B can be considered as two segments.

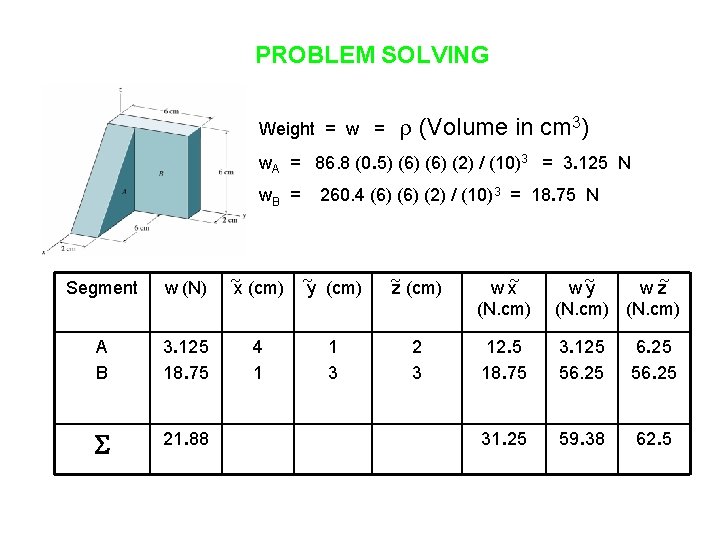
PROBLEM SOLVING Weight = w = (Volume in cm 3) w. A = 86. 8 (0. 5) (6) (2) / (10)3 = 3. 125 N w. B = 260. 4 (6) (2) / (10)3 = 18. 75 N Segment w (N) x (cm) y (cm) z (cm) w x (N. cm) w y w z (N. cm) A B 3. 125 18. 75 4 1 1 3 2 3 12. 5 18. 75 3. 125 56. 25 21. 88 31. 25 59. 38 62. 5

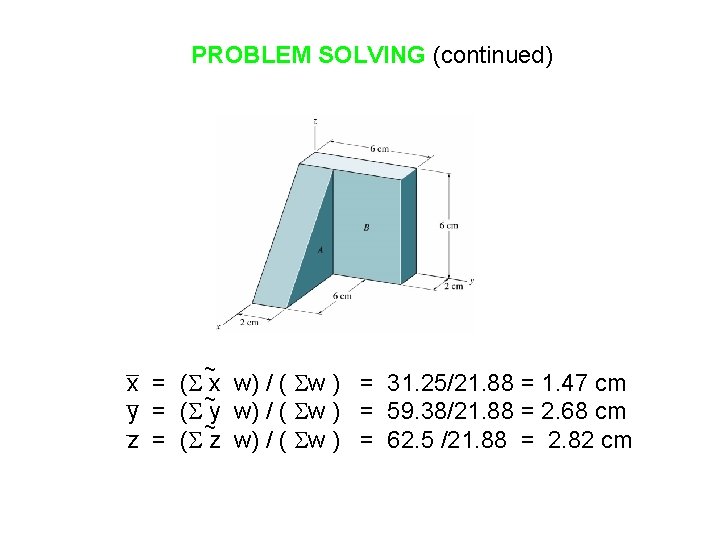
PROBLEM SOLVING (continued) ~ x = ( x w) / ( w ) = 31. 25/21. 88 = 1. 47 cm ~ y = ( y w) / ( w ) = 59. 38/21. 88 = 2. 68 cm ~ z = ( z w) / ( w ) = 62. 5 /21. 88 = 2. 82 cm

Application : Distributed load on Beam Illustration: The lumber on the rack shown below distributes the weight evenly across the supporting beam. This uniform loading is represented by a load curve with equal length lines. The total weight (resultant) equals the area under the load curve and it acts at the centroid of the load curve.

Application: Water tank To design the structure for supporting a water tank, we will need to know the weights of the tank and water as well as the locations where the resultant forces representing these distributed loads act. How can we determine these weights and their locations?

Application : Tilt-slab construction In tilt-slab construction, we have a concrete wall (with doors and windows cut out) which we need to raise into position. We don't want the wall to crack as we raise it, so we need to know the center of mass of the wall. How do we find the center of mass for such an uneven shape? Solution: 1. find the centroid of an area with straight sides 2. concept to areas with curved sides where we'll use integration.