Informatics and Mathematical Modelling Lars Kai Hansen Variational

Informatics and Mathematical Modelling / Lars Kai Hansen Variational Bayes 101 Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen The Bayes scene n Exact averaging in discrete/small models (Bayes networks) n Approximate averaging: - Monte Carlo methods - Ensemble/mean field - Variational Bayes methods Variational-Bayes. org MLpedia Wikipedia • ISP Bayes: ICA: mean field, Kalman, dynamical systems Neuro. Imaging: Optimal signal detector Approximate inference Machine learning methods Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Bayes’ methodology Minimal error rate obtained when detector is based on posterior probability (Bayes decision theory) Likelihood may contain unknown parameters Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Bayes’ methodology Conventional approach is to use most probable parameters However: averaged model is generalization optimal (Hansen, 1999), i. e. : Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen The hidden agenda of learning n Typically learning proceeds by generalization from limited set of samples…but n We would like to identify the model that generated the data n …. Choose the least complex model compatible with data Adv. Signal Proc. 2006 That I figured out in 1386

Informatics and Mathematical Modelling / Lars Kai Hansen Generalization! n Generalizability is defined as the expected performance on a random new sample. . . the mean performance of a model on a ”fresh” data set is an unbiased estimate of generalization n Typical loss functions: <-log p(x)> , < # prediction errors > < [ g(x)-ĝ(x) ] 2 >, <log p(x, g)/p(x)p(g)>, etc n Results can be presented as ”bias-variance trade-off curves” or ”learning curves” Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Generalization optimal predictive distribution n ”The game of guessing a pdf” n Assume: Random teacher drawn from P(θ), random data set, D, drawn from P(x|θ) n The prediction / generalization error is Predictive distribution of model A Adv. Signal Proc. 2006 Test sample distribution

Informatics and Mathematical Modelling / Lars Kai Hansen Generalization optimal predictive distribution We define the ”generalization functional” (Hansen, NIPS 1999) Minimized by the ”Bayesian averaging” predictive distribution Adv. Signal Proc. 2006

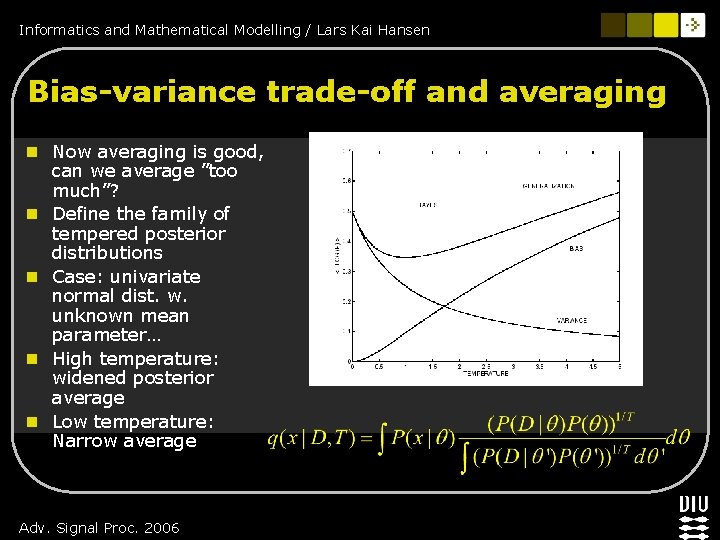
Informatics and Mathematical Modelling / Lars Kai Hansen Bias-variance trade-off and averaging n Now averaging is good, can we average ”too much”? n Define the family of tempered posterior distributions n Case: univariate normal dist. w. unknown mean parameter… n High temperature: widened posterior average n Low temperature: Narrow average Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Bayes’ model selection, example Let three models A, B, C be given n A) x is normal N(0, 1) n B) x is normal N(0, σ2), σ2 is uniform U(0, ∞) n C) x is normal N(μ, σ2), μ, σ2 are uniform U(0, ∞) Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Model A The likelihood of N samples is given by Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Model B The likelihood of N samples is given by Adv. Signal Proc. 2006

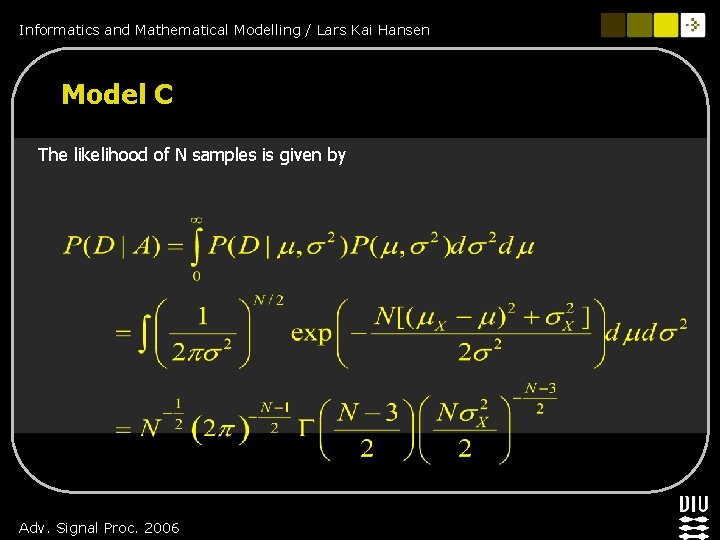
Informatics and Mathematical Modelling / Lars Kai Hansen Model C The likelihood of N samples is given by Adv. Signal Proc. 2006

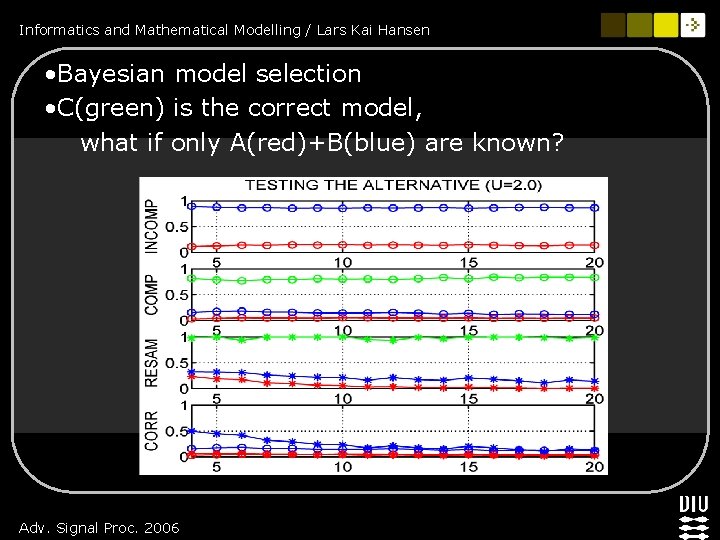
Informatics and Mathematical Modelling / Lars Kai Hansen • Bayesian model selection • C(green) is the correct model, what if only A(red)+B(blue) are known? Adv. Signal Proc. 2006

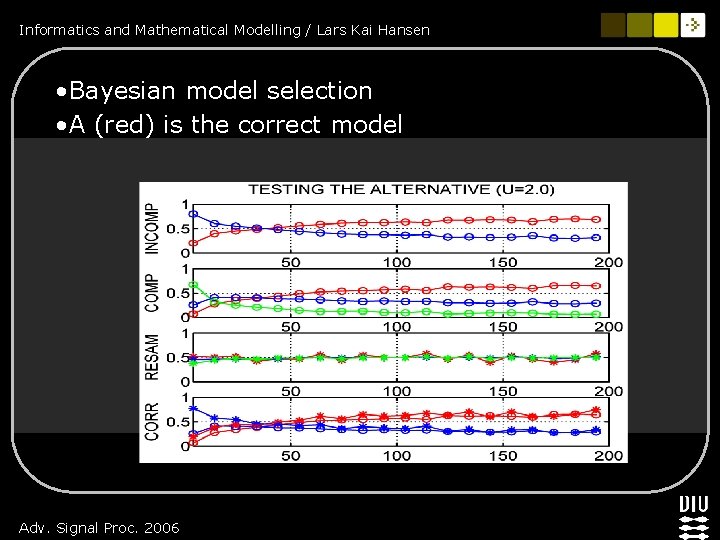
Informatics and Mathematical Modelling / Lars Kai Hansen • Bayesian model selection • A (red) is the correct model Adv. Signal Proc. 2006

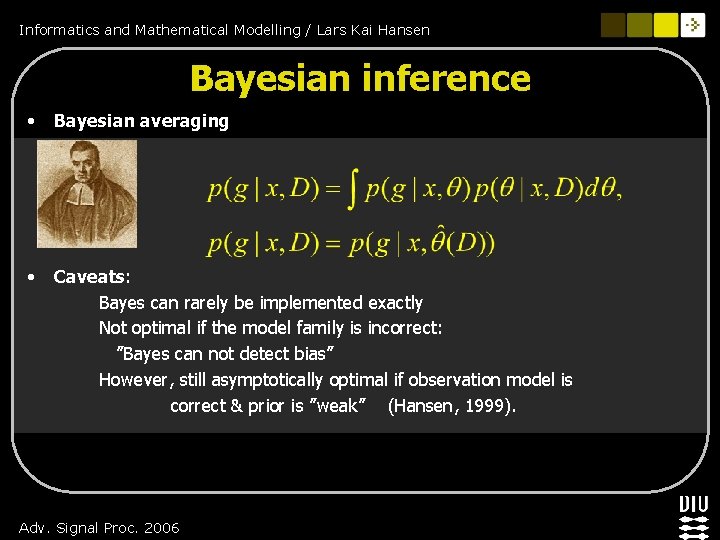
Informatics and Mathematical Modelling / Lars Kai Hansen Bayesian inference • Bayesian averaging • Caveats: Bayes can rarely be implemented exactly Not optimal if the model family is incorrect: ”Bayes can not detect bias” However, still asymptotically optimal if observation model is correct & prior is ”weak” (Hansen, 1999). Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Hierarchical Bayes models • Multi-level models in Bayesian averaging C. P. Robert: The Bayesian Choice - A Decision-Theoretic Motivation. Springer Texts in Statistics, Springer Verlag, New York (1994). G. Golub, M. Heath and G. Wahba, Generalized crossvalidation as a method for choosing a good ridge parameter, Technometrics 21 pp. 215– 223, (1979). K. Friston: A theory of Cortical Responses. Phil. Trans. R. Soc. B 360: 815 -836 (2005) Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Hierarchical Bayes models Posterior “learning hyper. Prior “Evidence” Target at Maximal evidence Adv. Signal Proc. 2006 parameters by adjusting prior expectations” -empirical Bayes -Mac. Kay, (1992) Hansen et al. (Eusipco, 2006) Cf. Boltzmann learning (Hinton et al. 1983)

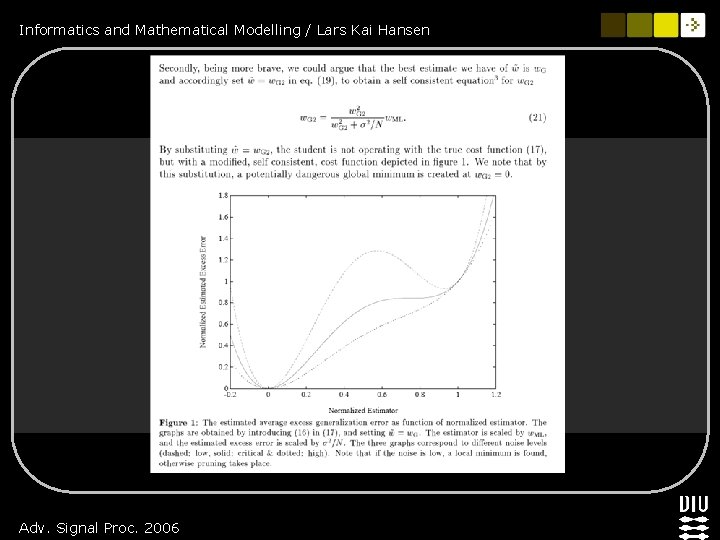
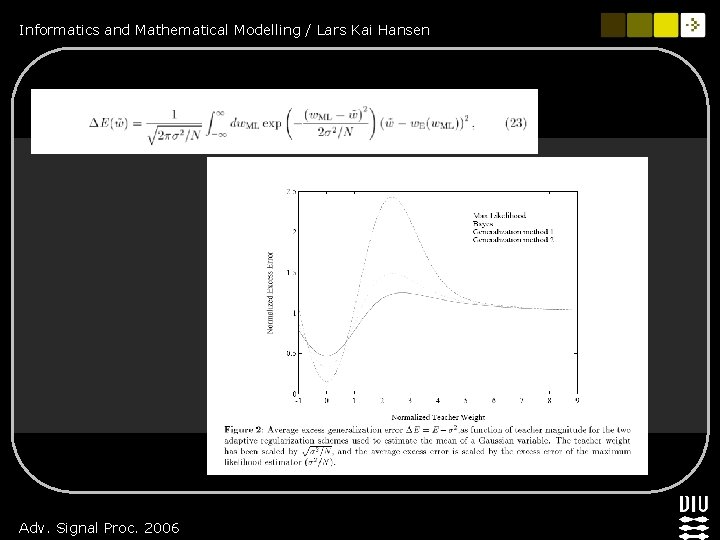
Informatics and Mathematical Modelling / Lars Kai Hansen Hyperparameter dynamics Gaussian prior w adaptive hyperparameter θ 2 A θML is a signal-to-noise measure is maximum lik. opt. Discontinuity: Parameter is pruned at Low signal-to-noise Hansen & Rasmussen, Neural Comp (1994) Tipping “Relevance vector machine” (1999) Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Hyperparameter dynamics n Hyperparameters dynamically updated implies pruning n Pruning decisions based on SNR n Mechanism for cognitive selection, attention? Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen & Rasmussen, Neural Comp (1994) Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

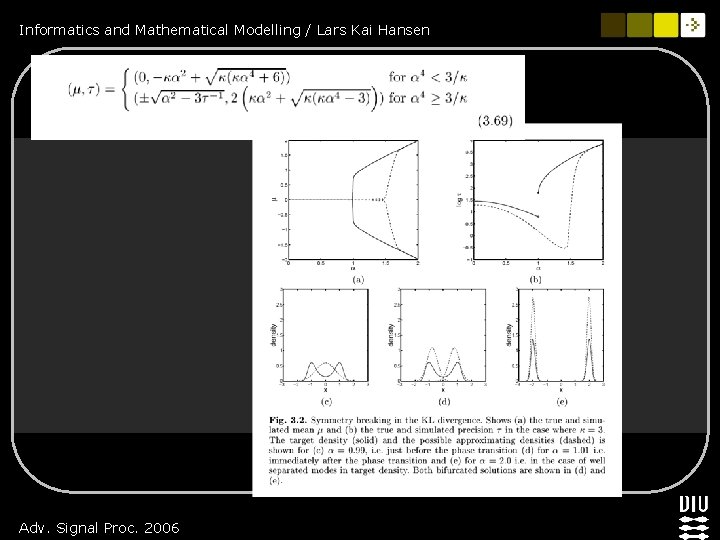
Informatics and Mathematical Modelling / Lars Kai Hansen Approximations needed for posteriors n Approximations using asymptotic expansions (Laplace etc) -JL n Approximation of posteriors using tractable (factorized) pdf’s by KL-fitting… n Approximation of products using EP -AH Wednesday n Approximation by MCMC –OWI Thursday Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Illustration of approximation by a gaussian pdf Adv. Signal Proc. 2006 P. Højen-Sørensen: Thesis (2001)

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Variational Bayes n Notation are observables and hidden variables n – we analyse the log likelihood of a mixture model Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Variational Bayes Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Variational Bayes: Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Conjugate exponential families Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Mini exercise n What are the natural parameters for a Gaussian? n What are the natural parameters for a Mo. G? Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen • Observation model and “Bayes factor” Adv. Signal Proc. 2006

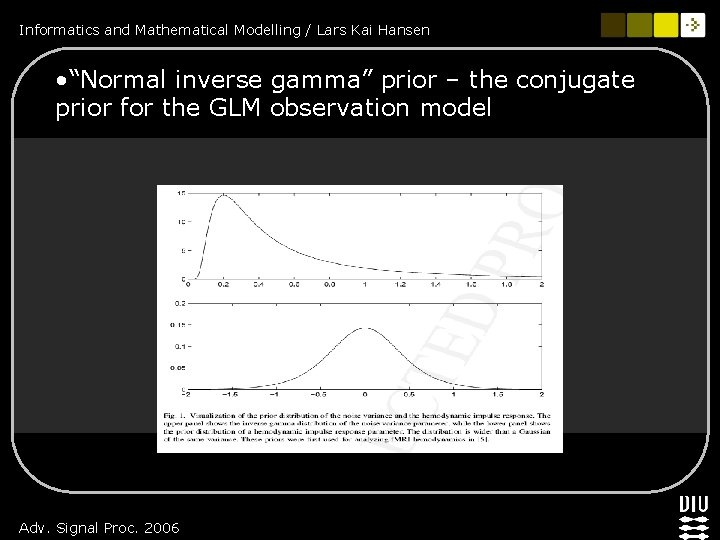
Informatics and Mathematical Modelling / Lars Kai Hansen • “Normal inverse gamma” prior – the conjugate prior for the GLM observation model Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen • “Normal inverse gamma” prior – the conjugate prior for the GLM observation model Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen • Bayes factor is the ratio between normalization const. of NIG’s: Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Adv. Signal Proc. 2006

Informatics and Mathematical Modelling / Lars Kai Hansen Exercises n Matthew Beal’s Mixture of Factor Analyzers code – Code available (variational-bayes. org) n Code a VB version of the BGML for signal detection – Code available for exact posterior Adv. Signal Proc. 2006