Mathematical background 1 Mathematical background Mathematical background 2

Mathematical background 1 Mathematical background

Mathematical background 2 Mathematics and engineering For engineers, mathematics is a tool: – Of course, that doesn’t mean it always works. . .

Mathematical background 3 Justification However, as engineers, you will not be paid to say: Method A is better than Method B or Algorithm A is faster than Algorithm B Such comparisons are said to be qualitative: qualitative, a. Relating to, connected or concerned with, quality or qualities. Now usually in implied or expressed opposition to quantitative.

Mathematical background 4 Justification Qualitative statements cannot guide engineering design decisions: – Algorithm A could be better than Algorithm B, but Algorithm A would require three person weeks to implement, test, and integrate while Algorithm B has already been implemented and has been used for the past year – There are circumstances where it may beneficial to use Algorithm A, but not based on the word better

Mathematical background 5 Justification Thus, we will look at a quantitative means of describing data structures and algorithms: quantitative, a. Relating to, concerned with, quantity or its measurement; ascertaining or expressing quantity. This will be based on mathematics, and therefore we will look at a number of properties which will be used again and again throughout this course

Mathematical background 6 Floor and ceiling functions The floor function maps any real number x onto the greatest integer less than or equal to x: – Consider it rounding towards negative infinity The ceiling function maps x onto the least integer greater than or equal to x: – Consider it rounding towards positive infinity

Mathematical background 7 Logarithms We will begin with a review of logarithms: If n = em, we define m = ln( n ) It is always true that eln(n) = n; however, ln(en) = n requires that n is real

Mathematical background 8 Logarithms Exponentials grow faster than any non-constant polynomial for any d > 0 Thus, their inverses—logarithms—grow slower than any polynomial
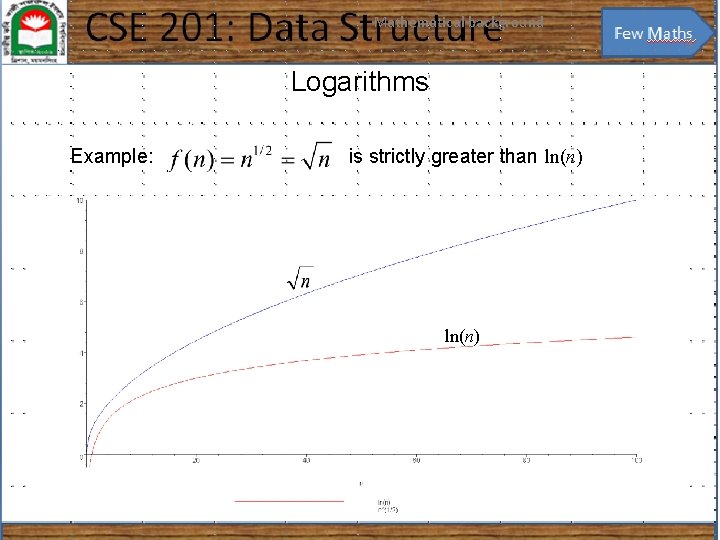
Mathematical background 9 Logarithms Example: is strictly greater than ln(n)
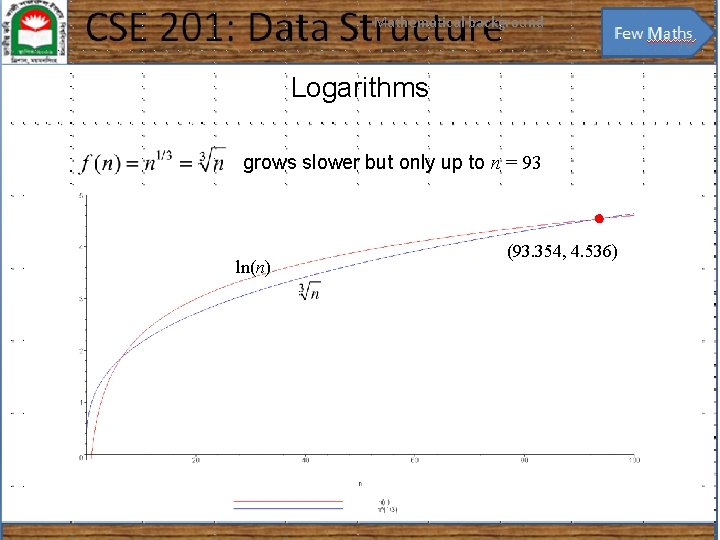
Mathematical background 10 Logarithms grows slower but only up to n = 93 ln(n) (93. 354, 4. 536)
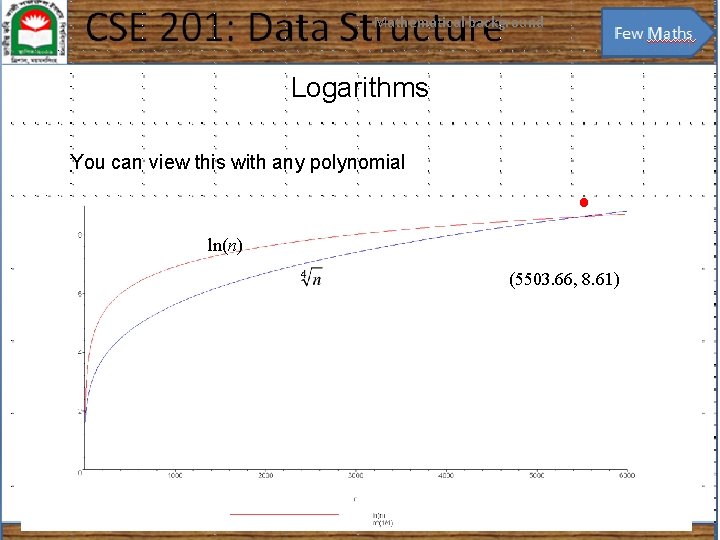
Mathematical background 11 Logarithms You can view this with any polynomial ln(n) (5503. 66, 8. 61)

Mathematical background 12 Logarithms We have compared logarithms and polynomials – How about log 2(n) versus ln(n) versus log 10(n) You have seen the formula Because, All logarithms are scalar multiples of each others Constant
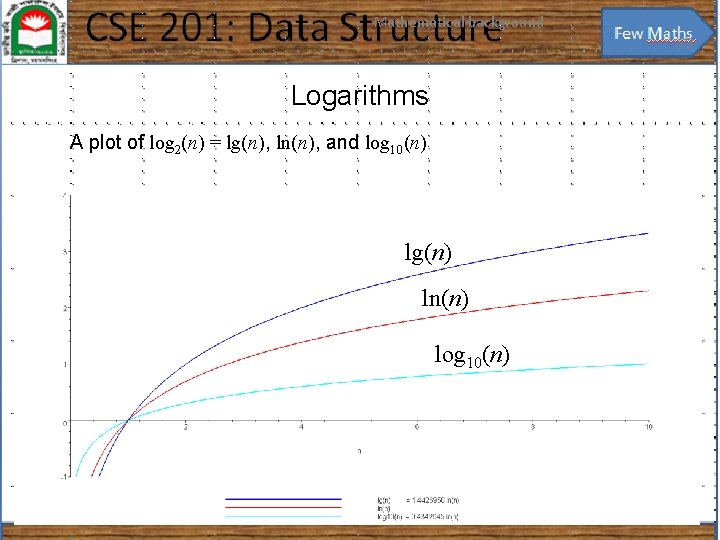
Mathematical background 13 Logarithms A plot of log 2(n) = lg(n), ln(n), and log 10(n) lg(n) ln(n) log 10(n)

Mathematical background 14 Logarithms You should also, as electrical or computer engineers be aware of the relationship: lg(210) = lg(1024) = 10 lg(220) = lg(1 048 576) = 20 and consequently: lg(103) = lg(1000) ≈ 10 kilo lg(106) = lg(1 000) ≈ 20 mega lg(109) ≈ 30 giga lg(1012) ≈ 40 tera

Mathematical background 15 Arithmetic series Next we will look various series Each term in an arithmetic series is increased by a constant value (usually 1) :

Mathematical background 16 Arithmetic series Proof 1: write out the series twice and add each column 1 + 2 + 3 +. . . + n – 2 + n – 1 + n – 2 +. . . + 3 + 2 + 1 (n + 1) +. . . + (n + 1) = n (n + 1) Since we added the series twice, we must divide the result by 2

Mathematical background 17 Arithmetic series Proof 2 (by induction): The statement is true for n = 0: Assume that the statement is true for an arbitrary n:

Mathematical background 18 Arithmetic series Using the assumption that for n, we must show that

Mathematical background 19 Arithmetic series Then, for n + 1, we have: By assumption, the second sum is known:

Mathematical background 20 Arithmetic series The statement is true for n = 0 and the truth of the statement for n implies the truth of the statement for n + 1. Therefore, by the process of mathematical induction, the statement is true for all values of n ≥ 0. Reference: Mr. Oprendick

Mathematical background 21 Other polynomial series We could repeat this process, after all: however, it is easier to see the pattern:
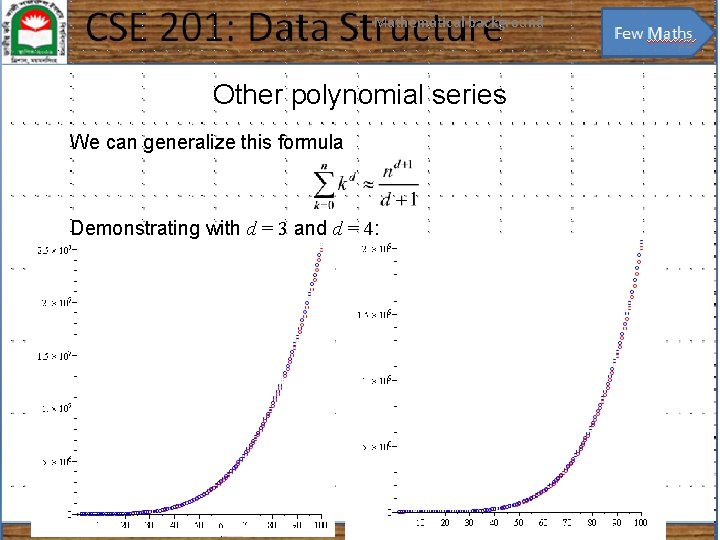
Mathematical background 22 Other polynomial series We can generalize this formula Demonstrating with d = 3 and d = 4:
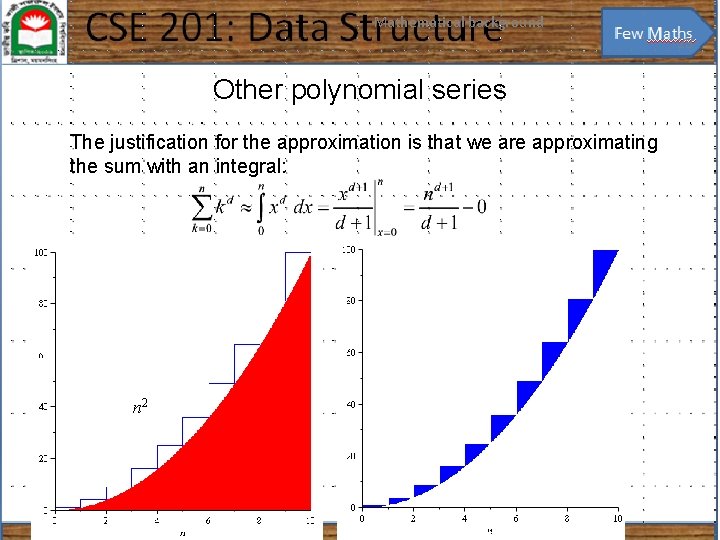
Mathematical background 23 Other polynomial series The justification for the approximation is that we are approximating the sum with an integral: n 2

Mathematical background 24 Other polynomial series The ratio between the error and the actual value goes to zero: – In the limit, as n → ∞, the ratio between the sum and the approximation goes to 1 – The relative error of the approximation goes to 0

Mathematical background 25 Geometric series The next series we will look at is the geometric series with common ratio r: and if |r| < 1 then it is also true that
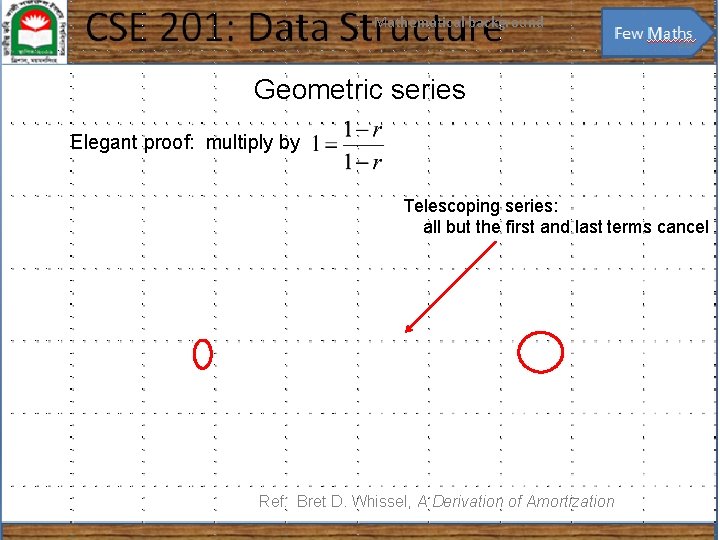
Mathematical background 26 Geometric series Elegant proof: multiply by Telescoping series: all but the first and last terms cancel Ref: Bret D. Whissel, A Derivation of Amortization

Mathematical background 27 Geometric series Note that we can use a change-of-index with summations like we do with integration: Letting j = i – 1:

Mathematical background 28 Recurrence relations Finally, we will review recurrence relations: – Sequences may be defined explicitly: xn = 1/n 1, 1/2, 1/3, 1/4, . . . Here n is xn independent. – Consider a fibonacci series where F 1=1, F 2=2 and F=F+F Then the series is 1, 2, 3, 5, 8, 13, 21, … – A recurrence relationship is a means of defining a sequence based on previous values in the sequence – Such definitions of sequences are said to be recursive

Mathematical background 29 Recurrence relations Define an initial value: e. g. , x 1 = 1 Defining xn in terms of previous values: – For example, xn = x n – 1 + 2 xn = 2 xn – 1 + n xn = xn – 1 + xn – 2

Mathematical background 30 Recurrence relations Given the two recurrence relations xn = x n – 1 + 2 xn = 2 xn – 1 + n and the initial condition x 1 = 1 we would like to find explicit formulae for the sequences In this case, we have xn = 2 n – 1 respectively xn = 2 n + 1 – n – 2

Mathematical background 31 Recurrence relations We will use a functional form of recurrence relations: Calculus CSE x 1 = 1. . . f(1) = 1. . . . . xn = xn – 1 + 2. . f(n) = f(n – 1) + 2. . . xn = 2 xn – 1 + n f(n) = 2 f(n – 1) + n

Mathematical background 32 Recurrence relations The previous examples using the functional notation are: f(n) = f(n – 1) + 2 g(n) = 2 g(n – 1) + n With the initial conditions f(1) = g(1) = 1, the solutions are: f(n) = 2 n – 1 g(n) = 2 n + 1 – n – 2

Mathematical background 33 Recurrence relations In some cases, given the recurrence relation, we can find the explicit formula: – Consider the Fibonacci sequence: f(n) = f(n – 1) + f(n – 2) f(0) = f(1) = 1 that has the solution where f is the golden ratio:

Mathematical background 34 Weighted averages Given n objects x 1, x 2, x 3, . . . , xn, the average is Given a sequence of coefficients c 1 , c 2 , c 3 , … , cn where then we refer to as a weighted average For an average,

Mathematical background 35 Weighted averages Examples: – Simpson’s method approximates an integral by sampling the function at three points: f(a), f(b), f(c) – The average value of the function is approximated by – It can be shown that is a significant better approximation than

Mathematical background 36 Weighted averages Examples: – Using the weighted average: – Using a simple average:

Mathematical background 37 Combinations Given n distinct items, in how many ways can you choose k of these? – I. e. , “In how many ways can you combine k items from n? ” – For example, given the set {1, 2, 3, 4, 5}, I can choose three of these in any of the following ways: {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}, The number of ways such items can be chosen is written where is read as “n choose k”s There is a recursive definition:

Mathematical background 38 Combinations The most common question we will ask in this vein: – Given n items, in how many ways can we choose two of them? – In this case, the formula simplifies to: For example, given {0, 1, 2, 3, 4, 5, 6}, we have the following 21 pairs: {0, 1}, {0, 2}, {0, 3}, {0, 4}, {0, 5}, {0, 6}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}, {4, 5}, {4, 6}, {5, 6}

Mathematical background 39 Combinations You have also seen this in expanding polynomials: For example,

Mathematical background 40 Combinations These are also the coefficients of Pascal’s triangle:

Mathematical background 41 Absolute Value or Modulus of a |a|= non-negative value of a Example: |5|=5 |0|=0 |-5|=5 |-5. 5|=5. 5

Mathematical background 42 Modulo the result of the modulo operation is the remainder of the Euclidean division. In nearly all computing systems, the quotient q and the remainder r of a divided by n satisfy q is an integer number. a=nq+r |r|<|n| This is then written as r=(a mod n)
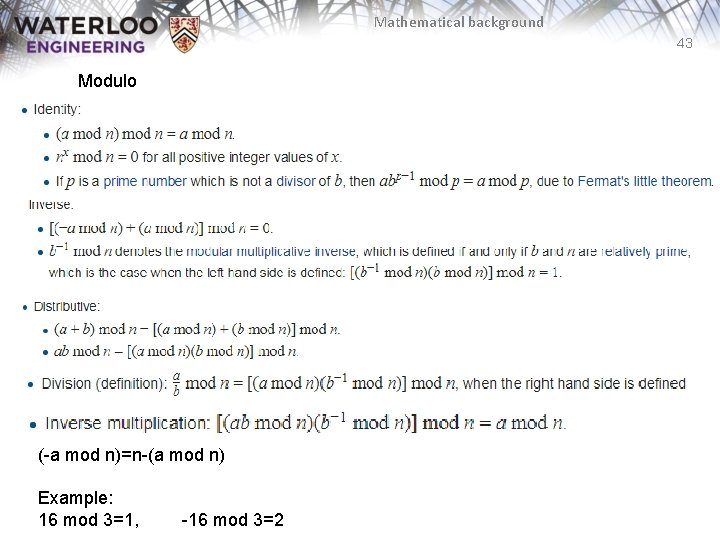
Mathematical background 43 Modulo (-a mod n)=n-(a mod n) Example: 16 mod 3=1, -16 mod 3=2

Mathematical background 44 End of the Chapter
- Slides: 44