Informatics and Mathematical Modelling Intelligent Signal Processing Nonnegative

Informatics and Mathematical Modelling / Intelligent Signal Processing Non-negative Tensor Decompositions Morten Mørup Informatics and Mathematical Modeling Intelligent Signal Processing Technical University of Denmark Morten Mørup 1

Informatics and Mathematical Modelling / Intelligent Signal Processing Sæby, May 22 -2006 Parts of the work done in collaboration with Lars Kai Hansen, Professor Department of Signal Processing Informatics and Mathematical Modeling, Technical University of Denmark Morten Mørup Sidse M. Arnfred, Dr. Med. Ph. D Mikkel N. Schmidt, Stud. Ph. D Cognitive Research Unit Hvidovre Hospital University Hospital of Copenhagen Department of Signal Processing Informatics and Mathematical Modeling, Technical University of Denmark 2

Informatics and Mathematical Modelling / Intelligent Signal Processing Overview n Non-negativity Matrix Factorization (NMF) n Sparse coding NMF (SNMF) n Sparse Higher Order Non-negative Matrix Factorization (HONMF) n Sparse Non-negative Tensor double deconvolution (SNTF 2 D) Morten Mørup 3

Informatics and Mathematical Modelling / Intelligent Signal Processing Factor Analysis d V WH Int. tests Subjects Int. Spearman ~1900 Vtests x subjects Wtests x intelligences. Hintelligencesxsubject Non-negative Matrix Factorization (NMF): V WH s. t. Wi, d, Hd, j 0 (~1970 Lawson, ~1995 Paatero, ~2000 Lee & Seung) Morten Mørup 4

Informatics and Mathematical Modelling / Intelligent Signal Processing The idea behind multiplicative updates Positive term Morten Mørup 5 Negative term

Informatics and Mathematical Modelling / Intelligent Signal Processing Non-negative matrix factorization (NMF) (Lee & Seung - 2001) NMF gives Part based representation (Lee & Seung – Nature 1999) Morten Mørup 6

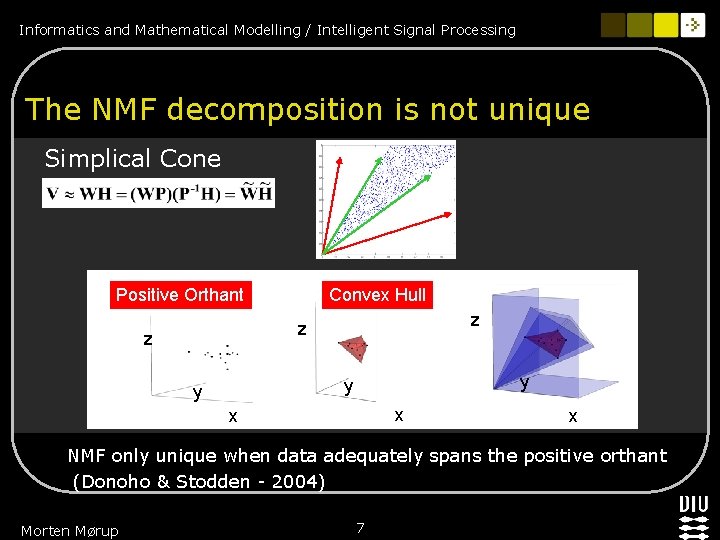
Informatics and Mathematical Modelling / Intelligent Signal Processing The NMF decomposition is not unique Simplical Cone Positive Orthant Convex Hull z z z y y y x x x NMF only unique when data adequately spans the positive orthant (Donoho & Stodden - 2004) Morten Mørup 7

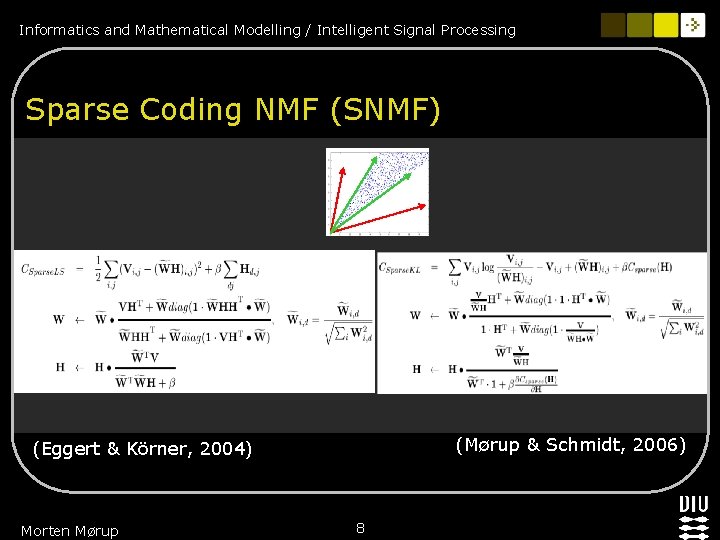
Informatics and Mathematical Modelling / Intelligent Signal Processing Sparse Coding NMF (SNMF) (Mørup & Schmidt, 2006) (Eggert & Körner, 2004) Morten Mørup 8

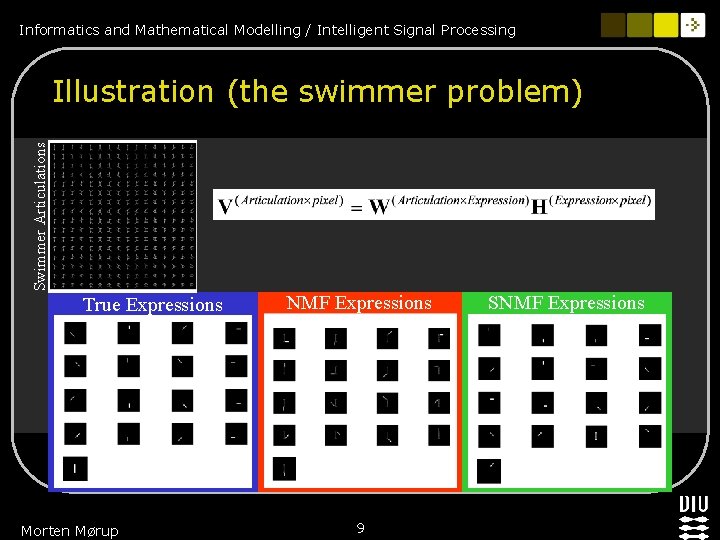
Informatics and Mathematical Modelling / Intelligent Signal Processing Swimmer Articulations Illustration (the swimmer problem) True Expressions Morten Mørup NMF Expressions 9 SNMF Expressions

Informatics and Mathematical Modelling / Intelligent Signal Processing Why sparseness? n Ensures uniqueness n Eases interpretability (sparse representation factor effects pertain to fewer dimensions) n Can work as model selection (Sparseness can turn off excess factors by letting them become zero) n Resolves over complete representations (when model has many more free variables than data points) Morten Mørup 10

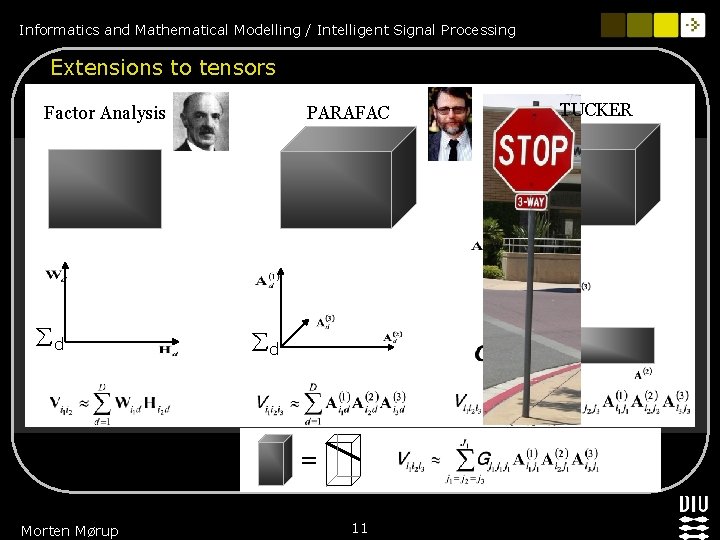
Informatics and Mathematical Modelling / Intelligent Signal Processing Extensions to tensors Factor Analysis d PARAFAC d = Morten Mørup 11 TUCKER

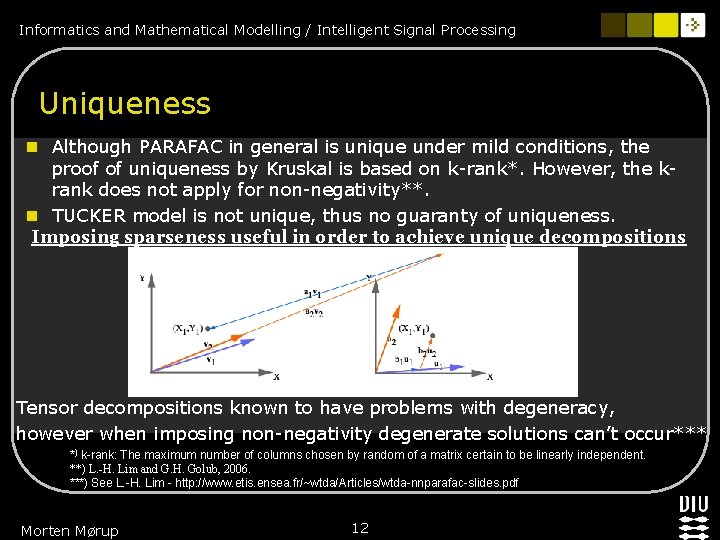
Informatics and Mathematical Modelling / Intelligent Signal Processing Uniqueness n Although PARAFAC in general is unique under mild conditions, the proof of uniqueness by Kruskal is based on k-rank*. However, the krank does not apply for non-negativity**. n TUCKER model is not unique, thus no guaranty of uniqueness. Imposing sparseness useful in order to achieve unique decompositions Tensor decompositions known to have problems with degeneracy, however when imposing non-negativity degenerate solutions can’t occur*** *) k-rank: The maximum number of columns chosen by random of a matrix certain to be linearly independent. **) L. -H. Lim and G. H. Golub, 2006. ***) See L. -H. Lim - http: //www. etis. ensea. fr/~wtda/Articles/wtda-nnparafac-slides. pdf Morten Mørup 12

Informatics and Mathematical Modelling / Intelligent Signal Processing Example why Non-negative PARAFAC isn’t unique Morten Mørup 13

Informatics and Mathematical Modelling / Intelligent Signal Processing PARAFAC model estimation d Thus, the PARAFAC model is by the matricizing operation estimated straight forward from regular NMF estimation by interchanging W with A and H with Z. Morten Mørup 14

Informatics and Mathematical Modelling / Intelligent Signal Processing TUCKER model estimation TUCKER Morten Mørup 15

Informatics and Mathematical Modelling / Intelligent Signal Processing Algorithms for Non-negative TUCKER (PARAFAC follows by setting C=I) (Mørup et al. 2006) Morten Mørup 16

Informatics and Mathematical Modelling / Intelligent Signal Processing Application of Non-negative TUCKER and PARAFAC Non-negative TUCKER in the following called HONMF (Higher order non-negative matrix factorization) Non-negative PARAFAC called NTF (Non-negative tensor factorization) Morten Mørup 17

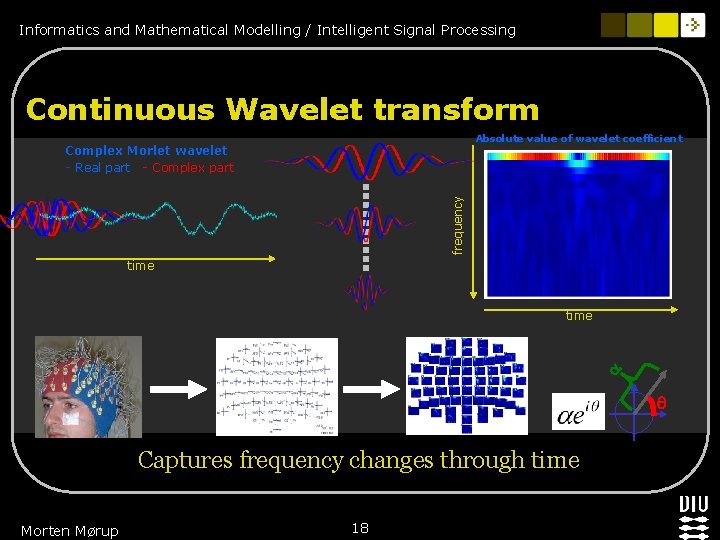
Informatics and Mathematical Modelling / Intelligent Signal Processing Continuous Wavelet transform Absolute value of wavelet coefficient frequency Complex Morlet wavelet - Real part - Complex part time Captures frequency changes through time Morten Mørup 18

Informatics and Mathematical Modelling / Intelligent Signal Processing channel Channel x Time-Frequency x Subjects j b u S time-frequency Morten Mørup 19 s t ec

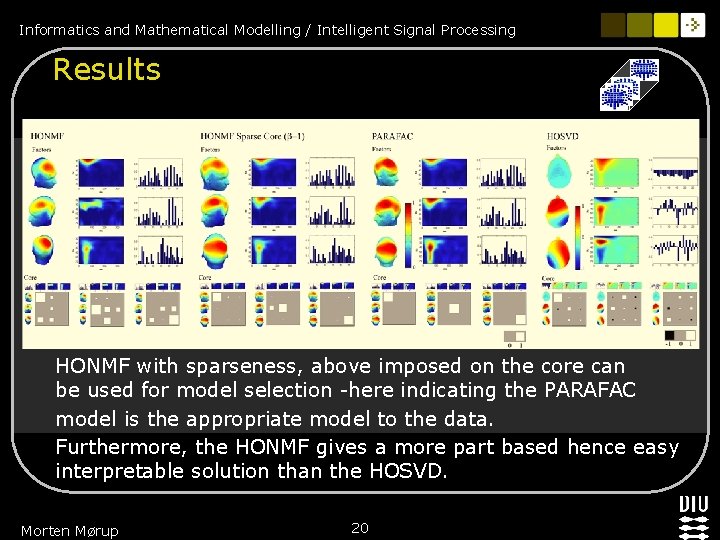
Informatics and Mathematical Modelling / Intelligent Signal Processing Results HONMF with sparseness, above imposed on the core can be used for model selection -here indicating the PARAFAC model is the appropriate model to the data. Furthermore, the HONMF gives a more part based hence easy interpretable solution than the HOSVD. Morten Mørup 20

Informatics and Mathematical Modelling / Intelligent Signal Processing Evaluation of uniqueness Morten Mørup 21

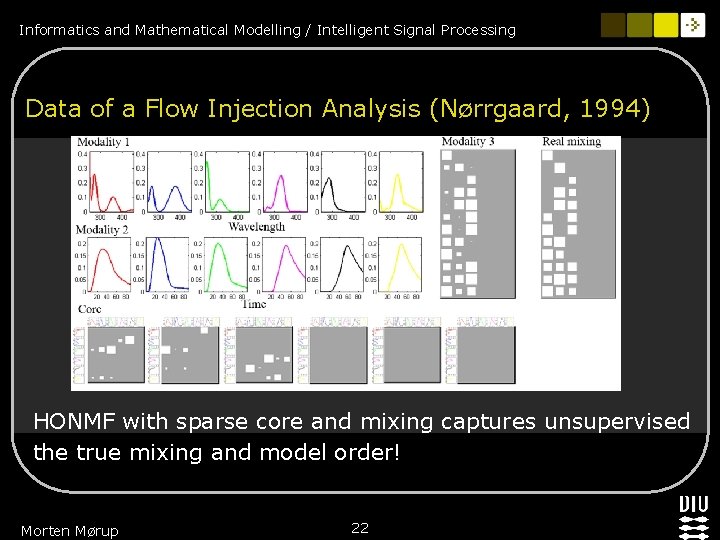
Informatics and Mathematical Modelling / Intelligent Signal Processing Data of a Flow Injection Analysis (Nørrgaard, 1994) HONMF with sparse core and mixing captures unsupervised the true mixing and model order! Morten Mørup 22

Informatics and Mathematical Modelling / Intelligent Signal Processing Many of the data sets previously explored by the Tucker model are nonnegative and could with good reason be decomposed under constraints of non-negativity on all modalities including the core. n Spectroscopy data (Smilde et al. 1999, 2004, Andersson & Bro 1998, Nørgard & Ridder 1994) n Web mining (Sun et al. , 2004) n Image Analysis (Vasilescu and Terzopoulos, 2002, Wang and Ahuja, 2003, Jian and Gong, 2005) n Semantic Differential Data (Murakami and Kroonenberg, 2003) n And many more…… Hopefully, the devised algorithms for sparse non-negative TUCKER will prove useful Morten Mørup 23

Informatics and Mathematical Modelling / Intelligent Signal Processing Conclusion n HONMF and NTF not in general unique, however when imposing sparseness uniqueness can be achieved. n Algorithms devised for LS and KL able to impose sparseness on any combination of modalities n The HONMF decompositions more part based hence easier to interpret than other Tucker decompositions such as the HOSVD. n Imposing sparseness can work as model selection turning of excess components Morten Mørup 24

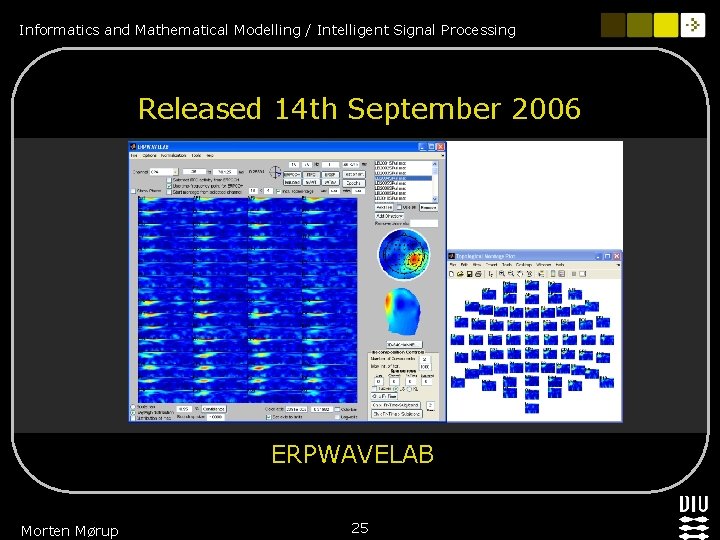
Informatics and Mathematical Modelling / Intelligent Signal Processing Released 14 th September 2006 ERPWAVELAB Morten Mørup 25

Informatics and Mathematical Modelling / Intelligent Signal Processing Sparse Non-negative Tensor Factor double deconvolution for music separation and transcription Morten Mørup 26

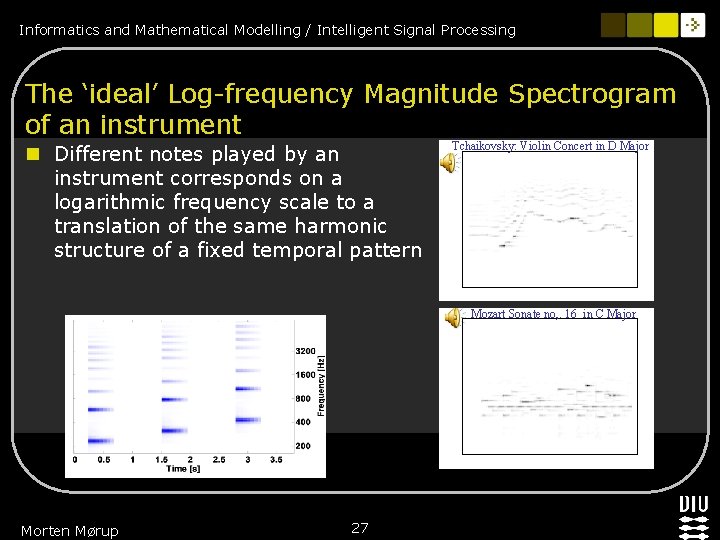
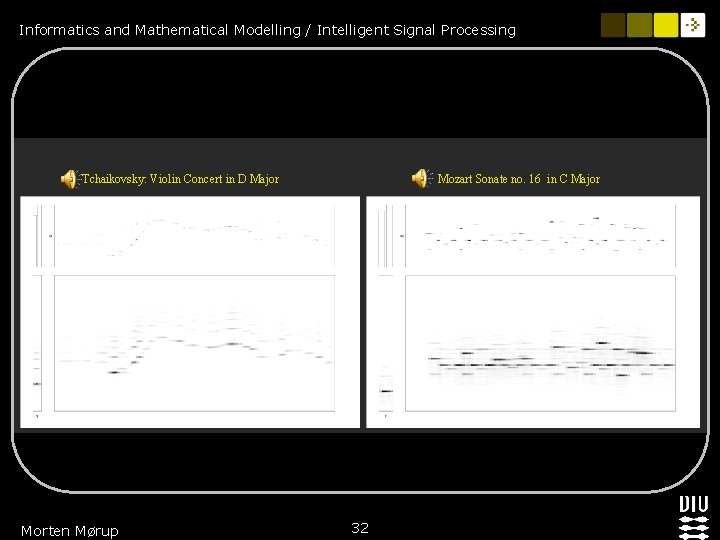
Informatics and Mathematical Modelling / Intelligent Signal Processing The ‘ideal’ Log-frequency Magnitude Spectrogram of an instrument n Different notes played by an instrument corresponds on a logarithmic frequency scale to a translation of the same harmonic structure of a fixed temporal pattern Tchaikovsky: Violin Concert in D Major Mozart Sonate no, . 16 in C Major Morten Mørup 27

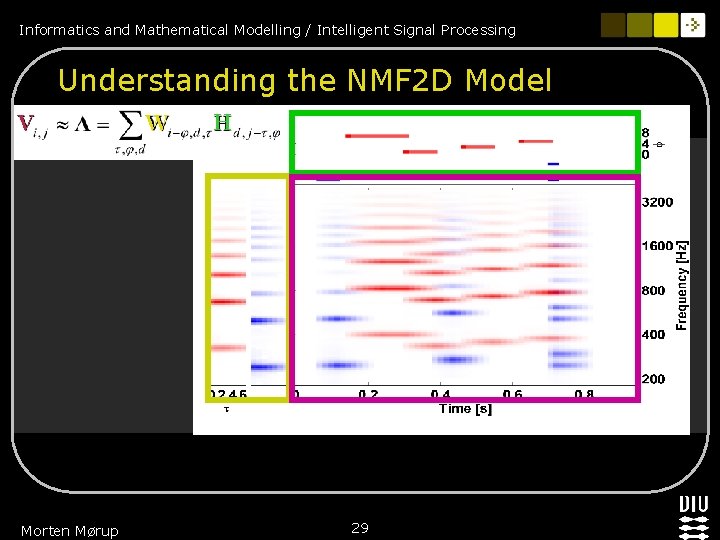
Informatics and Mathematical Modelling / Intelligent Signal Processing NMF 2 D deconvolution (NMF 2 D 1): The Basic Idea n Model a log-spectrogram of polyphonic music by an extended type of non-negative matrix factorization: – The frequency signature of a specific note played by an instrument has a fixed temporal pattern (echo) model convolutive in time – Different notes of same instrument has same time-logfrequency signature but varying in fundamental frequency (shift) model convolutive in the log-frequency axis. (1 Mørup & Scmidt, 2006) Morten Mørup 28

Informatics and Mathematical Modelling / Intelligent Signal Processing Understanding the NMF 2 D Model V Morten Mørup W H 29

Informatics and Mathematical Modelling / Intelligent Signal Processing The NMF 2 D has inherent ambiguity between the structure in W and H To resolve this ambiguity sparsity is imposed on H to force ambiguous structure onto W Morten Mørup 30

Informatics and Mathematical Modelling / Intelligent Signal Processing Real music example of how imposing sparseness resolves the ambiguity between W and H NMF 2 D Morten Mørup 31 SNMF 2 D

Informatics and Mathematical Modelling / Intelligent Signal Processing Tchaikovsky: Violin Concert in D Major Morten Mørup Mozart Sonate no. 16 in C Major 32

Informatics and Mathematical Modelling / Intelligent Signal Processing Sparse Non-negative Tensor Factor 2 D deconvolution (SNTF 2 D) (Extension of Fitzgerald et al. 2005, 2006 to form a sparse double deconvolution) Morten Mørup 33

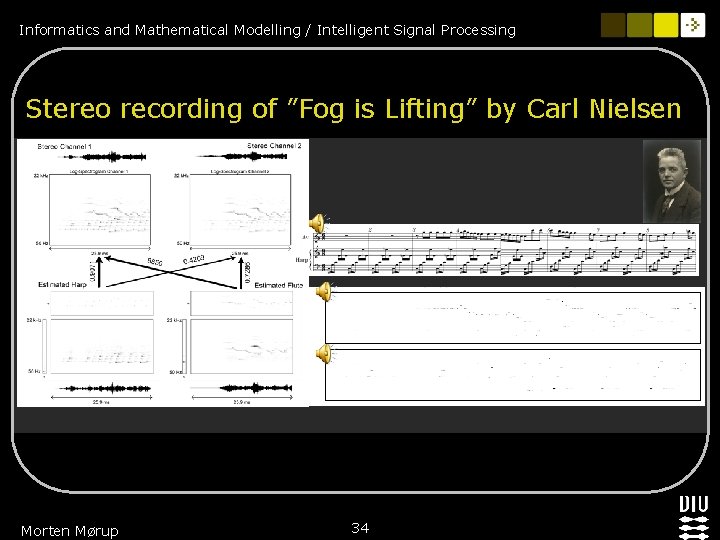
Informatics and Mathematical Modelling / Intelligent Signal Processing Stereo recording of ”Fog is Lifting” by Carl Nielsen Morten Mørup 34

Informatics and Mathematical Modelling / Intelligent Signal Processing Applications n Applications – – Source separation. Music information retrieval. Automatic music transcription (MIDI compression). Source localization (beam forming) Morten Mørup 35

Informatics and Mathematical Modelling / Intelligent Signal Processing References Carroll, J. D. and Chang, J. J. Analysis of individual differences in multidimensional scaling via an N-way generalization of "Eckart-Young" decomposition, Psychometrika 35 1970 283— 319 Donoho, D. and Stodden, V. When does non-negative matrix factorization give a correct decomposition into parts? NIPS 2003 Eggert, J. and Korner, E. Sparse coding and NMF. In Neural Networks volume 4, pages 2529 -2533, 2004 Eggert, J et al Transformation-invariant representation and nmf. In Neural Networks, volume 4 , pages 535 -2539, 2004 Fiitzgerald, D. et al. Non-negative tensor factorization for sound source separation. In proceedings of Irish Signals and Systems Conference, 2005 Fitz. Gerald, D. and Coyle, E. C Sound source separation using shifted non. -negative tensor factorization. In ICASSP 2006, 2006 Fitzgerald, D et al. Shifted non-negative matrix factorization for sound source separation. In Proceedings of the IEEE conference on Statistics in Signal Processing. 2005 Kruskal, J. B. Three-way analysis: rank and uniqueness of trilinear decompostions, with application to arithmetic complexity and statistics. Linear Algebra Appl. , 18: 95 -138, 1977 Harshman, R. A. Foundations of the PARAFAC procedure: Models and conditions for an "explanatory" multi-modal factor analysis}, UCLA Working Papers in Phonetics 16 1970 1— 84 Harshman, Richard A. Harshman and Hong, Sungjin Lundy, Margaret E. Shifted factor analysis—Part I: Models and properties J. Chemometrics (17) pages 379– 388, 2003 Lathauwer, Lieven De and Moor, Bart De and Vandewalle, Joos MULTILINEAR SINGULAR VALUE DECOMPOSITION. SIAM J. MATRIX ANAL. APPL. 2000 (21)1253– 1278 Lee, D. D. and Seung, H. S. Algorithms for non-negative matrix factorization. In NIPS, pages 556 -462, 2000 Lee, D. D and Seung, H. S. Learning the parts of objects by non-negative matrix factorization, NATURE 1999 Lim, Lek-Heng - http: //www. etis. ensea. fr/~wtda/Articles/wtda-nnparafac-slides. pdf Lim, L. -H. and Golub, G. H. , "Nonnegative decomposition and approximation of nonnegative matrices and tensors, " SCCM Technical Report, 06 -01, forthcoming, 2006. Murakami, Takashi and Kroonenberg, Pieter M. Three-Models and Individual Differences in Semantic Differential Data, Multivariate Behavioral Research(38) no. 2 pages 247 -283, 2003 Mørup, M. and Hansen, L. K. and Arnfred, S. M. Decomposing the time-frequency representation of EEG using nonnegative matrix and multi-way factorization Technical report, Institute for Mathematical Modeling, Technical University of Denmark, 2006 b Mørup, M. , Hansen, L. K. , Arnfred, S. M. , ERPWAVELAB A toolbox for multi-channel analysis of time-frequency transformed event related potentials, Journal of Neuroscience Methods, vol. 161, pp. 361 -368, 2007 a Mørup, M. , Hansen, L. K. , Parnes, Josef, Hermann, C, Arnfred, S. M. , Parallel Factor Analysis as an exploratory tool for wavelet transformed event-related EEG Neuroimage Neuro. Image 29 938 – 947, 2006 a Mørup, M. , Schmidt, M. N. , Hansen, L. K. , Shift Invariant Sparse Coding of Image and Music Data, submitted, JMLR, 2007 b Mørup, M. , Hansen, L. K. , Arnfred, S. M. , Algorithms for Sparse Non-negative TUCKER, Submitted Neural Computation, 2006 e Mørup, M. and Hansen, L. K. and Arnfred, S. M. Decomposing the time-frequency representation of EEG using nonnegative matrix and multi-way factorization Technical report, Institute for Mathematical Modeling, Technical University of Denmark, 2006 a Schmidt, M. N. and Mørup, M. Non-negative matrix factor 2 D deconvolution for blind single channel source separation. In ICA 2006, pages 700 -707, 2006 d Nørgaard, L and Ridder, C. Rank annihilation factor analysis applied to flow injection analysis with photodiode-array detection Chemometrics and Intelligent Laboratory Systems 1994 (23) 107 -114 Schmidt, M. N. and Mørup, M. Sparse Non-negative Matrix Factor 2 -D Deconvolution for Automatic Transcription of Polyphonic Music, Technical report, Institute for Mathematical Modelling, Tehcnical University of Denmark, 2005 Smaragdis, P. Non-negative Matrix Factor deconvolution; Extraction of multiple sound sources from monophonic inputs. International Symposium on independent Component Analysis and Blind Source Separation (ICA)W Smilde, Age K. Smilde and Tauller, Roma and Saurina, Javier and Bro, Rasmus, Calibration methods for complex second-order data Analytica Chimica Acta 1999 237 -251 Sun, Jian-Tao and Zeng, Hua-Jun and Liu, Huanand Lu Yuchang and Chen Zheng Cube. SVD: a novel approach to personalized Web search WWW '05: Proceedings of the 14 th international conference on World Wide Web pages 382— 390, 2005 Tamara G. Kolda Multilinear operators for higher-order decompositions technical report Sandia national laboratory 2006 SAND 2006 -2081. Tucker, L. R. Some mathematical notes on three-mode factor analysis Psychometrika 31 1966 279— 311 Welling, M. and Weber, M. Positive tensor factorization. Pattern Recogn. Lett. 2001 Vasilescu , M. A. O. and Terzopoulos , Demetri Multilinear Analysis of Image Ensembles: Tensor. Faces, ECCV '02: Proceedings of the 7 th European Conference on Computer Vision-Part I, 2002 Morten Mørup 36