MATHEMATICAL MODEL Mathematical Model Mathematical Model Mathematical Model

MATHEMATICAL MODEL

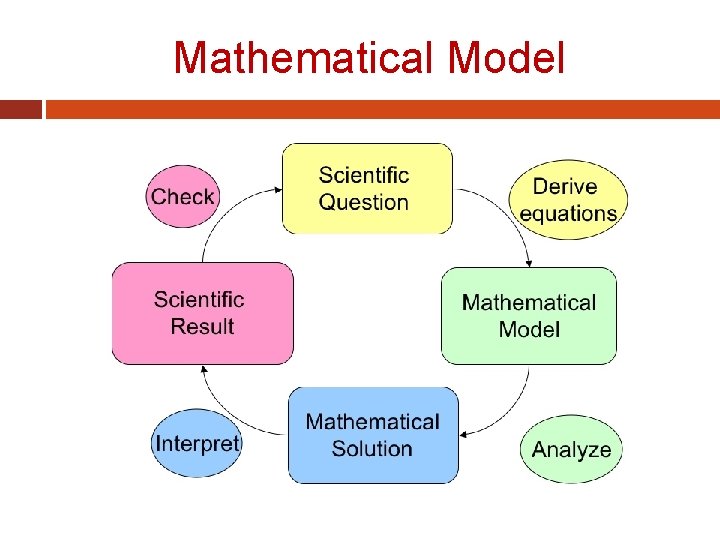
Mathematical Model

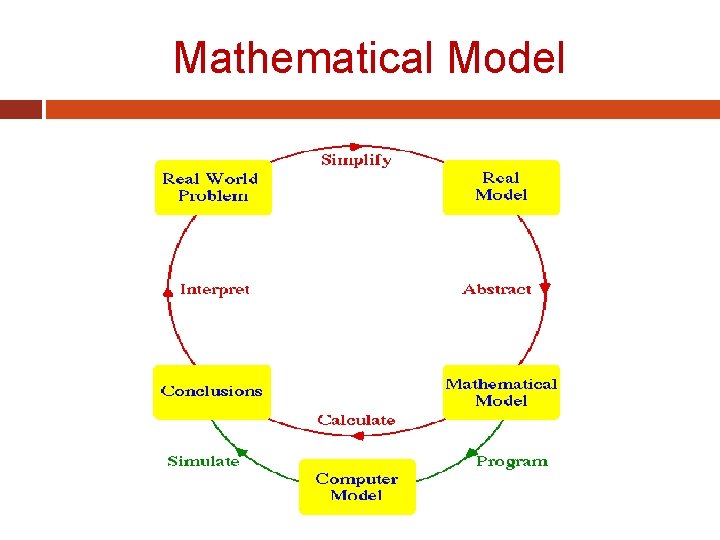
Mathematical Model

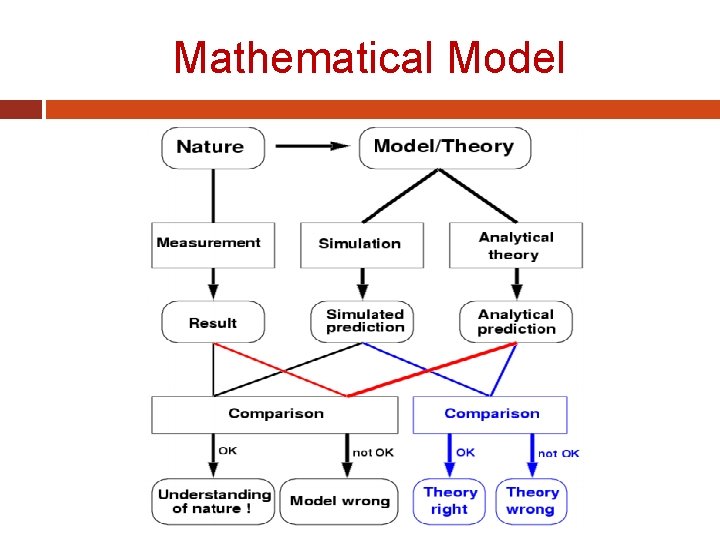
Mathematical Model

Mathematical Model A SIMPLE MATHEMATICAL MODEL �A mathematical model can be broadly defined as a formulation or equation that expresses the essential features of a physical system or process in mathematical terms. In a very general sense, it can be represented as a functional relationship of the form: where the dependent variable is a characteristic that usually reflects the behavior or state of the system; the independent variables are usually dimensions, such as time and space, along which the system’s behavior is being determined; the parameters are reflective of the system’s properties or composition; and the forcing functions are external

Mathematical Model m F where a = the dependent variable reflecting the system’s behavior, F = the forcing function, and m = a parameter representing a property of the system. Note that for this simple case there is no independent variable because we are not yet predicting how acceleration varies in time or space.

Mathematical Model Schematic diagram of the forces acting on a falling parachutist. FD is the downward force due to gravity. FU is the upward force due to air resistance

Mathematical Model

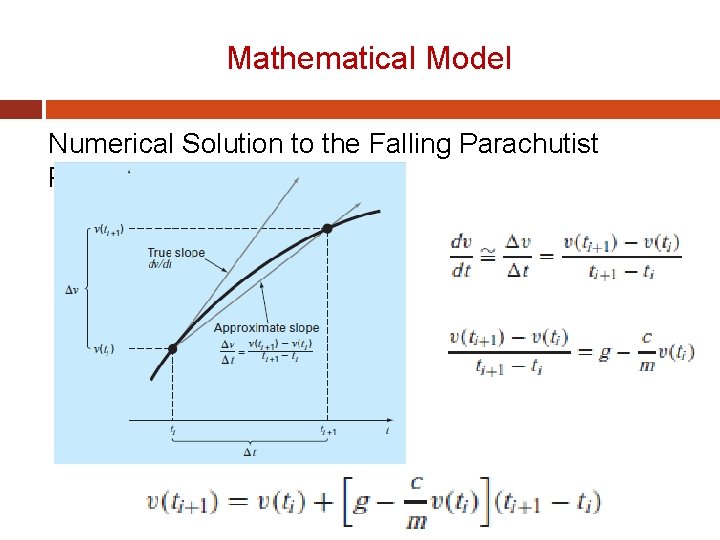
Mathematical Model Numerical Solution to the Falling Parachutist Problem

Mathematical Model

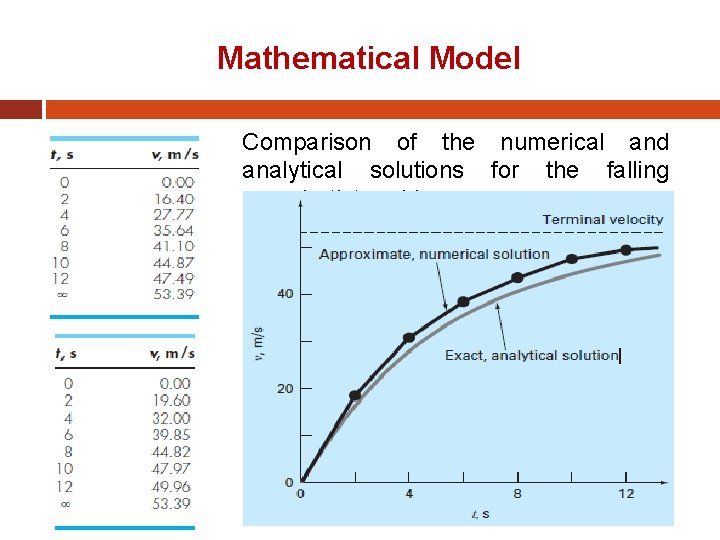
Mathematical Model Comparison of the numerical and analytical solutions for the falling parachutist problem.

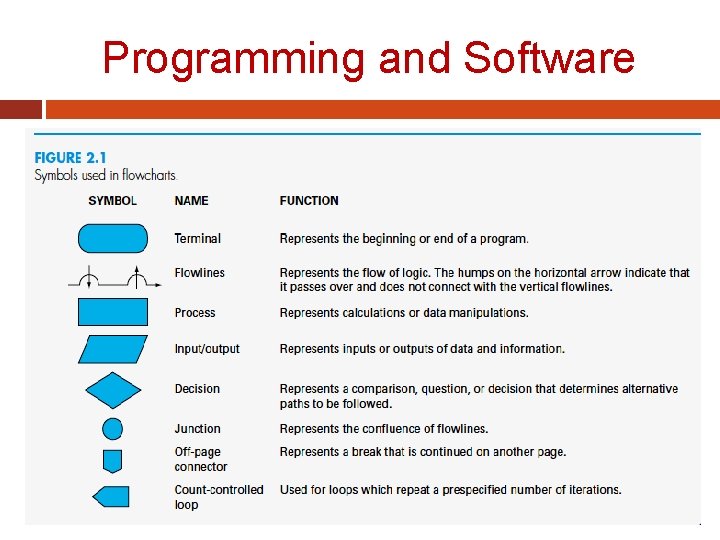
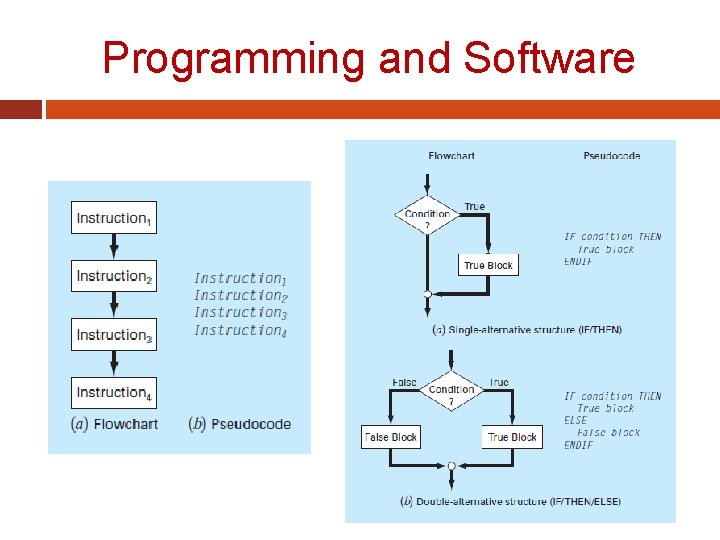
Programming and Software

Programming and Software

Programming and Software

Approximations and Round-Off Errors SIGNIFICANT FIGURES

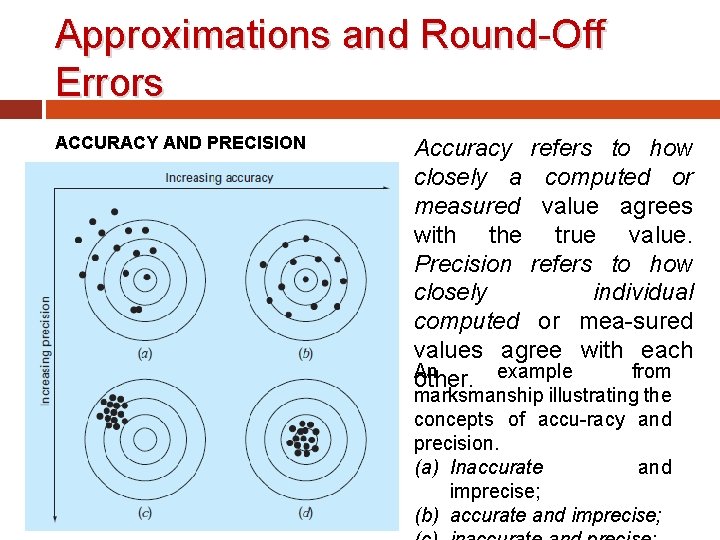
Approximations and Round-Off Errors ACCURACY AND PRECISION Accuracy refers to how closely a computed or measured value agrees with the true value. Precision refers to how closely individual computed or mea-sured values agree with each An from other. example marksmanship illustrating the concepts of accu-racy and precision. (a) Inaccurate and imprecise; (b) accurate and imprecise;

Approximations and Round-Off Errors ERROR DEFINITIONS Numerical errors arise from the use of approximations to represent exact mathematical operations and quantities. These include truncation errors, which result when approximations are used to represent exact mathematical procedures, and round-off errors, which result when numbers having limited significant figures are used to represent exact numbers. the true percent relative error.

Approximations and Round-Off Errors