Inferential statistics 20061 In inferential statistics Data from

Inferential statistics © 20061

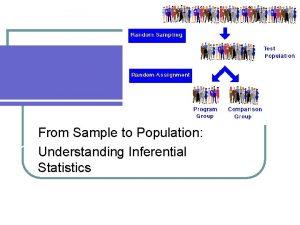
In inferential statistics • Data from samples are used to make inferences about populations • Researchers can make generalizations about an entire population based on a smaller number of observations • However, the sample means will not all be the same when repeated random samples are taken from a population Evidence-based Chiropractic 2 © 2006

Sampling distributions • If many different samples were taken from a population, it would produce a distribution of sample means • If repeated enough times, the distribution would take on a normal shape – Even if the underlying population is not normal • If repeated an infinite number of times, it would be called a sampling distribution Evidence-based Chiropractic 3 © 2006

Sampling distributions (cont. ) • Which of the sample means is truly the population mean? – It would be useful to know, but an exact figure is not possible • The population mean can be inferred from the sample – The sample mean is an estimate – Referred to as the point estimate Evidence-based Chiropractic 4 © 2006

Sampling distributions (cont. ) • Because sampling distributions are normal, the properties of the normal distribution can be used – e. g. , the 68. 3, 95. 5, 99. 7 proportion of the area under the curve Evidence-based Chiropractic 5 © 2006

Standard error of the mean (SEm) • The spread of means around the mean of a sampling distribution • Can be estimated from the sample – SEm is calculated by dividing the SD of the sample by the square root of the number of units in the sample Evidence-based Chiropractic 6 © 2006

SEm (cont. ) • SEm is higher when – The sample’s SD is large or – The sample size is small • Lower when – SD is a small or – The sample size is large • A small SEm is preferable because generalizations are more precise Evidence-based Chiropractic 7 © 2006

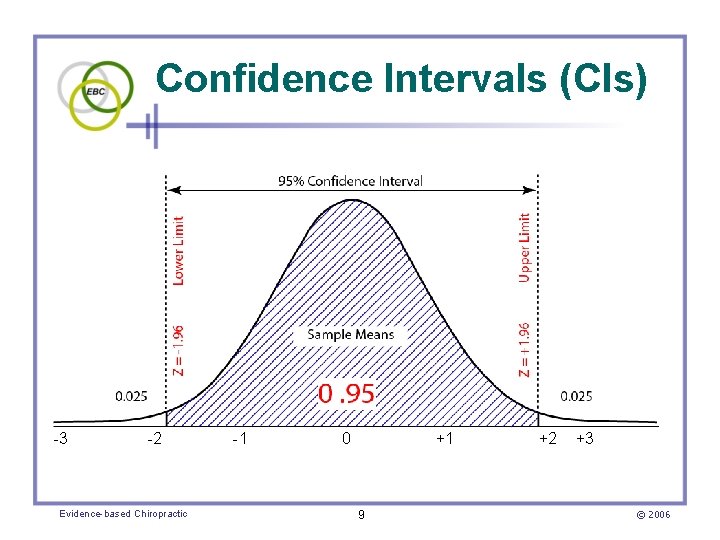
Confidence Intervals (CIs) • A CI is a range of values that is likely to contain the population parameter that is being estimated (e. g. , the mean) • The probability that this range of values contains the population parameter is typically 95% – Thus, the 95% confidence interval Evidence-based Chiropractic 8 © 2006

Confidence Intervals (CIs) -3 -2 Evidence-based Chiropractic -1 0 +1 9 +2 +3 © 2006

CIs (cont. ) • One can have 95% confidence that the value of the true mean lies within the calculated interval (i. e. , 95% CI) Evidence-based Chiropractic 10 © 2006

Calculating a 95% CI 1. Find the z-score (using a z-table) that corresponds to the area under the distribution that includes 95% of all values (e. g. , z = ± 1. 96 for a 95% CI) 2. Multiply the z-scores by the SEm 3. Add the product to the sample mean to find the upper limit of the CI and subtract to find the lower limit Evidence-based Chiropractic 11 © 2006

Size (width) of CIs • The size of the CI is related to the size of the sample and the size of the data variation – Small samples & large variation = larger CIs – Large samples & small variation = smaller CIs Evidence-based Chiropractic 12 © 2006

Hypothesis testing • A hypothesis is an assumption that appears to explain certain events, which must be tested to see whether it is true • Research hypothesis – a. k. a. , alternative hypothesis – Denoted H 1 – The research hypothesis is not tested directly • Instead the null hypothesis (H 0) is tested Evidence-based Chiropractic 13 © 2006

Hypothesis tests • Depending on the outcome of the test of H 0, there is either support for or against the research hypothesis • Hypothesis testing involves the comparison of the means of groups in an experiment – The objective is to find out whether they are significantly different from each other Evidence-based Chiropractic 14 © 2006

Hypothesis tests (cont. ) • When comparing the means of an active treatment group and a control group, one looks for a difference – The treatment may produce a better outcome leading to a higher mean the control group – The difference may appear real, but it may be due to chance – Statistical tests verify if it is real Evidence-based Chiropractic 15 © 2006

The null hypothesis • H 0 states that there is no difference between the group means • H 1 is accepted only if the null hypothesis proves to be unlikely – Typically it must be at least 95% unlikely – If H 0 is unlikely, it is rejected • Not unlike the innocent until proven guilty concept in our legal system Evidence-based Chiropractic 16 © 2006

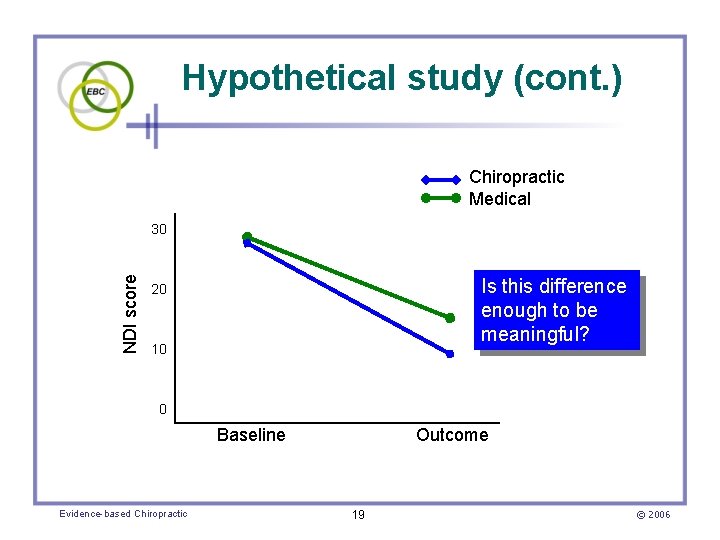
A hypothetical neck pain study • Patients are treated with chiropractic vs. usual medical care – Outcome measure is the Neck Disability Index (NDI) – H 1 • Chiropractic patients will have lower mean NDI scores after treatment – H 0 • There is no difference between mean NDI scores Evidence-based Chiropractic 17 © 2006

Hypothetical study (cont. ) • Results – Mean NDI scores of chiropractic patients • 28 before, 10 after treatment – Mean NDI scores medical patients • 29 before, 15 after treatment • Chiropractic care appears to be better – But is there enough difference to rule out chance – Must perform statistical tests to find out Evidence-based Chiropractic 18 © 2006

Hypothetical study (cont. ) Chiropractic Medical NDI score 30 Is this difference enough to be meaningful? 20 10 0 Baseline Evidence-based Chiropractic Outcome 19 © 2006

Statistical significance • The results of a study (i. e. , the difference between groups) are unlikely to be due to chance – At a specified probability level, referred to as alpha ( ) – is the probability of incorrectly rejecting a null hypothesis • If the results are not due to chance, H 0 is rejected and H 1 is accepted Evidence-based Chiropractic 20 © 2006

Statistical significance (cont. ) • It must be at least 95% unlikely that H 0 is true before it can be rejected • There is still a 5% chance that H 0 would be rejected, when it was actually true • Accordingly, P values must be equal to or less than 5% in order for the results of a study to reach a level of statistical significance Evidence-based Chiropractic 21 © 2006

Statistical significance (cont. ) • The level of significance (alpha level) is not the same as the P value – The alpha level must be set before the study begins – The P value is calculated at the completion of the study and must be ≤ to the alpha level in order to reach statistical significance Evidence-based Chiropractic 22 © 2006

Statistical significance (cont. ) • Even when studies are not statistically significant, there is a 1: 20 chance that significant results would occur if the study was repeated 20 times • Fishing – When researchers perform a lot of statistical tests on their data – Increases the chance that at least one of the tests will wrongly reach statistical significance Evidence-based Chiropractic 23 © 2006

Type I & II errors • Type I error (a. k. a. , alpha error) – Rejecting a true null hypothesis – The probability of making a Type I error is equal to the value of α • Type II error (a. k. a. , beta error ) – Failure to reject a false null hypothesis – The probability of making a Type II error is equal to the value of beta ( ) Evidence-based Chiropractic 24 © 2006

Type I & II errors (cont. ) Consequences of accepting or rejecting true and false null hypotheses Evidence-based Chiropractic 25 © 2006

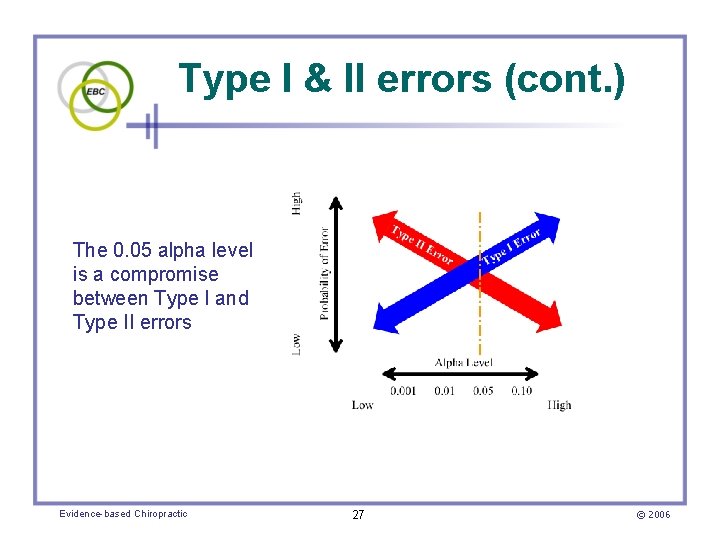
Type I & II errors (cont. ) • There is a trade-off between the likelihood of a study resulting in a Type I error versus a Type II error • As alpha becomes smaller, the chance of making a Type I error decreases • Whereas the chance of making a Type II error increases – Because it is more likely that a false H 0 will not be rejected Evidence-based Chiropractic 26 © 2006

Type I & II errors (cont. ) The 0. 05 alpha level is a compromise between Type I and Type II errors Evidence-based Chiropractic 27 © 2006

Power • The probability of correctly rejecting a false H 0 – Related to error – Power is equal to 1 - • Power depends on sample size, the magnitude of the difference between group means, and the value of α Evidence-based Chiropractic 28 © 2006

Power (cont. ) • Power increases as – Sample size increases • Only to a certain extent, then it becomes a waste of resources – The difference between group means increases – α increases • A power value of 0. 80 is often sought by researchers Evidence-based Chiropractic 29 © 2006

Power (cont. ) • Power may be calculated after a study has been completed (post hoc) – If low power is detected during post hoc power analysis and H 0 was not rejected, it may be grounds to repeat the study using a larger sample Evidence-based Chiropractic 30 © 2006

Confidence intervals and hypothesis testing • If the value specified as the difference between group means in the null hypothesis is included in the 95% CI, then H 0 should not be rejected – The test is not statistically significant • H 0 states there is no difference between group means, so the specified no difference value is always zero Evidence-based Chiropractic 31 © 2006

CIs and hypothesis testing (cont. ) • If zero is not included in the 95% CI, the null hypothesis should be rejected – The test is statistically significant • CIs are becoming more prevalent in the health care literature because they convey more information than P values alone Evidence-based Chiropractic 32 © 2006

CIs and hypothesis testing (cont. ) • Example study – Brinkhaus et al. – Acupuncture was more effective in improving pain on VAS* than no acupuncture in chronic low back pain patients • Difference, 21. 7 mm (95% CI 13. 9 to 30. 0) – But no statistical difference between acupuncture and minimal acupuncture • Difference, 5. 1 mm (95% CI -3. 7 to 13. 9) * Visual analog scale Evidence-based Chiropractic 33 © 2006

Clinical significance a. k. a. , practical significance • Do the findings of a study really matter in clinical situations • Sometimes a study is statistically significant, but the findings are not important in clinical terms – Large studies with small differences between groups can generate statistically significant findings that are not meaningful to practitioners Evidence-based Chiropractic 34 © 2006

Clinical significance (cont. ) • For example – A study found a statistically significant difference between mean Headache Disability Inventory (HDI) scores of only 10 points – Yet at least a 29 -point change must occur from test to retest before the changes can be attributed to a patient’s treatment • The HDI is not very responsive to change Evidence-based Chiropractic 35 © 2006

Commonly encountered statistical tests • Statistical tests determine the probabilities associated with relationships in studies – Are the results real or merely due to chance? • t-test, ANOVA, and chi-square common in journal articles – Familiarity with these tests is helpful in the appraisal of articles Evidence-based Chiropractic 36 © 2006

t-test • Used to find out whether the means of two groups are statistically different • Results are not entirely black-and-white – Only indicates that the means are probably different – Or, that they are probably the same, if the study fails to find a difference • The t-test can be used for a single group by comparing the mean with known values Evidence-based Chiropractic 37 © 2006

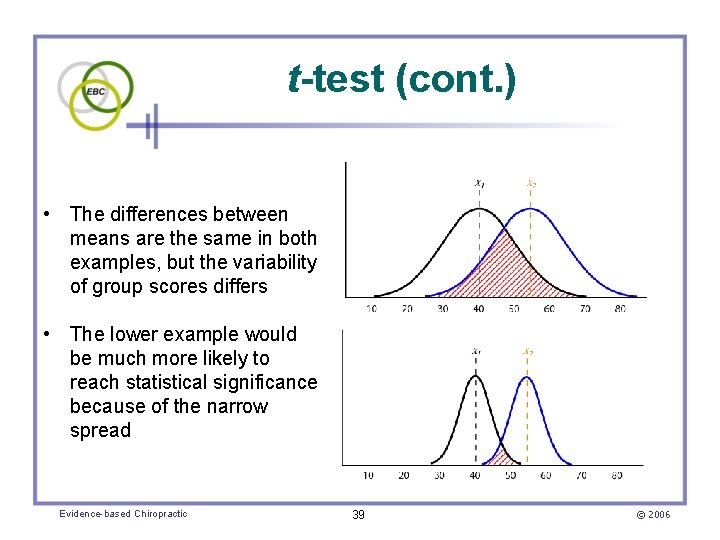
t-test (cont. ) • The actual differences between means is considered • Also the amount of variability of the scores – A high degree of variability of group scores can obscure the differences between means Evidence-based Chiropractic 38 © 2006

t-test (cont. ) • The differences between means are the same in both examples, but the variability of group scores differs • The lower example would be much more likely to reach statistical significance because of the narrow spread Evidence-based Chiropractic 39 © 2006

Assumptions of the t-test • The data should be normal and involve interval or ratio measurement • Groups should be independent • The variances of groups should be equal • When the sample size is large enough (about 30 subjects) violations of these assumptions are less important Evidence-based Chiropractic 40 © 2006

Alternatives to the t-test • The t-test for unequal variances • Non-parametric tests for use with skewed data – Mann-Whitney U test – Wilcoxon test Evidence-based Chiropractic 41 © 2006

The t-score • The t-score (a. k. a. , t-ratio) is similar to the z-score – However, the t-distribution and a t-table are used – This is because the SD of the population is estimated from the sample, whereas it is known in the z-distribution • P values are found using the calculated t-score and a t-table Evidence-based Chiropractic 42 © 2006

The t-score (cont. ) • t-tables consider the number of subjects in the groups • Referred to as degrees of freedom (df) – Signifies the number of subjects in each group minus 1 – Minus 2 when there are two groups – Thus, a study that compares the means of 2 groups that involve 30 subjects has 28 df Evidence-based Chiropractic 43 © 2006

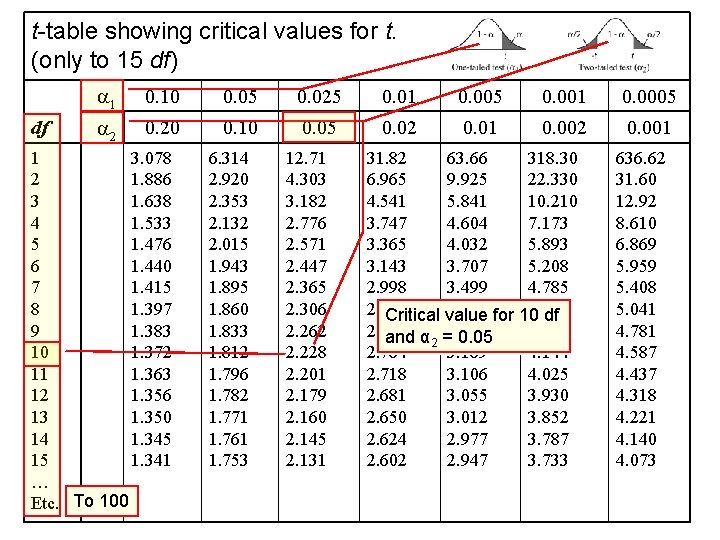
The t-table • t-distributions eventually become nearly normal when many subjects are included – As a result, t-tables usually only go to 100 df • Alpha levels are shown for – When α is all in one tail (α 1 or one-tailed test ) – When α is spit between the tails (α 2 or twotailed test) Evidence-based Chiropractic 44 © 2006

t-table showing critical values for t. (only to 15 df) df 1 0. 10 0. 05 0. 025 0. 01 0. 005 0. 001 0. 0005 2 0. 20 0. 10 0. 05 0. 02 0. 01 0. 002 0. 001 1 3. 078 2 1. 886 3 1. 638 4 1. 533 5 1. 476 6 1. 440 7 1. 415 8 1. 397 9 1. 383 10 1. 372 11 1. 363 12 1. 356 13 1. 350 14 1. 345 15 1. 341 … To 100 Etc. Evidence-based Chiropractic 6. 314 2. 920 2. 353 2. 132 2. 015 1. 943 1. 895 1. 860 1. 833 1. 812 1. 796 1. 782 1. 771 1. 761 1. 753 12. 71 4. 303 3. 182 2. 776 2. 571 2. 447 2. 365 2. 306 2. 262 2. 228 2. 201 2. 179 2. 160 2. 145 2. 131 31. 82 63. 66 318. 30 6. 965 9. 925 22. 330 4. 541 5. 841 10. 210 3. 747 4. 604 7. 173 3. 365 4. 032 5. 893 3. 143 3. 707 5. 208 2. 998 3. 499 4. 785 2. 896 3. 355 for 10 4. 501 Critical value df 2. 821 4. 297 and α 2 =3. 250 0. 05 2. 764 3. 169 4. 144 2. 718 3. 106 4. 025 2. 681 3. 055 3. 930 2. 650 3. 012 3. 852 2. 624 2. 977 3. 787 2. 602 2. 947 3. 733 45 636. 62 31. 60 12. 92 8. 610 6. 869 5. 959 5. 408 5. 041 4. 781 4. 587 4. 437 4. 318 4. 221 4. 140 4. 073 © 2006

One-tailed test vs. two-tailed test • One-tailed test (a. k. a. , directional test) – Alpha is all in one tail – The researcher specifies the direction the test results will go before the data analysis • Either higher or lower • Two-tailed test (a. k. a. , non-directional test) – Alpha is split between the tails – The study’s results could go either way Evidence-based Chiropractic 46 © 2006

One-tailed test vs. two-tailed test (cont. ) • In a non-directional test, the researcher wants to know if the means are different – For example, in a study comparing manipulation with acupuncture for tension headaches, the results could go either way – That is the case with almost all studies that compare treatments Evidence-based Chiropractic 47 © 2006

One-tailed test vs. two-tailed test (cont. ) • It is easier to reach statistical significance using a directional test – Consequently it is tempting for researchers to use directional hypotheses • The opposite direction must be of no interest to the researcher – But it is almost always possible for the test to go either way when comparing treatments Evidence-based Chiropractic 48 © 2006

Calculating the t-score • Is a ratio of the difference between group means and the variability of the data • Variability is represented by the standard error of the difference ( ) rather than the SD • Thus or Evidence-based Chiropractic 49 © 2006

The t-score • For the t-test result to be statistically significant – The difference between the means must be large (the numerator) – And the variability of the data must be small (the denominator) • This results in a t-score that is larger than the critical value of t in the t-table Evidence-based Chiropractic 50 © 2006

The t-score (cont. ) • Remember Big t-value Small P value Statistical significance Evidence-based Chiropractic 51 © 2006

Steps involved in the t-test • Calculate the means and standard deviations of the groups’ outcomes • Calculate the t-ratio • Check to see if the calculated t is statistically significant using a t-table • It is significant if t is greater than the critical value of t at the 0. 05 level • If so, the group means are considered different Evidence-based Chiropractic 52 © 2006

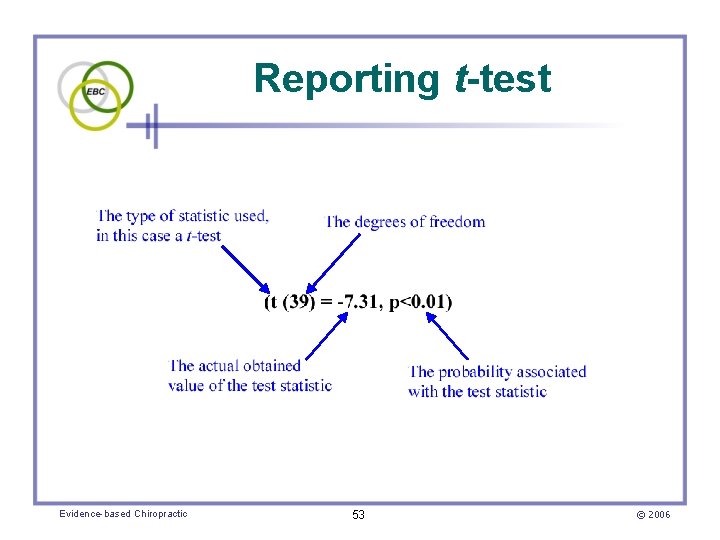
Reporting t-test Evidence-based Chiropractic 53 © 2006

Paired t-test • Groups are dependent – The same subjects are in each of the groups • e. g. , repeated measures studies – Or subjects are matched • e. g. , twins or when subjects are very much alike Evidence-based Chiropractic 54 © 2006

Analysis of variance (ANOVA) • Used to compare means when more than two groups are involved • Repeating t-tests increases the probability of producing a Type I error • ANOVA can only compare one outcome variable – Univariate Evidence-based Chiropractic 55 © 2006

ANOVA (cont. ) • ANOVA provides information about – Whethere any significant differences among the group means – Whether any of the particular groups differ from each other – Whether the differences are relatively big or small Evidence-based Chiropractic 56 © 2006

The F-ratio • Not unlike the t-ratio, the F-test compares the variance between the groups with the variance within the groups variance between groups F = variance within the groups Evidence-based Chiropractic 57 © 2006

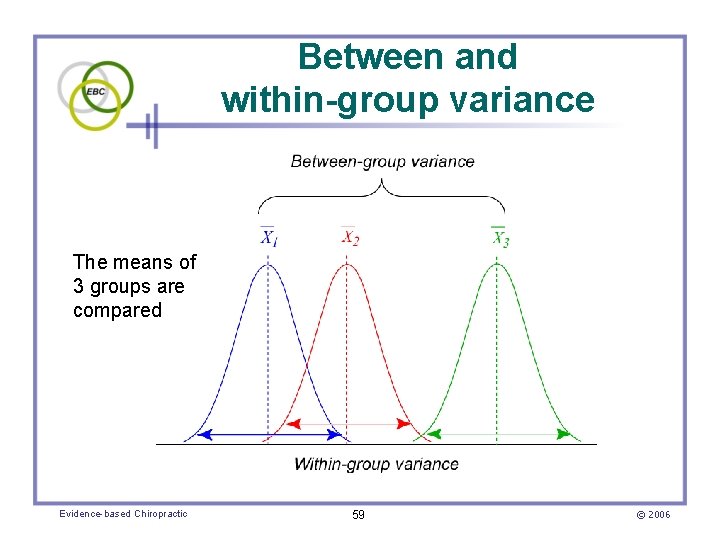
The F-ratio (cont. ) • Within-group variance is related to sampling error and ordinary differences between subjects – For instance, many physical characteristics vary normally (e. g. , cortisol levels, pulse rate, and blood pressure) • Between-group variance is related to the differences between the means Evidence-based Chiropractic 58 © 2006

Between and within-group variance The means of 3 groups are compared Evidence-based Chiropractic 59 © 2006

The F-ratio (cont. ) • • • If the F-ratio is small, the groups are probably not significantly different If it is big, at least two of the groups are significantly different The F- test does not identify which of the groups are different – Comparison tests are necessary Evidence-based Chiropractic 60 © 2006

Comparison tests • Compare the group pairs (pairwise) • Common comparison tests include – Tukey • Used if the groups are of unequal size – Bonferroni • For both equal and unequal group sizes – Scheffé • Is very conservative to minimize the risk of type I error Evidence-based Chiropractic 61 © 2006

Microsoft Excel has several built-in statistical functions • Excel can be used to calculate ANOVA, t-ratio, and others • Select Data Analysis from the Tools menu and input the data Evidence-based Chiropractic 62 © 2006

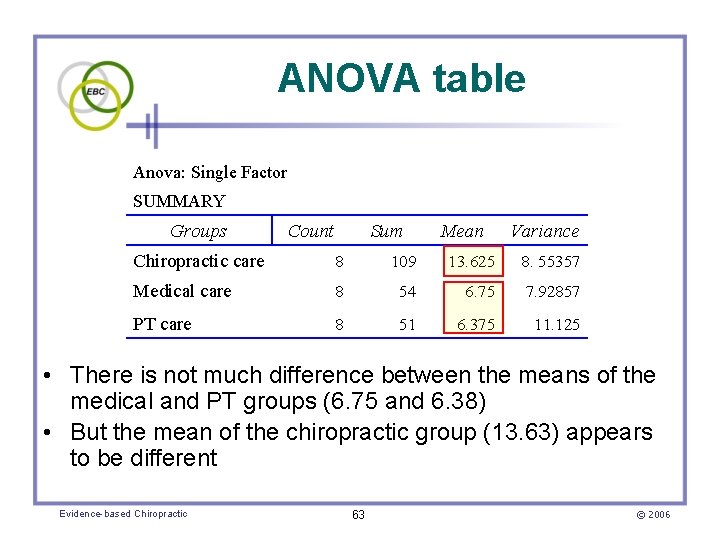
ANOVA table Anova: Single Factor SUMMARY Groups Count Sum Mean Variance Chiropractic care 8 109 13. 625 8. 55357 Medical care 8 54 6. 75 7. 92857 PT care 8 51 6. 375 11. 125 • There is not much difference between the means of the medical and PT groups (6. 75 and 6. 38) • But the mean of the chiropractic group (13. 63) appears to be different Evidence-based Chiropractic 63 © 2006

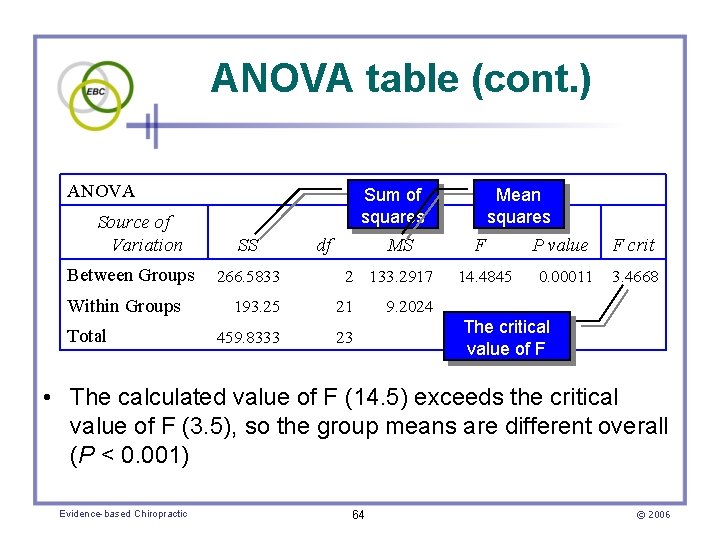
ANOVA table (cont. ) ANOVA Source of Variation Between Groups Within Groups Total Sum of squares SS 266. 5833 193. 25 459. 8333 df Mean squares MS F 2 133. 2917 21 23 14. 4845 P value F crit 0. 00011 3. 4668 9. 2024 The critical value of F • The calculated value of F (14. 5) exceeds the critical value of F (3. 5), so the group means are different overall (P < 0. 001) Evidence-based Chiropractic 64 © 2006

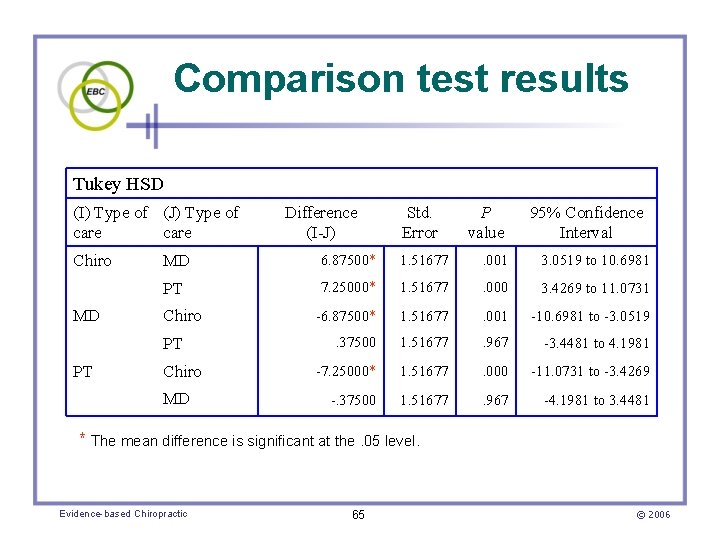
Comparison test results Tukey HSD (I) Type of (J) Type of care Difference (I-J) Std. Error P value 95% Confidence Interval Chiro MD 6. 87500* 1. 51677 . 001 3. 0519 to 10. 6981 PT 7. 25000* 1. 51677 . 000 3. 4269 to 11. 0731 MD Chiro -6. 87500* 1. 51677 . 001 -10. 6981 to -3. 0519 PT . 37500 1. 51677 . 967 -3. 4481 to 4. 1981 PT Chiro -7. 25000* 1. 51677 . 000 -11. 0731 to -3. 4269 -. 37500 1. 51677 . 967 -4. 1981 to 3. 4481 MD * The mean difference is significant at the. 05 level. Evidence-based Chiropractic 65 © 2006

Assumptions of ANOVA test • • Normally distributed data Groups should be independent Variances of groups should be equal If not, a nonparametric test should be used – Kruskal-Wallis test • When variances are unequal – Friedman test • When paired groups are involved Evidence-based Chiropractic 66 © 2006

Chi-square test • Used to test hypotheses involving categorical data • There are 2 versions – Chi-square goodness of fit • Determines if observed frequencies of occurrence differ from what would be expected by chance – Chi-square test of independence • Tests to see if frequencies for one category differ significantly from those of another category Evidence-based Chiropractic 67 © 2006

Chi-square goodness of fit • Called the goodness of fit test because it tests whether observed frequencies “fit” against the expected frequencies • For example – If a sample of Americans found 60 males and 40 females, would that be statistically significantly different from what would normally be expected (50/50)? Evidence-based Chiropractic 68 © 2006

Goodness of fit example (cont. ) 2 • Chi-square (Χ ) calculates the difference between the observed and expected frequencies, then divides that value by the 2 expected frequencies to generate the Χ statistic Χ 2 = Σ(O-E) E 2 O – observed frequencies E – expected frequencies Evidence-based Chiropractic 69 © 2006

Goodness of fit example (cont. ) • Following are the calculations for the 100 Americans example Observed 2 (60 – 50) Χ = 50 2 Expected + (40 – 50)2 50 Χ 2 = 4. 0 Evidence-based Chiropractic 70 © 2006

Goodness of fit example (cont. ) • A chi-square table is used to see if the results are statistically significant – Only if the critical value is exceeded (3. 84 in this case) • df is the number of categories minus 1 2 • The calculated Χ is 4 – So, the sample is different from what was expected Evidence-based Chiropractic 71 © 2006

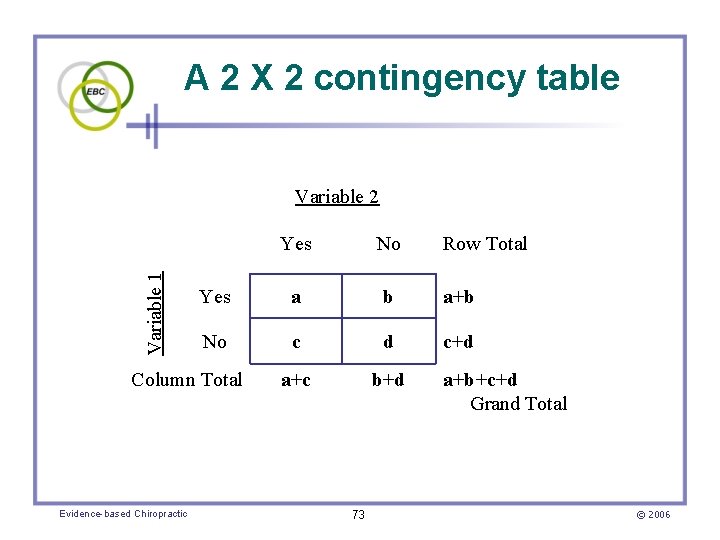
Chi-square test of independence • Frequencies of one variable are compared with another to see if they differ significantly • A 2 X 2 contingency table (a. k. a. , crosstabulation table) is used Evidence-based Chiropractic 72 © 2006

A 2 X 2 contingency table Variable 1 Variable 2 Yes No Yes a b a+b No c d c+d a+c b+d Column Total Evidence-based Chiropractic 73 Row Total a+b+c+d Grand Total © 2006

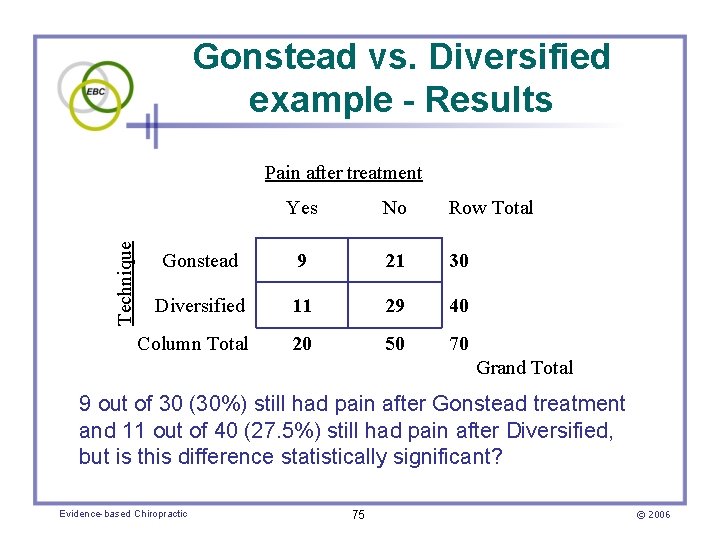
Example hypothetical study • Two groups of patients are treated using different spinal manipulation techniques – Gonstead vs. Diversified • The presence or absence of pain after treatment is the outcome measure • Two categories – Technique used – Pain after treatment Evidence-based Chiropractic 74 © 2006

Gonstead vs. Diversified example - Results Pain after treatment No Row Total 9 21 30 Diversified 11 29 40 Column Total 20 50 70 Technique Yes Gonstead Grand Total 9 out of 30 (30%) still had pain after Gonstead treatment and 11 out of 40 (27. 5%) still had pain after Diversified, but is this difference statistically significant? Evidence-based Chiropractic 75 © 2006

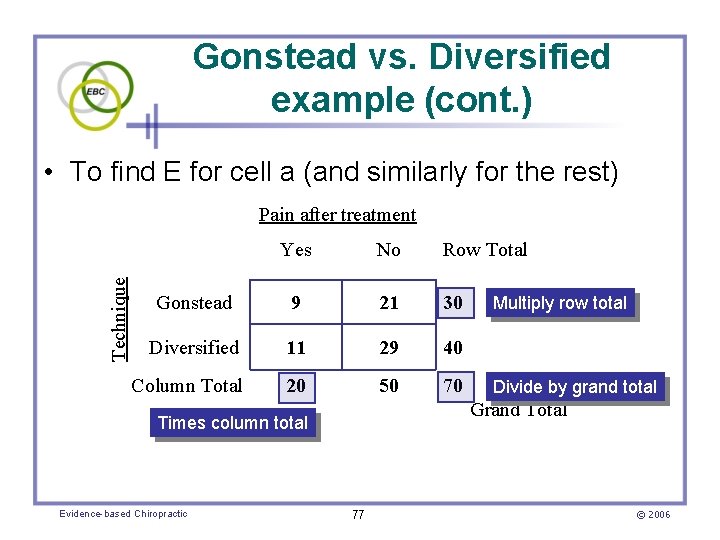
Gonstead vs. Diversified example (cont. ) 2 • Calculating Χ • First find the expected values for each cell Expected (E) = Row total Χ Column total Grand total • Then calculate the Χ 2 statistic using the cells’ expected (E) values and the previously provided 2 Χ formula Evidence-based Chiropractic 76 © 2006

Gonstead vs. Diversified example (cont. ) • To find E for cell a (and similarly for the rest) Pain after treatment No Row Total 9 21 30 Diversified 11 29 40 Column Total 20 50 70 Technique Yes Gonstead Divide by grand total Grand Total Times column total Evidence-based Chiropractic Multiply row total 77 © 2006

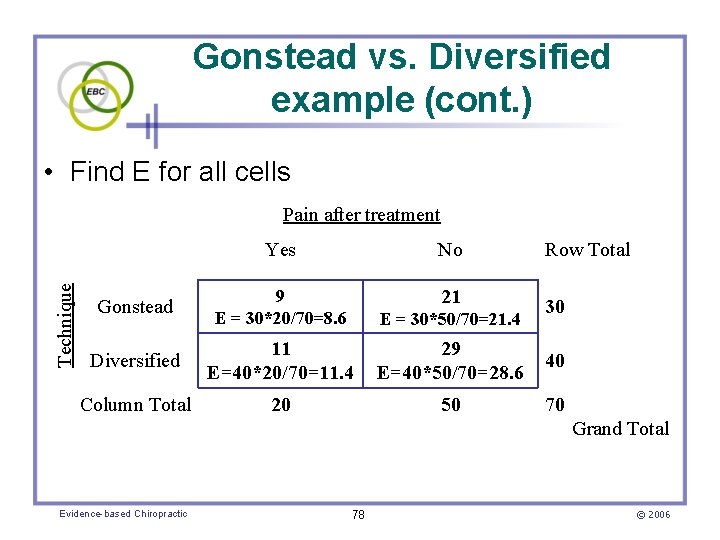
Gonstead vs. Diversified example (cont. ) • Find E for all cells Technique Pain after treatment Yes No Row Total Gonstead 9 E = 30*20/70=8. 6 21 E = 30*50/70=21. 4 Diversified 11 E=40*20/70=11. 4 29 E=40*50/70=28. 6 40 Column Total 20 50 70 30 Grand Total Evidence-based Chiropractic 78 © 2006

Gonstead vs. Diversified example (cont. ) 2 • Use the Χ formula with each cell and then add them together (9 - 8. 6)2 8. 6 (21 - 21. 4)2 21. 4 (11 - 11. 4)2 (29 - 28. 6)2 11. 4 28. 6 0. 0186 0. 0168 = 0. 0316 0. 0056 Χ 2 = 0. 0186 + 0. 0168 + 0. 0316 + 0. 0056 = 0. 0726 Evidence-based Chiropractic 79 © 2006

Gonstead vs. Diversified example (cont. ) 2 • Find df and then consult a Χ table to see if statistically significant – df = (number of categories for variable 1) -1 X (number of categories for variable 2) -1 • There are two categories for each variable in this case, so df = 1 • Critical value at the 0. 05 level and one df is 3. 84 2 – Therefore, Χ is not statistically significant Evidence-based Chiropractic 80 © 2006

2 Χ required conditions • Observations must be independent – The total number of observed frequencies should not be higher than the number of subjects in the study • No small expected frequencies – Expected frequencies less than one or less than five in more than 20 percent of cells are too small Evidence-based Chiropractic 81 © 2006

2 Χ requirements (cont. ) – Fisher's exact test • An alternative to the chi-square test that is used when expected frequencies are too small • All that is needed is at least one data value in each row and one data value in each column • No extremely small or extremely large samples – Extremely small samples may overlook obvious false null hypotheses and extremely large samples may identify trivial differences Evidence-based Chiropractic 82 © 2006

Correlation • A measure of mathematical relationships that may exist between two or more variables – i. e. , if one variable increases or decreases, the other one will also increase or decrease a specific amount • Pearson’s correlation coefficient (r) is commonly used Evidence-based Chiropractic 83 © 2006

Correlation (cont. ) • Correlation coefficient values range from -1 to +1 +1 = perfect positive correlation -1 = perfect negative correlation • The closer r is to +1 or -1, the more closely variables are related Evidence-based Chiropractic 84 © 2006

Correlation (cont. ) • Positive r values – Variables tend to go up or down together • Negative r values – Variables tend to go up and down in opposition • An r value of 0 – There is no mathematical relationship between variables Evidence-based Chiropractic 85 © 2006

Correlation (cont. ) • The units of measurement that are used do not affect correlation coefficient calculations – e. g. , height and weight results will be the same whether in and lb or cm and kg are used in the calculation Evidence-based Chiropractic 86 © 2006

No cause-and-effect • A strong relationship between two variables does not mean that one caused the other to change • For instance, there is a strong relationship between coffee drinking and developing lung cancer – Actually, heavy coffee drinkers tend to be heavy smokers – Smoking is the actual cause Evidence-based Chiropractic 87 © 2006

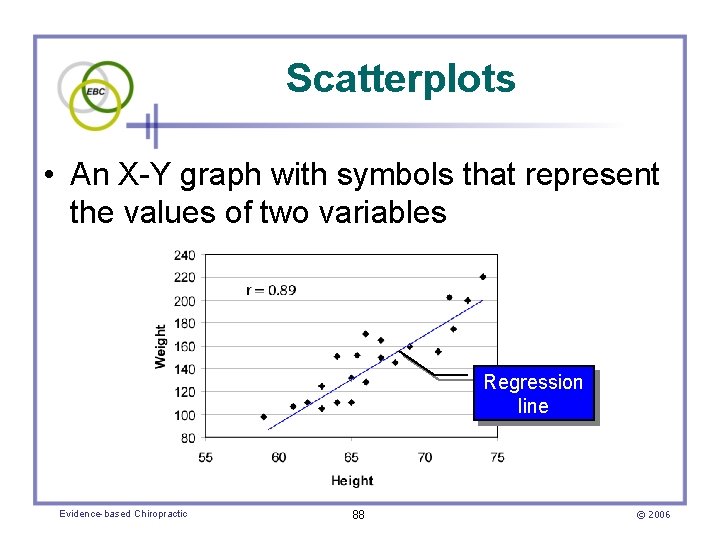
Scatterplots • An X-Y graph with symbols that represent the values of two variables Regression line Evidence-based Chiropractic 88 © 2006

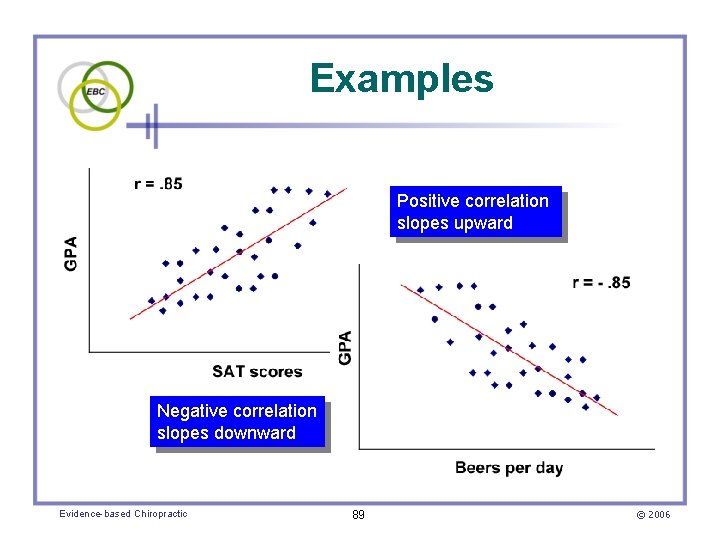
Examples Positive correlation slopes upward Negative correlation slopes downward Evidence-based Chiropractic 89 © 2006

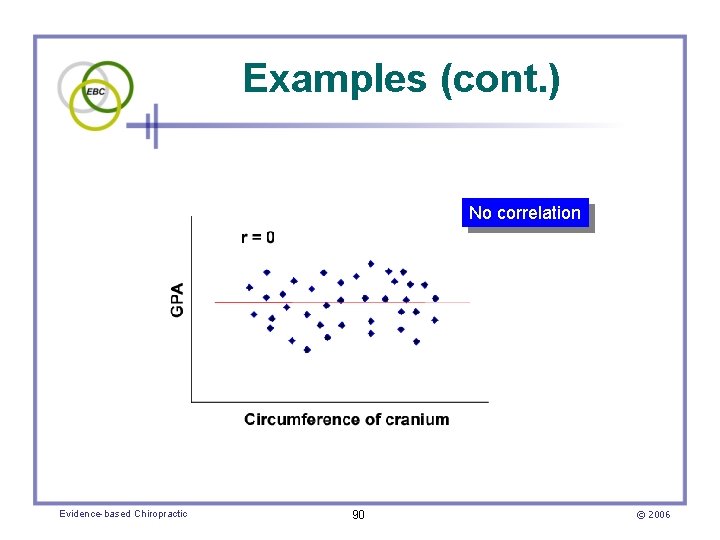
Examples (cont. ) No correlation Evidence-based Chiropractic 90 © 2006

Scatterplots (cont. ) • Show the form, direction, and strength of the relationship between variables • Its form may be linear, but can also be curvilinear or nonlinear • A correlation weakens after a certain point when data is curvilinear Evidence-based Chiropractic 91 © 2006

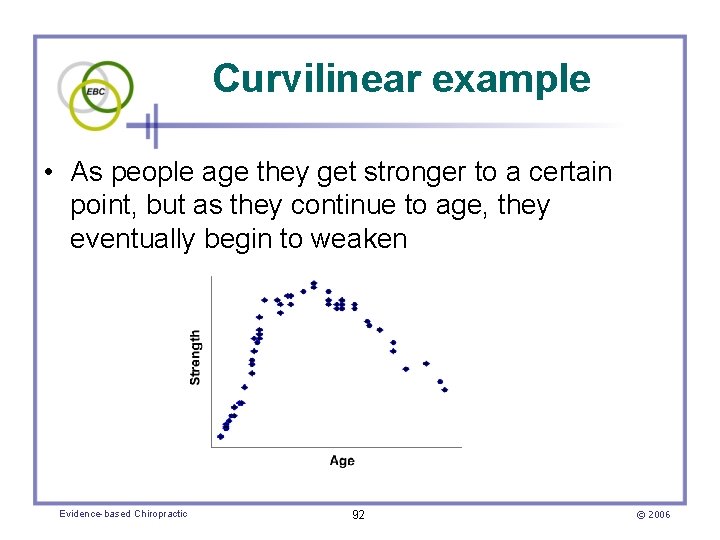
Curvilinear example • As people age they get stronger to a certain point, but as they continue to age, they eventually begin to weaken Evidence-based Chiropractic 92 © 2006

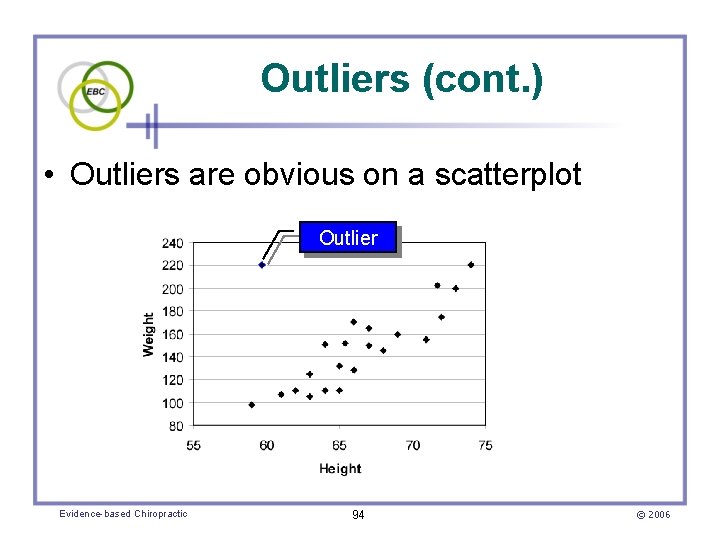
Outliers • Extreme values that are located far away from the group of data on a scatterplot • Outliers can strongly influence the slope of the regression line – And the value of the correlation coefficient • Authors should adequately discuss outliers – Why they occurred – How they were dealt with Evidence-based Chiropractic 93 © 2006

Outliers (cont. ) • Outliers are obvious on a scatterplot Outlier Evidence-based Chiropractic 94 © 2006

Coefficient of determination • Is the correlation coefficient squared – Symbolized as r 2 • Only positive values are possible (because it is squared) – Ranging from 0 to 1 • Denotes how much of the variation in one variable can be explained by the other variable Evidence-based Chiropractic 95 © 2006

Coefficient of determination • Example – If a study on the relationship between the amount lifted at work and the incidence of lowback pain reported r 2 as 0. 65 – One could say that 65% of the variability in the incidence of low-back pain was explained by the amount workers lifted – Other factors are responsible for the remaining 35% variability Evidence-based Chiropractic 96 © 2006

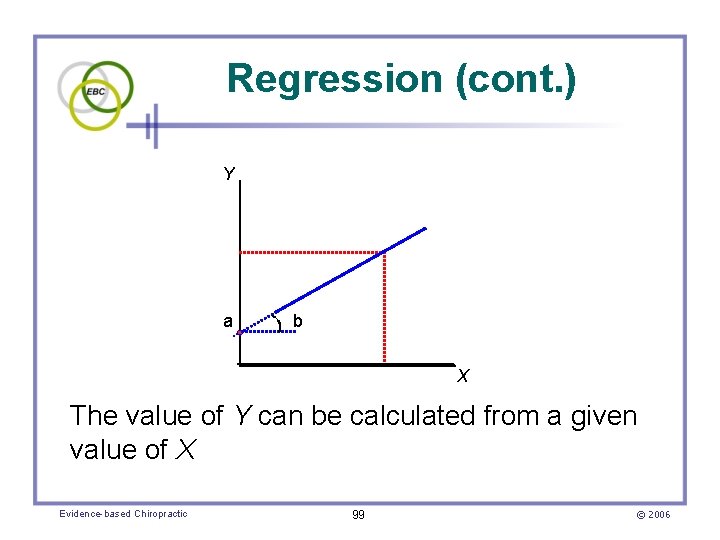
Regression • Regression analysis – Calculation of the line of best fit passing through a set of data – An equation is generated that describes the line of best fit (a. k. a. , least squares line) • Using the equation, predictions can be made about the direction and amount variables change Evidence-based Chiropractic 97 © 2006

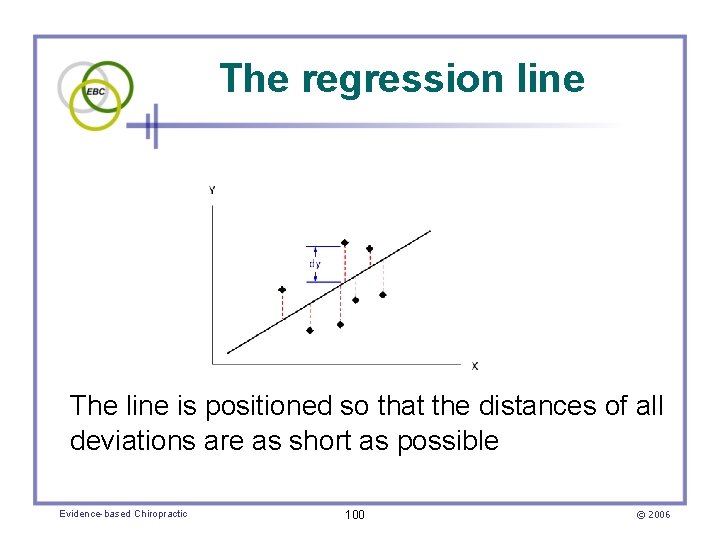
Regression (cont. ) • A regression line is fitted by minimizing the sum of squared deviations of the data points from the least squares line • The regression equation is Y = a + b. X, where – a is the Y intercept – b is the slope of the line – X is the value of the (predictor) variable Evidence-based Chiropractic 98 © 2006

Regression (cont. ) Y a b X The value of Y can be calculated from a given value of X Evidence-based Chiropractic 99 © 2006

The regression line The line is positioned so that the distances of all deviations are as short as possible Evidence-based Chiropractic 100 © 2006

Multiple regression • Frequently outcomes are affected by more than one predictor variable • The multiple regression equation is similar to simple regression, but with more than one value for b. Thus, the equation is Y = a + b 1 X 1 + b 2 X 2 +. . . + bk. Xk, where • X 1 is the first predictor variable, X 2 is the second, and Xk continues for as many predictor variables as are involved Evidence-based Chiropractic 101 © 2006