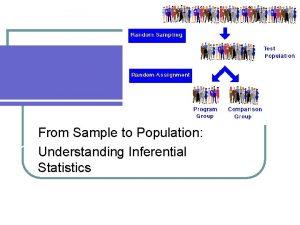
Inferential statistics PSY 4010 Central concepts in inferential

Inferential statistics PSY 4010

Central concepts in inferential statistics: n Sampling error n Sampling distribution n Standard error n Null hypothesis and alternative hypothesis n Level of significance n Type I and Type II error n One-tailed and two-tailed tests n Degrees of freedom n Parametric and non-parametric statistical tests n Effect size

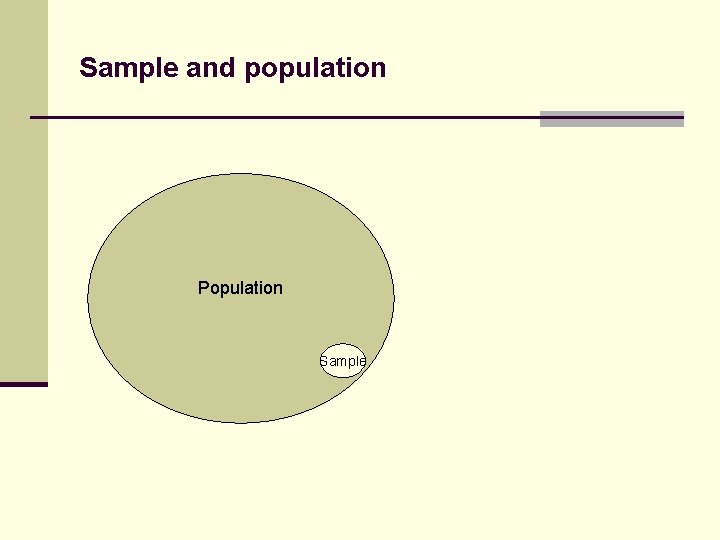
Sample and population Population Sample

Example: IQ-mean score in population and sample n The population mean IQ-score equals 100 ( =100) and the standard deviation is 15 ( = 15) n You draw three samples consisting of 25 randomly selected persons from this population and estimates the mean IQ score in each sample : Sampling error (coincidence results in deviation from population mean score) Sample 1: Sample 2 Sample 3 101 98 103 -100 = 3 101 -100 = 1 98 -100 = -2

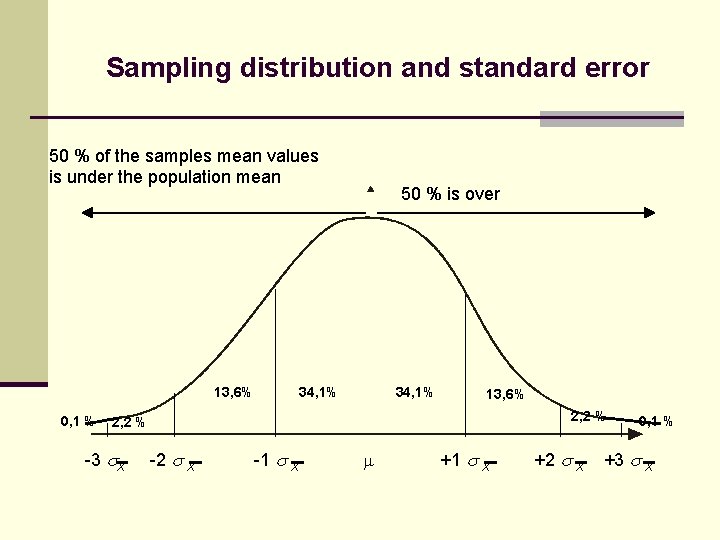
Sampling distribution and standard error n Sampling distribution: n Distribution of the mean values of an infinitive number of samples of the same size drawn from the same population n Can also be other measures then mean values, e. g. Correlation coefficients, regression coefficients n The standard deviation of such a sampling distribution is called the standard error n A very important measure, an estimate of variability in mean scores due to chance (sampling error)

Standard error n. The standard error is a function of two things: n n : How large the standard deviation in the population is N: The size of the sample Examples based on samples drawn from a population with a standard deviation( ) of 15 (and mean of 100) n. N=9 n N = 25 n N = 100

Sampling distribution at different sample sizes Infinitive number of samples randomly drawn from a population with N = 100 and standard deviation = 15 N = 25 N=9 85 90 95 100 105 110 115

Sampling distribution and standard error 50 % of the samples mean values is under the population mean 13, 6% 0, 1 % 50 % is over 34, 1% 13, 6% 2, 2 % -3 X -2 X -1 X +2 X 0, 1 % +3 X

Example: IQ and breast-feeding n The population mean score on IQ for 12 years old is 100 and the standard deviation is 15 n A researcher suspects that breast-feeding can affect IQ n A sample of 25 12 -year olds being breast-fed up to six months of age have a mean IQ-score of 103 n How probable is it that this sample has sampling error? = 103 due to

Testing hypotesis Null hypothesis (H 0): The population of children being breast-fed up to 6 months of age does not have a different mean IQ score from other children I. e. : the difference from the population mean score is due to sampling error Alternative hypothesis (H 1): The population of children being breast -fed up to 6 mnds of age does have a different mean IQ score from the population of other children How probable is it to obtain a difference of 3 points or more in mean score due to sampling error/pure chance? This is referred to as the p-value

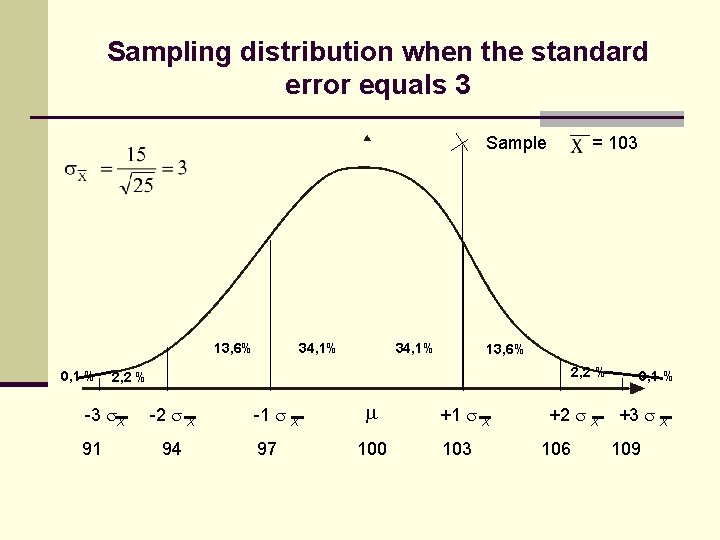
Sampling distribution when the standard error equals 3 Sample 13, 6% 0, 1 % 34, 1% 13, 6% 2, 2 % -3 X 91 34, 1% = 103 -2 X 94 -1 X 97 100 +1 X 103 +2 X 106 0, 1 % +3 X 109

How probable is it that the results is due to random variation (sampling error)? In our example: a of 103 or higher will appear in 15, 9 % (p= 0. 159) of all the N = 25 samples we draw from a population with =100, = 15 Thus, the probability of sampling error is 15, 9 %

Significance level The limit we set in order to reject H 0 is called significance level ( ) : - Convention: if the probability sampling error is less than 5 %, we reject the Null hypothesis. - If the probability of sampling error is 5 % or more, keep H 0 - We usually symbolize this as = 0. 05 - We can also set the level to 1 % or lower ( = 0. 01) - Based on the results, we……. keep H 0

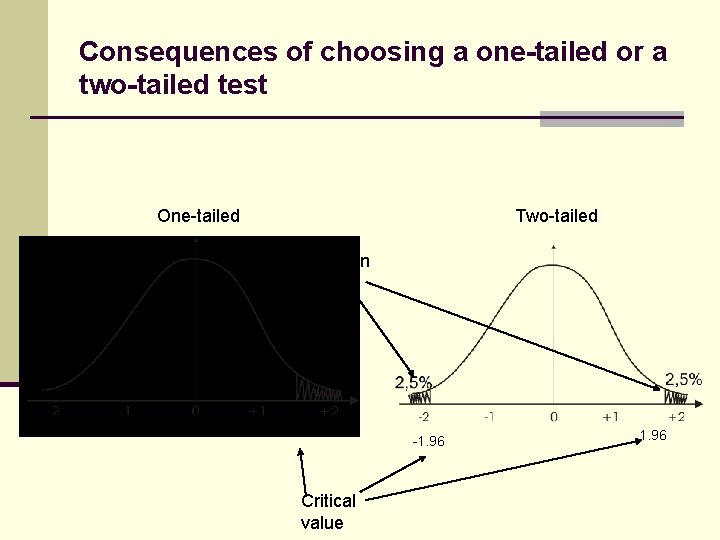
One-tailed and two-tailed tests n A one-tailed test: the difference is in an expected direction: H 0 : (The population) of children who are breast-fed up to 6 mnds of age have higher mean IQ-score than other children n A two-tailed test H 1 : (The population) of children who are breast-fed up to 6 mnds of age have a different mean IQ-score than other children (Thus, we open up for the possibility that the mean IQ-score of breast-fed children can be either lower or higher than in the population of other children) n Important to decide upon one- ore two-tailed test before the test is conducted!

Consequences of choosing a one-tailed or a two-tailed test One-tailed Two-tailed Rejection area 1. 65 Critical value -1. 96

Task 1 We now have increased our a sample to 100 children who have been breast-fed up to 6 mnds of age. The sample’s mean score on IQ is the same: 103 If you choose a level of significance of 5 % ( =. 05), do you reject or keep H 0?

Type I and Type II error We can never be 100% sure that we do the right thing when rejecting or keeping H 0: In the population (the true world) H 0 is true The sample value is due to sampling error H 0 is false The sample is drawn from a population with a different mean value Decision: Keep H 0 Correct decision Type II-error Decision: Reject H 0 Type I-error (equals α) Correct decision THUS: We do not say that H 0 is true or false, or that H 1 is so.

What do we do when we do not know the population values? n We use the sample’s standard deviation (s) as an estimate of the population‘s standard deviation ( ) n Standard error if we know population standard deviance: n In practice: (small) samples often underestimate the standard deviation in the population n Therefore, this is taken into consideration in the test for significance applied n Most applied; the student t- distribution n Standard error if we do not know population standard deviance:

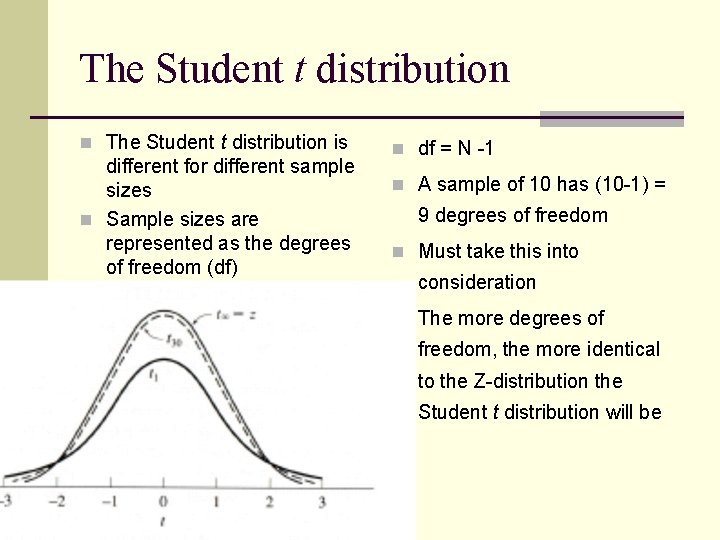
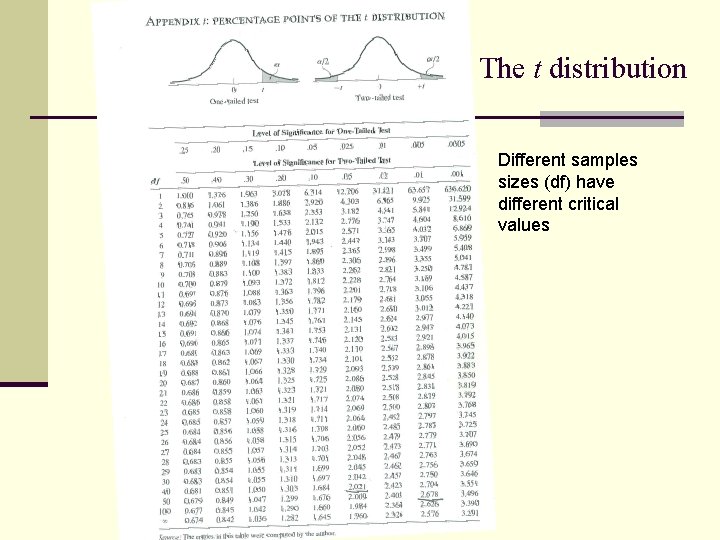
The Student t distribution n The Student t distribution is different for different sample sizes n Sample sizes are represented as the degrees of freedom (df) n df = N -1 n A sample of 10 has (10 -1) = 9 degrees of freedom n Must take this into consideration n The more degrees of freedom, the more identical to the Z-distribution the Student t distribution will be

The t distribution Different samples sizes (df) have different critical values

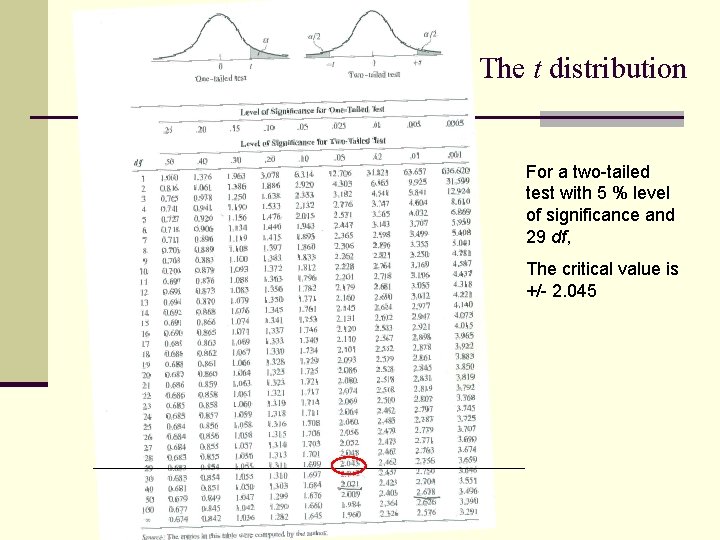
When the population’s standard deviation is not known Example: do drivers’ mean speed deviate from the speed limit when it is raised to 100 km/h on a road section? You measured the speed of 30 cars. These have: n What is the critival value for H 0: µ = 100 H 1: µ ≠ 100 rejecting H 0 at a 5 % level? n df = N-1 = 30 -1 = 29

The t distribution For a two-tailed test with 5 % level of significance and 29 df, The critical value is +/- 2. 045

-5, 47 -2, 045 Our estimated t-value is in the rejection area, and we reject H 0 Thus, we believe that the real driving speed is below 100 km/h

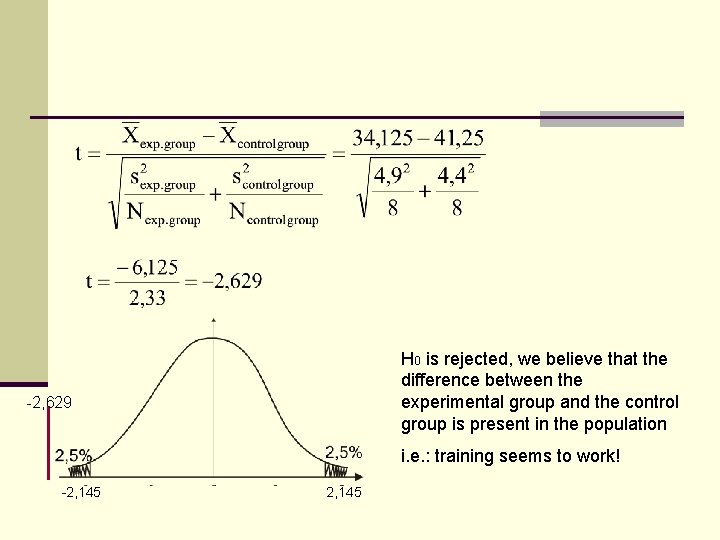
Difference in mean score between two samples, no information about population values Is the difference between the experimental group (N =8) and control group (N =8) on mean depression score after treatment statistically significant? Null hypothesis (H 0): Alternative hypothesis (H 1): How probable is it that the difference in due to sampling error?

H 0 is rejected, we believe that the difference between the experimental group and the control group is present in the population -2, 629 i. e. : training seems to work! -2, 145

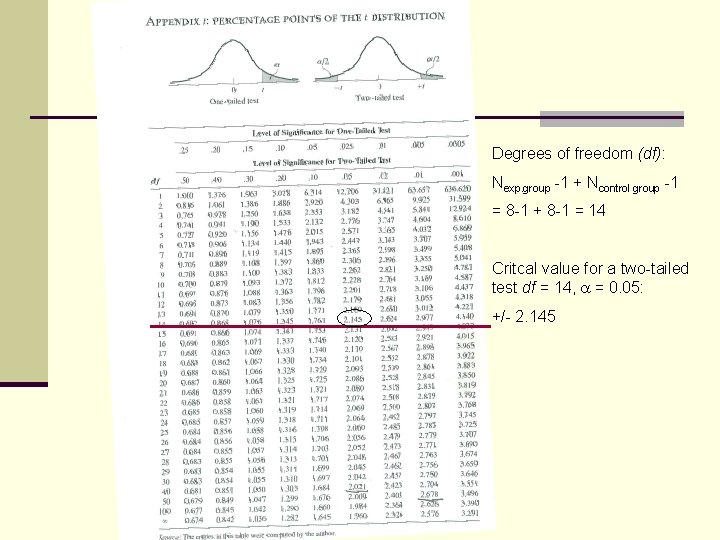
Degrees of freedom (df): Nexp. group -1 + Ncontrol group -1 = 8 -1 + 8 -1 = 14 Critcal value for a two-tailed test df = 14, = 0. 05: +/- 2. 145

Parametric tests n Parametric tests are based upon three main assumptions 1. The sample(s) is randomly drawn from the population 2. The values are normally distributed in the population 3. If two or more samples are compared to each other, they must be drawn from populations with equal variances This are very rigid assumption. However, parametric tests are quite robust to violation of assumption 2 and 3

Examples of parametric tests Applied when we know the population values (mean score, standard deviation, or percentage etc. ) n Z-test Applied when we do not know the population values n t-test (difference in mean scores between groups, correlation and regression coefficients) n F-test (Analysis of variance)

Non-parametric tests n Applied when assumptions of parametric tests are violated n Or when dependent variables are on a ordinal/nominal level n Basically the same logic is applied as for significance testing using parametric tests

Example of a non-parametric test: the chisquare test ( 2) n Is being found guilty or not for violent crimes dependent upon skin color? Not guilty Guilty Total Light skin 70 30 100 Dark skin 30 70 100 Total 100 n Both variables are measured on a nominal level, and mean and standard deviation cannot be estimated n In this case we use the chi- square test ( 2) to determine whether the difference is significant or not

Core of the chi-square test Calculate the expected values (E) which symbolize the values if there were no relationship between the two variables Not guilty Guilty Light skin Observed (O) =70 Expected (E) = 50 O = 30 E = 50 Dark skin O = 30 E = 50 O = 70 E = 50 n Compare these to the observed values (O) using this formula:

n We must also estimate the number of freedom: df = (the number of columns -1) + (the number of rows-1) df = (2 -1) + (2 -1) = 1 n And next find the critical value of 2 at a 5 % level of significance n H 0: there is no association between skin color and being found guilty n H 1: there is an association between skin color and being found guilty

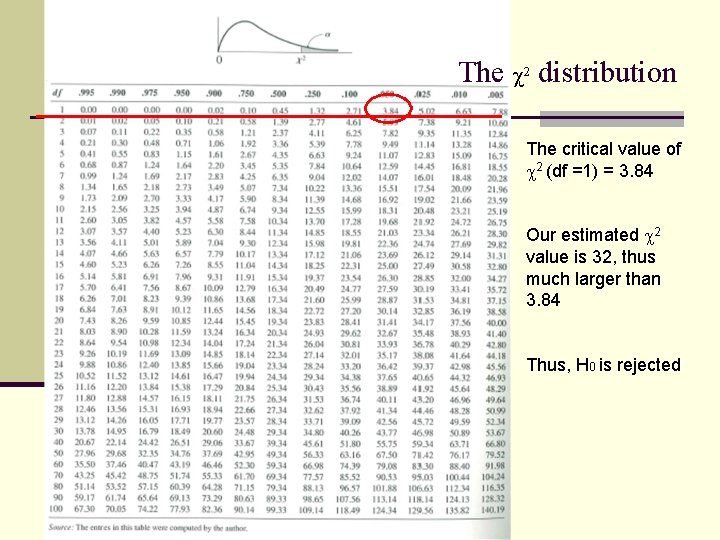
The 2 distribution The critical value of 2 (df =1) = 3. 84 Our estimated 2 value is 32, thus much larger than 3. 84 Thus, H 0 is rejected

Level of significance and practical importance/significance n A statistical significant result is not necessary of large practical importance n The main reason: statistical significant result is strongly influenced by the size of the sample(s) n Large samples = easy to obtain significant results (i. e. easier to reject H 0) n Small samples = difficult to obtain significant results n Useful to include a measure of effect size also n Focusing on how large the difference is/ how strong the association between the variables are

Effect size Several types: For differences in mean n D-value: (difference relative to standard deviation) Interpretation of d d= 0, no difference +/- 0. 20: small difference +/- 0. 50: moderate difference +/-. 80: large difference For measures of association and explained variance: n r, r 2 and R 2 n Eta 2

Random sampling 1. Simple randomized sampling n All members of the population have an equal chance of being drawn 2. Systematic sampling n Selected using a certain key n E. g. . Each 50 th person over 18 year 3. Stratified randomized sampling Random selection within subgroups of the population 4. Proportionate sampling. Drawing certain proportions of the sample from subgroups of the population 5. Cluster sampling. Drawing all members of randomly selected groups from the population (e. g. school classes)

Non-random samples 1. Convenience sampling n Students attending a lecture, stopping people on the street, voluntary participants 2. Quota sampling n Recruit volunteers, but make sure that certain characteristics are represented in certain proportions (e. g. equal number of each gender, age etc. )