CORRELATIONS Inferential Statistics Overview Correlation coefficients Scatterplots Calculating

CORRELATIONS Inferential Statistics

Overview Correlation coefficients Scatterplots Calculating Pearson’s r Interpreting correlation coefficients Calculating & interpreting coefficient of determination Determining statistical significance Calculating Spearman’s correlation coefficient

Correlation Reflects the degree of relation between variables � Calculation of correlation coefficient Direction + (positive) or – (negative) Strength (i. e. , magnitude) Further away from zero, the stronger the relation � Form of the relationship

Check yourself Indicate whether the following statements suggest a positive or negative relationship: � High school students with lower IQs have lower GPAs � More densely populated areas have higher crime rates � Heavier automobiles yield poorer gas mileage � More anxious people willingly spend more time performing a simple repetitive task

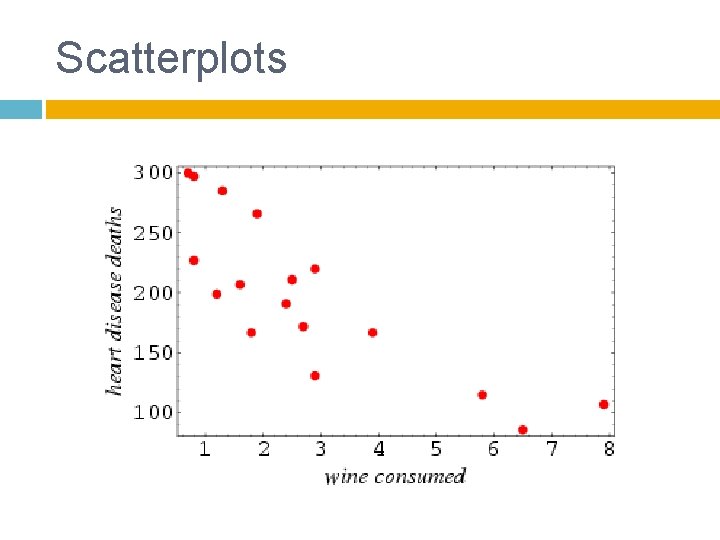
Scatterplots

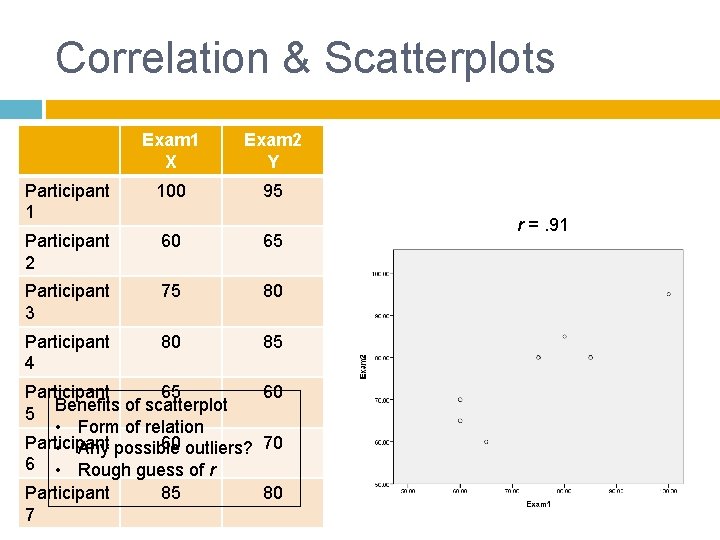
Correlation & Scatterplots Exam 1 X Exam 2 Y Participant 1 100 95 Participant 2 60 65 Participant 3 75 80 Participant 4 80 85 Participant 65 60 Benefits of scatterplot 5 • Form of relation Participant 60 outliers? 70 • Any possible 6 • Rough guess of r Participant 85 80 7 r =. 91

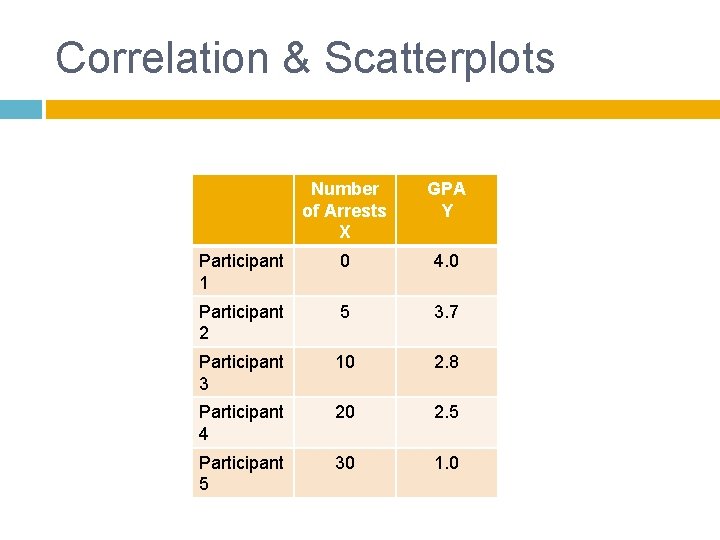
Correlation & Scatterplots Number of Arrests X GPA Y Participant 1 0 4. 0 Participant 2 5 3. 7 Participant 3 10 2. 8 Participant 4 20 2. 5 Participant 5 30 1. 0

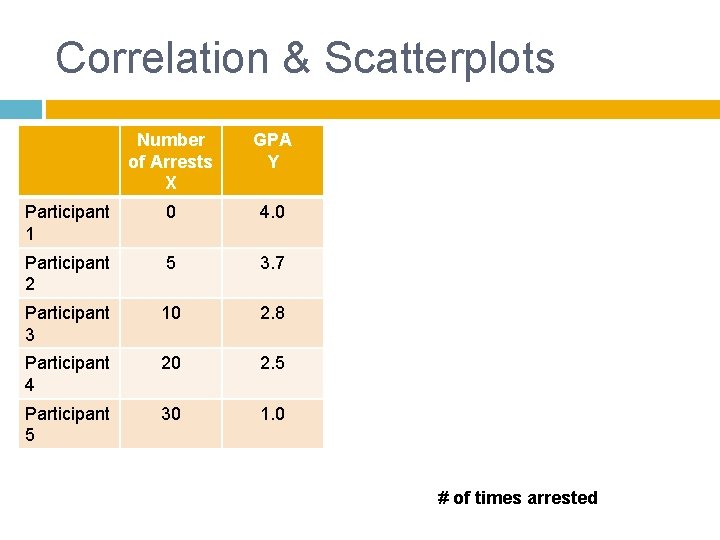
Correlation & Scatterplots Number of Arrests X GPA Y Participant 1 0 4. 0 Participant 2 5 3. 7 Participant 3 10 2. 8 Participant 4 20 2. 5 Participant 5 30 1. 0 # of times arrested

Pearson’s r Formula SP = Sum of products (of deviations) SSx = Sum of Squares of X SSy = Sum of Squares of Y

Pearson’s r Calculating SP � Definitional 1. formula 2. 3. � Computational formula Find X & Y deviations for each individual Find product of deviations for each individual Sum the products

Example #1 Calculating SP – Definitional Formula Step 2: Multiply the deviations from the mean X Y X-MX Y-MY 2 2 2 -3 = -1 2 -4 = -2 (X-MX)(YMY) 2 4 2 -3 = -1 4 -4 = 0 (-1)(-2) = 2 3 3 3 -3 = 0 3 -4 = -1 (-1)(0) = 0 5 7 5 -3 = 2 7 -4 = 3 (0)(-1) = 0 (2)(3) = 6 SX = 12 SY = 16 MX = SX/n = 12/4 = 3 MY = SY/n = 16/4 = 4 Step 1: Find deviations for X and Y separately Step 3: Sum the products

Example #1 Calculating SP – Computational Formula X Y XY 2 2 4 8 3 3 9 5 7 35 SX = 12 SY = 16 MX = SX/n = 12/4 = 3 MY = SY/n = 16/4 = 4

Calculating Pearson’s r 1. Calculate SP 2. Calculate SS for X 3. Calculate SS for Y 4. Plug numbers into formula

Calculating Pearson’s r 1. Calculate SP 2. Calculate SS for X 3. Calculate SS for Y 4. Plug numbers into formula X Y 2 2 2 4 3 3 5 7

Example #1 - Answers Calculating Pearson’s r X Y X-MX Y-MY XY X 2 Y 2 2 -4 = -2 (X-MX)(YMY) 2 2 2 -3 = -1 4 4 4 2 -3 = -1 4 -4 = 0 (-1)(-2) = 2 8 4 16 1 4 3 3 3 -3 = 0 3 -4 = -1 (-1)(0) = 0 9 9 9 1 0 5 7 5 -3 = 2 7 -4 = 3 (0)(-1) = 0 35 25 49 0 1 4 9 SX = 12 SY = 16 MX = SX/n = 12/4 = 3 MY = SY/n = 16/4 = 4 (2)(3) = 6 (X-MX)2 (YMY)2

Pearson’s r r = covariability of X and Y separately

Using Pearson’s r Prediction Validity Reliability

Verbal Descriptions 1) r = -. 84 between total mileage & auto resale value 2) r = -. 35 between the number of days absent from school & performance on a math test 3) r = -. 05 between height & IQ 4) r =. 03 between anxiety level & college GPA 5) r =. 56 between age of schoolchildren & reading comprehension level

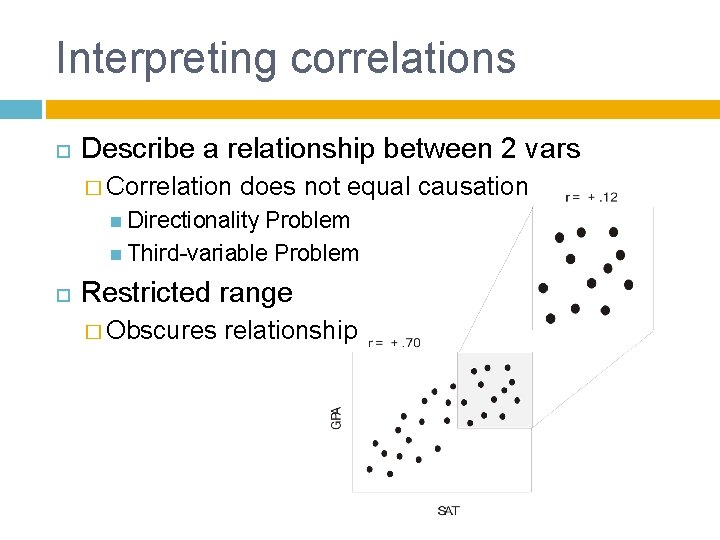
Interpreting correlations Describe a relationship between 2 vars � Correlation does not equal causation Directionality Problem Third-variable Problem Restricted range � Obscures relationship

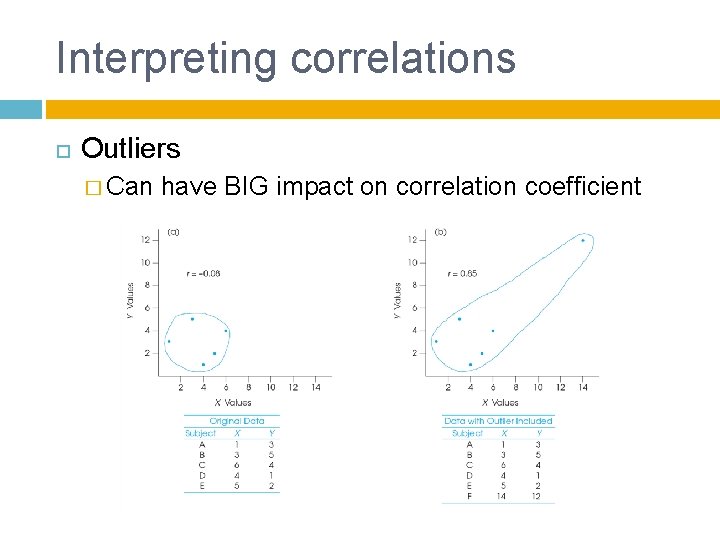
Interpreting correlations Outliers � Can have BIG impact on correlation coefficient

Interpreting correlations Strength & Prediction � Coefficient of determination r 2 Proportion of variability in one variable that can be determined from the relationship w/ the other variable �r =. 60, then r 2 =. 36 or 36% � 36% of the total variability in X is consistently associated with variability in Y � “predicted” and “accounted for” variability

Mini-Review Correlations � Calculation Sum � Using of Pearson’s r of product deviations Pearson’s r � Verbal descriptions � Interpretation of Pearson’s r

Example #2 Practice – Calculate Pearson’s r 1. Calculate SP 2. Calculate SS for X 3. 4. Calculate SS for Y Plug numbers into formula Ex 1 X Y 2 9 1 10 3 6 0 8 4 2

Example #2 X Y X-MX Y-MY 2 9 2 -2 = 0 1 10 3 SP = S(X-MX)(YMY) SS Y XY X 2 Y 2 9 -7 = 2 (X-MX)(YMY) 18 4 81 1 -2 = -1 10 -7 = 3 (0)(2) = 0 10 1 100 0 4 6 3 -2 = 1 6 -7 = -1 (-1)(3) = -3 18 9 36 1 9 0 8 0 -2 = -2 8 -7 = 1 (1)(-1) = -1 0 0 64 1 1 4 2 4 -2 = 2 2 -7 = -5 (-2)(1) = -2 8 16 4 4 1 4 25 (2)(-5) = -10 SX = 10 SY = 35 MX = SX/n = 10/5 = 2 MY = SY/n = 35/5 = 7 (X-MX)2 SS X (YMY)2

Hypothesis Testing Making inferences based on sample information Is it a statistically significant relationship? Or simply chance?

Conceptually - Degrees of freedom Knowing M (the mean) restricts variability in sample Score � 1 score will be dependent on others n = 5, SX = 20 If we know first 3 scores If we know first 4 scores X 1 = 6 X 2 = 4 X 3 = 2 X 4 = 5 X 5 = 3 Σx = 20 With n=5, there can be only 4 df

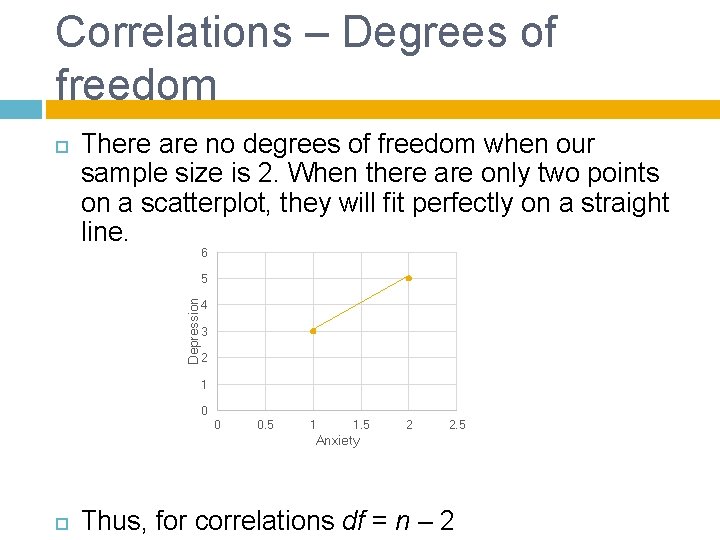
Correlations – Degrees of freedom There are no degrees of freedom when our sample size is 2. When there are only two points on a scatterplot, they will fit perfectly on a straight line. 6 Depression 5 4 3 2 1 0 0 0. 5 1 1. 5 2 2. 5 Anxiety Thus, for correlations df = n – 2

Using table to determine significance Find degrees of freedom � Correlations: df = n – 2 Use level of significance (e. g. , a =. 05) for twotailed test to find column in Table Determine critical value � Value calculated r must equal or exceed to be significant Compare calculated r w/ critical value � If calculated r less than critical value = not significant APA � The correlation between hours watching television and amount of aggression is not significant, r (3) = -. 80, p >. 05. Think about sample size

Spearman correlation Used when: � Ordinal data If 1 variable is on ratio scale, then change scores for that variable into ranks Difference between pair of ranks

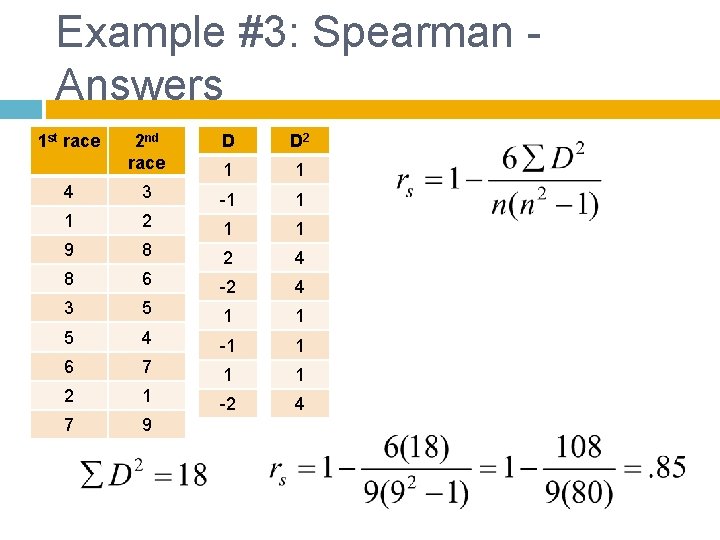
Example #3: Spearman correlation 1 st race 2 nd race 4 3 1 2 9 8 8 6 3 5 5 4 6 7 2 1 7 9

Example #3: Spearman Answers 1 st race 2 nd race D D 2 1 1 4 3 -1 1 1 2 1 1 9 8 2 4 8 6 -2 4 3 5 1 1 5 4 -1 1 6 7 1 1 2 1 -2 4 7 9

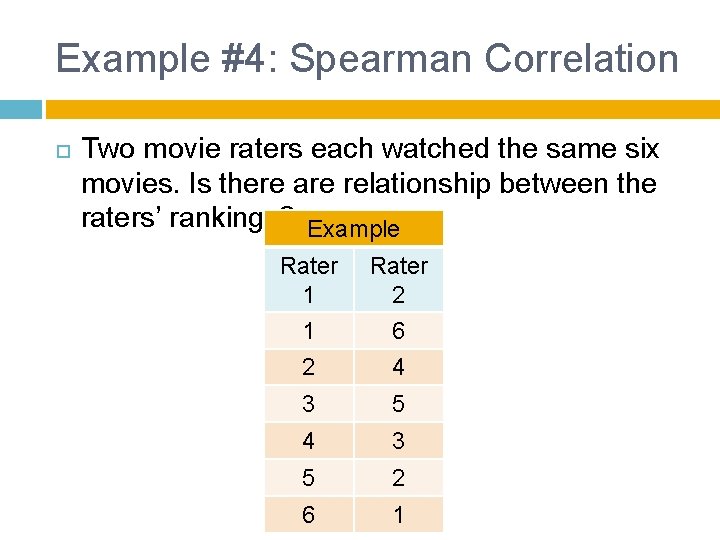
Example #4: Spearman Correlation Two movie raters each watched the same six movies. Is there are relationship between the raters’ rankings? Example Rater 1 1 Rater 2 6 2 4 3 5 2 6 1

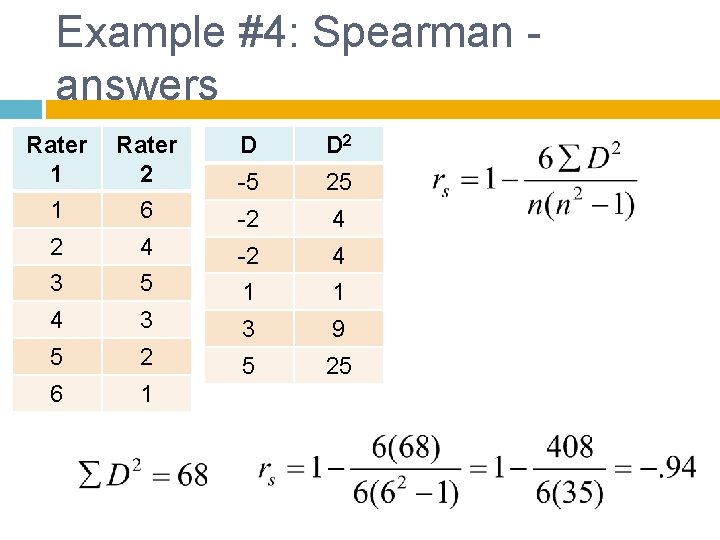
Example #4: Spearman answers Rater 1 Rater 2 D D 2 -5 25 1 6 -2 4 3 5 1 1 4 3 3 9 5 25 6 1

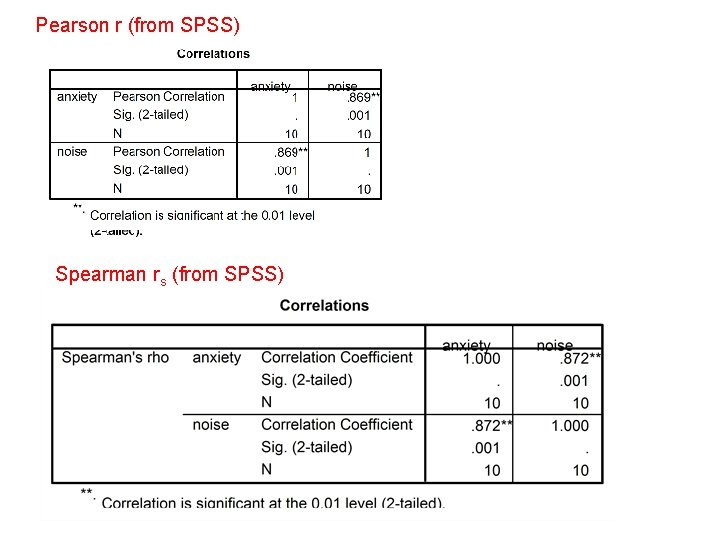
Pearson r (from SPSS) Spearman rs (from SPSS)

Example #5: Pearson’s r 35 Participant (Y) 1 2 3 4 1. 2. 3. 4. Motivation (X) 3 6 9 2 Depression 8 4 2 2 Sketch a scatterplot. Calculate the correlation coefficient. Determine if it is statistically significant at the. 05 level for a 2 -tailed test. Write an APA format conclusion.