GIS SYSTEMY INFORMACJI GEOGRAFICZNEJ ODWZOROWANIA KARTOGRAFICZNE PRZESTRZENIE EUKLIDESOWE

GIS – SYSTEMY INFORMACJI GEOGRAFICZNEJ ODWZOROWANIA KARTOGRAFICZNE, PRZESTRZENIE EUKLIDESOWE, OTOCZKA WYPUKŁA, REPREZENTACJE KRZYWYCH, OPTYMALIZACJE

ZAGADNIENIA 1. 2. 3. 4. 5. 6. 7. Właściwości odwzorowań kartograficznych Systemy odniesień kartograficznych Układ 1942, Układ 1965, Układ 1992, Układ 2000 Układy wysokości Podstawowe definicje – iloczyn skalarny, wektorowy Obliczanie powierzchni wieloboków Algorytm znajdowania otoczki wypukłej

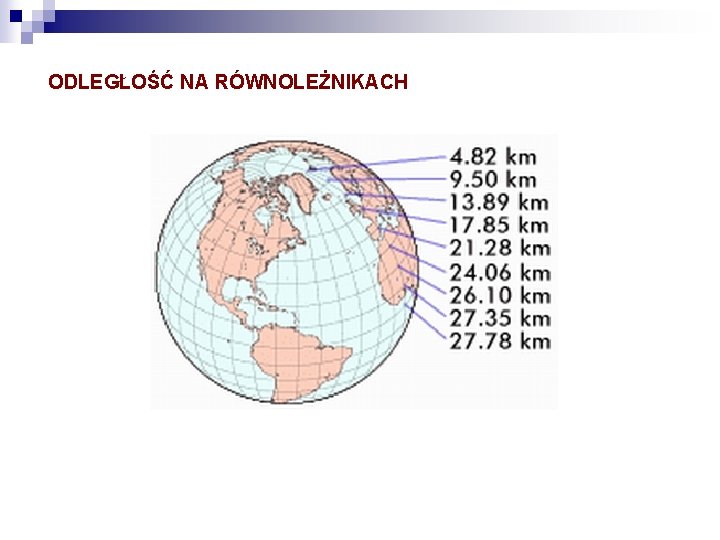
ODLEGŁOŚĆ NA RÓWNOLEŻNIKACH

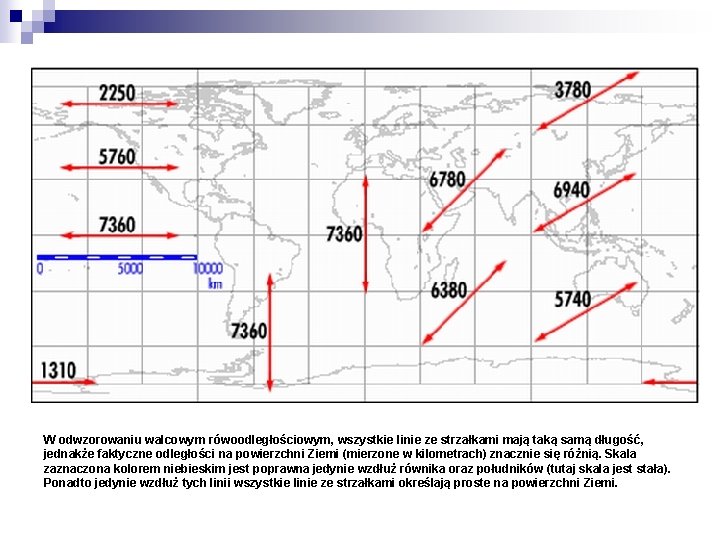
W odwzorowaniu walcowym rówoodległościowym, wszystkie linie ze strzałkami mają taką samą długość, jednakże faktyczne odległości na powierzchni Ziemi (mierzone w kilometrach) znacznie się różnią. Skala zaznaczona kolorem niebieskim jest poprawna jedynie wzdłuż równika oraz południków (tutaj skala jest stała). Ponadto jedynie wzdłuż tych linii wszystkie linie ze strzałkami określają proste na powierzchni Ziemi.

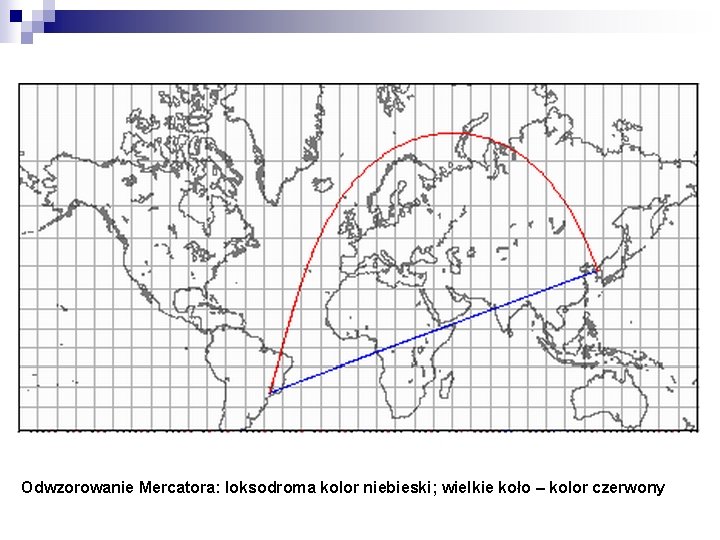
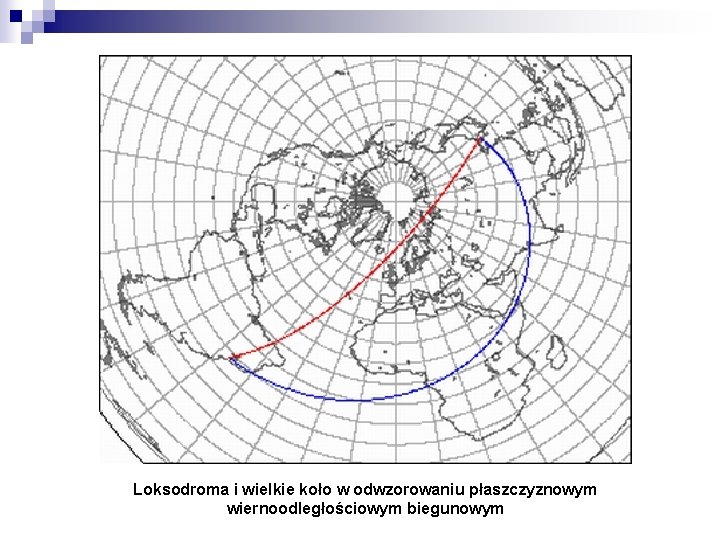
ODWZOROWANIE WIERNOKĄTNE Odwzorowanie równokątne lokalnie zachowuje kąty. W ten sposób, dowolne dwie linie na mapie mają taki sam kąt jaki mają faktycznie na powierzchni Ziemi. W szczególności, siatka kartograficzna – południki i równoleżniki zawsze przecinają się pod kątem prostym (warunek konieczny, ale nie wystarczający). W dowolnym punkcie, skala jest taka sama we wszystkich kierunkach. Kształt nie jest zachowany, ponieważ odwzorowanie równokątne zniekształca skalę – skala nie jest wszędzie taka sama). Odwzorowanie płaszczyznowe stereograficzne oraz Merkatora jest wiernokątne.

Odwzorowanie Mercatora: loksodroma kolor niebieski; wielkie koło – kolor czerwony

Loksodroma i wielkie koło w odwzorowaniu płaszczyznowym wiernoodległościowym biegunowym

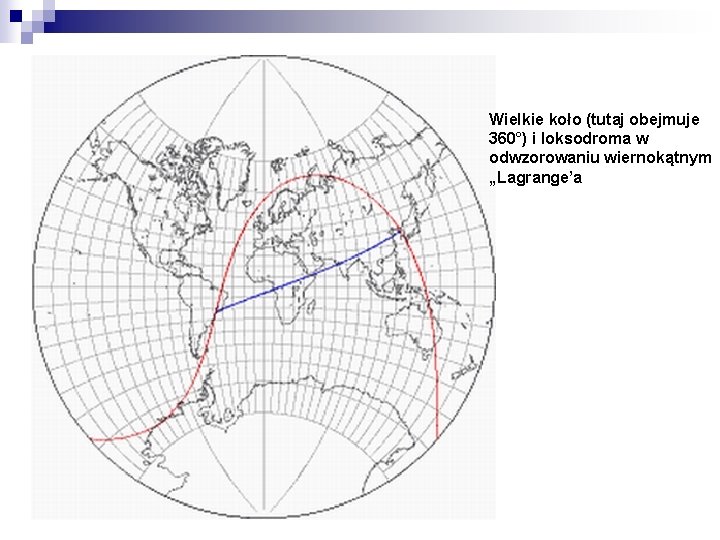
Wielkie koło (tutaj obejmuje 360°) i loksodroma w odwzorowaniu wiernokątnym „Lagrange’a

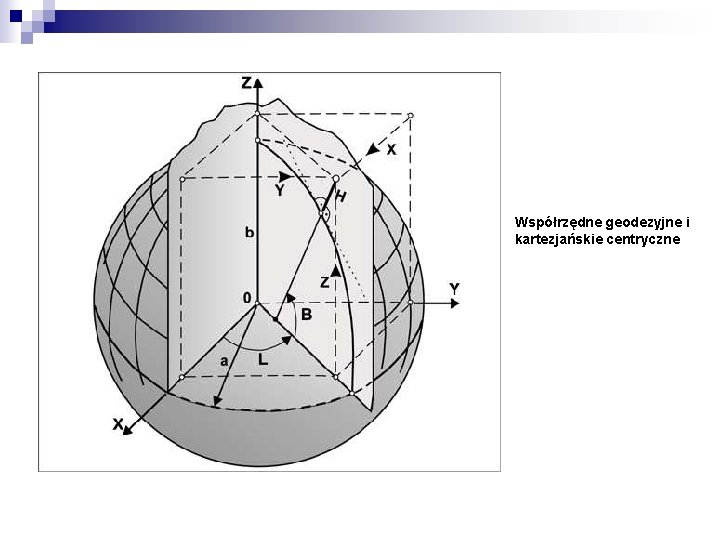
Współrzędne geodezyjne i kartezjańskie centryczne

PRZELICZANIE WSPÓŁRZĘDNYCH KARTOGRAFICZNYCH NA ELIPSOIDALNE

PODSTAWOWE WIELKOŚCI

UKŁADY GEODEZYJNE W POLSCE ITRS i ETRS ITRS (ang. International Terrestrial Reference System) oraz ETRS (ang. European Terrestrial Reference System) są skróconymi nazwami odpowiednio: globalnego (międzynarodowego) i europejskiego (jako podsystemu kontynentalnego) systemu odniesień przestrzennych. Samo pojęcie systemu ma charakter bardzo ogólny. Obejmuje on zarówno definicję układu współrzędnych w ujęciu teoretycznym i aplikacyjnym (definicję układu odniesienia), jak też całą strukturę organizacyjno techniczną i naukową związaną z realizacją tego układu, jego funkcjonowaniem i permanentną kontrolą

UKŁADY GEODEZYJNE W POLSCE ITRF i ETRF Praktyczną (fizyczną) realizacją (aplikacją) układu współrzędnych w systemie ITRS / ETRS jest układ odniesienia ITRF / ETRF (ang. International / European Reference Frame lub krócej: European Frame - EUREF) tworzony fizycznie przez sieć stacji obserwacyjnych, rozlokowanych w stabilnych tektonicznie rejonach świata i kontynentu. Układ odniesienia w rozumieniu zbioru punktów powiązanych z Ziemi, jest obiektem dynamicznym, poddanym permanentnym obserwacjom. Stanom quasi-statycznym (epokowym) sieci stacji ITRF / ETRF przypisuje się indeks epoki obserwacyjnej. Celem ujednolicenia pomiarów geodezyjnych, obserwacje aktualne, dotyczące wyznaczeń położeń punktów, redukuje się do umownego stanu początkowego. W Polsce, obowiązuje redukcja pomiarów poziomych do epoki '89 (ETRF'89). Państwowe osnowy geodezyjne, poziome i trójwymiarowe (EUREF-POL + POLREF) są nawiązane do punktów sieci europejskiej w układzie ETRF'89.

W zastosowaniach kartograficznych i geodezyjnych są używane trzy różne powierzchnie: - naturalna fizyczna powierzchnia ziemi, - elipsoida odniesienia, - powierzchnia o jednakowym potencjale, zwana geoidą.

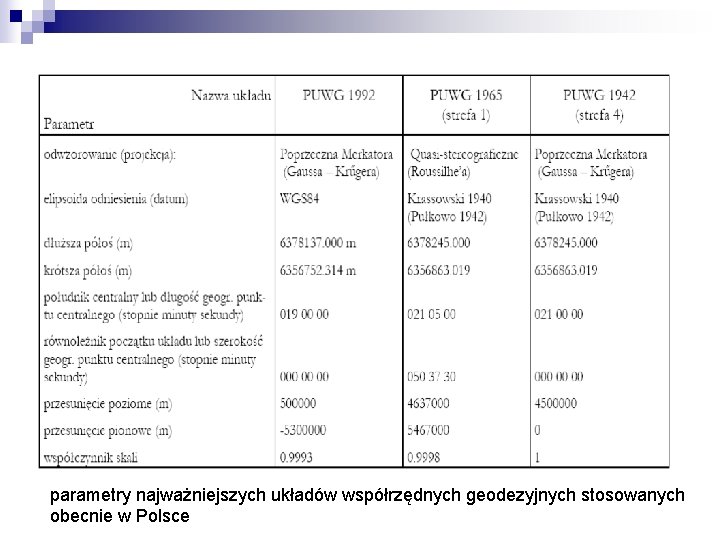
parametry najważniejszych układów współrzędnych geodezyjnych stosowanych obecnie w Polsce

ODWZOROWANIA UŻYWANE W POLSCE Mercatora (M - Mercator Projection) - odwzorowanie normalne walcowe wiernokątne elipsoidy - walec jest styczny w równiku. • • Uniwersalne poprzeczne Mercatora (UTM - Universal Transversal Mercator) odwzorowanie poprzeczne walcowe wiernokątne - walec sieczny do elipsoidy symetralnie do południka osiowego danej strefy. • Gaussa-Krügera - odwzorowanie walcowe poprzeczne wiernokątne elipsoidy walec styczny w południku osiowym danej strefy. • W Polsce obecnie jest używane odwzorowanie płaszczyznowe quasistereograficzne wiernokątne elipsoidy na płaszczyznę (w czterech strefach odwzorowawczych) zwane popularnie odwzorowaniem '65

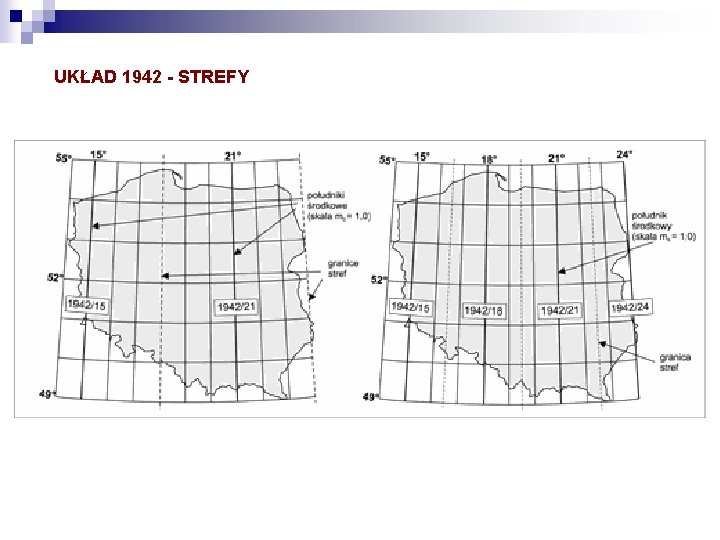
UKŁAD 1942 Do połowy lat 60. obowiązywał w Polsce układ współrzędnych zwany "1942" (od daty wprowadzenia systemu elipsoidalnego). Układ ten powstał w wyniku zastosowania odwzorowania Gaussa-Krügera na elipsoidzie Krasowskiego, przy czym obejmował dwa podsystemy: • odwzorowanie w pasach południkowych o szerokości 6°. W wyniku tego na obszarze Polski powstały dwie strefy odwzorowawcze: z południkami środkowymi 15° i 21°; nazywamy je pomocniczo: 1942/15 (6) i 1942/21 (6). Odwzorowanie to miało zastosowanie dla map średnio- i małoskalowych (skale mniejsze od 1: 5000). Zniekształcenia odwzorowawcze zmieniały się od 0 (na południku środkowym każdej strefy) do ok. + 59 cm/km (na brzegach strefy) • odwzorowanie w pasach południkowych o szerokości 3°. W wyniku tego na obszarze Polski powstały cztery strefy odwzorowawcze: z południkami środkowymi 15°, 18°, 21°, 24°; oznaczamy je pomocniczo: 1942/15 (3), 1942/18 (3), 1942/21 (3), 1942/24 (3). Odwzorowanie to miało zastosowanie dla map wielkoskalowych (skala 1: 5000 i większe). Zniekształcenia odwzorowawcze na brzegach stref dochodziły do +15 cm/km.

UKŁAD 1942 - STREFY

UKŁAD "1965" i GUGi. K-80 Od końca lat 60. w służbie cywilnej zaczęto wprowadzać nowy, 5 -strefowy układ odwzorowawczy (oparty na tym samym systemie elipsoidalnym) zwany krótko układem "1965". Kraj został podzielony na pięć stref , przy czym w strefach 1, 2, 3, 4 zastosowano tzw. odwzorowanie quasi-stereograficzne (Roussilhe projection), natomiast w strefie 5 zmodyfikowane odwzorowanie Gaussa-Krügera. Każde odwzorowanie quasi-stereograficzne jako wiernokątne odwzorowanie płaszczyznowe elipsoidy definiuje się, określając położenie punktu głównego (punktu styczności płaszczyzny z powierzchnią elipsoidy) oraz skalę odwzorowania w tym punkcie, będącą równocześnie skalą podobieństwa odwzorowania. W strefach 1 -4 układu "1965" przyjęto skalę w punkcie głównym m 0 = 0, 9998, tzn. zniekształcenie odwzorowawcze w tym punkcie wynosiło z założenia 20 cm/km. Układ "1965" był przeznaczony głównie do tworzenia i eksploatacji mapy zasadniczej.

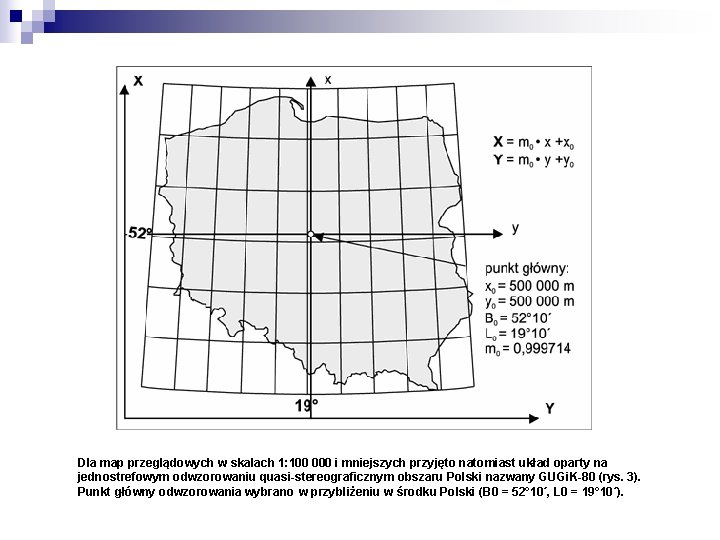
Odwzorowanie quasi-stereograficzne równokątne elipsoidy obrotowej Odwzorowanie tego typu było stosowane na mapach wojskowych w Polsce przed II Wojną Światową. Jest to odwzorowanie elipsoidy na płaszczyznę - najlepiej pasuje do obszarów zbliżonych kształtem do kwadratu. W Polsce po wojnie zastosowano tego typu odwzorowanie przy tworzeniu układu współrzędnych "GUGIK'80". Układ ten wprowadzono w celu opracowania map w skalach 1 : 25 000 i mniejszych pokrywających cały obszar kraju. W odwzorowaniu punktem głównym jest punkt o współrzędnych B 0 = 520 10' , L 0 = 190 10'. Początek układu współrzędnych prostokątnych płaskich x, y pokrywa się z obrazem punktu głównego, a oś x jest skierowana na północ (pokrywa się z obrazem południka osiowego). Skalę długości w punkcie głównym przyjęto równą 0. 999714285. Redukcje długości wynoszą od -20 cm/1 km w okolicy Świnoujścia do +90 cm/1 km w okolicy Leska. W celu wycofania z użytku w resortach cywilnych współrzędnych układu "42" (odwzorowanie Gaussa-Krügera elipsoidy Krasowskiego) zdecydowano się na wprowadzenie układu, zapewniającego służbom geodezyjnym odpowiednie dokładności - układ nazwano "65". Za podstawę opracowania przyjęto teorię prof. Lucjana Grabowskiego z Politechniki Lwowskiej.

REALIZACJA UKŁADU WSPÓŁRZĘDNYCH „ 1965” I GUGIK-80

ZASADA ODWZOROWANIA POŁUDNIKA ŚRODKOWEGO

Dla map przeglądowych w skalach 1: 100 000 i mniejszych przyjęto natomiast układ oparty na jednostrefowym odwzorowaniu quasi-stereograficznym obszaru Polski nazwany GUGi. K-80 (rys. 3). Punkt główny odwzorowania wybrano w przybliżeniu w środku Polski (B 0 = 52° 10´, L 0 = 19° 10´).

ODWZOROWANIA OPARTE NA ELIPSOIDZIE WGS-84 (GRS-80) Od początku lat 90. podjęto prace mające na celu włączenie obszaru Polski do europejskiego systemu odniesień przestrzennych ETRS (European Terrestrial Reference System), będącego częścią światowego systemu ITRS, a reprezentowanego przez układ 35 stacji bazowych, zwany w skrócie ETRF lub EUREF (European Terrestrial Reference Frame). Na obszarze Polski utworzono najpierw sieć EUREF-POL złożoną z 11 punktów bazowych, którą następnie zagęszczono siecią ok. 350 punktów, zwaną w skrócie POLREF. Wszystkie pomiary wykonane zostały techniką GPS (Global Positioning System). Sieci EUREF-POL i POLREF stały się z kolei podstawą ponownego wyrównania dawnej sieci astronomiczno-geodezyjnej i triangulacji wypełniającej (sieci I klasy), a następnie także sieci poziomej II klasy. Wszystkie obliczenia wykonano już na nowej elipsoidzie systemu EUREF zwanej w skrócie GRS-80. Nazwa pełna "Geodetic Reference System 1980" dotyczy w istocie szerszego zbioru parametrów geometryczno-fizycznych opisujących Ziemię. W latach późniejszych wprowadzono zmodyfikowany zbiór parametrów znany pod nazwą WGS-84 (World Geodetic System 1984), który praktycznie zmieniał geometrii elipsoidy. Dlatego zamiast nazwy elipsoida (lub układ elipsoidalny) GRS-80 notujemy też równoważnie: WGS-84.

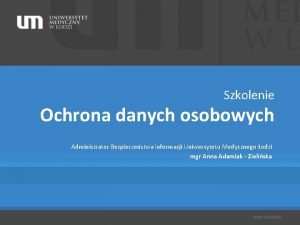
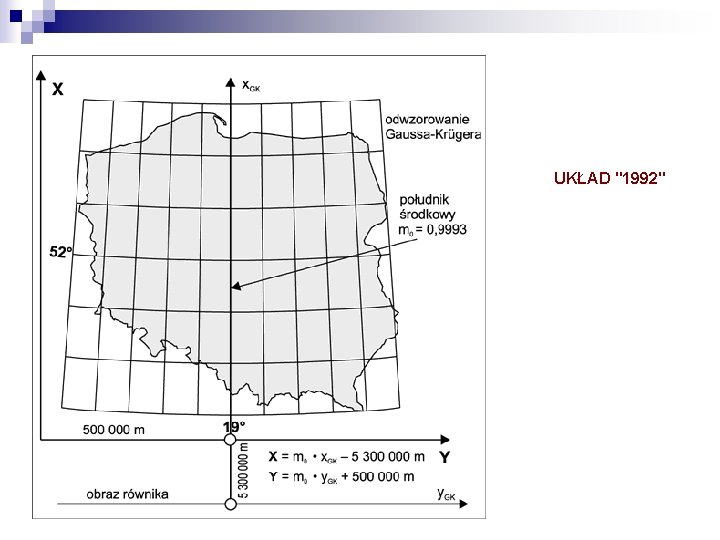
UKŁAD "1992" Zarówno dla osnów poziomych, jak i opracowań kartograficznych przyjęto dwa nowe systemy odwzorowawcze elipsoidy GRS-80: • jednostrefowe dla obszaru Polski odwzorowanie Gaussa-Krügera z południkiem środkowym L 0 = 19° i skalą podobieństwa m 0 = 0, 9993 (ostatnie założenie ma na celu równomierny rozkład zniekształceń liniowych, od 70 cm/km na południku środkowym do ok. +90 cm/km w skrajnych, wschodnich obszarach Polski). Układ został nazwany skrótowo "1992". Obecnie stanowi podstawę do wykonywania nowych map w skalach 1: 10 000 i mniejszych. Ze względu na znaczne zniekształcenia liniowe układ nie jest rekomendowany do wielkoskalowych opracowań kartograficznych;

UKŁAD "1992"

Izolinie zniekształceń elementarnych [cm/km] w układzie "1992"

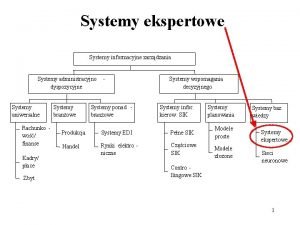
UKŁAD "2000" Czterostrefowe odwzorowanie Gaussa-Krügera elipsoidy GRS-80 w pasach 3 -stopniowych, zwane skrótowo układem "2000". W tym przypadku koncepcja nawiązuje do dawnego układu "1942". Różnica polega jednak na odmienności przyjętych elipsoid odniesienia oraz na zastosowaniu dodatkowej skali podobieństwa (skali kurczenia na południku środkowym). W układzie "2000" zastosowano skalę m 0 = 0, 999923, która realizuje kompromis w rozłożeniu zniekształceń liniowych (od � 7, 7 cm/km na południku środkowym strefy do maksymalnie ok. +7 cm/km na brzegu strefy). Ograniczając się do powyższej listy najważniejszych praktycznie układów, należy stwierdzić, że za wyjątkiem "1965" (w strefach 1 -4) oraz GUGi. K-80 wszystkie pozostałe układy, wywodzące się z elipsoidy GRS-80 lub Krasowskiego, powstały jako aplikacje odwzorowania Gaussa-Krügera. Procedura realizacji tego odwzorowania stanowić będzie zatem istotny element procesu przeliczeń współrzędnych pomiędzy różnymi układami. Przyjęcie odwzorowania Gaussa-Krügera jako podstawy nowych definicji państwowych układów współrzędnych, np. jednolitego układu "1992", ma swoją genezę w tradycji europejskiej (zwłaszcza niemieckiej).

Izolinie zniekształceń elementarnych [cm/km] w układzie PUK 2000 (odwzorowanie analityczne wiernokątne), © INFOPRO S. A. w Warszawie

UKŁADY KARTOGRAFICZNE ODZWZOROWANIE GAUSSA-KRUGERA i MERCATORA Odwzorowania Gaussa - Krügera i Mercatora są oparte o te same zasady matematyczne. Różnice we współrzędnych pochodzą od inaczej przyjmowanego współczynnika skali: • w odwzorowaniu Gaussa wiernie odtwarza się południk osiowy; zniekształcenie długości rośnie na zewnątrz, osiągając maksimum na skraju strefy (dla strefy sześciostopniowej zniekształcenie długości wynosi 67 cm na 1 km długości) • w odwzorowaniu UTM współczynnik skali południka środkowego wynosi 0. 9996, na siecznych almukantaratach jest równy 1. 0000 i wzrasta w kierunku skraju strefy do 1. 0016 (dla pasów sześciostopniowych). W odwzorowaniu UTM zniekształcenia odległości są mniejsze i bardziej równomiernie rozłożone, a zatem powierzchnia elipsoidy jest wierniej odwzorowana na płaszczyźnie niż w odwzorowaniu Gaussa. Współczynnik skali jest prosty w stosowaniu, należy mnożyć przez niego obliczone w odwzorowaniu współrzędne x 0 = x * m, y 0 = y * m

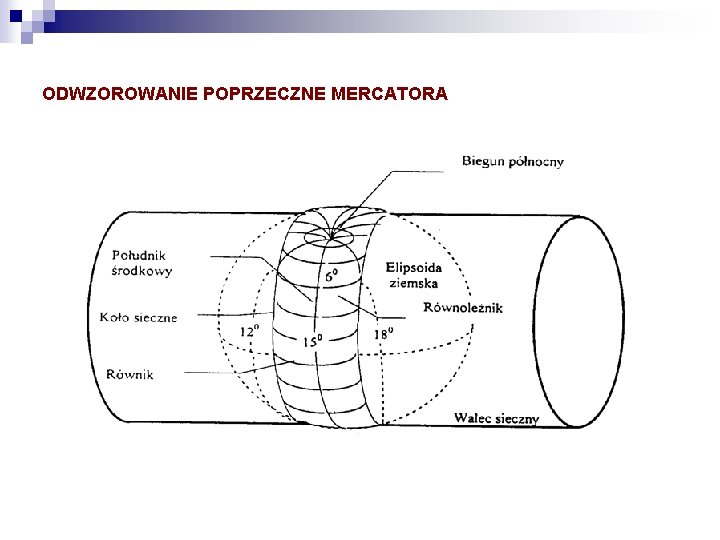
ODWZOROWANIE POPRZECZNE MERCATORA

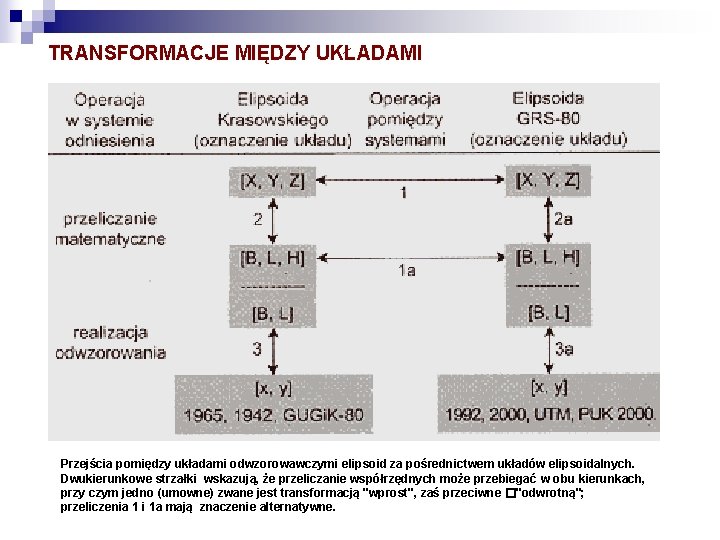
TRANSFORMACJE MIĘDZY UKŁADAMI Przejścia pomiędzy układami odwzorowawczymi elipsoid za pośrednictwem układów elipsoidalnych. Dwukierunkowe strzałki wskazują, że przeliczanie współrzędnych może przebiegać w obu kierunkach, przy czym jedno (umowne) zwane jest transformacją "wprost", zaś przeciwne �"odwrotną"; przeliczenia 1 i 1 a mają znaczenie alternatywne.

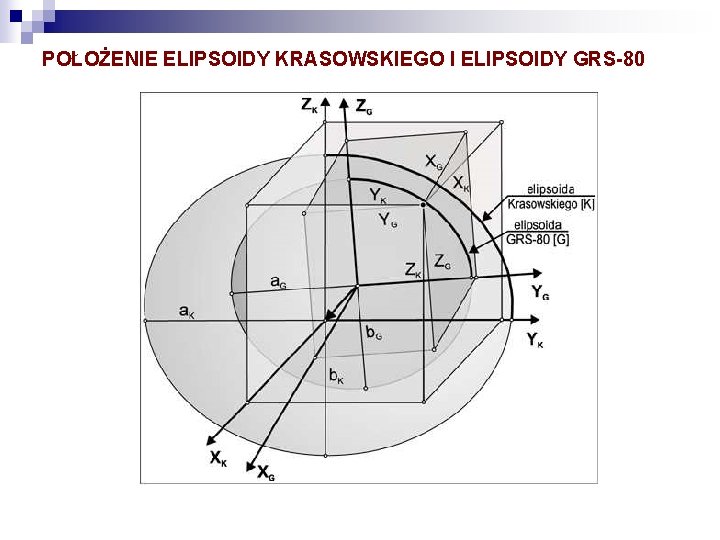
POŁOŻENIE ELIPSOIDY KRASOWSKIEGO I ELIPSOIDY GRS-80

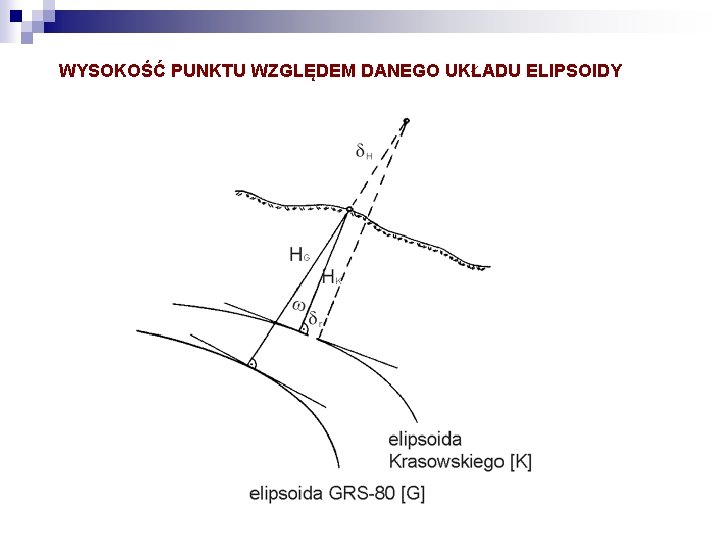
ZAMIANA WSPÓŁRZĘDNYCH Z JEDNEGO UKŁADU NA INNY UKŁAD Operacje przejścia z jednego układu do drugiego odbywa się za pośrednictwem ściśle określonych funkcji transformacyjnych (odwzorowawczych) i ich parametrów liczbowych. Powstaje praktyczne pytanie, czy można bezpośrednio przeliczyć współrzędne płaskie, na przykład z układu "1965" do układu "1992", poprzez zastosowanie odpowiednich przekształceń dwuwymiarowych. Wbrew temu, co sugeruje się niekiedy w praktyce, przeliczenie takie nie jest formalnie poprawne bez udziału przynajmniej przybliżonej informacji o wysokości elipsoidalnej punktu w systemie, z którego wychodzimy (aby przejść pomiędzy systemami, należy do współrzędnych B, L dołączyć wysokość elipsoidalną H). Zmiana wysokości punktu wpływa na zmianę jego położenia poziomego przy przejściu z jednej elipsoidy na drugą. Załóżmy, że wysokość została określona z pewnym błędem d. H i oszacujmy, jak wielce błąd ten wpływa na transformowane współrzędne płaskie. Z informacji o wzajemnym położeniu elipsoid wynika, że maksymalna kątowa rozwartość normalnych (poprowadzonych z tego samego punktu na powierzchni Ziemi do obu elipsoid) ma wartość rzędu 7˝.

WYSOKOŚĆ PUNKTU WZGLĘDEM DANEGO UKŁADU ELIPSOIDY

ELIPSOIDY W POLSKICH UKŁADACH WSPÓŁRZĘDNYCH

UKŁAD WSPÓŁRZĘDNYCH 2000

PRZELICZENIE WSPÓŁRZĘDNYCH GAUSSA-KRUGERA NA WSPÓŁRZĘDNE 2000

ZASADA APLIKACJI ODWZOROWANIA GAUSSA-KRUGERA

ODWZOROWANIE GAUSSA-KRUGERA

CHARAKTERYSTYKA UKŁADU WGS 84

ELIPSOIDA WGS 84 Przy wyborze elipsoidy odniesienia dla systemu WGS 84 kierowano się zaleceniami Międzynarodowej Unii Geodezji i Geofizyki, dotyczącymi światowej elipsoidy odniesienia o określonych parametrach (GRS 80 - Geodetic Reference System 1980). Dlatego też przyjęto identyczne parametry dla elipsoidy WGS 84 co parametry elipsoidy GRS 80, z jedną małą zmianą. Dotyczy ona harmoniki zonalnej drugiego rzędu J 2. Zdefiniowane parametry elipsoidy WGS 84:

LOKALNE UKŁADY ODNIESIENIA STOSOWANE W POLSCE A UKŁAD WGS 84

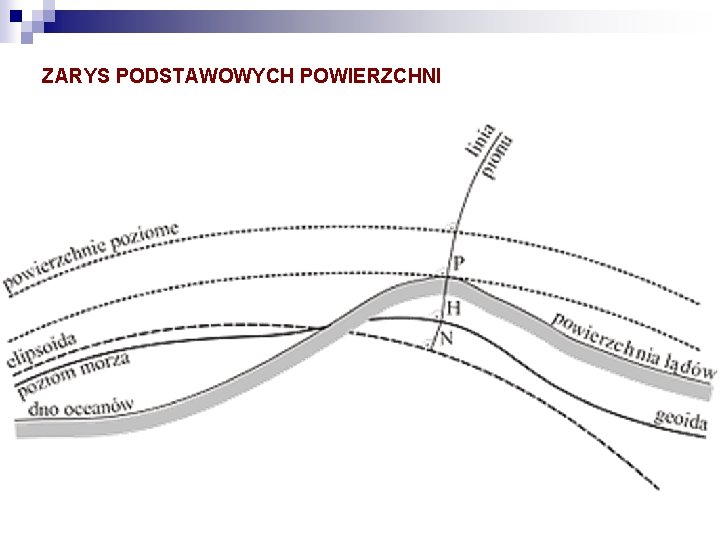
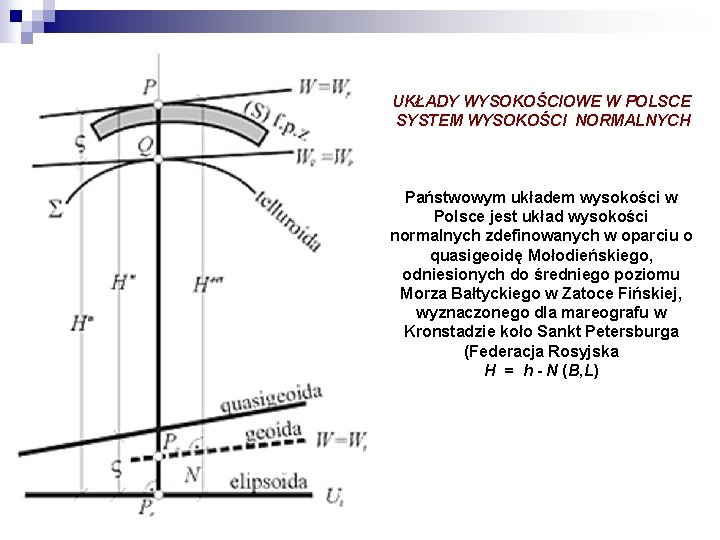
UKŁADY WYSOKOŚCIOWE W POLSCE GEOIDA - teoretyczna powierzchnia stałego potencjału siły ciężkości, pokrywająca się z powierzchnią mórz i oceanów Ziemi, przedłużona umownie pod lądami. Kierunek siły ciężkości jest prostopadły do powierzchni geoidy w każdym jej punkcie. Kształt geoidy jest zbliżony do elipsoidy obrotowej, a maksymalne odchylenia od elipsoidy ziemskiej (GRS'80) są rzędu 100 m (na terenach Polski od 28 do 43 metrów). Wyznacza się ją na podstawie pomiarów astronomiczno-geodezyjnych, satelitarnych (altimetria satelitarna), grawimetrycznych i niwelacyjnych

ZARYS PODSTAWOWYCH POWIERZCHNI

UKŁADY WYSOKOŚCIOWE W POLSCE SYSTEM WYSOKOŚCI NORMALNYCH Państwowym układem wysokości w Polsce jest układ wysokości normalnych zdefinowanych w oparciu o quasigeoidę Mołodieńskiego, odniesionych do średniego poziomu Morza Bałtyckiego w Zatoce Fińskiej, wyznaczonego dla mareografu w Kronstadzie koło Sankt Petersburga (Federacja Rosyjska H = h - N (B, L)

OKREŚLENIE WYSOKOŚCI Problem określenia wysokości jest odrębnym problemem, wymagającym znajomości odstępów geoidy od elipsoidy WGS 84 w danym rejonie. Dokładna mapa takich odstępów zwana mapą geoidy została dla obszaru Polski opracowana w Centrum Badań Kosmicznych PAN przez prof. Adama Łyszkowicza. Posiadając mapę geoidy (w zapisie cyfrowym) można określić odstęp geoidy w dowolnym, o znanych współrzędnych punkcie z dokładnością lepszą od 5 cm. Wówczas: H = h + N, lub h = H - N, gdzie: N - wysokość nad elipsoidą WGS 84, H - wysokość określana jako wysokość nad powierzchnią morza. Na obszarze Polski odstępy elipsoidy satelitarnej WGS 84 od geoidy sięgają od 26 m do 43 m.

OSNOWA GEODEZYJNA - DEFINICJA Osnowę geodezyjną stanowi uporządkowany zbiór punktów geodezyjnych, dla których zostało określone wzajemne położenie względem przyjętego układu odniesienia. Osnowa pozioma może być udostępniana w wybranym układzie: 2000, 1992, 1965, długość i szerokość geodezyjna geograficzna (B, L)

SIATKA KARTOGRAFICZNA - DEFINICJA Obraz kartograficzny tworzą elementy treści mapy (właściwy model przestrzeni zapisany w sposób znakowy) oraz elementy związane z matematyczną konstrukcją mapy, takie jak: punkty osnowy geodezyjnej, siatka kartograficzna – obraz południków i równoleżników elipsoidy w przyjętym odwzorowaniu, siatka kilometrowa – układ linii równoległych do kartezjańskiego układu współrzędnych (X, Y) związanego z płaszczyzną obrazu.

PODSTAWOWE POJĘCIA GEOMETRII OBLICZENIOWEJ Pojęcie przestrzeni wektorowej Pojęcie punktu w przestrzeni wektorowej Pojęcie metryki – odległości między dwoma punktami przestrzeni wektorowej Pojęcie normy – czyli długości wektora w przestrzeni wektorowej Pojęcie iloczynu skalarnego wektorów Pojęcie Iloczynu wektorowego

ILOCZYN SKALARNY WEKTORÓW WŁAŚCIWOŚCI ILOCZYNU SKALARNEGO:

ILOCZYN WEKTOROWY WŁAŚCIOWŚCI ILOCZYNU WEKTOROWEGO

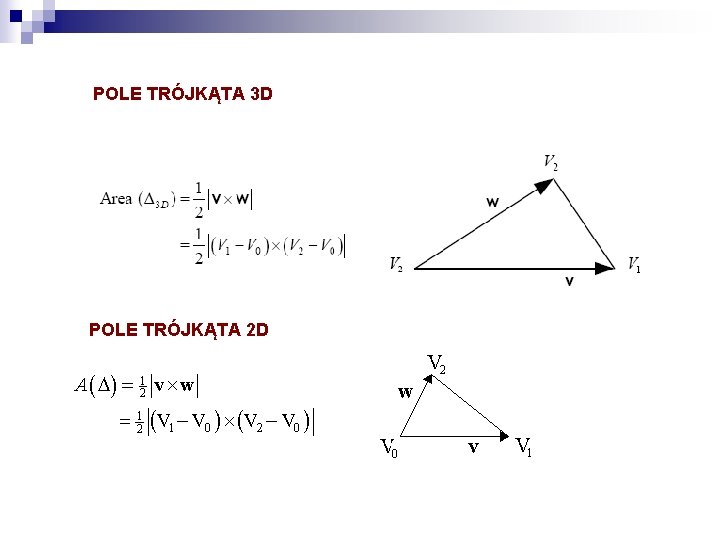
POLE TRÓJKĄTA 3 D POLE TRÓJKĄTA 2 D

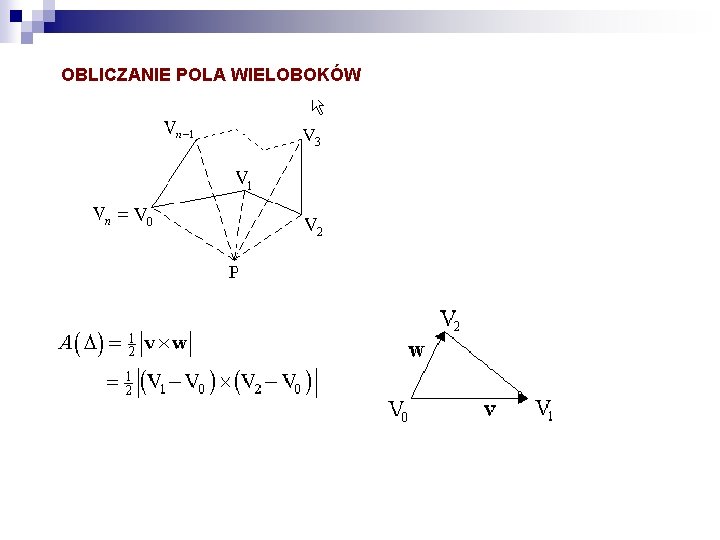
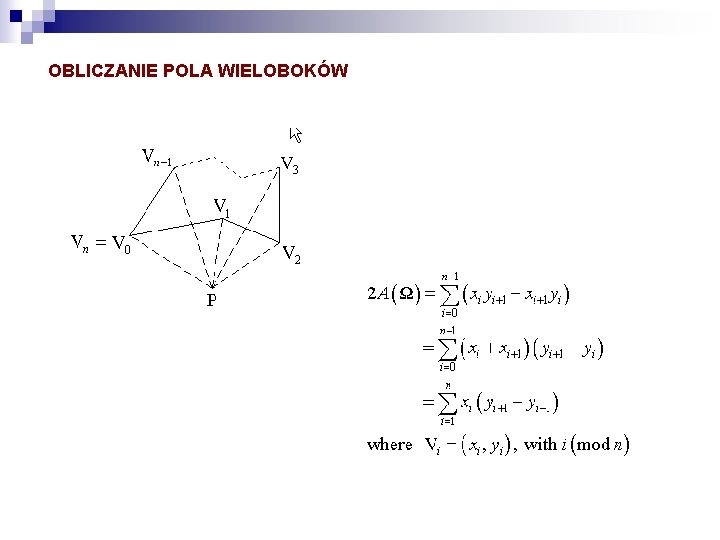
OBLICZANIE POLA WIELOBOKÓW

OBLICZANIE POLA WIELOBOKÓW

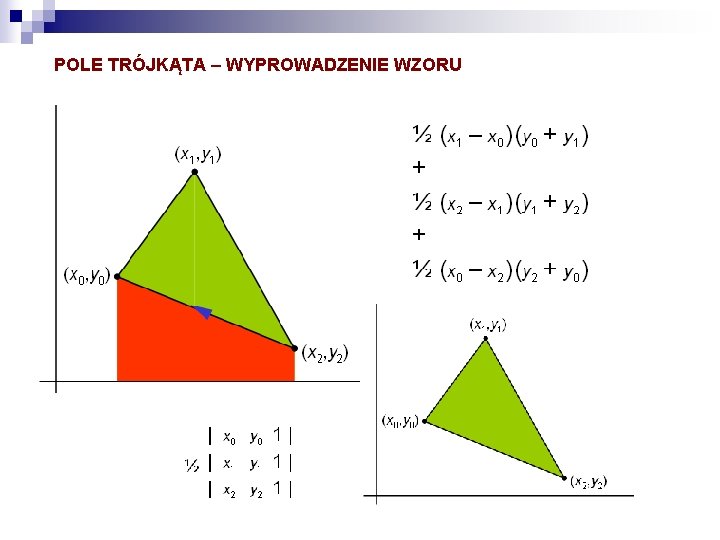
POLE TRÓJKĄTA – WYPROWADZENIE WZORU

WYPUKŁA OTOCZKA ZBIORU PUNKTÓW Q to najmniejszy wypukły wielokąt taki, że każdy punkt ze zbioru Q leży albo na brzegu wielokąta albo w jego wnętrzu. Otoczka składa się z 6 wierzchołków, jest to najmniejszy podzbiór zbioru Q taki że ich ciąg tworzy otoczkę zbioru Q.

ALGORYTM GRAHAMA ZNAJDOWANIA OTOCZKI WYPUKŁEJ 1. 2. 3. 4. 5. 6. Wybierz dolowlny punkt (ozn. O) należący do otoczki wypukłej punktów (najczęściej jest to centroid). Przesuń wszystkie punkty tak, by punkt O pokrył się z początkiem układu współrzędnych. Posortuj punkty leksykograficznie względem: kąta pomiędzy wektorem OPi a dodatnią osią układu współrzędnych, oraz odległości punktu Pi od początku układu współrzędnych. Wybierz punkt (ozn. S) o najmniejszej współrzędnej y; jeśli kilka punktów ma tę samą współrzędną y, to wybierz spośród nich punkt o najmniejszej współrzędnej x. Przeglądaj listę posortowanych punktów poczynając od punktu S: Od bieżącej pozycji weź trzy kolejne punkty (ozn. A, B, C): 1. Jeśli punkt B leży na zewnątrz trójkąta AOC, to należy do otoczki wypukłej. Przejdź do następnego punktu na liście. 2. Jeśli punkt B leży wewnątrz trójkąta AOC, to znaczy, że punkt ten nie należy do otoczki. Usuń punkt B z listy i cofnij się o jedną pozycję (o ile bieżąca pozycja jest różna od początkowej).

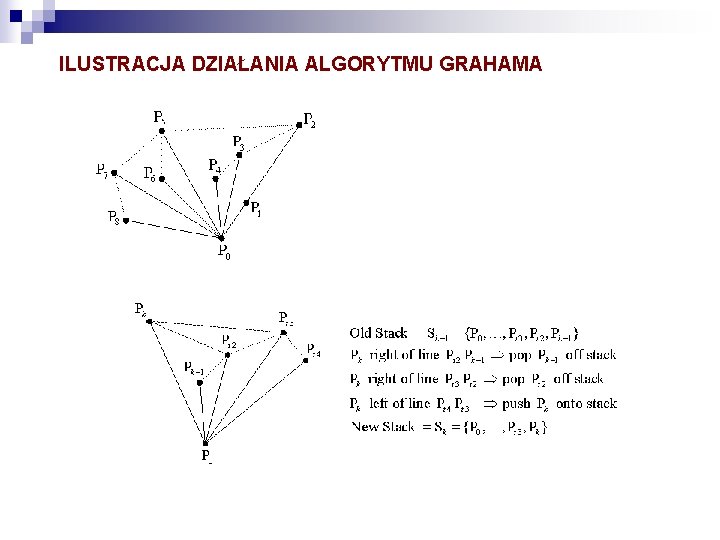
ILUSTRACJA DZIAŁANIA ALGORYTMU GRAHAMA

POŁOŻENIE PUNKTU WZGLĘDEM PROSTEJ is. Left() sprawdzenie po której stronie prostej P 0 -P 1 znajduje się punkt P 2 Return: >0 gdy P 2 po stronie lewej linii P 0 - P 1 =0 gdy P 2 na linii P 0 - P 1 <0 gdy 2 po stronie prawej linii P 0 – P 1 int is. Left( Point P 0, Point P 1, Point P 2 ) { return ( (P 1. x - P 0. x) * (P 2. y - P 0. y) - (P 2. x - P 0. x) * (P 1. y - P 0. y) ); }

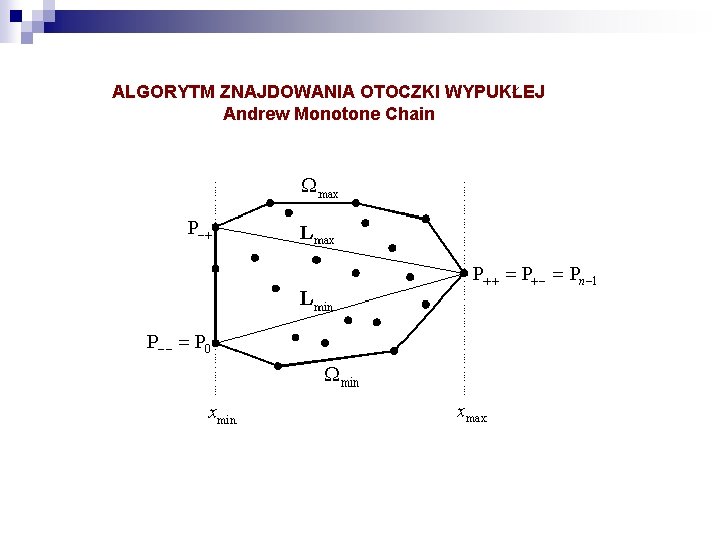
ALGORYTM ZNAJDOWANIA OTOCZKI WYPUKŁEJ Andrew Monotone Chain

PSEUDOKOD ALGORYTMU Andrew Monotone Chain

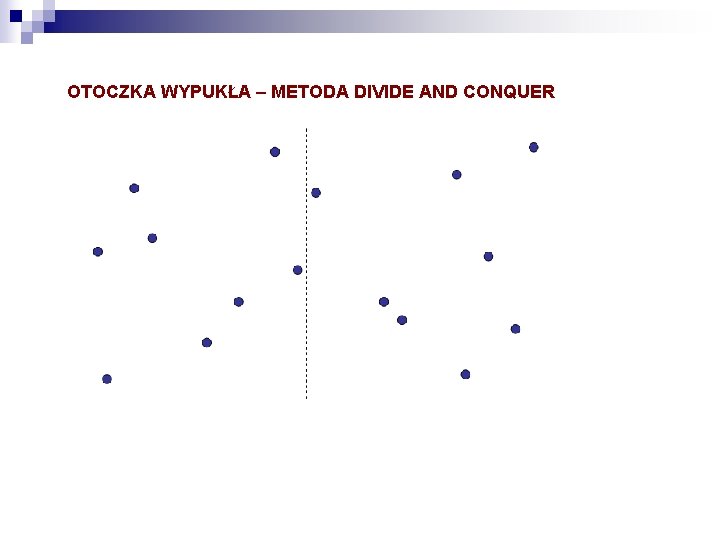
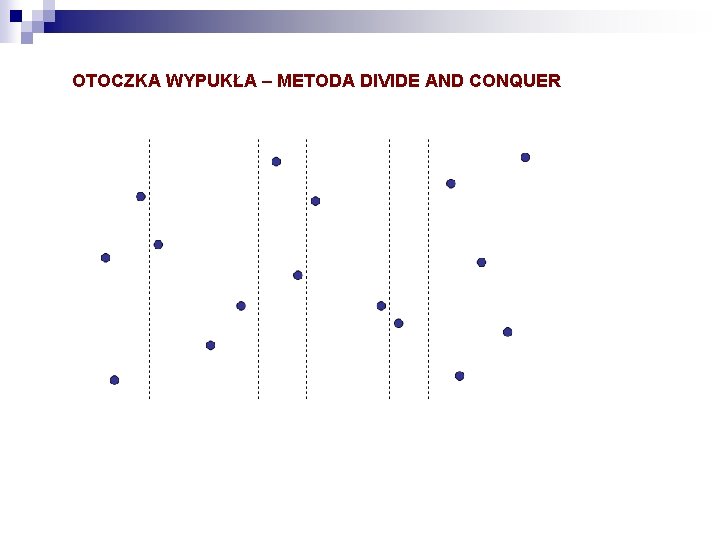
OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

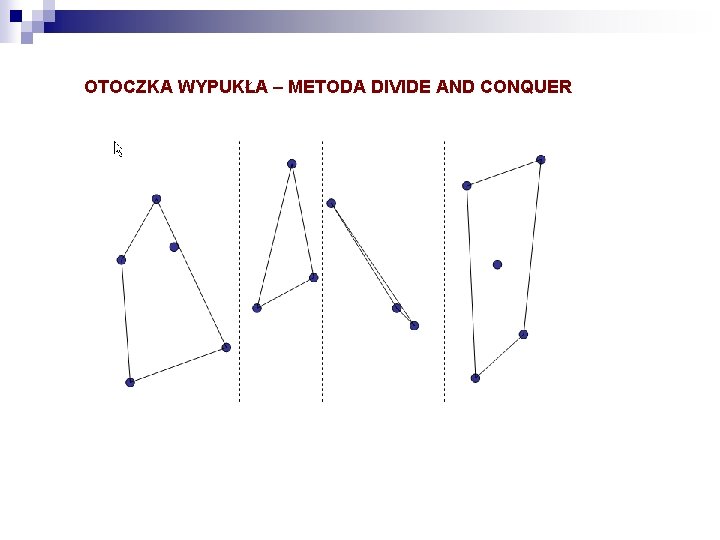
OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

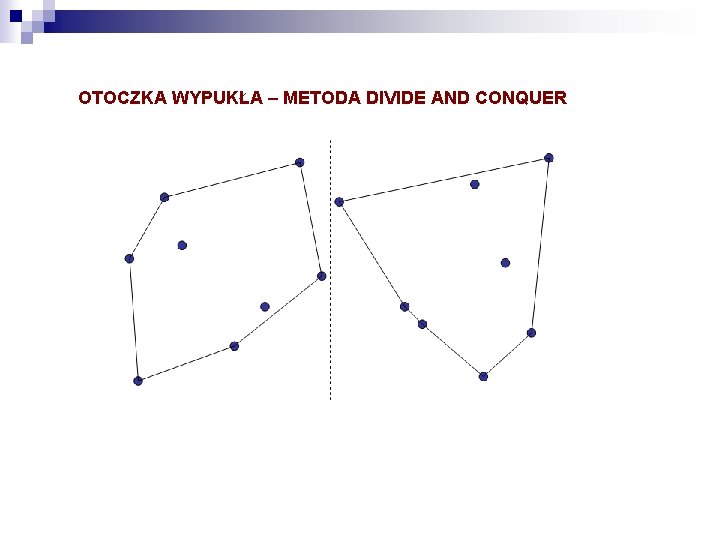
OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

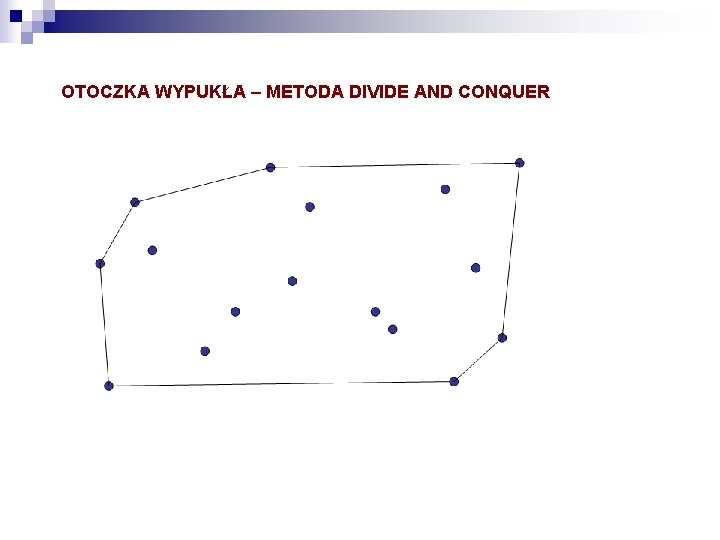
OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

OTOCZKA WYPUKŁA – METODA DIVIDE AND CONQUER

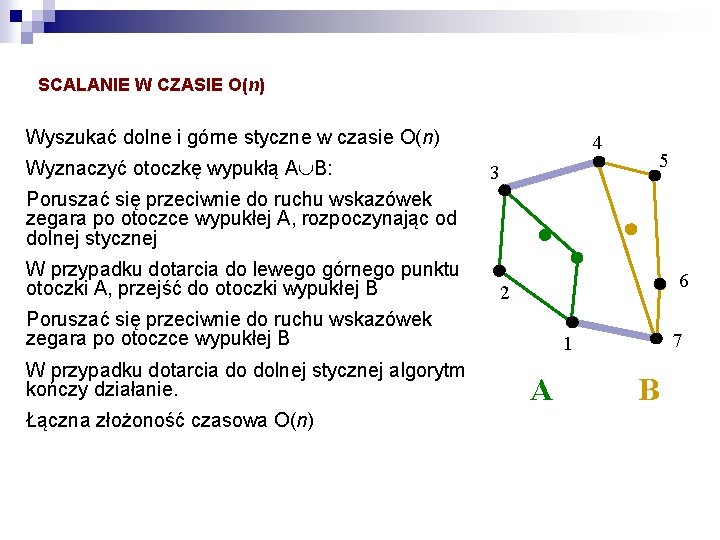
SCALANIE W CZASIE O(n) Wyszukać dolne i górne styczne w czasie O(n) Wyznaczyć otoczkę wypukłą A B: 4 3 5 Poruszać się przeciwnie do ruchu wskazówek zegara po otoczce wypukłej A, rozpoczynając od dolnej stycznej W przypadku dotarcia do lewego górnego punktu otoczki A, przejść do otoczki wypukłej B 6 2 Poruszać się przeciwnie do ruchu wskazówek zegara po otoczce wypukłej B W przypadku dotarcia do dolnej stycznej algorytm kończy działanie. Łączna złożoność czasowa O(n) 7 1 A B

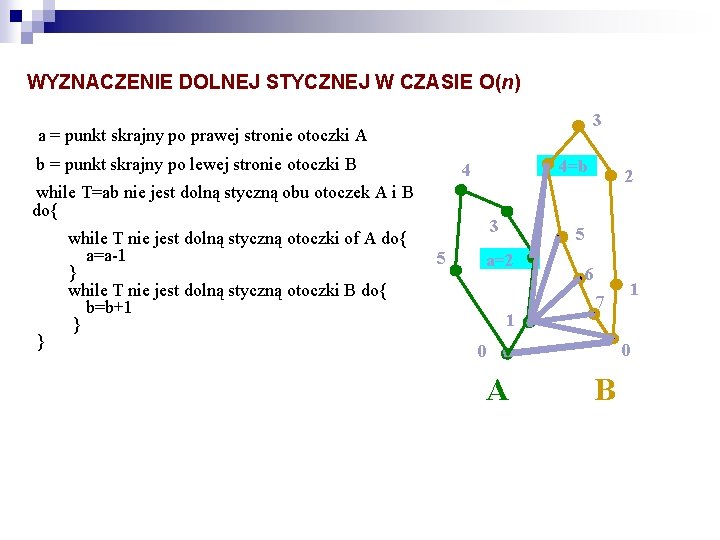
WYZNACZENIE DOLNEJ STYCZNEJ W CZASIE O(n) 3 a = punkt skrajny po prawej stronie otoczki A b = punkt skrajny po lewej stronie otoczki B 4=b 4 while T=ab nie jest dolną styczną obu otoczek A i B do{ } while T nie jest dolną styczną otoczki of A do{ a=a-1 } while T nie jest dolną styczną otoczki B do{ b=b+1 } 3 5 2 5 a=2 1 6 7 0 0 A 1 B

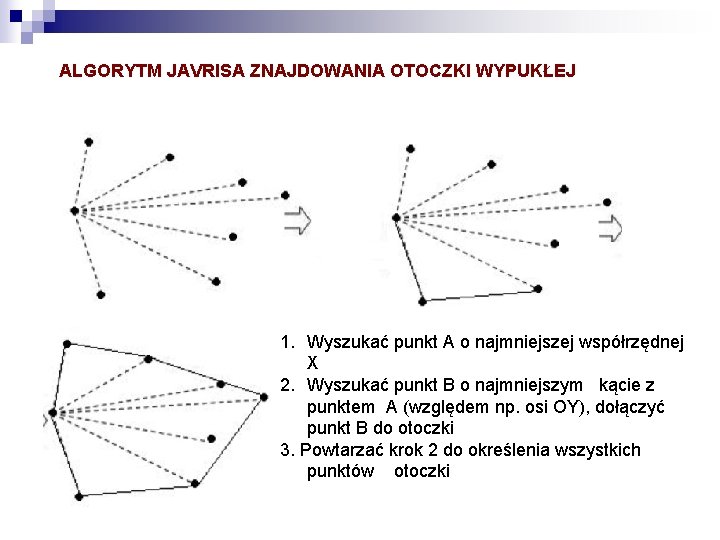
ALGORYTM JAVRISA ZNAJDOWANIA OTOCZKI WYPUKŁEJ 1. Wyszukać punkt A o najmniejszej współrzędnej X 2. Wyszukać punkt B o najmniejszym kącie z punktem A (względem np. osi OY), dołączyć punkt B do otoczki 3. Powtarzać krok 2 do określenia wszystkich punktów otoczki

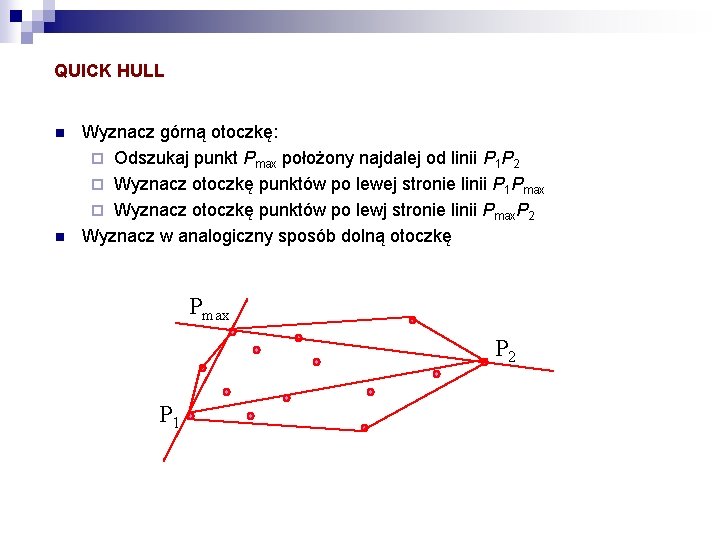
QUICK HULL n n Wyznacz górną otoczkę: ¨ Odszukaj punkt Pmax położony najdalej od linii P 1 P 2 ¨ Wyznacz otoczkę punktów po lewej stronie linii P 1 Pmax ¨ Wyznacz otoczkę punktów po lewj stronie linii Pmax. P 2 Wyznacz w analogiczny sposób dolną otoczkę Pmax P 2 P 1

METODY PDE W OPROGRAMOWANIU GIS n n n n n Image Enhancement Segmentation – segmentacja obrazu Edge Detection – wykrywanie krawędzi Shape-from-Shading Object Recognition – rozpoznawanie obiektów Shape Theory – algorytmy i teoria kształtu Optical Flow Visual Tracking Registration – rejestracja obrazu

RÓWNANIA LAGRANGE’A EULERA

RÓWNANIA LAGRANGE’A EULERA

RÓWNANIA LAGRANGE’A EULERA

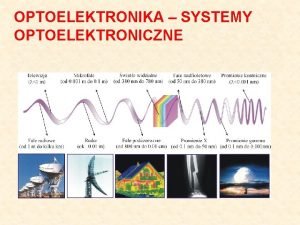
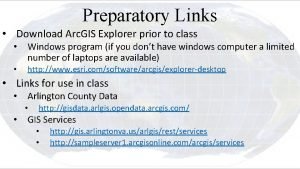
KRZYWE W PRZESTRZENI C(p)={x(p), y(p)}, p = [0, 1] C(0. 1) C(0. 2) C(0. 7) C(0) y C(0. 4) C(0. 95) C(0. 8) C(0. 9) x Cp =styczna

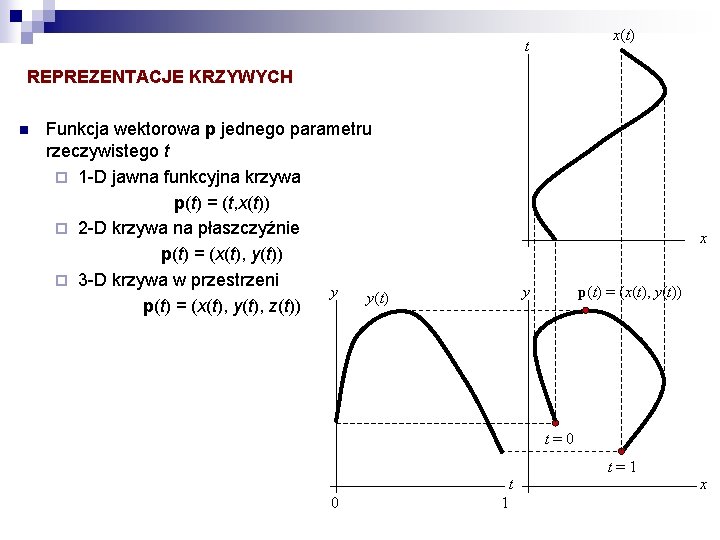
x(t) t REPREZENTACJE KRZYWYCH n Funkcja wektorowa p jednego parametru rzeczywistego t ¨ 1 -D jawna funkcyjna krzywa p(t) = (t, x(t)) ¨ 2 -D krzywa na płaszczyźnie p(t) = (x(t), y(t)) ¨ 3 -D krzywa w przestrzeni y y(t) p(t) = (x(t), y(t), z(t)) x y p(t) = (x(t), y(t)) t=0 t 0 1 t=1 x

WEKTOR STYCZNY n n n Pierwsza pochodna p’(t) wskazuje kierunek styczności p’(t) = (x’(t), y’(t), z’(t)) ¨ Kierunek stycznej T(t) = p’(t)/||p’(t)|| ¨ Szybkość parametryczna: ||p’(t)|| Wersja numeryczna (forward difference) p’(t) (p(t + t) – p(t))/ t ¨ Przydatna przy modelu gdy znamy jedynie wartości p(t) Wykorzystywana do określenia kierunku i szybkości p(t) p’(t) t=0 t=1

p(t) DŁUGOŚĆ ŁUKOWA p’(t) Parametryzacja długością łuku t=0 t=1 p(s) p’(s) n n Parameter s definiowany jako parameter t przy długości krzywej od p(0) to p(t) rónej s p(s) = {p(t) : s(t) = s} Stała szybkość: ||p’(s)|| = 1 s = s(0) = 0 s = s(1) = curve length

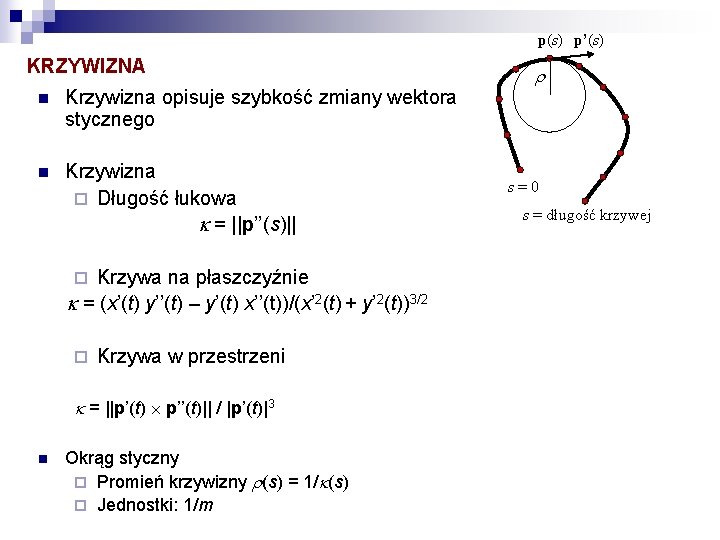
p(s) p’(s) KRZYWIZNA n Krzywizna opisuje szybkość zmiany wektora stycznego n Krzywizna ¨ Długość łukowa k = ||p’’(s)|| Krzywa na płaszczyźnie k = (x’(t) y’’(t) – y’(t) x’’(t))/(x’ 2(t) + y’ 2(t))3/2 ¨ ¨ Krzywa w przestrzeni k = ||p’(t) p’’(t)|| / |p’(t)|3 n Okrąg styczny ¨ Promień krzywizny r(s) = 1/k(s) ¨ Jednostki: 1/m r s=0 s = długość krzywej

ACTIVE CONTOURS Minimalizujemy funkcjonał: (patrz: równanie Lagrange’a Eulera) Pierwszy człon – elastyczność krzywej – pierwsza pochodna po funkcji krzywej w postaci parametrycznej łukowej Drugi człon – druga pochodna krzywej w postaci parametrycznej łukowej – krzywizna

ROZWIĄZANIE RÓWNANIA LAGRANGE’A EULERA Równanie rozwiązuje się metodą Eulera

LITERATURA 1. WYKŁAD, UKŁADY GEODEZYJNE I KARTOGRAFICZNE, J. BOSY, KGi. F 2. CHARAKTERYSTYKA UKŁADÓW WSPÓŁRZĘDNYCH STOSOWANYCH DO OPRACOWANIA MAP TOPOGRAFICZNYCH W POLSCE, R. Dorożyński 3. JERZY B. ROGOWSKI, M. FIGURSKI, Instytut Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej ZIEMSKIE SYSTEMY I UKŁADY ODNIESIENIA ORAZ ICH REALIZACJE 4. ODWZOROWANIA KARTOGRAFICZNE, H. KLIMCZAK, WYKŁADY