ELEG 479 Lecture 8 Mark Mirotznik Ph D

ELEG 479 Lecture #8 Mark Mirotznik, Ph. D. Associate Professor The University of Delaware

Summary of Last Lecture X-ray Radiography q Overview of different systems for projection radiography q Instrumentation q Overall system layout q X-ray sources q grids and filters q detectors q Imaging Equations q Basic equations q Geometrical distortions q More complicated imaging equations

Hounsfield’s Experimental CT

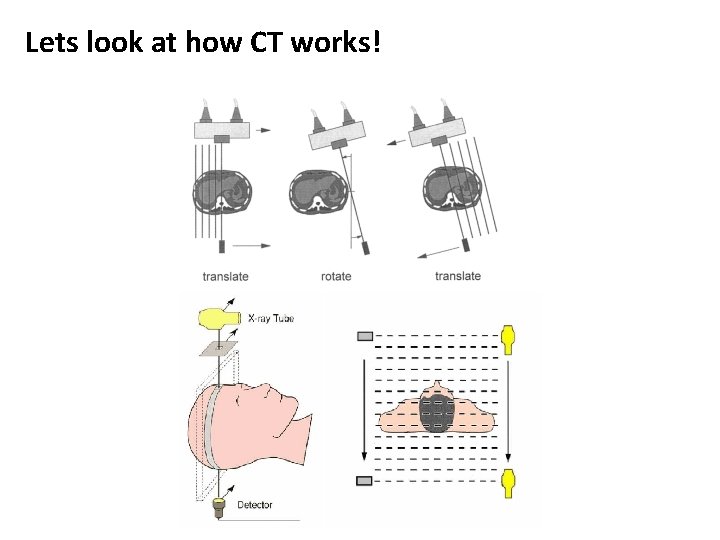
Lets look at how CT works!

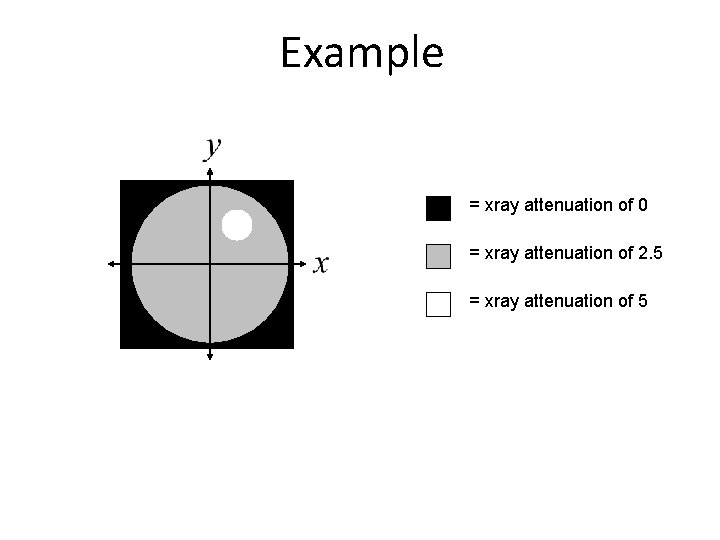
Example = xray attenuation of 0 = xray attenuation of 2. 5 = xray attenuation of 5

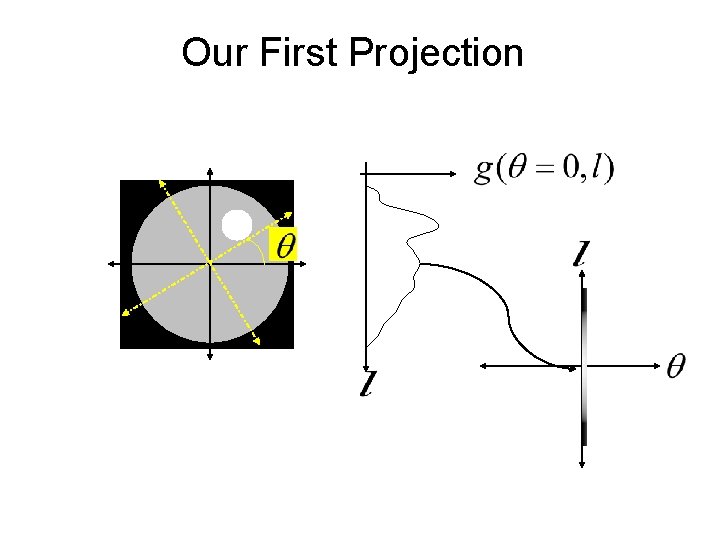
Our First Projection

Our First Projection

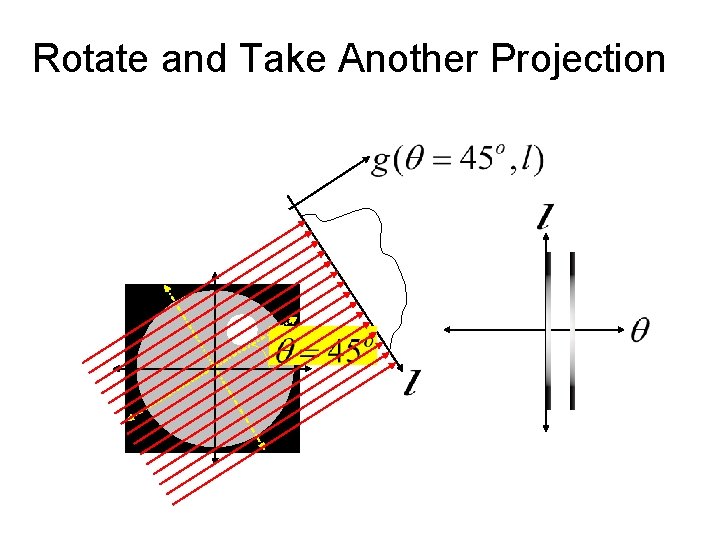
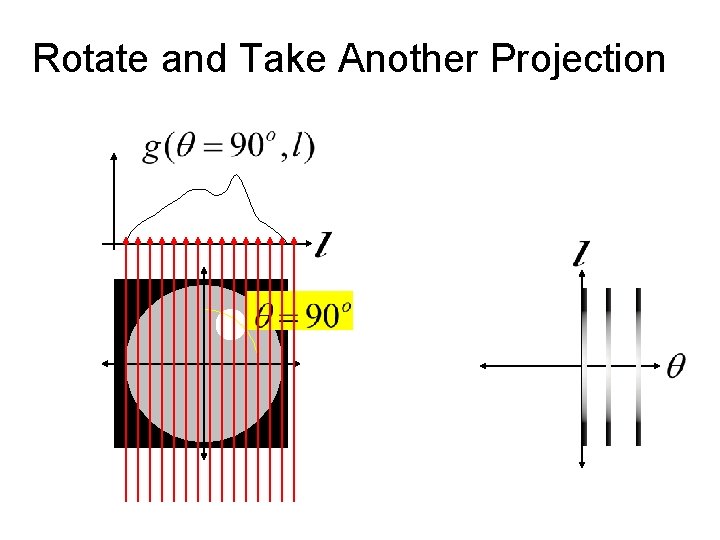
Rotate and Take Another Projection

Rotate and Take Another Projection

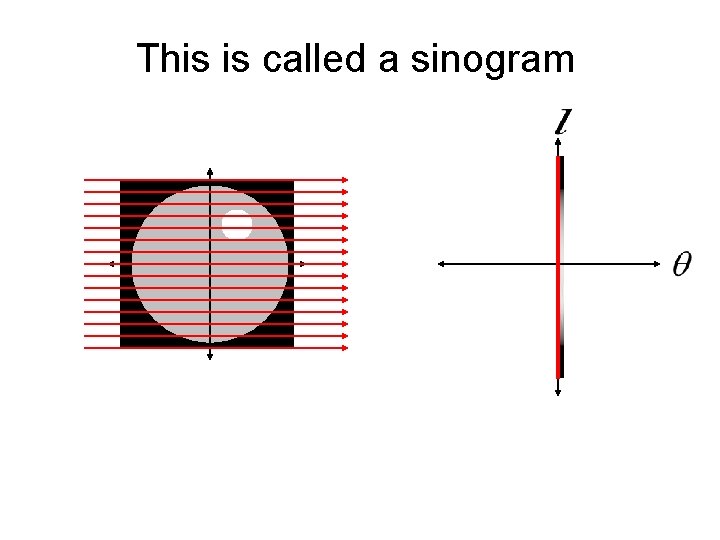
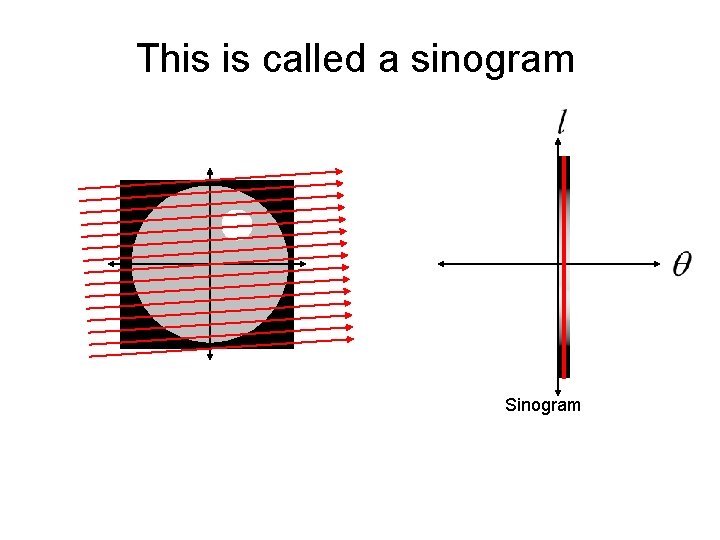
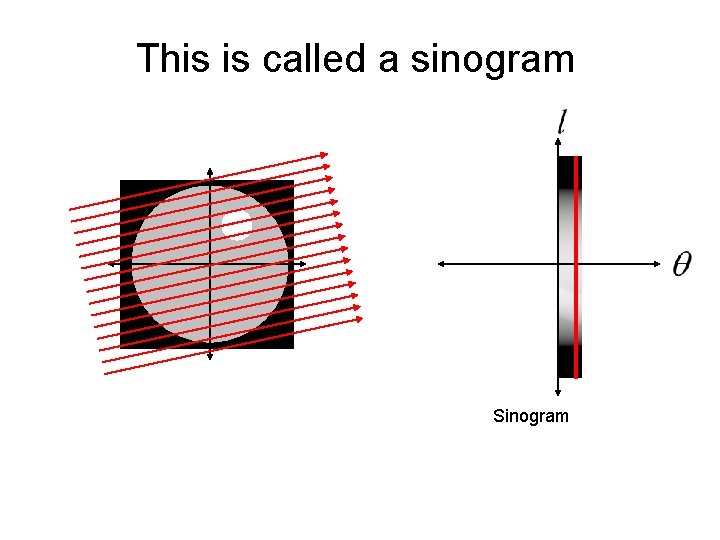
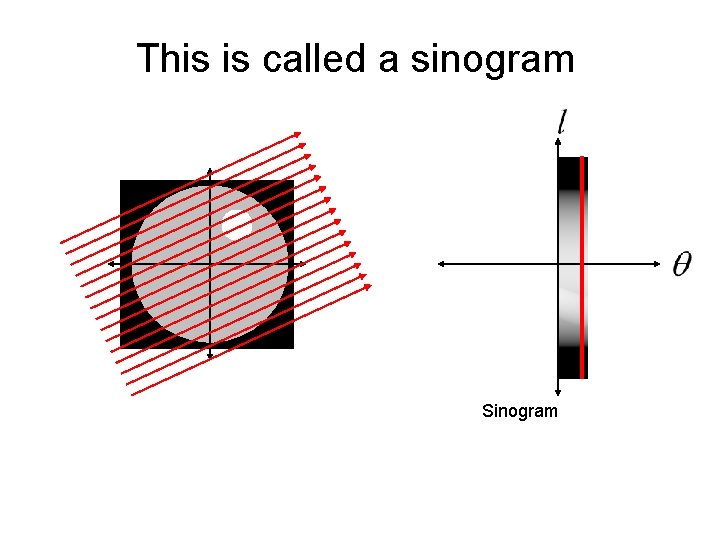
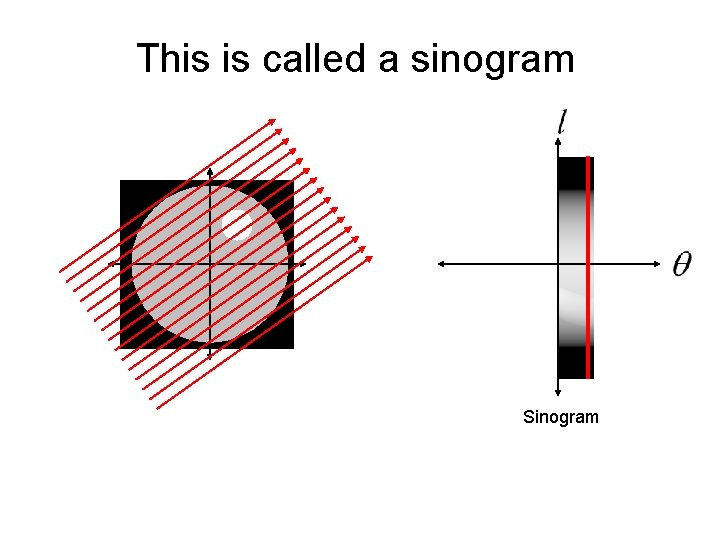
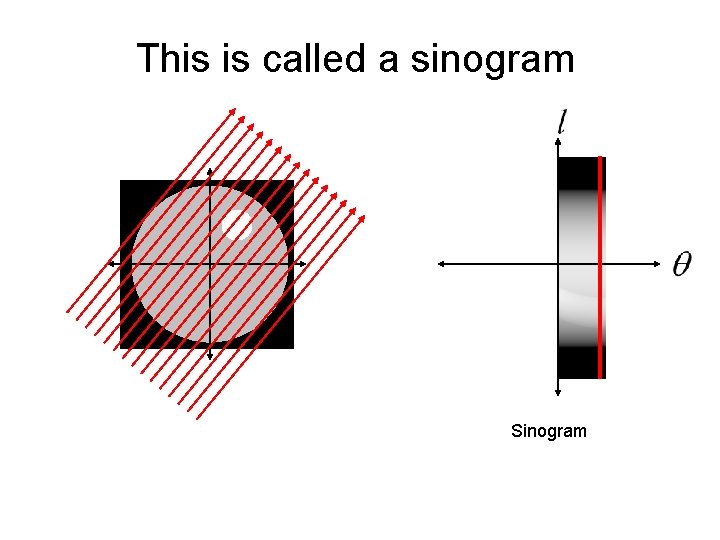
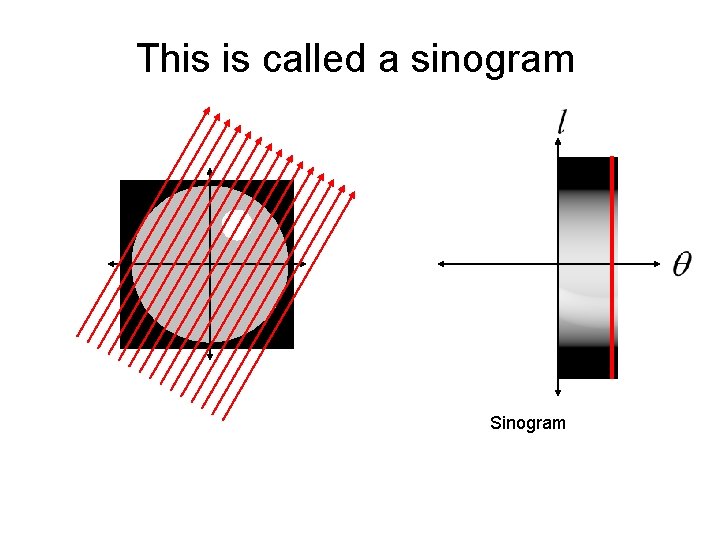
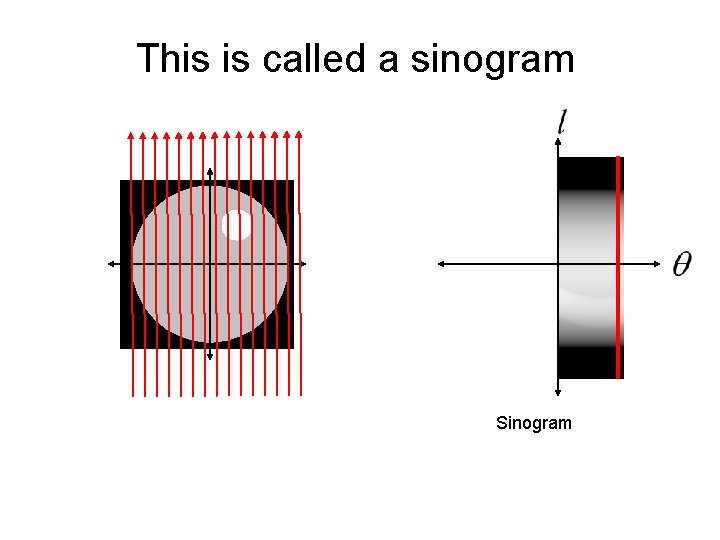
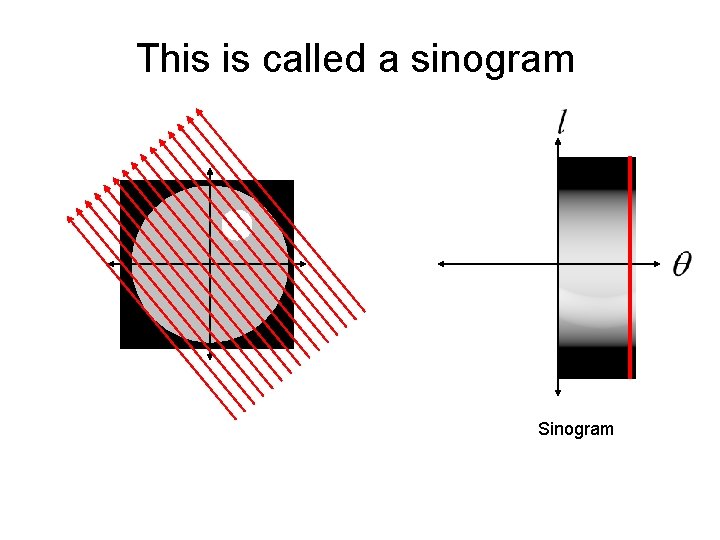
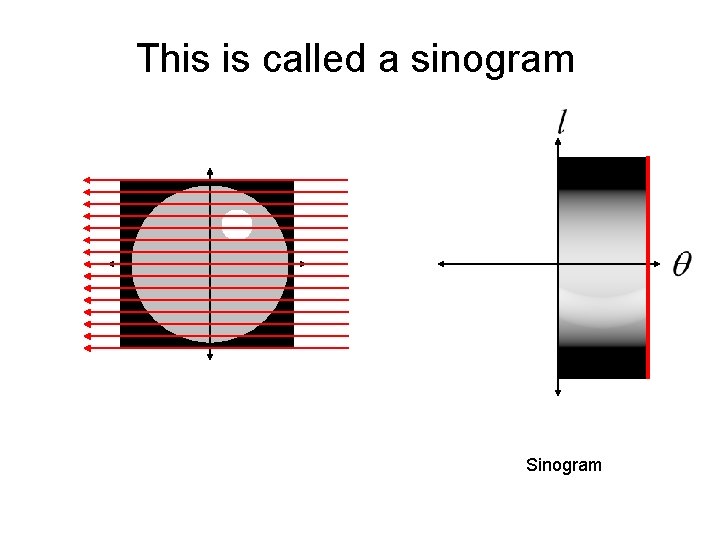
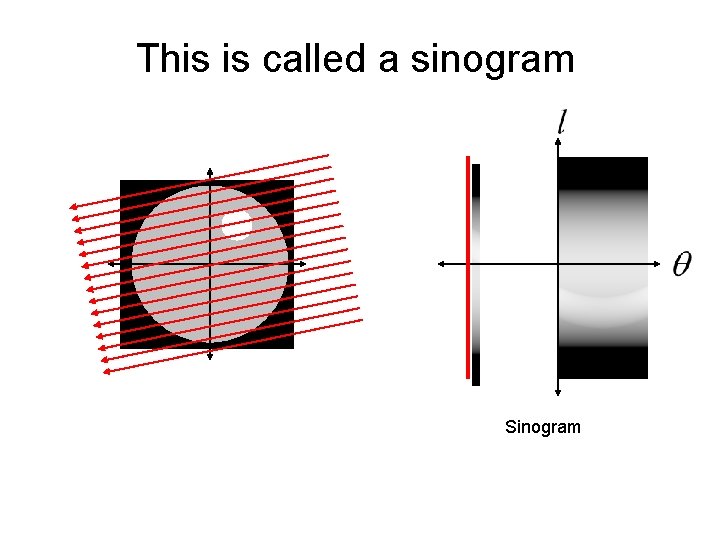
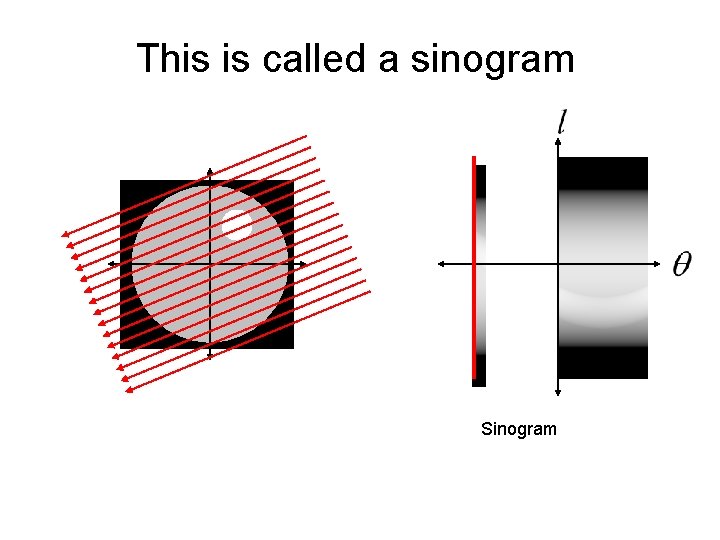
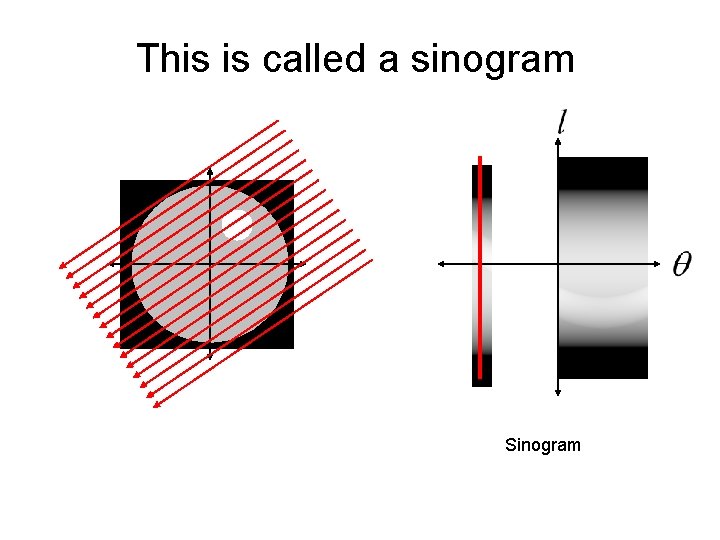
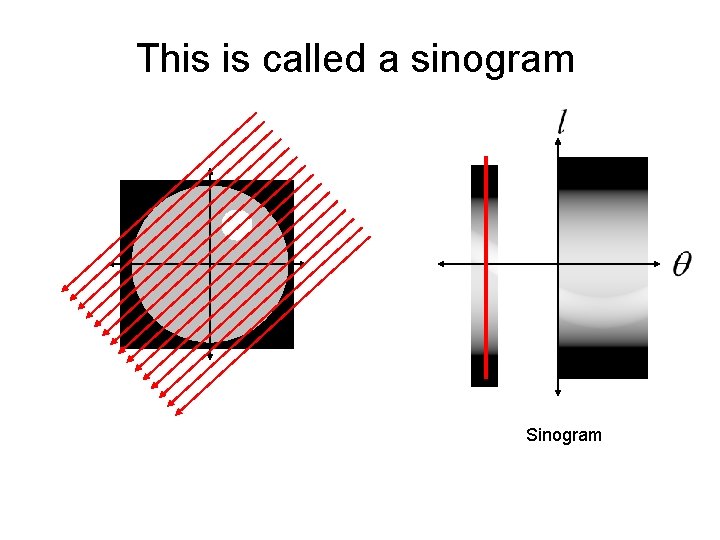
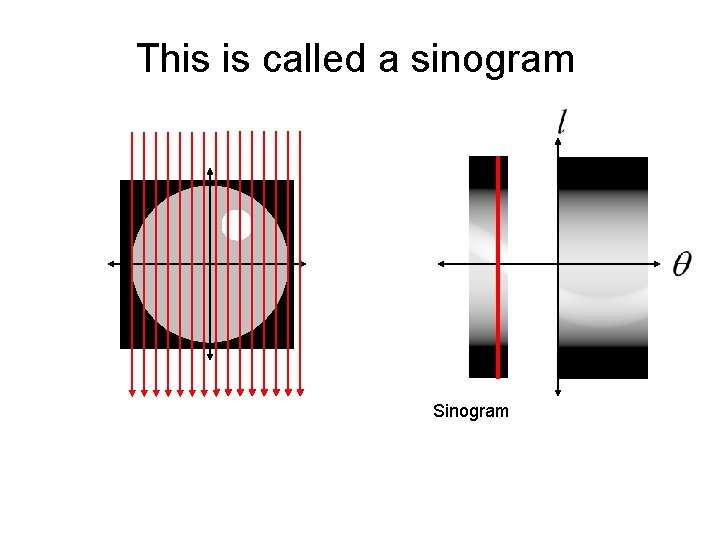
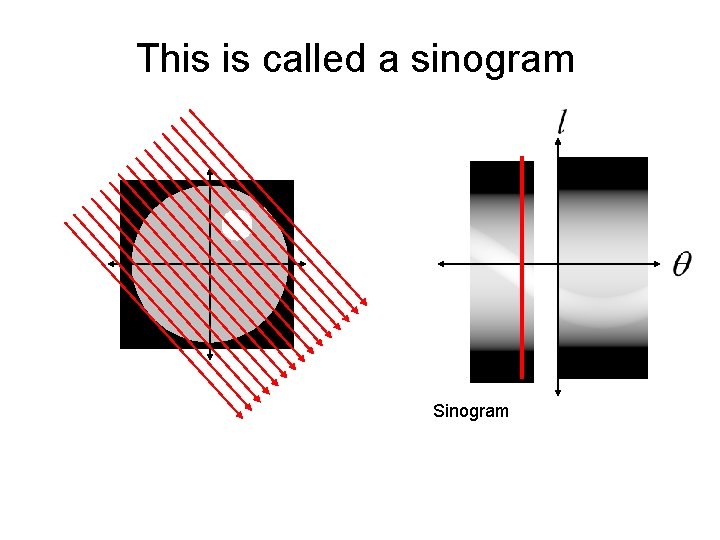
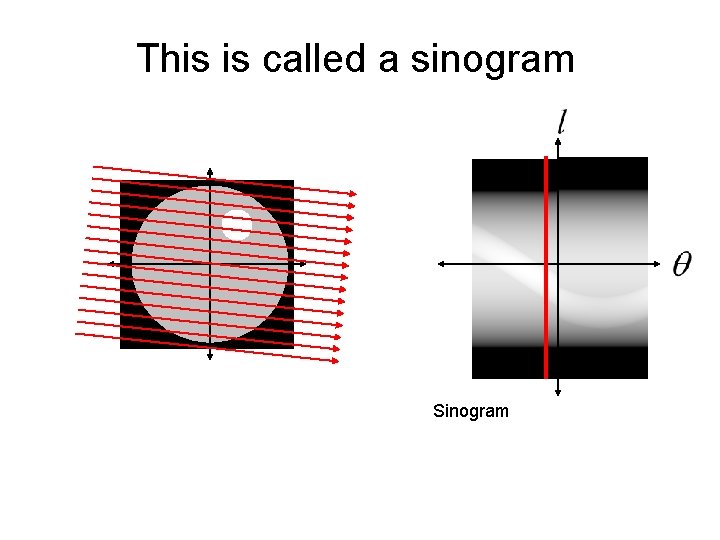
This is called a sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

This is called a sinogram Sinogram

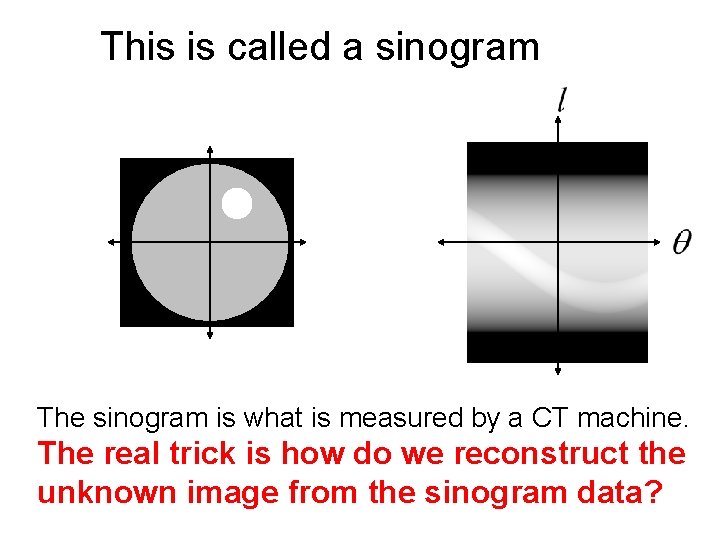
This is called a sinogram The sinogram is what is measured by a CT machine. The real trick is how do we reconstruct the unknown image from the sinogram data?

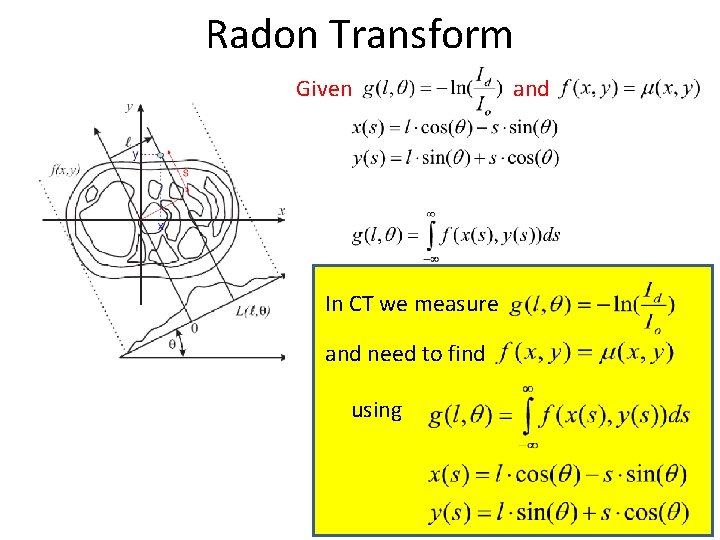
Radon Transform Given In CT we measure and need to find using and

Radon Transform In CT we measure and need to find We use

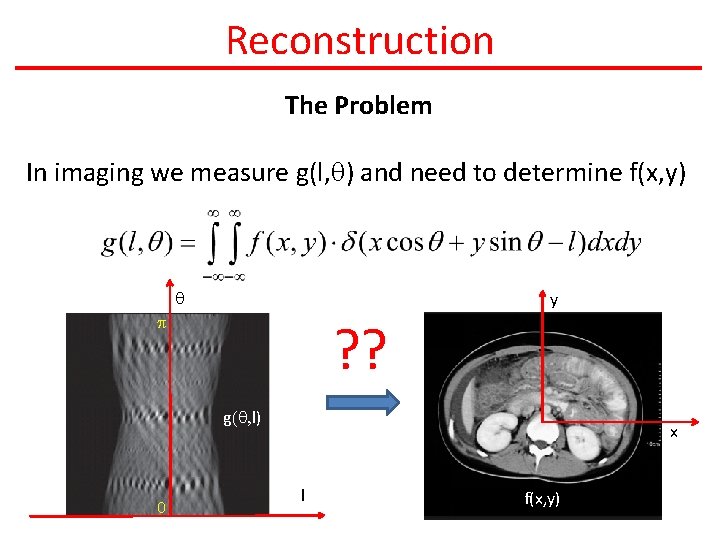
Reconstruction The Problem In imaging we measure g(l, q) and need to determine f(x, y) q y p ? ? g(q, l) 0 x l f(x, y)

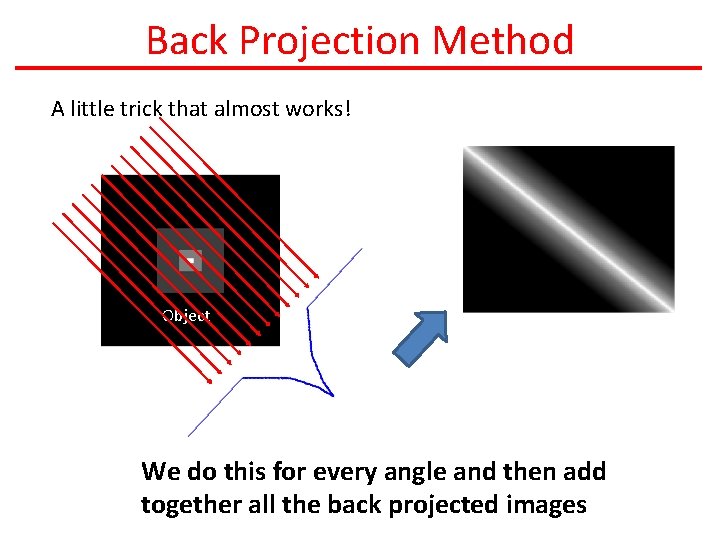
Back Projection Method A little trick that almost works! Object

Back Projection Method A little trick that almost works! Object We do this for every angle and then add together all the back projected images

Back Projection Method Step #1: Generate a complete an image for each projection (e. g. for each angle q) These are called back projected images Step #2: Add all the back projected images together

Back Projection Method Original object Reconstructed object Kind of worked but we need to do better than this. Need to come up with a better reconstruction algorithm.

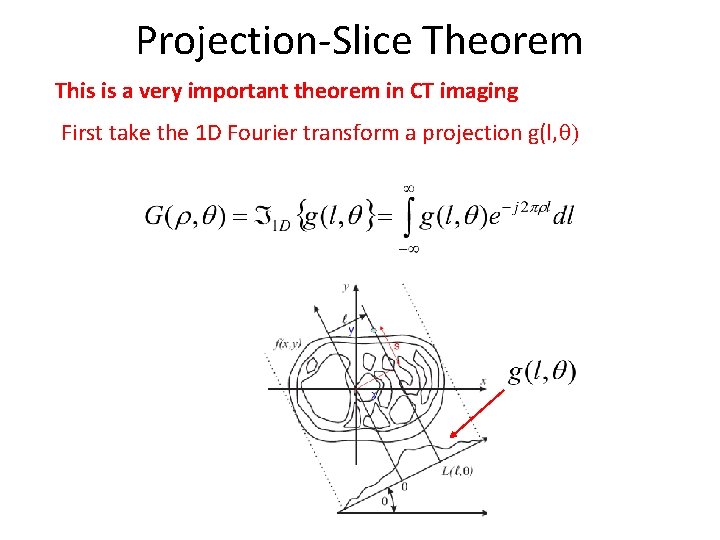
Projection-Slice Theorem This is a very important theorem in CT imaging First take the 1 D Fourier transform a projection g(l, q)

Projection-Slice Theorem This is a very important theorem in CT imaging First take the 1 D Fourier transform a projection g(l, q) Next we substitute the Radon transform for g(l, q)

Projection-Slice Theorem This is a very important theorem in CT imaging First take the 1 D Fourier transform a projection g(l, q) Next we substitute the Radon transform for g(l, q) Next we do a little rearranging

Projection-Slice Theorem This is a very important theorem in CT imaging Next we do a little rearranging Applying the properties of the delta function What does this look like?

Projection-Slice Theorem This is a very important theorem in CT imaging What does this look like? This looks a lot like with

Projection-Slice Theorem This is a very important theorem in CT imaging So what does this mean?

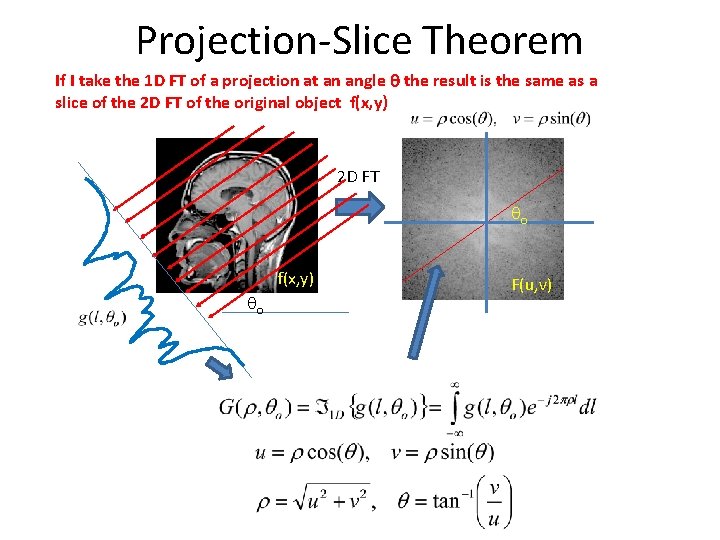
Projection-Slice Theorem This is a very important theorem in CT imaging Question: So what does this mean? Answer: If I take the 1 D FT of a projection at an angle q the result is the same as a slice of the 2 D FT of the original object f(x, y)

Projection-Slice Theorem This is a very important theorem in CT imaging So what does this mean? If I take the 1 D FT of a projection at an angle q the result is the same as a slice of the 2 D FT of the original object f(x, y)

Projection-Slice Theorem If I take the 1 D FT of a projection at an angle q the result is the same as a slice of the 2 D FT of the original object f(x, y) 2 D FT qo f(x, y) qo F(u, v)

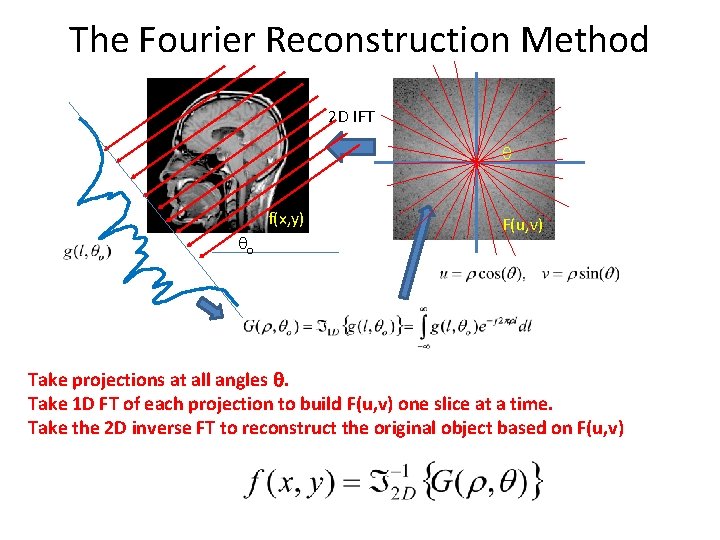
The Fourier Reconstruction Method 2 D IFT q f(x, y) qo F(u, v) Take projections at all angles q. Take 1 D FT of each projection to build F(u, v) one slice at a time. Take the 2 D inverse FT to reconstruct the original object based on F(u, v)

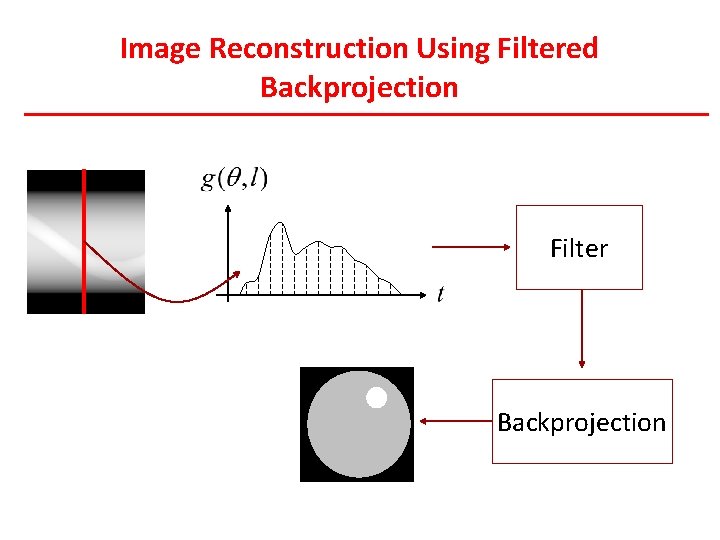
Image Reconstruction Using Filtered Backprojection Filter Backprojection

Filtered Back Projection The Fourier method is not widely used in CT because of the computational issues with creating the 2 D FT from projections. However, the method does lead to a popular technique called filtered back projection. In polar coordinates the inverse Fourier transform can be written as with

Filtered Back Projection The Fourier method is not widely used in CT because of the computational issues with creating the 2 D FT from projections. However, the method does lead to a popular technique called filtered back projection. In polar coordinates the inverse Fourier transform can be written as with From the projection theorem We can write this as

Filtered Back Projection The Fourier method is not widely used in CT because of the computational issues with creating the 2 D FT from projections. However, the method does lead to a popular technique called filtered back projection. We can write this as Since which can be rewritten as you can show

Filtered Back Projection verses Back Projection A. Back Projection B. Filtered Back Projection

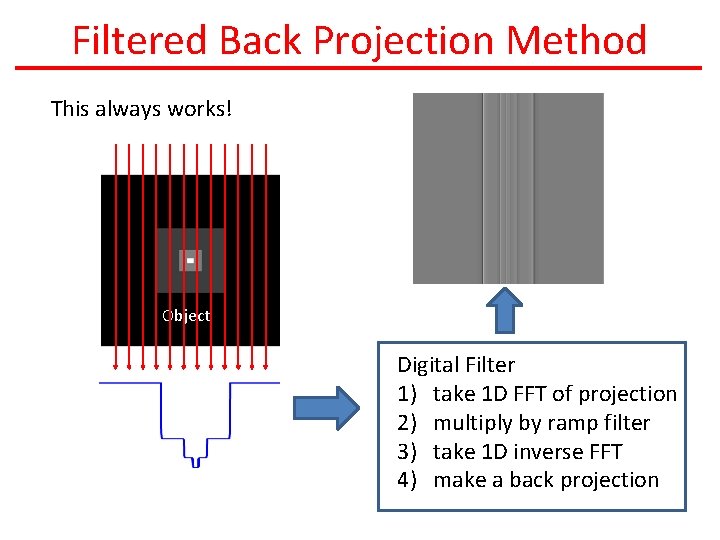
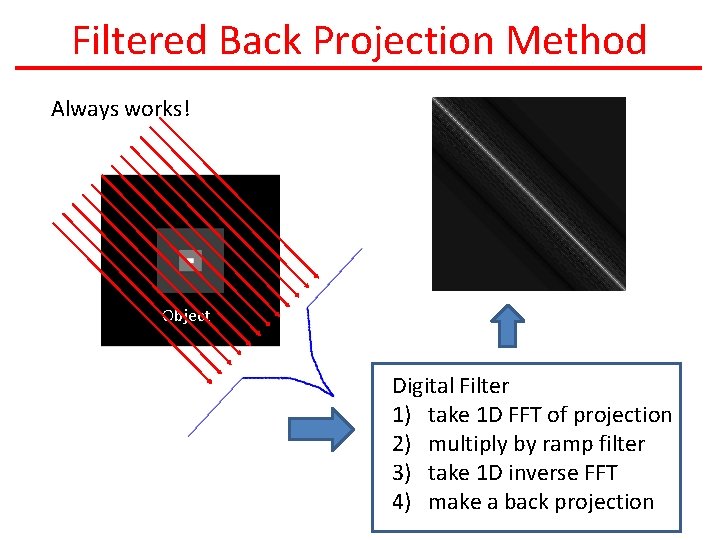
Filtered Back Projection Method This always works! Object Digital Filter 1) take 1 D FFT of projection 2) multiply by ramp filter 3) take 1 D inverse FFT 4) make a back projection

Filtered Back Projection Method Always works! Object Digital Filter 1) take 1 D FFT of projection 2) multiply by ramp filter 3) take 1 D inverse FFT 4) make a back projection

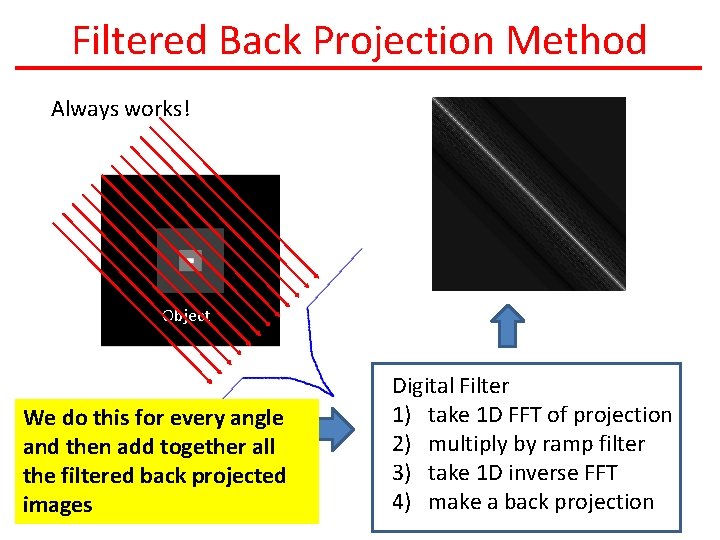
Filtered Back Projection Method Always works! Object We do this for every angle and then add together all the filtered back projected images Digital Filter 1) take 1 D FFT of projection 2) multiply by ramp filter 3) take 1 D inverse FFT 4) make a back projection

Filtered Back Projection verses Back Projection A. Back Projection Matlab Demo Your Assignment (b) Write a matlab function that reconstructs an image using the filtered back projection method B. Filtered Back Projection

Convolution Back Projection From the filtered back projection algorithm we get It may be easier computationally to compute the inner 1 D IFT using a convolution recall

Convolution Back Projection Let

Convolution Back Projection The problem is does not exist

Convolution Back Projection The problem is does not exist The solution where is called a weighting function

Convolution Back Projection Common window functions § Hamming window § Lanczos window (sinc function) § Simple rectangular window § Ram-Lak window § Kaiser window § Shepp-Logan window

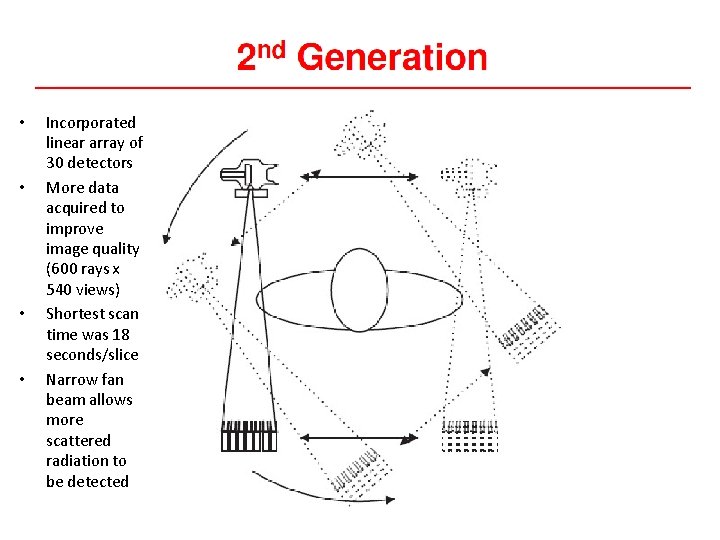
• • Incorporated linear array of 30 detectors More data acquired to improve image quality (600 rays x 540 views) Shortest scan time was 18 seconds/slice Narrow fan beam allows more scattered radiation to be detected

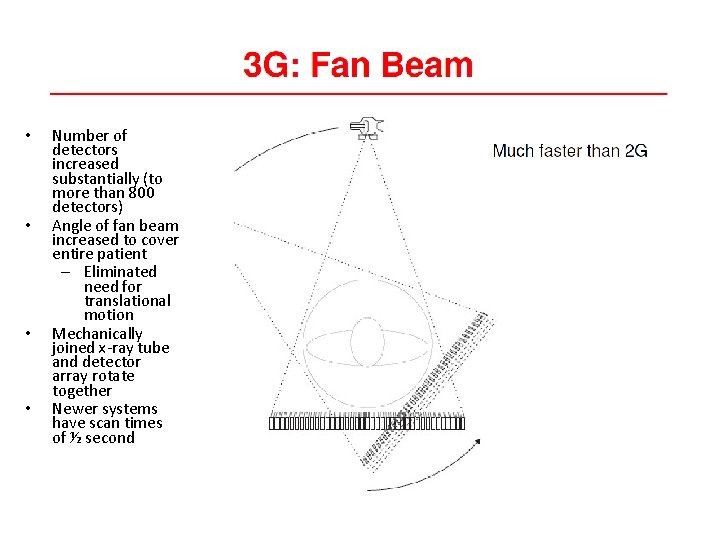
• • Number of detectors increased substantially (to more than 800 detectors) Angle of fan beam increased to cover entire patient – Eliminated need for translational motion Mechanically joined x-ray tube and detector array rotate together Newer systems have scan times of ½ second

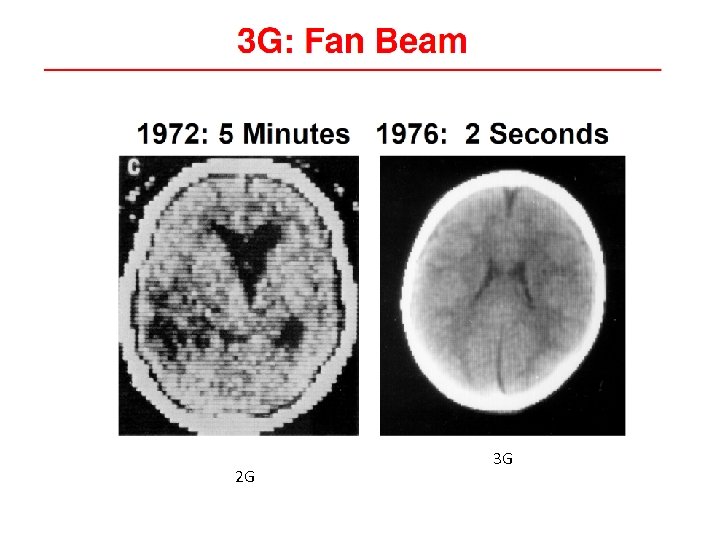
2 G 3 G

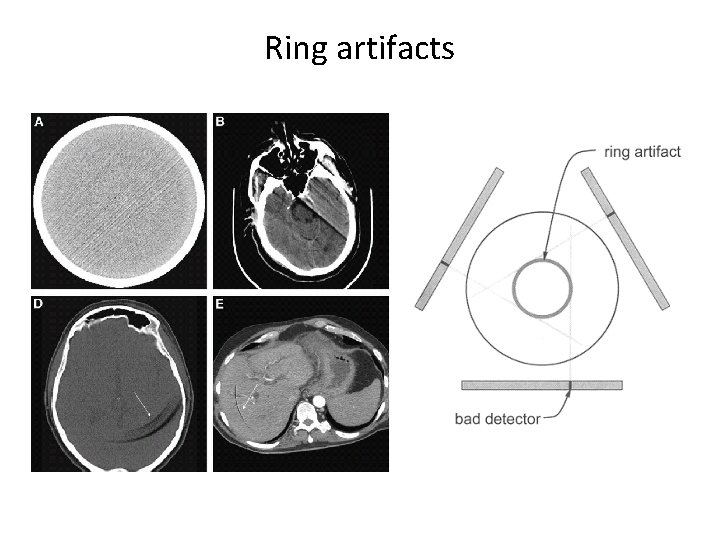
Ring artifacts • The rotate/rotate geometry of 3 rd generation scanners leads to a situation in which each detector is responsible for the data corresponding to a ring in the image • Drift in the signal levels of the detectors over time affects the t values that are backprojected to produce the CT image, causing ring artifacts

Ring artifacts

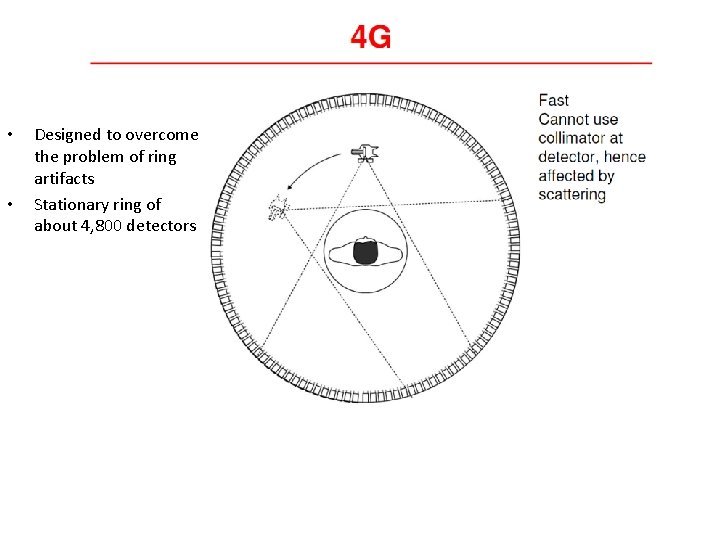
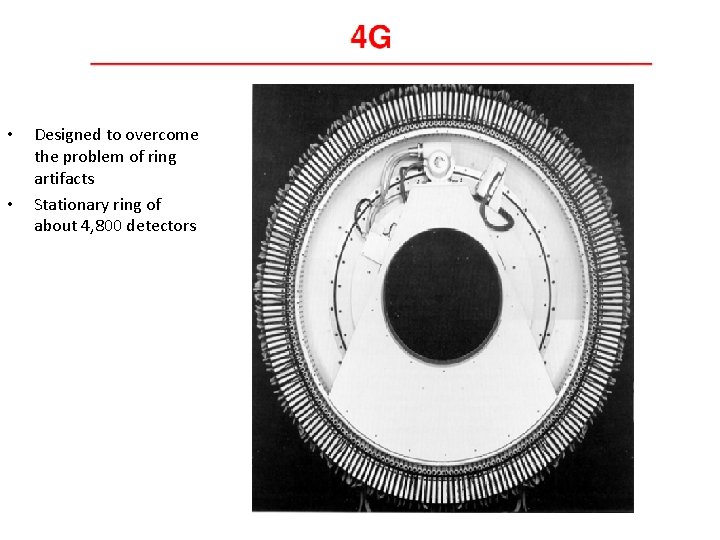
• • Designed to overcome the problem of ring artifacts Stationary ring of about 4, 800 detectors

• • Designed to overcome the problem of ring artifacts Stationary ring of about 4, 800 detectors

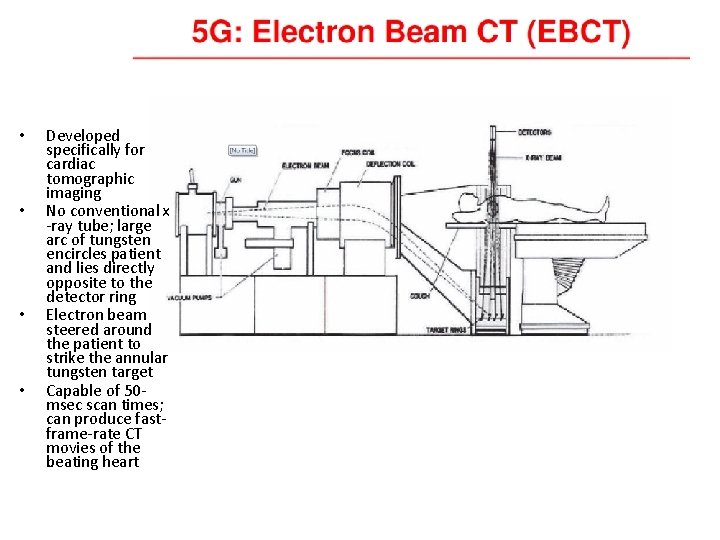
• • Developed specifically for cardiac tomographic imaging No conventional x -ray tube; large arc of tungsten encircles patient and lies directly opposite to the detector ring Electron beam steered around the patient to strike the annular tungsten target Capable of 50 msec scan times; can produce fastframe-rate CT movies of the beating heart

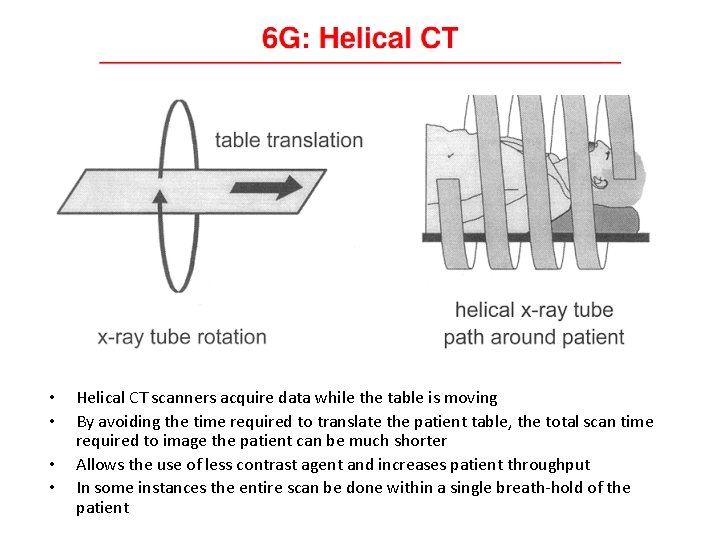
• • Helical CT scanners acquire data while the table is moving By avoiding the time required to translate the patient table, the total scan time required to image the patient can be much shorter Allows the use of less contrast agent and increases patient throughput In some instances the entire scan be done within a single breath-hold of the patient

Computer Assignment 1. Write a MATLAB program that reconstructs an image from its projections using the back projection method. Your program should allow the user to input a phantom object and a set (e. g. vector) of projection angle. Your program should then: (a) compute the sinogram of the object (you can use Matlab’s radon. m command to do this), (b) compute the reconstructed image from the sinogram and vector of projection angles, (c) try your program out for several different objects and several different ranges of projection angles 2. Do the same as #1 using the filter back projection method. 3. (grad students only) Do the same with the convolution back projection method