ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture

ECE 576 POWER SYSTEM DYNAMICS AND STABILITY Lecture 4 Synchronous Machine Dynamics Professor Pete Sauer Department of Electrical and Computer Engineering © 2000 University of Illinois Board of Trustees, All Rights Reserved

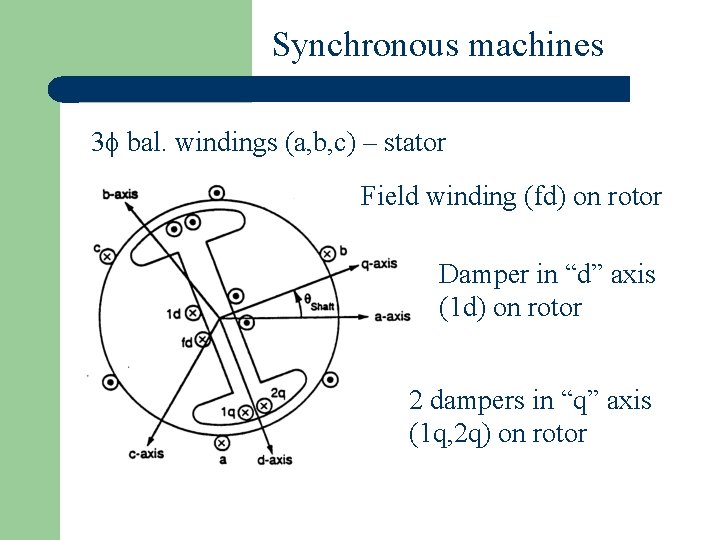
Synchronous machines 3 bal. windings (a, b, c) – stator Field winding (fd) on rotor Damper in “d” axis (1 d) on rotor 2 dampers in “q” axis (1 q, 2 q) on rotor

Fundamental laws Kirchhoff’s Voltage Law, Ohm’s Law, Faraday’s Law, Newton’s Second Law Stator Rotor Shaft

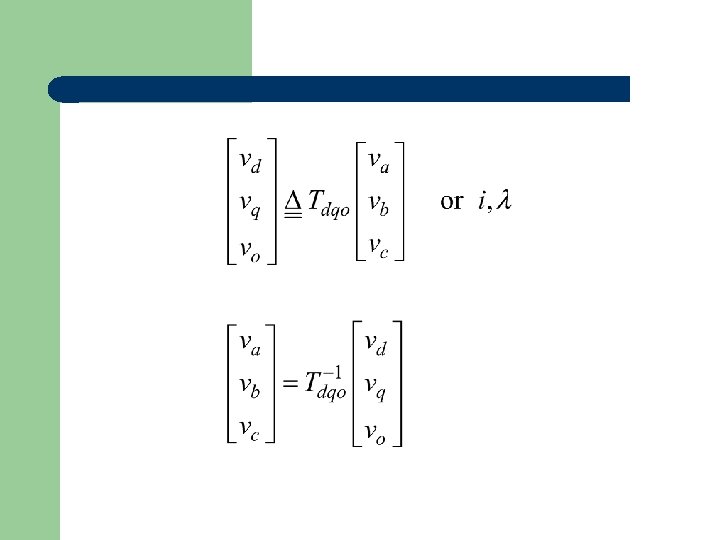
with the inverse,

Note: This transformation is not power invariant. This means that some unusual things will happen when we use it. Example: If the magnetic circuit is assumed to be linear (symmetric) Not symmetric if T is not power invariant.

Look at the instantaneous power:

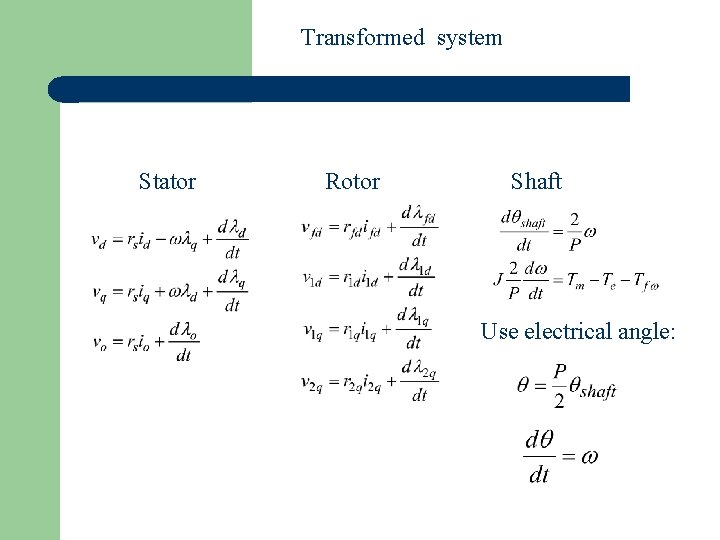
Transformed system Stator Rotor Shaft Use electrical angle:

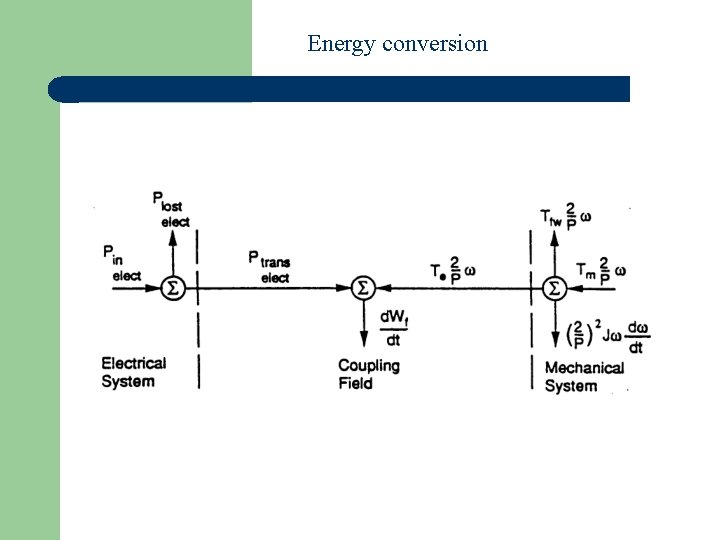
Energy conversion

Change to conservation of power Electrical system: Mechanical system:

Coupling field summation This assumes a lossless coupling field.

For independent states , a, b, c, fd, 1 q, 2 q

Equate coefficients etc. There are eight such “reciprocity conditions for this model. These are key conditions – i. e. the first one gives an expression for the torque in terms of the coupling field energy.

Look at this in the transformed variables

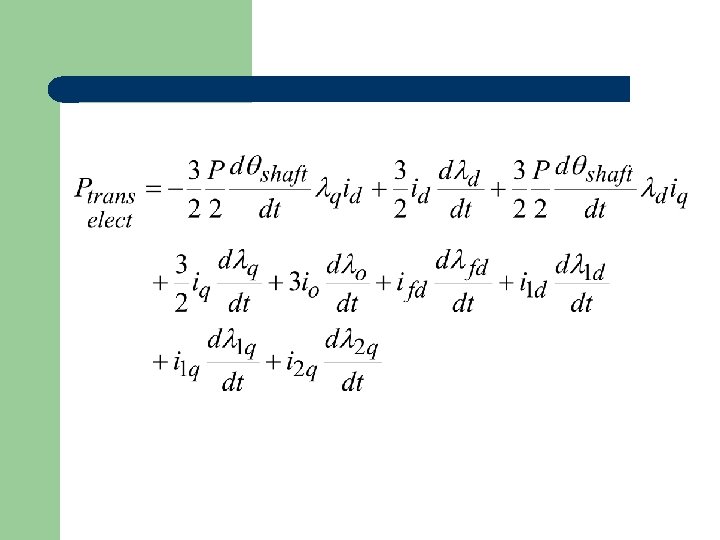
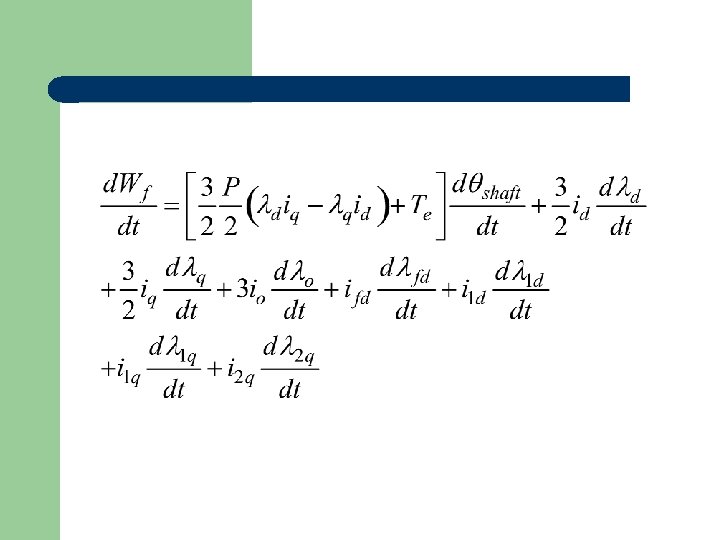
For independent states shaft, d, q, o, fd, 1 d, 1 q, 2 q

Equate coefficients

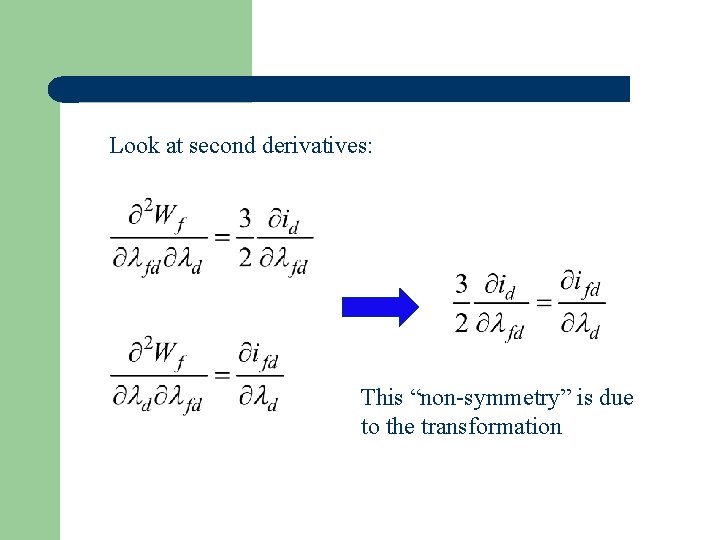
Look at second derivatives: This “non-symmetry” is due to the transformation

Will show that: So that: Which gives us an expression for torque in terms of flux linkage and current (for linear or nonlinear magnetic model).

Notice the important difference between “abc” variables and “qdo” variables:

Change of variables in integration

This is a path integral. Because the coupling field is lossless, it can be shown that the path of integration is arbitrary. Start with de-energized system so that:

Integrate theta first (while the electrical system is off). Wf stays at zero because the torque and all electrical variables are still zero. Assume: iq, id, io, ifd, i 1 q, i 2 q are independent of shaft (current/flux linkage relationship is independent of shaft). Then Wf will be independent of theta also!

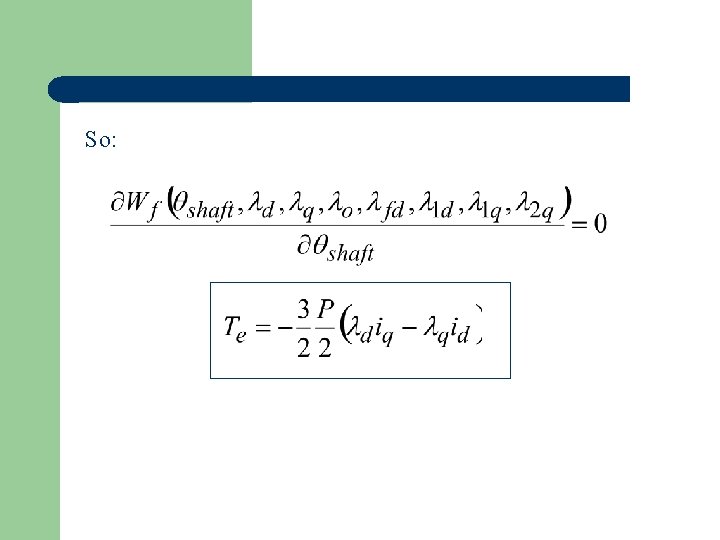
So: