Introduction to Neural Networks and Fuzzy Logic Lecture

Introduction to Neural Networks and Fuzzy Logic Lecture 8 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com President University Erwin Sitompul NNFL 8/1

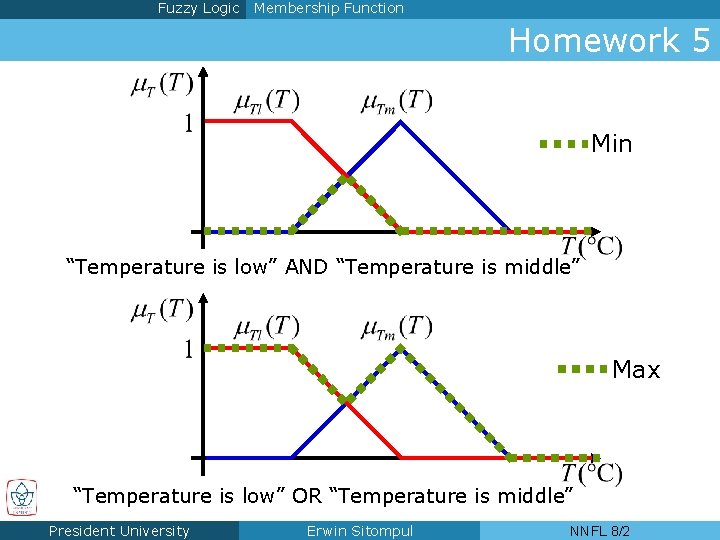
Fuzzy Logic Membership Function Homework 5 Min “Temperature is low” AND “Temperature is middle” Max “Temperature is low” OR “Temperature is middle” President University Erwin Sitompul NNFL 8/2

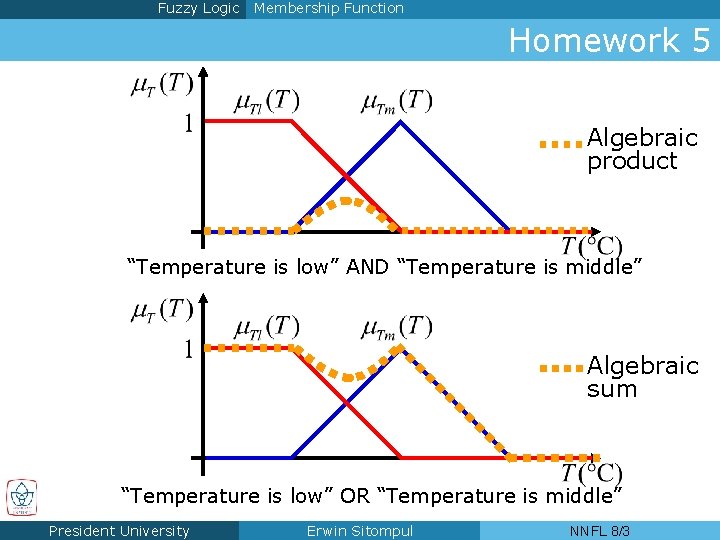
Fuzzy Logic Membership Function Homework 5 Algebraic product “Temperature is low” AND “Temperature is middle” Algebraic sum “Temperature is low” OR “Temperature is middle” President University Erwin Sitompul NNFL 8/3

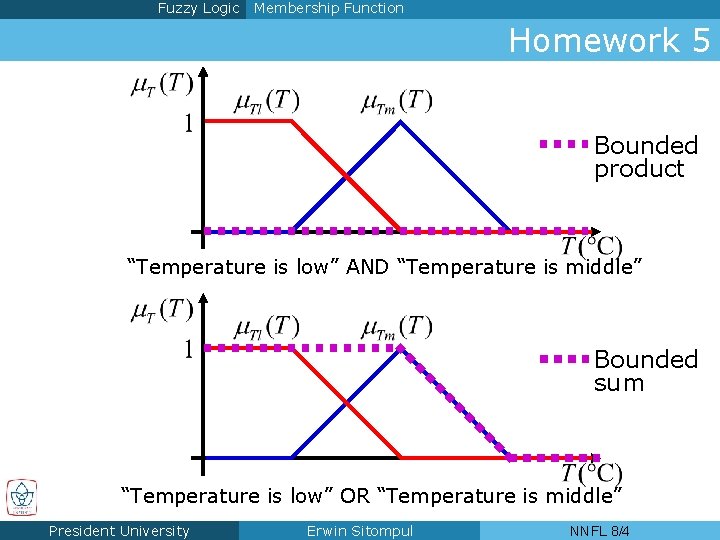
Fuzzy Logic Membership Function Homework 5 Bounded product “Temperature is low” AND “Temperature is middle” Bounded sum “Temperature is low” OR “Temperature is middle” President University Erwin Sitompul NNFL 8/4

Linguistic Variables and Term Set Term set : family of membership functions President University Erwin Sitompul NNFL 8/5

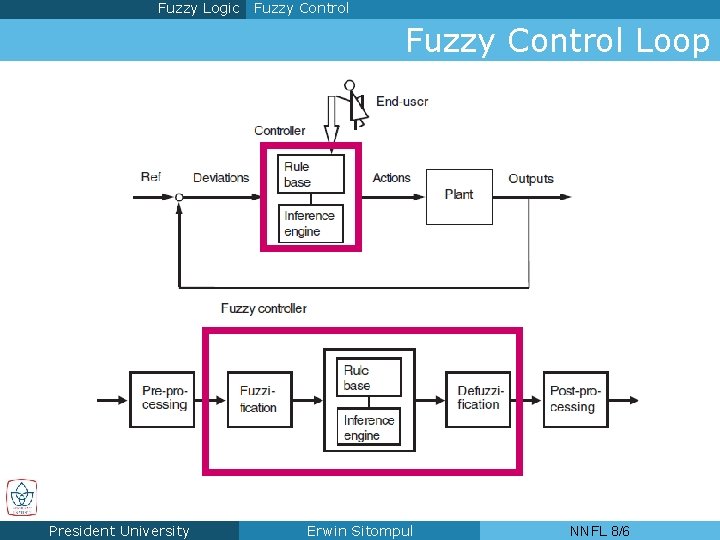
Fuzzy Logic Fuzzy Control Loop President University Erwin Sitompul NNFL 8/6

Fuzzy Logic Fuzzy Control Fuzzy Interference n Prior to fuzzy control, the followings must be defined: n Fuzzy membership functions n Fuzzy logical operators Min-Max, Algebraic, Bounded n Fuzzy rules IF-THEN rules n The processing steps in a fuzzy control include: n Fuzzification n Implication n Accumulation n Defuzzification President University Erwin Sitompul NNFL 9/7

Fuzzy Logic Fuzzy Control Fuzzy Rules n Example of a fuzzy rule while “Driving a Car”: “IF the distance to the car in front is small, AND the distance is decreasing slowly, THEN decelerate quite big” n The question that arises: Given a certain distance and a certain change of distance, what (crisp) value of acceleration should we select? President University Erwin Sitompul NNFL 8/8

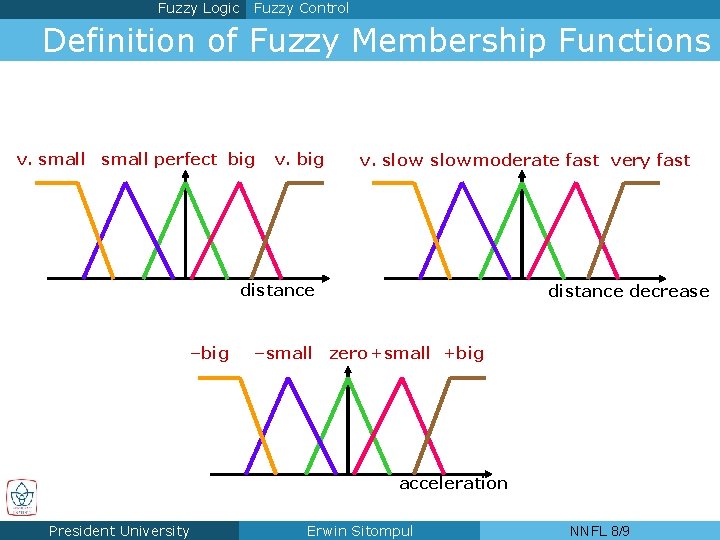
Fuzzy Logic Fuzzy Control Definition of Fuzzy Membership Functions v. small perfect big v. slow moderate fast very fast distance –big distance decrease –small zero +small +big acceleration President University Erwin Sitompul NNFL 8/9

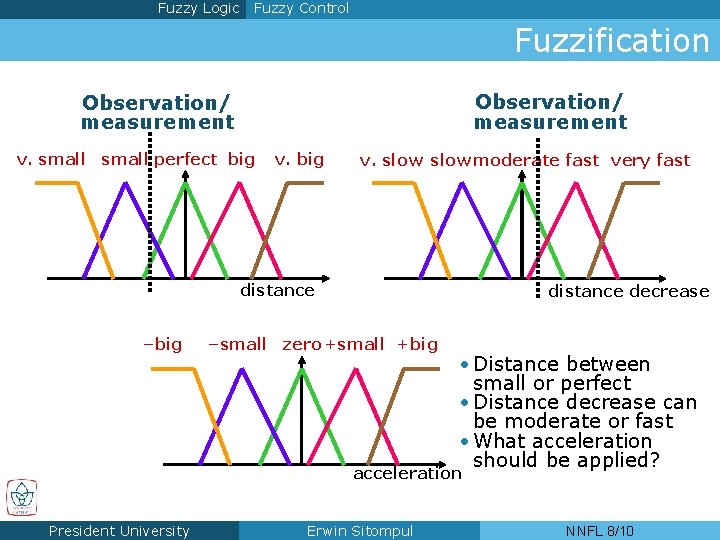
Fuzzy Logic Fuzzy Control Fuzzification Observation/ measurement v. small perfect big v. slow moderate fast very fast distance –big distance decrease –small zero +small +big • Distance between small or perfect • Distance decrease can be moderate or fast • What acceleration should be applied? acceleration President University Erwin Sitompul NNFL 8/10

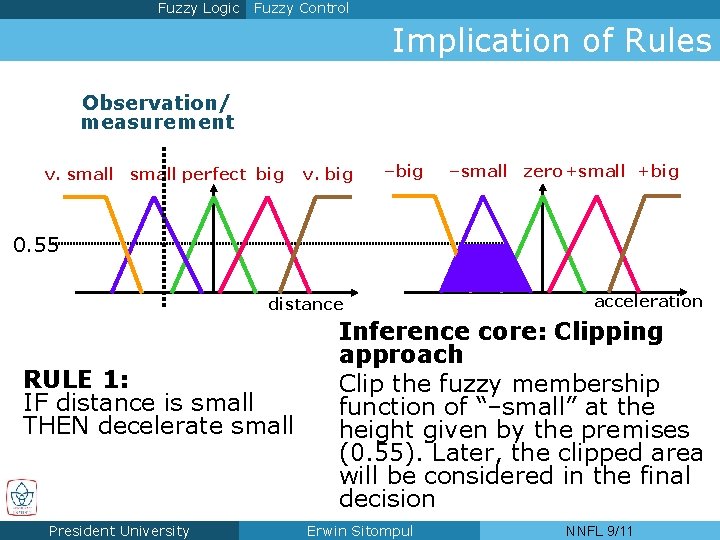
Fuzzy Logic Fuzzy Control Implication of Rules Observation/ measurement v. small perfect big v. big –small zero +small +big 0. 55 distance RULE 1: IF distance is small THEN decelerate small President University acceleration Inference core: Clipping approach Clip the fuzzy membership function of “–small” at the height given by the premises (0. 55). Later, the clipped area will be considered in the final decision Erwin Sitompul NNFL 9/11

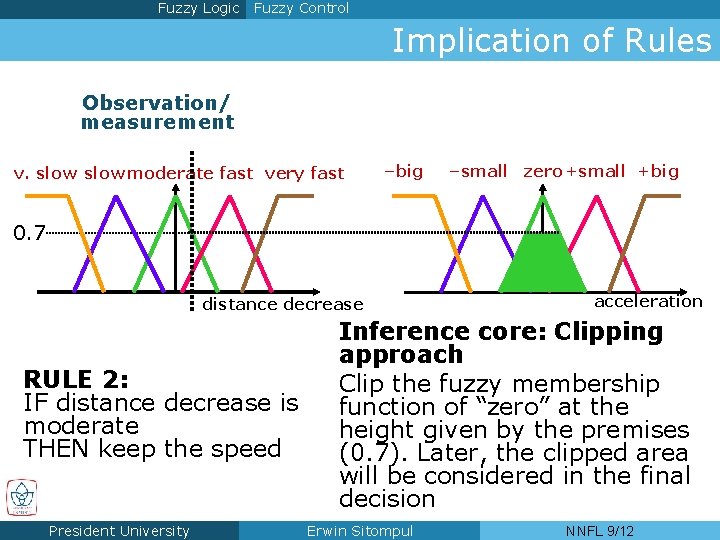
Fuzzy Logic Fuzzy Control Implication of Rules Observation/ measurement v. slow moderate fast very fast –big –small zero +small +big 0. 7 distance decrease RULE 2: IF distance decrease is moderate THEN keep the speed President University acceleration Inference core: Clipping approach Clip the fuzzy membership function of “zero” at the height given by the premises (0. 7). Later, the clipped area will be considered in the final decision Erwin Sitompul NNFL 9/12

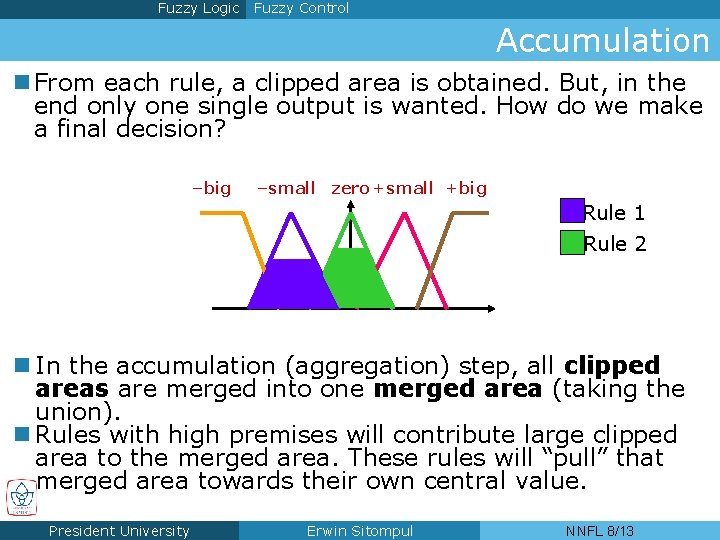
Fuzzy Logic Fuzzy Control Accumulation n From each rule, a clipped area is obtained. But, in the end only one single output is wanted. How do we make a final decision? –big –small zero +small +big Rule 1 Rule 2 acceleration n In the accumulation (aggregation) step, all clipped areas are merged into one merged area (taking the union). n Rules with high premises will contribute large clipped area to the merged area. These rules will “pull” that merged area towards their own central value. President University Erwin Sitompul NNFL 8/13

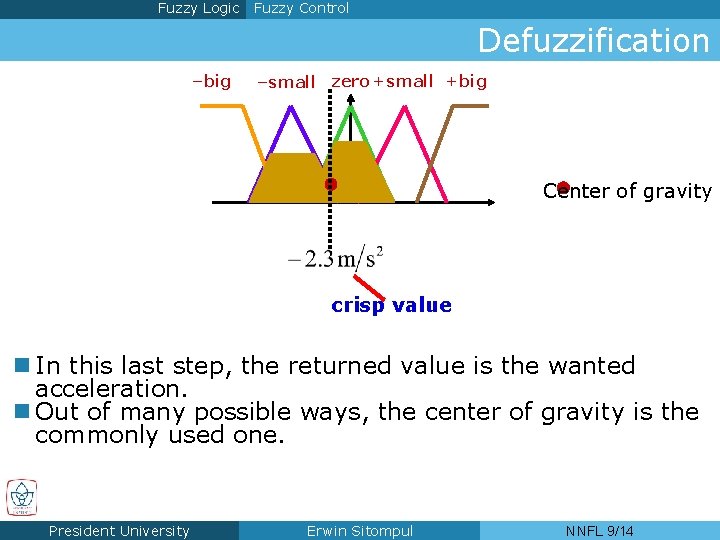
Fuzzy Logic Fuzzy Control Defuzzification –big –small zero +small +big acceleration Center of gravity crisp value n In this last step, the returned value is the wanted acceleration. n Out of many possible ways, the center of gravity is the commonly used one. President University Erwin Sitompul NNFL 9/14

Fuzzy Logic Fuzzy Control Inference Core n There are two approach for inference core: 1. Clipping approach: Min-Operator 0. 55 acceleration Membership function Fuzzification value 2. Scaling approach: 0. 55 Algebraic Product acceleration President University Erwin Sitompul NNFL 8/15

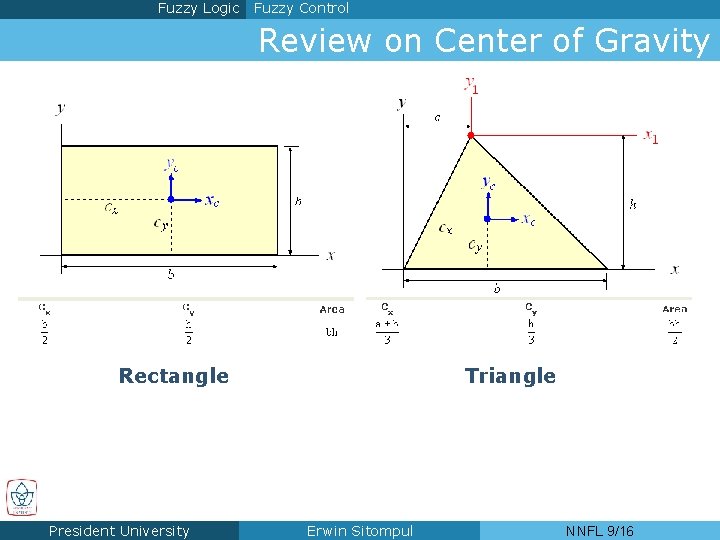
Fuzzy Logic Fuzzy Control Review on Center of Gravity Rectangle President University Triangle Erwin Sitompul NNFL 9/16

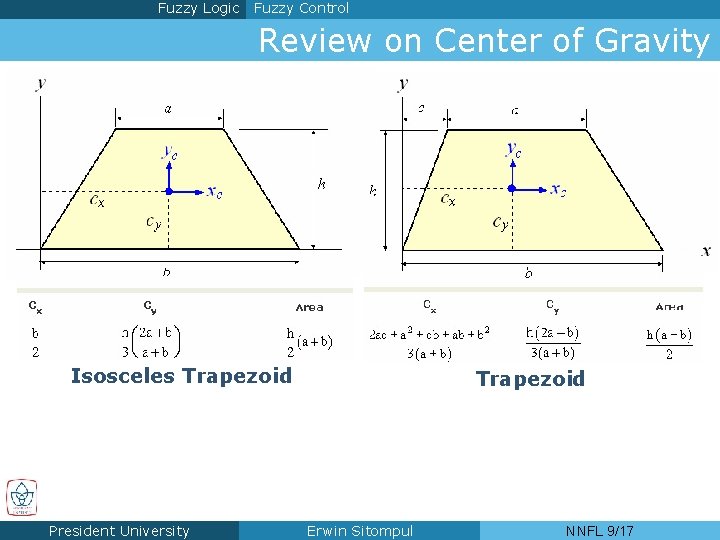
Fuzzy Logic Fuzzy Control Review on Center of Gravity Isosceles Trapezoid President University Trapezoid Erwin Sitompul NNFL 9/17

Fuzzy Logic Fuzzy Control Summary of Fuzzy Control 1. Fuzzify inputs, determine the degree of membership for all terms in the premise. 2. Apply fuzzy operators, if there are multiple terms in the premise (Min-Max, algebraic, bounded). 3. Apply inference core (clipping, scaling, etc. ) 4. Accumulate all outputs (union operation i. e. max, sum, etc. ) 5. Defuzzify (center of gravity of the merged outputs, max-method, modified center of gravity, height method, etc) President University Erwin Sitompul NNFL 8/18

Fuzzy Logic Fuzzy Control Limitations of Fuzzy Control n Definition and fine-tuning of membership functions need experience (covered range, number of MFs, shape). n Defuzzification may produce undesired results (needs redefinition of membership functions). President University Erwin Sitompul NNFL 8/19

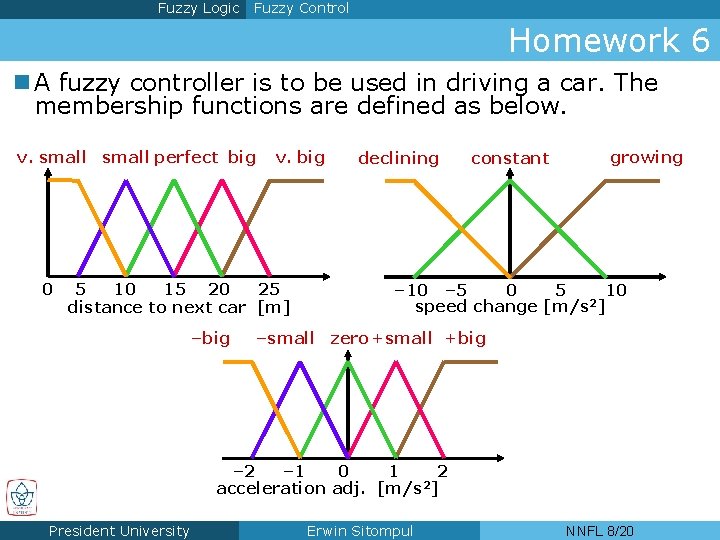
Fuzzy Logic Fuzzy Control Homework 6 n A fuzzy controller is to be used in driving a car. The membership functions are defined as below. v. small perfect big v. big declining constant growing 1 0 5 10 15 20 25 distance to next car [m] –big – 10 – 5 0 5 10 2 speed change [m/s ] –small zero +small +big 1 – 2 – 1 0 1 2 2 acceleration adj. [m/s ] President University Erwin Sitompul NNFL 8/20

Fuzzy Logic Fuzzy Control Homework 6 (Cont. ) n A fuzzy controller is to be used in driving a car. The membership functions are defined as below. Rule 1: IF distance is small AND speed is declining, THEN maintain acceleration. Rule 2: IF distance is small AND speed is constant, THEN acceleration adjustment negative small. Rule 3: IF distance is perfect AND speed is declining, THEN acceleration adjustment positive small. Rule 4: IF distance is perfect AND speed is constant, THEN maintain acceleration. President University Erwin Sitompul NNFL 8/21

Fuzzy Logic Fuzzy Control Homework 6 (Cont. ) n Using Min-Max as fuzzy operators, clipping as inference core, union operator as accumulator, and center of gravity method as defuzzifier, find the output of the controller if the measurements confirms that distance to next car is 13 m and the speed is increasing by 2. 5 m/s 2. President University Erwin Sitompul NNFL 8/22