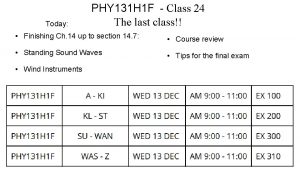
PHY 101 Lecture 1 1 1 The Nature












































- Slides: 51

PHY 101: Lecture 1 ► ► ► ► 1. 1 The Nature of Physics 1. 2 Units 1. 3 The Role of Units in Problem Solving 1. 4 Trigonometry 1. 5 Scalars and Vectors 1. 6 Vector Addition and Subtraction 1. 7 The Components of a Vector 1. 8 Addition of Vectors by Means of Components

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 1 The Nature of Physics

Physics - 1 Most fundamental physical science • Concerned with the fundamental principles of the Universe • • It is the foundation for engineering, technology, astronomy, biology, chemistry, and geology

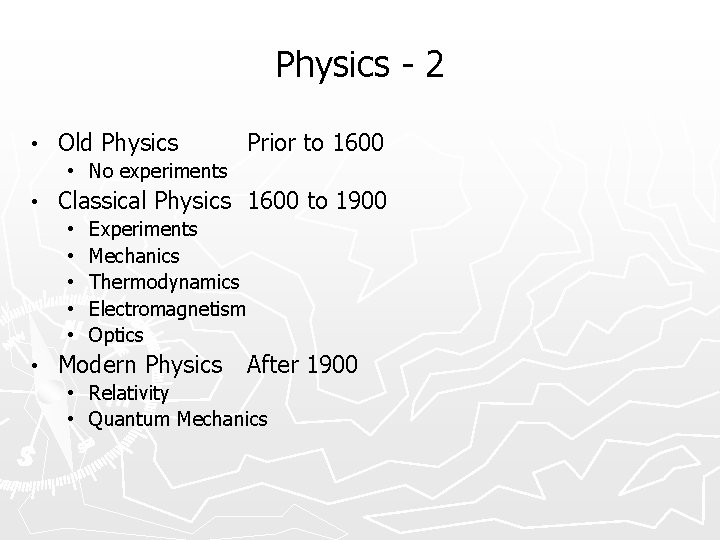
Physics - 2 • Old Physics Prior to 1600 • No experiments • Classical Physics 1600 to 1900 • • • Experiments Mechanics Thermodynamics Electromagnetism Optics Modern Physics After 1900 • Relativity • Quantum Mechanics

Physics - 3 • Classical physics (pre-1900): classical mechanics, electromagnetism, optics, thermodynamics • Galileo Galilei (1564– 1642): developed laws of motion with constant acceleration • Johannes Kepler (1571– 1630): developed empirical laws for the motions of planetary bodies • Isaac Newton (1642– 1727): developed classical mechanics as a systematic theory and was one of the originators of calculus • James Clerk Maxwell (1831– 1879): provided a unified theory of electromagnetism

Physics - 4 • Modern physics (at the end of the 19 th century) developed because many physical phenomena could not be explained by classical physics • Two most important developments: • theories of relativity • quantum mechanics

Physics - 5 • Albert Einstein’s theory of relativity: • completely revolutionized the traditional concepts of space, time, and energy • correctly describes the motion of objects moving at speeds comparable to the speed of light • theory shows that the speed of light is the upper limit of the speed of an object and that mass and energy are related • Quantum mechanics: • provides descriptions of physical phenomena at the atomic level

Physics - 6 Physics—based on experimental observations and mathematical analyses • Main objectives: • • to develop theories that explain phenomena • to relate theories to other established theories • Possible to explain behavior of physical systems using a few fundamental laws • laws expressed in the language of mathematics

Unifying Phenomena - 1 • • Stepping out of a row boat Rowing a boat Swimming Firing a gun Exploding fire works Flying a jet plane Pushing a friend while skating on ice Colliding cars Conservation of Momentum

Unifying Phenomena - 2 • • • Football padding Seat belts Air bags Styrofoam packing material Follow through when hitting a ball Moving hand, arm, body back when catching baseball line drive Change in Momentum Force vs. Time

Physics - 7 You live in the world • You know how the world works • “Physics is around you everyday But you do not recognize it”

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 2 Units

Units - 1 SI units (MKS) Ø meter (m) Ø kilogram (kg) Ø second (s) unit of length unit of mass unit of time CGS units Ø centimeter (cm) unit of length Ø gram (g) unit of mass Ø second (s) unit of time BE Units (British Engineering) § foot (ft) § slug (sl) § second (s) unit of length unit of mass unit of time

Length (meter) - 1 ► 1793 - France adopted the meter as 1/10, 000 of the distance from the North Pole to the equator along a line through Paris Ø Difficulty in making the measurement ► 1870 s - meter was distance between two scratch marks on a rod Ø Not portable Ø Creep (changes in length over time) Ø Width of marks limits accuracy of standard Ø Temperature dependency ► 1960 – 1, 650, 763. 73 wavelengths of red-orange Kryton-86 light ► 1986 - length in vacuum travelled by light in 1/299, 792, 458 s

Length (meter) - 2

Time (second) - 1 ► Originally, second was 1/86, 400 of the mean solar day ØMean solar day is gradually becoming longer at a variable rate ► 1967 - Duration of 9 x 109 wave cycles of radiation from a Cesium-133 atomic clock

Time (second) - 2

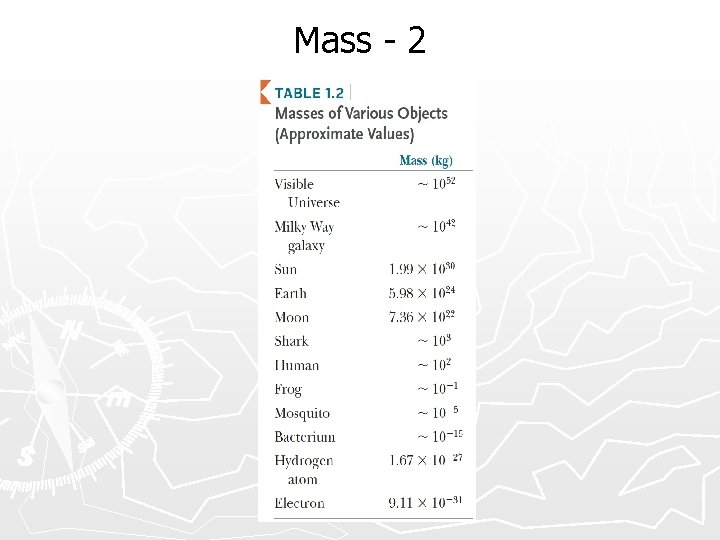
Mass (kilogram) - 1 ► 1795 - kilogram is mass of 1 liter of water ► 1799 - kilogram is a block of metal ØMass is increasing over time ØReason for this is a mystery

Mass - 2

Current Standard Kilogram

Inertial Mass - 1 ► Mass is amount of matter - not a useful definition ► Definitions of the kilogram are based on inertia and gravity ► Galileo (1564 - 1642) Ø Inertia is tendency of a mass to maintain motion Ø Force is necessary to change motion Ø Mass is a measure of inertia Ø Larger mass requires larger force for same change of motion

Inertial Mass - 2 ► How is mass determined using inertia? 1. 2. 3. 4. 5. 6. 7. Select a standard mass (ms) Apply a known force (F) Measure the acceleration of standard (as) Select an unknown mass (m) Apply the same known force (F) Measure the acceleration of unknown (a) Unknown mass is ► m = ms(as/a)

Gravitational Mass - 1 ► Newton (1643 – 1727) § Masses attract each other with force of gravity that is proportional to the mass ► Gravitational mass is defined using the gravitational force of the earth ► Experiments show that inertial and gravitational mass are the same within 1 x 109

Gravitational Mass - 2 ► How is mass determined using gravity? 1. Select a standard mass (ms) 2. Measure the weight of standard (ws) 3. Select an unknown mass (m) 4. Measure the weight of unknown (w) 5. Unknown mass is ►m = ms(w/ws)

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 3 The Role of Units in Problem Solving

Unit Conversion - Example 1 Example: Convert 3 feet to meters Unit analysis gives ► feet x (meter/feet) = meter Find conversion factor from front book cover ► 1 meter = 3. 281 feet ► divide both side of the equation by 3. 281 feet ► 1 meter / 3. 281 feet = 1 Place numbers in the unit analysis ► 3 feet x (1 meter/3. 281 feet) = 0. 9144 meters

Unit Conversion – Example 2 Example: Convert 60 mi/h to m/s Unit analysis gives Find conversion factors from front book cover ► 1 mi = 1609 m ► 1 = 1609 m / 1 mi ► 1 hr = 3600 s ► 1 = 3600 s / 1 h Place numbers in the unit analysis

Unit Conversion - Example 3 ► If unit increases (decreases), the number must decrease (increase) to keep quantity constant ØExample: ØConvert (0. 08 cm) to (x km) ØGoing from cm to km, the unit gets larger by 100, 000 ØTo keep the quantity in brackets constant, x has to be 100, 000 times smaller than 0. 08 Ø(0. 08/100, 000) (cm x 100, 000) = 8 x 10 -7 km

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 4 Trigonometry Skipped

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 5 Scalars and Vectors

Scalar Quantity ► Described by a single number ► The number gives the size or magnitude ► Examples: Øtemperature Øtime Ømass Øvolume

Vector Quantity ► ► ► Described by both magnitude and direction Arrows are used to represent vectors Direction of the arrow gives the direction of the vector Length of arrow is proportional to the magnitude of vector Examples: Ø Ø Ø Displacement Velocity Acceleration Force Momentum

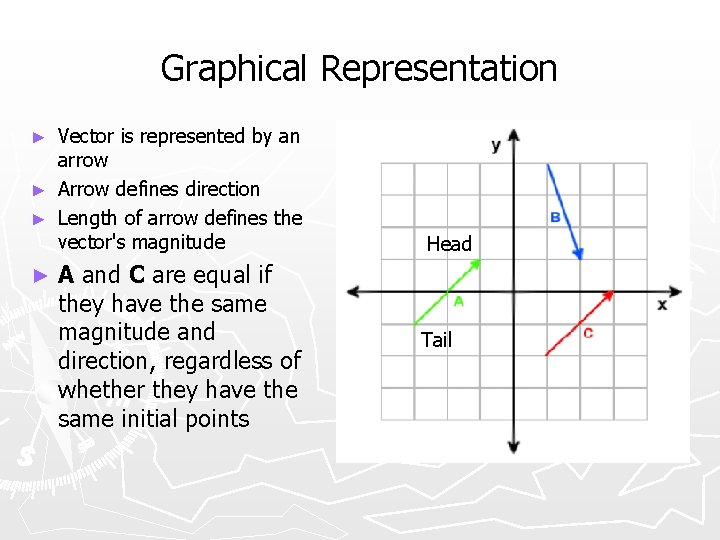
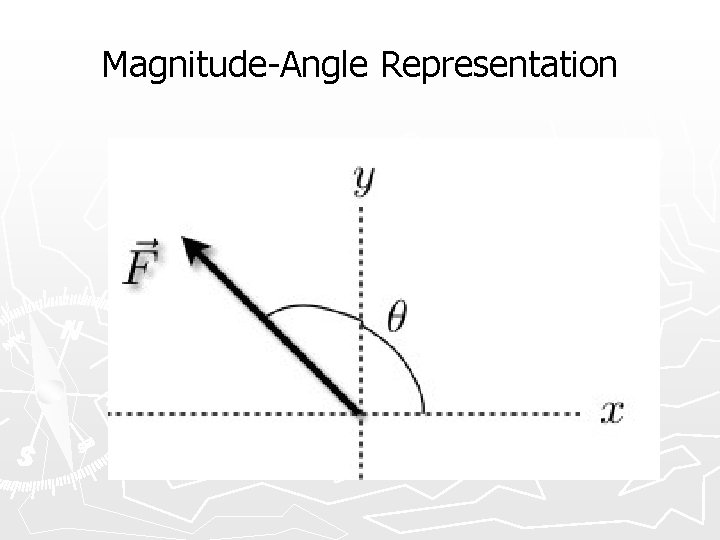
Vector Representation Vector A, can be represented in a number of ways ► Graphical Representation Ø Vector is an arrow ► Magnitude - Angle Representation Ø Give magnitude of vector and angle it makes with the xaxis Ø For example, magnitude |A| and angle q ► Component Representation Ø Give the x- and y-components of the vector Ø For example Ax, and Ay

Graphical Representation Vector is represented by an arrow ► Arrow defines direction ► Length of arrow defines the vector's magnitude ► ► A and C are equal if they have the same magnitude and direction, regardless of whether they have the same initial points Head Tail

Magnitude-Angle Representation

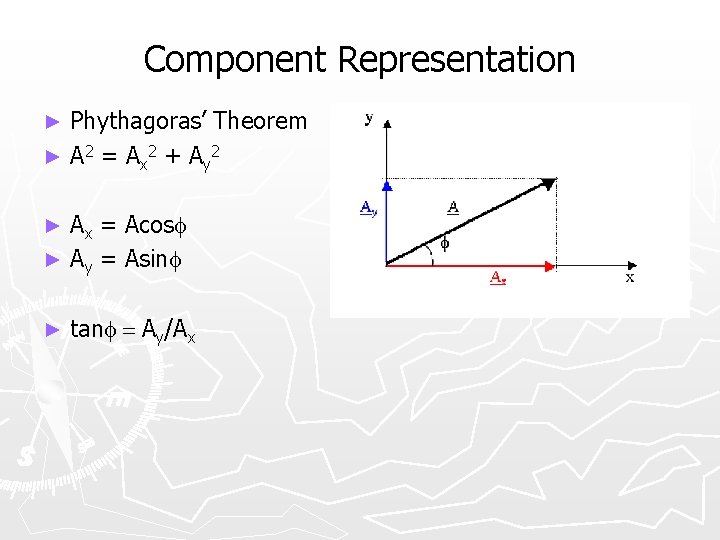
Component Representation Phythagoras’ Theorem ► A 2 = A x 2 + A y 2 ► Ax = Acosf ► Ay = Asinf ► ► tanf = Ay/Ax

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 6 Vector Addition and Subtraction

Vector Addition - Graphical ► Sum of two vectors is resultant vector, R. ► Method of Addition (R = A + B) ØPlace an arrow for vector A ØPlace the tail of the arrow for vector B at the head of the arrow for vector A ØResult, R, is the arrow with the tail at the tail of A and the head at the head of B

Vector Addition - Example 1 Vectors are in the same direction ► Magnitude of resultant is sum of magnitudes of the two vectors ► Direction of resultant is same as direction of the two vectors ► Example: ► Ø A is 275 m east Ø B is 125 m east Ø Magnitude of resultant is 275 m + 125 m = 400 m Ø Direction of the resultant is east

Vector Addition – Example 2 Vectors are perpendicular ► Magnitude of resultant is found using Pythagorean Theorem ► Angle is found using tan-1 ► Example: ► Ø Ø Ø A is 275 m east B is 125 m north Magnitude of resultant is Direction of the resultant is = tan-1(B/A) = tan-1(125/275) = 24. 40

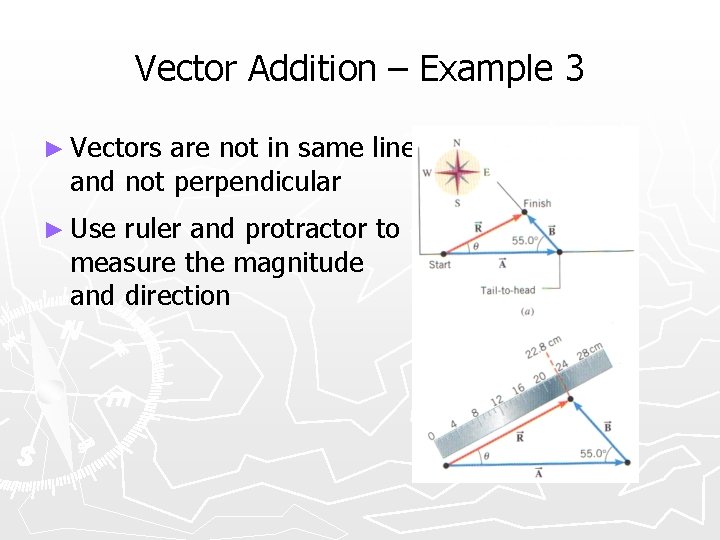
Vector Addition – Example 3 ► Vectors are not in same line and not perpendicular ► Use ruler and protractor to measure the magnitude and direction

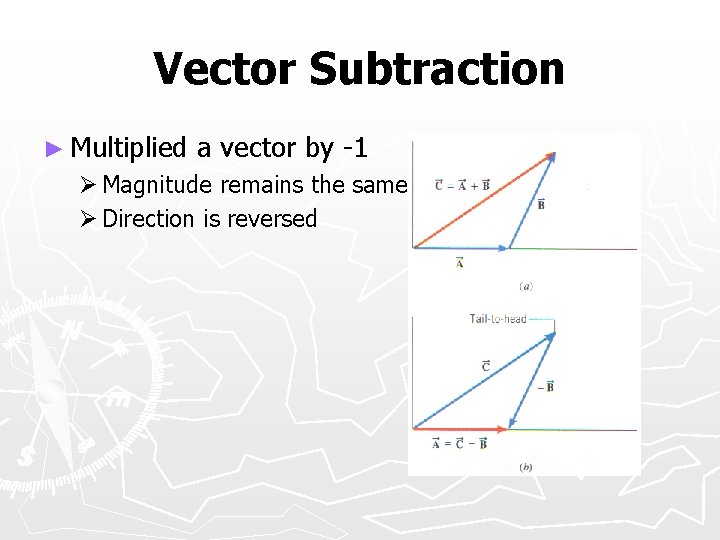
Vector Subtraction ► Multiplied a vector by -1 Ø Magnitude remains the same Ø Direction is reversed

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 7 The Components of a Vector

Vector Components ► Components of vector A Ø Two perpendicular vectors Ax and Ay that are parallel to the x and y axes and add together so that A = Ax + Ay

Vector Components - Example 1 ► Vector of magnitude 10 m at an angle of 300 to the +x-axis ► Components are: ØAx = 10 cos(30) = 10(0. 866) = 8. 66 m ØAy = 10 sin(30) = 10(0. 5) = 5. 0 m

Vector Components - Example 2 ► Vector X has a magnitude of 500 km, and angle of 400 to the +x-axis, Ø(a) What is the x-component, Xx? Ø(b) What is the y-component, Xy? ► (a) Xx = 500 cos(40) = 383. 0 km ► (b) Xy = 500 sin(40) = 321. 4 km

Vector Components - Example 3 ► Vector Y has x-component of -6. 0 m ► Vector Y has y-component of +7. 0 m ► In which quadrant is the vector? ØSince x is negative and y is positive, the vector points into the second quadrant

PHY 101: Lecture 1 Introduction and Mathematical Concepts 1. 8 Addition of Vectors by Means of Components

Vector Addition - Components ►C =A+B Ø Cx = A x + B x Ø Cy = A y + B y ►C ► = sqrt(Cx 2 + Cy 2)

Vector Addition – Components Example 1 ► Vector A has a magnitude of 10 km and an angle of 300 to the +x-axis ► Vector B has a magnitude of 20 km and an angle of 400 to the +x-axis ► (a) What is the x-component of the vector C = A + B? Ø Ax = 10 cos(30) = 8. 66 Bx = 20 cos(40) = 15. 32 Ø Cx = Ax + Bx = 8. 66 + 15. 32 = 23. 98 km ► (b) What is the y-component of the vector C = A + B? Ø Ay = 10 sin(30) = 5. 00 By = 20 sin(40) = 12. 86 Ø Cy = Ay + By = 5. 00 + 12. 86 = 17. 86 km ► (c) What is the magnitude of the vector C = A + B? Ø magnitude of C = sqrt(23. 982 + 17. 862) = 29. 90 km ► (d) What angle with the +x-axis is made by the vector C = A + B? Ø = tan-1(17. 86/23. 98) = 37. 70

Vector Addition – Components Example 2 Vector A has a magnitude of 10 km and an angle of 300 to the +x-axis ► Vector B has a magnitude of 20 km and an angle of 40 0 to the +x-axis ► (a) What is the x-component of the vector C = 2 A - B? ► Ø Ax = 10 cos(30) = 8. 66 Bx = 20 cos(40) = 15. 32 Ø Cx = 2 Ax - Bx = 2(8. 66) - 15. 32 = 2. 00 km ► (b) What is the y-component of the vector C = 2 A - B? Ø Ay = 10 sin(30) = 5. 00 By = 20 sin(40) = 12. 86 Ø Cy = 2 Ay - By = 2(5. 00) - 12. 86 = -2. 86 km ► (c) What is the magnitude of the vector C = 2 A - B? Ø magnitude of C = sqrt(2. 002 + 2. 862) = 12. 18 km ► (d) What angle with the +x-axis is made by the vector C = 2 A - B? Ø = tan-1(2. 86/2. 00) = 55. 00 below the +x-axis because of the signs on the components
 Transopia
Transopia 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Lecture 101
Lecture 101 Physics 101 lecture 1
Physics 101 lecture 1 Physics 101 lecture notes pdf
Physics 101 lecture notes pdf What is a harmonic wave in physics
What is a harmonic wave in physics Wave motion definition
Wave motion definition Phy 132
Phy 132 Phy
Phy Rotational statics
Rotational statics Applications of magnetism
Applications of magnetism Phy
Phy Phy 205
Phy 205 Ddr phy architecture
Ddr phy architecture Phy 212
Phy 212 Phy 131 past papers
Phy 131 past papers Phy
Phy Phy
Phy Phy 1214
Phy 1214 Phy theorem
Phy theorem 2012 phy
2012 phy Phy 2049
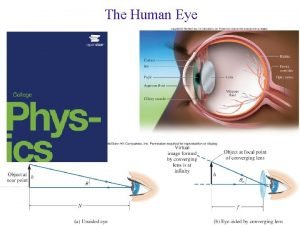
Phy 2049 Accommodation eye
Accommodation eye Phy 1214
Phy 1214 Law of motion
Law of motion Pa msu
Pa msu Life phy
Life phy Phy
Phy Phy 108
Phy 108 Phy-105 5 discussion
Phy-105 5 discussion Phy113
Phy113 General physics
General physics Phy 2049
Phy 2049 Phy 1214
Phy 1214 Phy
Phy Phy theorem
Phy theorem Phy circuit
Phy circuit Atm packet phy
Atm packet phy Phy tgen
Phy tgen Phy 121 asu
Phy 121 asu Loncapa fsu
Loncapa fsu Phy 1214
Phy 1214 Phy
Phy Nature and nature's law lay hid in night
Nature and nature's law lay hid in night Nature nature controversy
Nature nature controversy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Lp html
Lp html Hệ hô hấp
Hệ hô hấp So nguyen to
So nguyen to Tư thế ngồi viết
Tư thế ngồi viết đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới