PHY 101 Lecture 2 2 1 Displacement 2

PHY 101: Lecture 2 • • 2. 1 Displacement 2. 2 Speed and Velocity 2. 3 Acceleration 2. 4 Equations of Kinematics for Constant Acceleration 2. 5 Applications of the Equations of Kinematics 2. 6 Freely Falling Bodies 2. 7 Graphical Analysis of Velocity and Acceleration

PHY 101: Lecture 2 Kinematics in One Dimension 2. 1 Displacement

Kinematics Definition of Distance • Type of Quantity: Scalar • Total path length traversed in moving from one position to another • Distance depends on path and not on starting and ending points • Symbol: d • SI Unit: meter (m)

Kinematics Distance - Example • What is the distance for each of the following trips? Ø 1. 3 m east, 4 m east Ø 2. 3 m east, 4 m north Ø 3. 3 m east, 4 m west • For each trip, the distance is 7 m

Xi Definition of Initial Position • Type of Quantity: Vector • Initial position of an object is indicted by a position vector, xi, from the origin to the position xi • Magnitude of xi is distance from the origin to position xi • Direction of xi is either + or • Symbol: xi • SI Unit: meter (m) • Note: Subscript f means the final position, xf xi xi

2 -Dimensional Example Position / Free Vectors

Definition of Displacement • Type of Quantity: Vector • Vector drawn from initial position to final position Ø xi + Dx = xf Ø Dx = xf - xi • Magnitude equals shortest distance between initial and final positions Xi • Direction points from initial to final position • Displacement depends on the initial and final positions and not on path length • Symbol: Dx • SI Unit: meter (m) § D is always final value minus initial value DX Xf

Distance / Displacement

Direction of Displacement • Vector nature of displacement is giving by Ø+ sign to indicate displacement in the +x direction, to the right, or east Ø- sign to indicate displacement in the –x direction, to the left, or west • Note: The same is true for position, velocity, and acceleration

Example of + / - Sign • 500 meters in the +x direction is +500 meters • 500 meters in the –x direction is -500 meters

Distance vs. Displacement • An object can move so that the path length (distance) is large but the displacement is zero or small

Displacement – Example 1 • What is the displacement for each of the following situations? Ø 1. 3 m east, 4 m east » Displacement is 7 m east Ø 2. 3 m east, 4 m north » Displacement is 5 m at 530 above +x axis Ø 3. 3 m east, 4 m west » Displacement is 1 m west

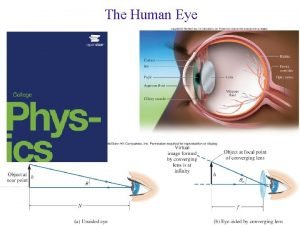
Displacement – Example 2 • A student throws a rock straight upward from shoulder level, which is 1. 65 m above the ground • What is the displacement of the rock when it hits the ground? Ø Displacement is a vector that points from the initial position to the final position Ø Initial position is 1. 65 m above the ground Ø Final position is the ground, height 0 m Ø Magnitude of the displacement vector is then 1. 65 m Ø Direction of the displacement vector is downward

PHY 101: Lecture 2 Kinematics in One Dimension 2. 2 Speed and Average Velocity

Definition of Average Speed • Type of Quantity: Scalar • Average Speed = Distance / Time • savg = d / t • Symbol: savg • SI Unit: meter/s (m/s)

What Does Constant Speed Mean? • Ball has initial position xi = 0 m at time ti = 0 • Ball has constant velocity t = 5 m/s • This means that during: Ø 1 st second ball moves 5 m Ø 2 nd second ball moves 5 m Ø 3 rd second ball moves 5 m, and so on … • Position at time t is: Ø t = 0 s, x = 0 m Ø t = 1 s, x = 5 m Ø t = 2 s, x = 10 m Ø t = 3 s, x = 15 m

Average Speed – Example 1 • A race car circles 10 times around an 8 -km track in 1200 s • What is its average speed in m/s? Ødistance traveled is d = 10 x 8 km = 80, 000 m Øt = 1200 s Øsavg = d/t = 80000 / 1200 s = 66. 7 m/s

Average Speed – Example 2 • A motorist drives 150 km from one city to another in 2. 5 h, but makes the return trip in only 2. 0 h • What are the average speeds for Ø (a) Ø (b) each half of the round-trip, and the total trip? • (a) Ø Ø First half of trip average speed = d/t = 150 km/2. 5 h = 60 km/h Second half of trip average speed = d/t = 150 km/2 h = 75 km/h • (b) Ø Entire trip Ø average speed is d/t = (150+150) / (2. 5 + 2) = 66. 67 km/h

Definition of Average Velocity • Type of Quantity: Vector • Average Velocity = Displacement / Time • vavg = Dx/t = (xf – xi)/t • Direction is the same as the direction of displacement • Symbol: vavg • SI Unit: meter/second (m/s)

Average Velocity – Example 1 • A race car circles 10 times around an 8 -km track in 1200 s • What is its average velocity in m/s ØAfter 10 laps, the ending position is the same as the starting position ØTherefore, displacement is zero, even though distance is 80, 000 m ØSince displacement is zero, average velocity is zero.

Average Velocity – Example 2 • Car travels half a lap in 3 seconds along a circle with radius = 150 m • (a) What is the distance traveled by the car? • Distance is the path length = half the circumference of the circle – d = 2 pr/2 = p(150) = 471 m • (b) What is the magnitude of the car’s displacement? – Displacement is the vector from the initial position to the final position – Vector is across the diameter of the circle – Magnitude of displacement is 2 x 150 = 300 m • (c) What is the average speed of the car? – Average speed s = distance / time = 471. 24 m / 3 s = 157 m/s • (d) What is the magnitude of the average velocity of the car? – Average velocity = displacement / time = 300 m / 3 s = 100 m/s

Average Velocity – Example 3 • A car travels a full lap in 5 seconds along a circle that has a radius of 150 m? • (a) What is the distance traveled by the car? • Distance is the path length = circumference of the circle • d = 2 pr = 2 p(150) = 942 m • (b) What is the magnitude of the car’s displacement? • Displacement is vector from the initial position to the final position • The initial and final positions are at the same location • Magnitude of displacement vector is zero. • (c) What is the average speed of the car? • Average speed s = distance / time = 942. 48 m / 5 s = 189 m/s • (d) What is magnitude of the average velocity of car? • Average velocity = displacement / time = 0 m / 5 s = 0 m/s

PHY 101: Lecture 2 Kinematics in One Dimension 2. 3 Acceleration

Definition of Average Acceleration • Type of Quantity: Vector • Acceleration = Change in Velocity / Time • aavg = Dv/t = (vf – vi)/t • Symbol: aavg • SI Unit: meter/second 2 (m/s 2) • Note: When velocity and acceleration have opposite direction (signs), the object is decelerating

Average Acceleration – Example 1 • An automobile traveling at 8 m/s along a straight, level road accelerates to 20 m/s in 6. 00 s • What is the magnitude of the auto’s average acceleration? Øaverage acceleration = Ø(vf – vi)/t = (20 – 8) / 6 = 2 m/s 2

Average Acceleration – Example 2 • Motorcycle has a constant acceleration of 2. 5 m/s 2 • Both the velocity and acceleration of the motorcycle point in the same direction • How much time is required for the motorcycle to change its velocity from 21 to 31 m/s. Ø aavg = (vf – vi) / t Ø 2. 5 m/s 2 = (31 m/s – 21 m/s) / t Ø t = 10 / 2. 5 = 4 s

PHY 101: Lecture 2 Kinematics in One Dimension 2. 4 Equations of Kinematics for Constant Acceleration

Equation of Motion • Equations that give x, v, and a as functions of t Ø x = f(t) Ø v = g(t) Ø a = h(t) • We will look at a special case where a is constant Ø a = aavg = constant independent of time • We can also eliminate t from x and v to obtain Ø v = j(x)

Development of Equations of Motion • a = aavg = (vf – vi) / t • vf = vi + at (constant acceleration) • vavg = (xf – xi) / t • xf = xi + vavgt • vavg = ½ (vf + vi) (constant acceleration)

Equations of Motion • vf = vi + at • xf = xi + vit + (1/2)at 2 • vf 2 = vi 2 + 2 a(xf – xi) • These are vector equations • xi, xf, vi, vf, a, and t can be + or -

Scalar vs. Vector Magnitude • Scalar can be negative or positive – For example, temperature, work, and energy can be negative or positive • Magnitude of a vector is always positive – For example, displacement, velocity, and acceleration magnitude is always positive • Negative sign on a magnitude is an indication that the vector points in the negative (opposite) direction

PHY 101: Lecture 2 Kinematics in One Dimension 2. 5 Applications of the Equations of Kinematics

Equations of Motion – Example 1 • • Basketball player starts from rest and accelerates uniformly to speed 6. 0 m/s in 1. 5 s What distance does the player run? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = ? vi = 0 vf = 6. 0 a = ? t = 1. 5 6=0+a(1. 5) Equation has a (1 st) xf=0+0(1. 5)+½a(1. 5)2 Equation has 2 unknowns, xf, a (2 nd) 62=02+2 a(xf– 0) Equation has two unknowns, xf, a 6=0+a(1. 5); a = 6/1. 5 = 4 m/s 2 xf=0+0(1. 5)+½(4)(1. 5)2 = 4. 5 m/s

Equations of Motion–Example 2 a • Car accelerates from rest at rate of 2. 0 m/s 2 for 5. 0 s • (a) What is the speed of the car at the end of that time? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = ? vi = 0 vf = ? a = 2. 0 t = 5. 0 vf=0+2(5) xf=0+0(5)+½(2)(5)2 vf 2=02+2(2)(xf– 0) vf=0+2(5)=10 m/s Equation has vf Equation has xf Equation has two unknowns, xf, vf

Equation of Motion – Example 2 b • Car accelerates from rest at rate of 2. 0 m/s 2 for 5. 0 s • (b) How far does the car travel in this time? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = ? vi = 0 vf = 10 a = 2. 0 t = 5. 0 10=0+2(5) Can’t use Equation xf=0+0(5)+½(2)(5)2 Equation has xf 102=02+2(2)(xf– 0)Equation has xf xf=0+0(5)+½(2)(5)2 = 25 m

Equation of Motion – Example 3 a • A car traveling at 15 m/s stops in 35 m • (a) What is the acceleration? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = 35 vi = 15 vf = 0 a = ? t=? 0=15+at 35=0+15 t+½(a)(t)2 02=152+2 a(35– 0) a = -225/70 = -3. 2 m/s 2 Equation has a, t Equation has a

Motion – Example 3 b • A car traveling at 15 m/s stops in 35 m • (b) What is time during this deceleration until car stops? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = 35 vi = 15 vf = 0 a = -3. 2 t = ? 0=15 -3. 2 t 35=0+15 t+½(-3. 2)(t)2 02=152+2(-3. 2)(35– 0) 0=15 -3. 2 t t = -15/-3. 2 = 4. 67 s Equation has t Can’t use equation

Equation of Motion – Example 4 • A plane accelerates at 8 m/s 2 on a runway that is 500 m long • The take off speed of the plane is 80 m/sec • Can the plane takeoff? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = 500 vi = 0 vf = ? a=8 t=? vf=0+8 t Equation has vf, t 500=0+0 t+½(8)(t)2 Equation has t vf 2=02+2(8)(500– 0) Equation has vf 2=02+2(8)(500– 0) = 500(16) vf=sqrt(500(16) = 89. 4 m/s • The plane can takeoff

Equation of Motion – Example 5 • A plane accelerates at 8 m/s 2 • The take off speed of the plane is 80 m/sec • What is minimum length of run way for plane to reach take off speed? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = ? vi = 0 vf = 80 a = 8 t=? 80=0+8 t xf=0+0 t+½(8)(t)2 802=02+2(8)(xf– 0) xf=6400/16 = 400 m Equation has t Equation has xf, t Equation has xf

Eq. of Motion – Example 6 Bull • • Bull runs 8 m/sec A boy at rest has a head start of 12 m When he sees the bull he accelerates at 2 m/s 2 Does the bull catch the boy? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 0 xf = ? vi = 8 vf = 8 a = 0 t = ? 8=8+0 t Can’t use this equation xf=0+8 t+½(0)(t)2 Equation has xf, t 82=82+2(0)(xf– 0) Can’t use this equation

Eq. of Motion – Example 6 Boy • • Bull runs 8 m/sec A boy at rest has a head start of 12 m When he sees the bull he accelerates at 2 m/s 2 Does the bull catch the boy? vf = vi + at xf = xi + vit + ½at 2 vf 2 = vi 2 + 2 a(xf – xi) xi = 12 xf = ? vi = 0 vf = ? a = 2 t=? vf=0+2 t Equation has vf, t xf=12+0 t+½(2)(t)2 Equation has xf, t vf 2=02+2(2)(xf– 12) Equation has xf, vf

Example 6 Bull / Boy • • Bull runs 8 m/sec A boy at rest has a head start of 12 m When he sees the bull he accelerates at 2 m/s 2 Does the bull catch the boy? xf=0+8 t+½(0)(t)2 (from Bull equations) xf=12+0 t+½(2)(t)2 (from Boy equations) They catch up to each other when the boy xf = bull xf 8 t=12+t 2 t 2 -8 t+12=0 Factor (t-2)(t-6) = 0 • Bull catches boy at 2 s and 6 s • 2 s is bull catching up to the boy • 6 s is the accelerating boy catching up to the bull

PHY 101: Lecture 2 Kinematics in One Dimension 2. 6 Freely Falling Bodies

Free Fall • • Objects falling vertically Near the surface of the earth Acceleration due to gravity a = -9. 8 m/s 2

Free Fall – Example 1 • A bomb is dropped from 6000 m • With what speed does it hit the ground? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 6000 yf = 0 vi = 0 vf = ? a = -9. 8 t=? vf = 0 – 9. 8 t 0 = 6000 + 0 t + ½ (-9. 8)t 2 vf 2 = 02 + 2(-9. 8) (0 – 6000) vf 2 = 02 + 2(-9. 8)(-6000) vf = sqrt(117600) = -343 m/s Equation has vf, t Equation has vf

Free Fall – Example 2 a • A student drops a ball from the top of a tall building • It takes 2. 8 s for the ball to reach the ground • (a) What is the height of the building? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = ? yf = 0 vi = 0 vf = ? a = -9. 8 t = 2. 8 vf = 0 – 9. 8(2. 8) Equation has vf 0 = yi + 0(2. 8) + ½(-9. 8)(2. 8)2 Equation has yi vf 2 = 02 + 2(-9. 8) (0 – yi) Equation has yi, vf 0 = yi + (1/2)(-9. 8)(2. 8)2 yi = 38. 4 m

Free Fall – Example 2 b • A student drops a ball from the top of a tall building • It takes 2. 8 s for the ball to reach the ground • (b) What was the ball’s velocity just before hitting the ground? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 38. 4 yf = 0 vi = 0 vf = ? a = -9. 8 t = 2. 8 vf = 0 – 9. 8(2. 8) Equation has vf 0 = 38. 4 + 0(2. 8) + ½(-9. 8)(2. 8)2 Can’t use equation vf 2 = 02 + 2(-9. 8) (0 – 38. 4) Equation has vf = 0 – 9. 8(2. 8) = -27. 4 m/s (- means downward)

Free Fall – Example 3 • Boy throws stone straight upward with an initial velocity of 15 m/s • What maximum height will stone reach before falling back down? • At the maximum height vy = 0 vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = ? vi = 15 vf = 0 a = -9. 8 t=? 0 = 15 – 9. 8 t Equation has t yf = 0 + 15 t + ½(-9. 8)t 2 Equation has yf, t 02 = 152 + 2(-9. 8) (yf – 0) Equation has yf 02 = 152 + 2(-9. 8) (yf – 0) yf = -152/2/-9. 8 = 11. 48 m

Free Fall – Example 4 • Ball thrown upwards at 40 m/s. Calculate time to reach 35 m vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = 35 vi = 40 vf = ? a = -9. 8 t=? vf = 40 – 9. 8 t Equation has vf, t (2 nd) 35 = 0 + 40 t + ½(-9. 8)t 2 Equation has t vf 2 = 402 + 2(-9. 8) (35 – 0) Equation has vf (1 st) vf 2 = 402 + 2(-9. 8) (35 – 0) = 914 vf = +30. 2 or -30. 2 = 40 – 9. 8 t t = (30. 2 – 40) / (-9. 8) = 1. 0 s (time on the way up)

Free Fall – Example 5 Ball 1 • A ball is dropped from rest • Four seconds later, a second ball is thrown down at 50 m/s Calculate when and where the two balls meet vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = ? vi = 0 vf = ? a = -9. 8 t=? vf = 0 – 9. 8 t yf = 0 + 0 t + ½(-9. 8)t 2 vf 2 = 02 + 2(-9. 8) (yf – 0) Equation has vf, t Equation has yf, vf

Free Fall – Example 5 Ball 2 • A ball is dropped from rest • Four seconds later, a second ball is thrown down at 50 m/s Calculate when and where the two balls meet vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 0 yf = ? vi = -50 vf = ? a = -9. 8 t=t– 4? vf = -50– 9. 8(t-4) yf = 0 -50(t-4)+½(-9. 8)(t-4)2 vf 2 = 502+2(-9. 8) (yf – 0) Equation has vf, t Equation has yf, vf

Free Fall – Example 5 Balls 1 and 2 • A ball is dropped from rest • Four seconds later, a second ball is thrown down at 50 m/s • Calculate when and where two balls meet yf = 0 + 0 t + ½(-9. 8)t 2 (from ball 1) yf = 0+50(t-4)+½(-9. 8)(t-4)2 (from ball 2) Substitute equation 1 into equation 2 -4. 9 t 2 = -50(t-4) – 4. 9(t-4)2 -4. 9 t 2 = -50 t + 200 – 4. 9 t 2 +39. 4 t – 78. 4 -10. 6 t + 121. 6 = -0 t = -121. 6 / -10. 6 = 11. 4 s

Free Fall – Example 6 a • From tower 100 m high, ball is thrown up with speed of 40 m/s • (a) How high does it rise? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 100 yf = ? vi = 40 vf = 0 a = -9. 8 t=? 0 = 40 – 9. 8 t Equation has t yf = 100 + 40 t + ½(-9. 8)t 2 Equation has yf, t 02 = 402+2(-9. 8)(yf– 100) Equation has yf 02 = 402+2(-9. 8)(yf– 100) yf = (-1600/2/-9. 8) + 100 = 181. 6 m

Free Fall – Example 6 b • From tower 100 m high, ball is thrown up with speed of 40 m/s • (b) When does it hit ground? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 100 yf = 0 vi = 40 vf = ? a = -9. 8 t=? vf = 40 – 9. 8 t Equation has vf, t 0 = 100 + 40 t + ½(-9. 8)t 2 Equation has t vf 2 = 402+2(-9. 8)(0– 100) Equation has vf 0 = 100 + 40 t + ½(-9. 8)t 2 -4. 9 t 2 + 40 t + 100 = 0 (Use quadratic equation) t = 10. 2 s

Free Fall – Example 6 c • From tower 100 m high, ball is thrown up with speed of 40 m/s • (c) How fast is it moving at the ground ? vf = vi + at yf = yi + vit + ½at 2 vf 2 = vi 2 + 2 a(yf – yi) yi = 100 yf = 0 vi = 40 vf = ? a = -9. 8 t = 10. 2 vf = 40 – 9. 8(10. 2) Equation has vf 0 = 100+40(10. 2)+½(-9. 8)(10. 2)2 Can’t use equation vf 2 = 402+2(-9. 8)(0– 100) Equation has vf 2 = 402+2(-9. 8)(0– 100) = 1600 + 1960 = 3560 vf = -59. 7 m/s

PHY 101: Lecture 2 Kinematics in One Dimension 2. 7 Graphical Analysis of Velocity and Acceleration

Graphical Analysis 1 • Velocity = 0 Acceleration = 0 • Horizontal line on P-T graph: velocity = 0 Time 0 1 2 3 4 5 Pos 5 5 5

Graphical Analysis 2 • Velocity = 1 Acceleration = 0 • Sloping line on P-T graph: velocity <> 0 Time 0 1 2 3 4 5 Pos 0 1 2 3 4 5

Graphical Analysis 3 • Velocity = 2 Acceleration = 0 • Steeper slope means greater velocity Time 0 1 2 3 4 5 Pos 0 2 4 6 8 10

Graphical Analysis 4 • Velocity = -1 Acceleration = 0 • Negative slope means velocity in opposite direction Time 0 1 2 3 4 5 Pos 0 -1 -2 -3 -4 -5

Graphical Analysis 5 • Velocity = 1 Acceleration = 1 • Curving line on P-T graph: acceleration <> 0 Time 0 1 2 3 4 5 Pos 0 1. 5 4 7. 5 12 17. 5

Speed vs Average Speed (Charts) Time (min) Position (m) Time (min) Speed (m/min) 0 0 1 400 0. 5 400 2 1200 1. 5 800 3 2700 2. 5 1500 4 2900 3. 5 200 5 2900 4. 5 0 6 4000 5. 5 1100 7 5500 6. 5 1500 8 7200 7. 5 1700 9 7300 8. 5 100

Speed vs. Avg. Speed (Graphs)

Speed vs. Average Speed • Prior charts & graphs show trip of car • During trip the velocity changes • Average velocity remains constant during the trip • Average velocity produces same final position as does the varying velocity