EECS 274 Computer Vision Linear Filters and Edges

EECS 274 Computer Vision Linear Filters and Edges

Linear filters and edges • • Linear filters Scale space Gaussian pyramid and wavelets Edges • Reading: Chapters 7 and 8 of FP, Chapter 3 of S

Linear filters • General process: – Form new image whose pixels are a weighted sum of original pixel values, using the same set of weights at each point. • Properties – Output is a linear function of the input – Output is a shift-invariant function of the input (i. e. shift the input image two pixels to the left, the output is shifted two pixels to the left) • Example: smoothing by averaging – form the average of pixels in a neighbourhood • Example: smoothing with a Gaussian – form a weighted average of pixels in a neighbourhood • Example: finding a derivative – form a weighted average of pixels in a neighbourhood

Convolution • Represent these weights as an image, H • H is usually called the kernel • Operation is called convolution • Notation in textbook: – it’s associative • Notice wierd order of indices – all examples can be put in this form – it’s a result of the derivation expressing any shift-invariant linear operator as a convolution.

Example: smoothing by averaging

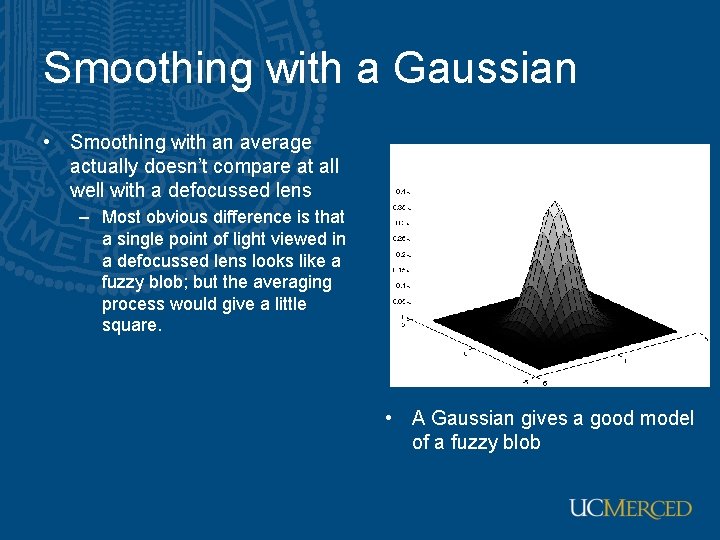
Smoothing with a Gaussian • Smoothing with an average actually doesn’t compare at all well with a defocussed lens – Most obvious difference is that a single point of light viewed in a defocussed lens looks like a fuzzy blob; but the averaging process would give a little square. • A Gaussian gives a good model of a fuzzy blob

An isotropic Gaussian • The picture shows a smoothing kernel proportional to (which is a reasonable model of a circularly symmetric fuzzy blob)

Smoothing with a Gaussian

Differentiation and convolution • Recall • Now this is linear and shift invariant, so must be the result of a convolution • We could approximate this as (which is obviously a convolution; it’s not a very good way to do things, as we shall see)

Finite differences Partial derivative in y axis, respond strongly to horizontal edges Partial derivative in x axis, respond strongly to vertical edges

Spatial filter • Approximation

Roberts operator One of the earliest edge detection algorithm by Lawrence Roberts

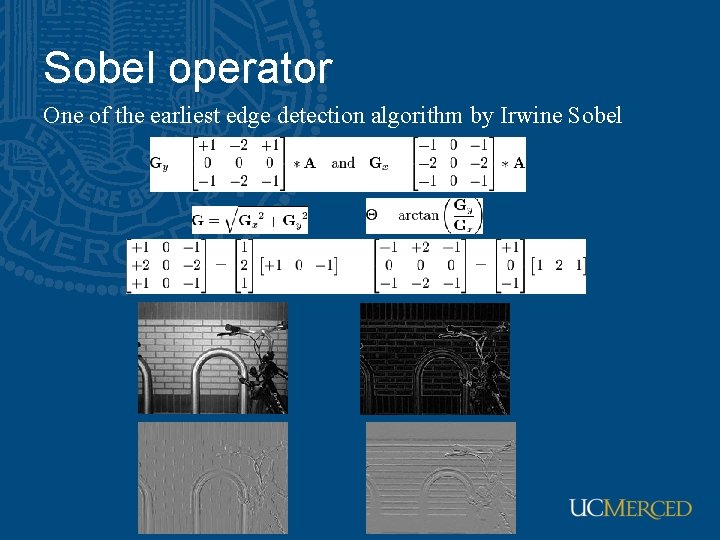
Sobel operator One of the earliest edge detection algorithm by Irwine Sobel

Noise • Simplest noise model – independent stationary additive Gaussian noise – the noise value at each pixel is given by an independent draw from the same normal probability distribution • Issues – this model allows noise values that could be greater than maximum camera output or less than zero – for small standard deviations, this isn’t too much of a problem - it’s a fairly good model – independence may not be justified (e. g. damage to lens) – may not be stationary (e. g. thermal gradients in the ccd)

sigma=1

sigma=16

Finite differences and noise • Finite difference filters respond strongly to noise – obvious reason: image noise results in pixels that look very different from their neighbours • Generally, the larger the noise the stronger the response • What is to be done? – intuitively, most pixels in images look quite a lot like their neighbours – this is true even at an edge; along the edge they’re similar, across the edge they’re not – suggests that smoothing the image should help, by forcing pixels different to their neighbours (=noise pixels? ) to look more like neighbours

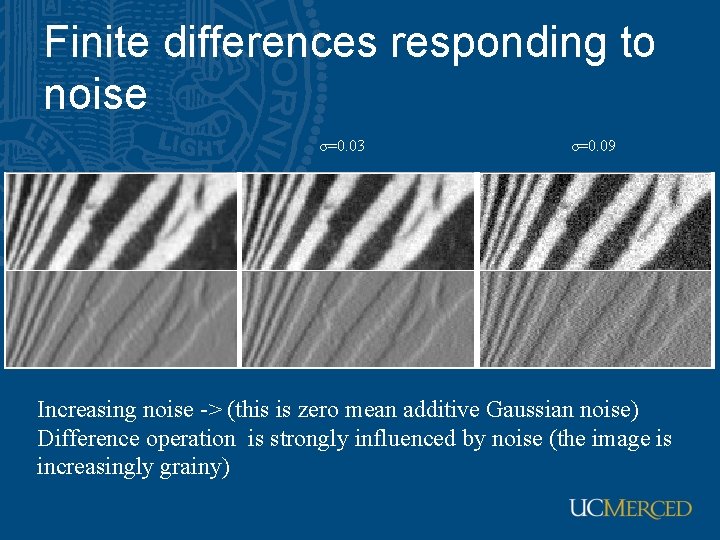
Finite differences responding to noise σ=0. 03 σ=0. 09 Increasing noise -> (this is zero mean additive Gaussian noise) Difference operation is strongly influenced by noise (the image is increasingly grainy)

The response of a linear filter to noise • Do only stationary independent additive Gaussian noise with zero mean (non-zero mean is easily dealt with) • Mean: – output is a weighted sum of inputs – so we want mean of a weighted sum of zero mean normal random variables – must be zero • Variance: – recall • variance of a sum of random variables is sum of their variances • variance of constant times random variable is constant^2 times variance – then if s is noise variance and kernel is K, variance of response is

Filter responses are correlated • Over scales similar to the scale of the filter • Filtered noise is sometimes useful – looks like some natural textures, can be used to simulate fire, etc.

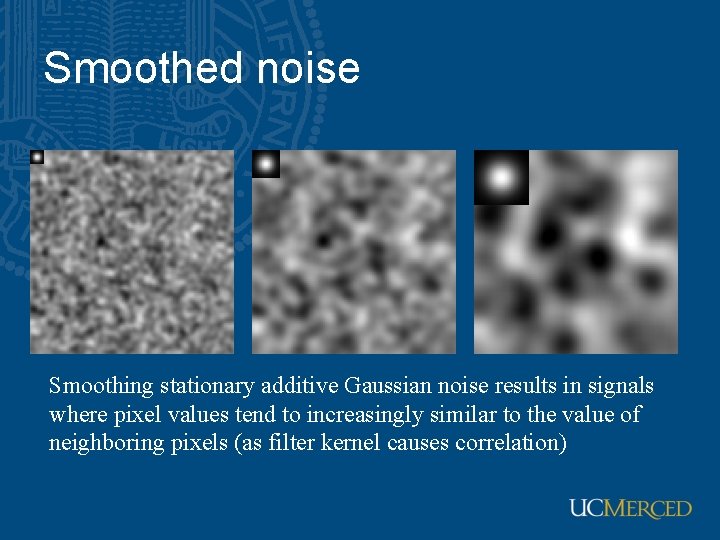
Smoothed noise Smoothing stationary additive Gaussian noise results in signals where pixel values tend to increasingly similar to the value of neighboring pixels (as filter kernel causes correlation)

Smoothing reduces noise • Generally expect pixels to “be like” their neighbours – surfaces turn slowly – relatively few reflectance changes • Generally expect noise processes to be independent from pixel to pixel • Implies that smoothing suppresses noise, for appropriate noise models • Scale – the parameter in the symmetric Gaussian – as this parameter goes up, more pixels are involved in the average – and the image gets more blurred – and noise is more effectively suppressed

The effects of smoothing Each row shows smoothing with gaussians of different width; each column shows different realisations of an image of gaussian noise.

Gradients and edges • Points of sharp change in an image are interesting: – – change in reflectance change in object change in illumination noise • Sometimes called edge points • General strategy – determine image gradient – now mark points where gradient magnitude is particularly large wrt neighbours (ideally, curves of such points). In one dimension, the 2 nd derivative of a signal is zero when the derivative magnitude is extremal a good place to look for edge is where the second derivative is zero.

Smoothing and differentiation • Issue: noise – smooth before differentiation – two convolutions to smooth, then differentiate? – actually, no - we can use a derivative of Gaussian filter • because differentiation is convolution, and convolution is associative

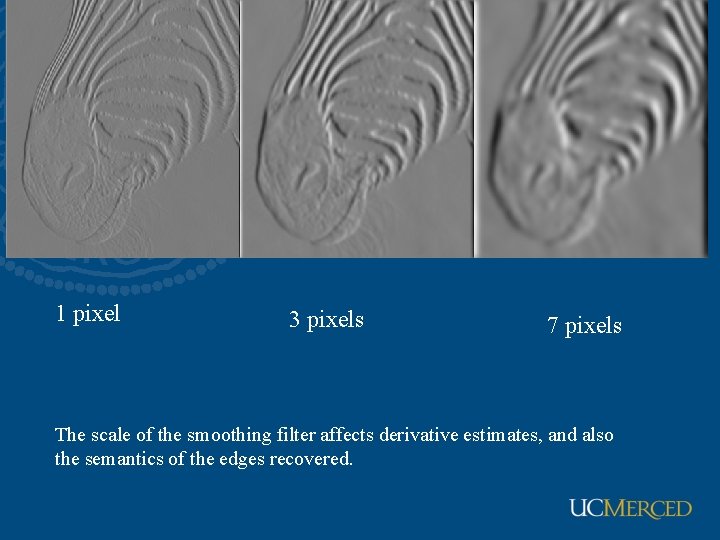
1 pixel 3 pixels 7 pixels The scale of the smoothing filter affects derivative estimates, and also the semantics of the edges recovered.

Image Gradient • Gradient equation: • Represents direction of most rapid change in intensity • Gradient direction: • The edge strength is given by the gradient magnitude

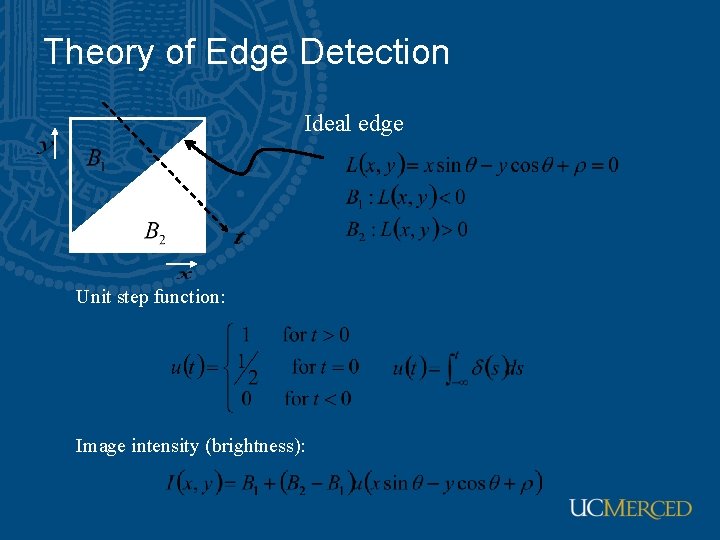
Theory of Edge Detection Ideal edge Unit step function: Image intensity (brightness):

Theory of Edge Detection • Image intensity (brightness): • Partial derivatives (gradients): • Squared gradient: Edge Magnitude: Edge Orientation: (normal of the edge) Rotationally symmetric, non-linear operator

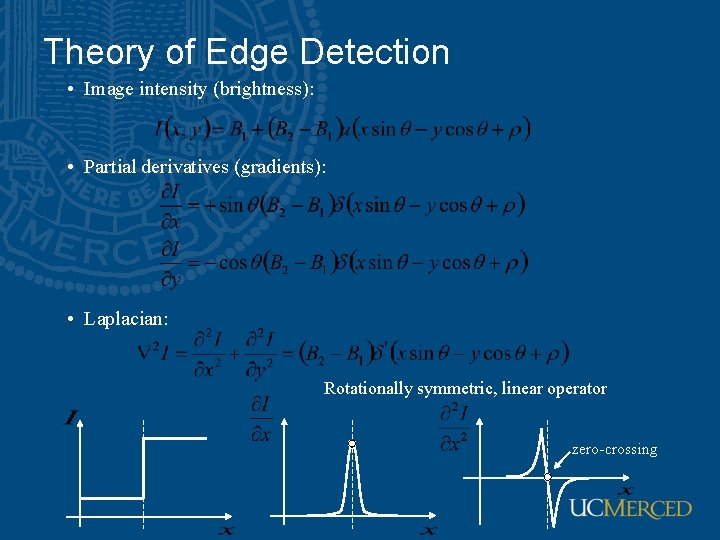
Theory of Edge Detection • Image intensity (brightness): • Partial derivatives (gradients): • Laplacian: Rotationally symmetric, linear operator zero-crossing

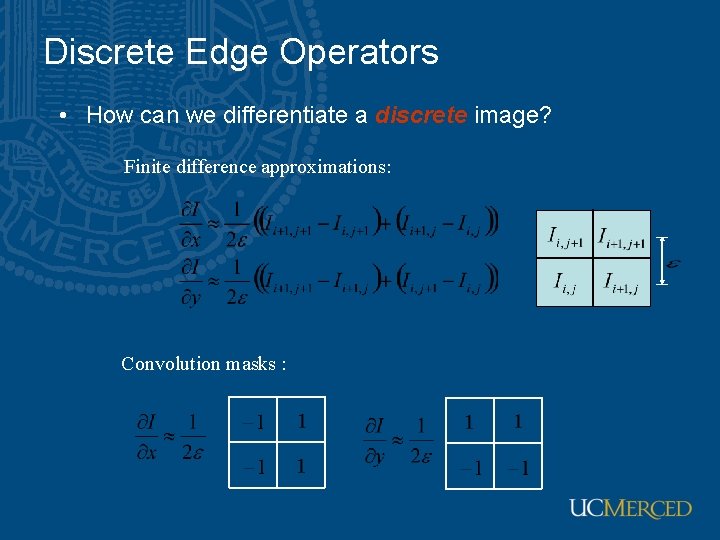
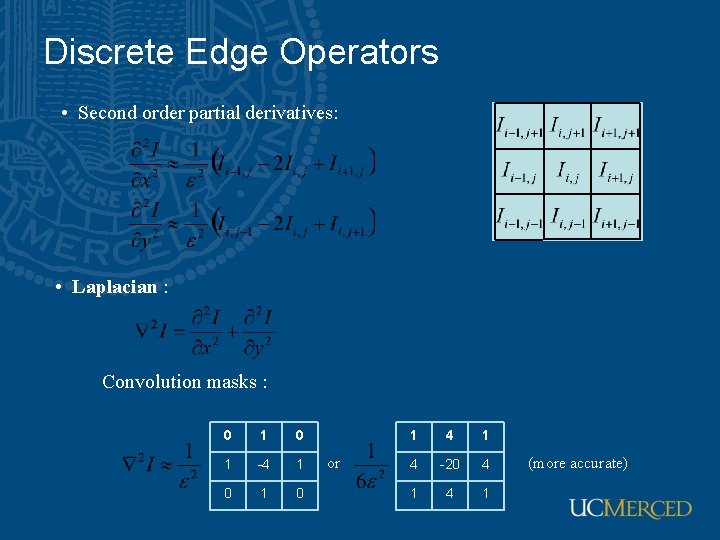
Discrete Edge Operators • How can we differentiate a discrete image? Finite difference approximations: Convolution masks :

Discrete Edge Operators • Second order partial derivatives: • Laplacian : Convolution masks : 0 1 -4 1 0 or 1 4 -20 4 1 (more accurate)

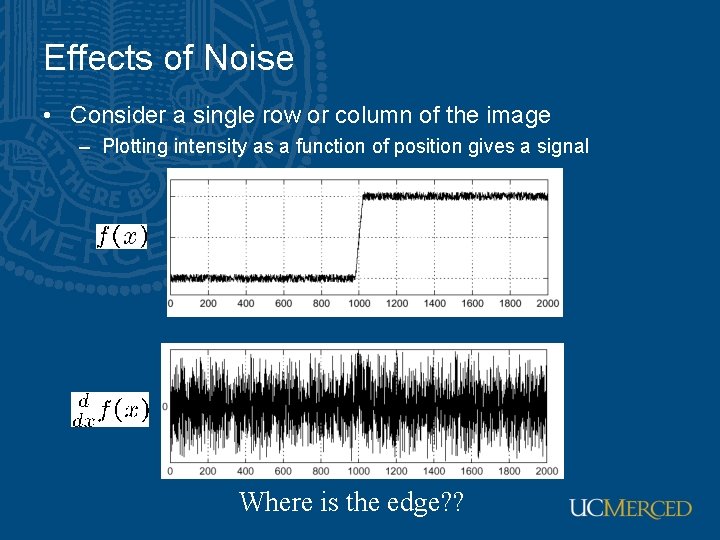
Effects of Noise • Consider a single row or column of the image – Plotting intensity as a function of position gives a signal Where is the edge? ?

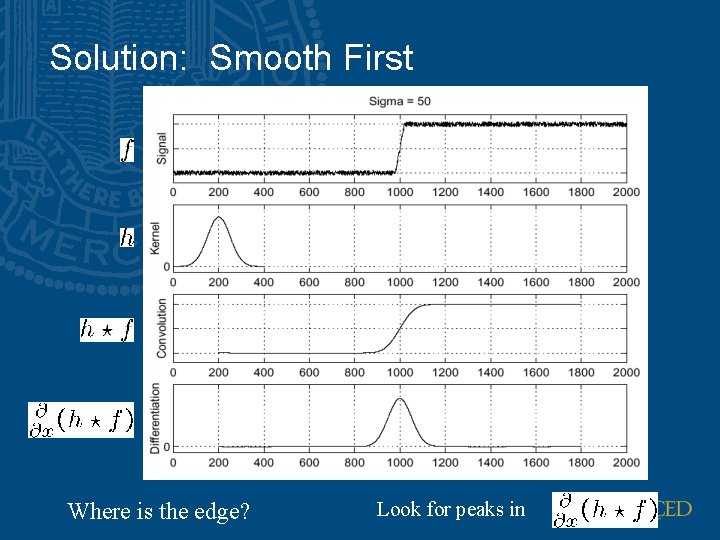
Solution: Smooth First Where is the edge? Look for peaks in

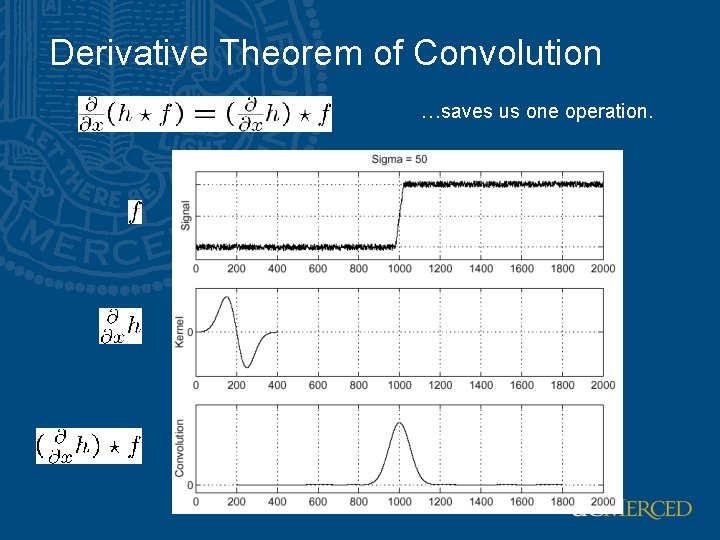
Derivative Theorem of Convolution …saves us one operation.

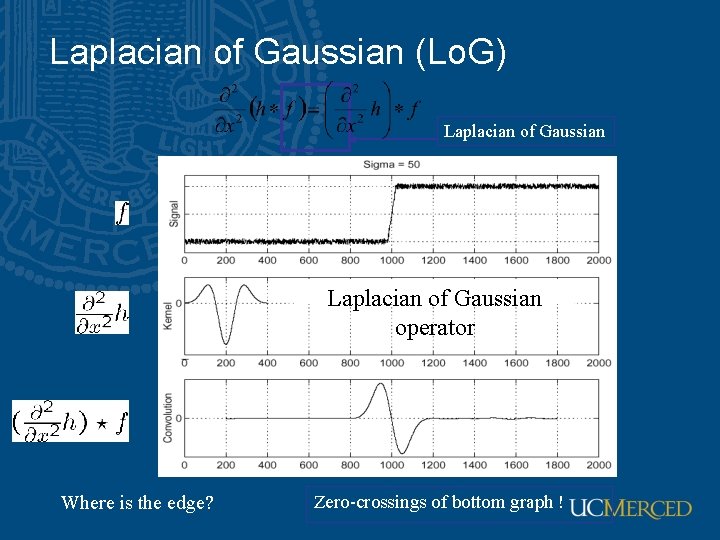
Laplacian of Gaussian (Lo. G) Laplacian of Gaussian operator Where is the edge? Zero-crossings of bottom graph !

2 D Gaussian Edge Operators Gaussian • Derivative of Gaussian (Do. G) Laplacian of Gaussian Mexican Hat (Sombrero) is the Laplacian operator:

threshold sigma=4 scale contrast=1 LOG zero crossings sigma=2 contrast=4

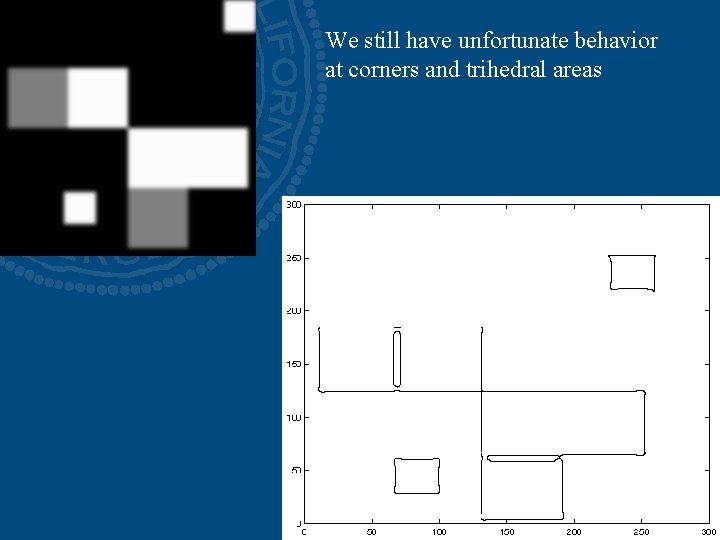
We still have unfortunate behavior at corners and trihedral areas

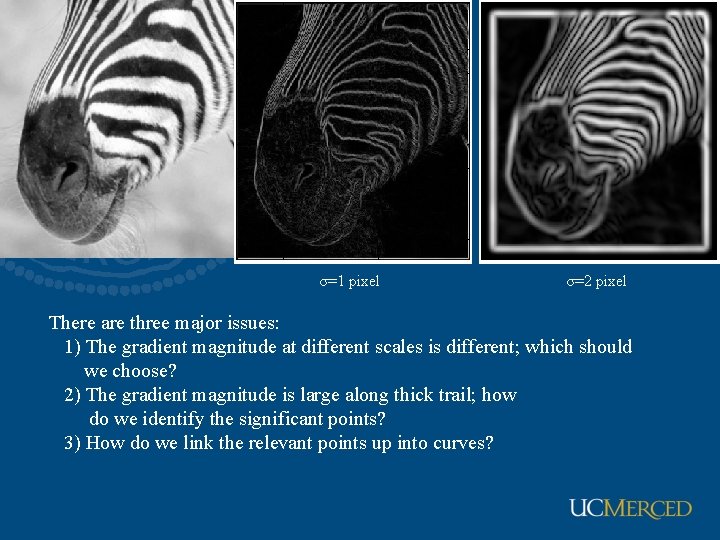
σ=1 pixel σ=2 pixel There are three major issues: 1) The gradient magnitude at different scales is different; which should we choose? 2) The gradient magnitude is large along thick trail; how do we identify the significant points? 3) How do we link the relevant points up into curves?

We wish to mark points along the curve where the magnitude is biggest. We can do this by looking for a maximum along a slice normal to the curve (non-maximum suppression). These points should form a curve. There are then two algorithmic issues: at which point is the maximum, and where is the next one?

Non-maximum Suppression • Check if pixel is local maximum along gradient direction – requires checking interpolated pixels p and r

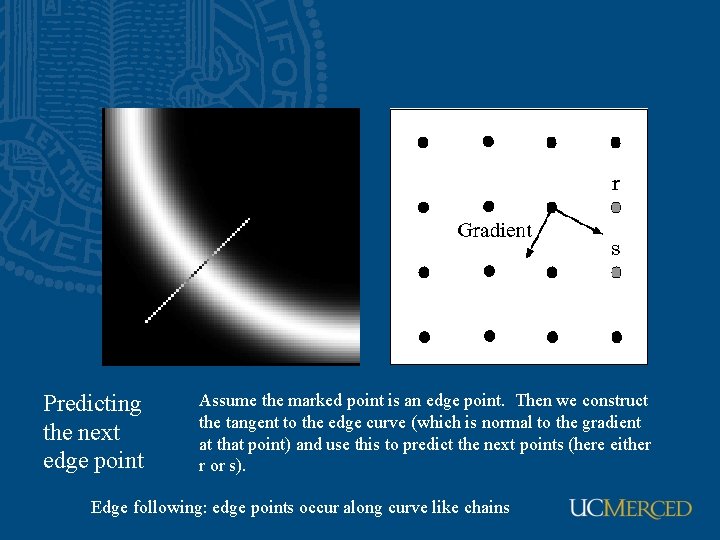
Predicting the next edge point Assume the marked point is an edge point. Then we construct the tangent to the edge curve (which is normal to the gradient at that point) and use this to predict the next points (here either r or s). Edge following: edge points occur along curve like chains

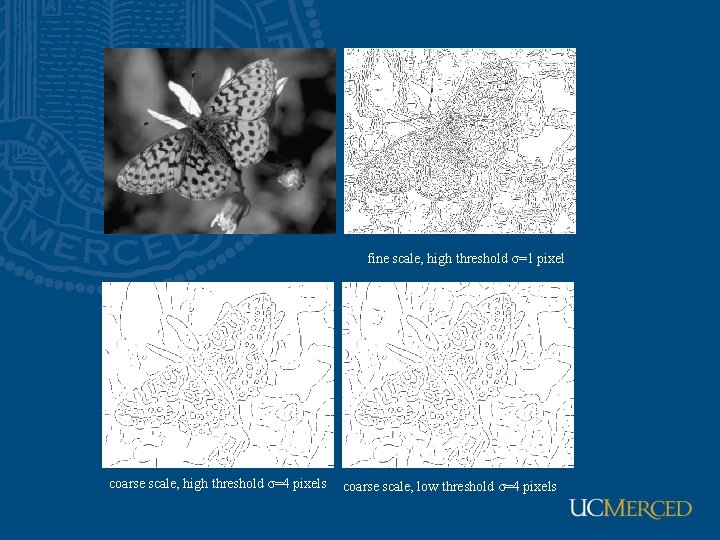
fine scale, high threshold σ=1 pixel coarse scale, high threshold σ=4 pixels coarse scale, low threshold σ=4 pixels

Canny Edge Operator • Smooth image I with 2 D Gaussian: • Find local edge normal directions for each pixel • Compute edge magnitudes • Locate edges by finding zero-crossings along the edge normal directions (non-maximum suppression)

Canny edge detector Original image magnitude of gradient

Canny edge detector After non-maximum suppression

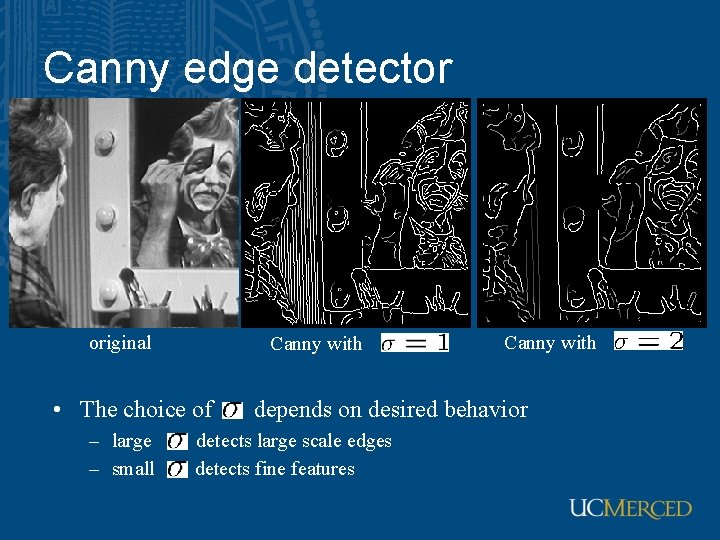
Canny edge detector original Canny with • The choice of – large – small Canny with depends on desired behavior detects large scale edges detects fine features

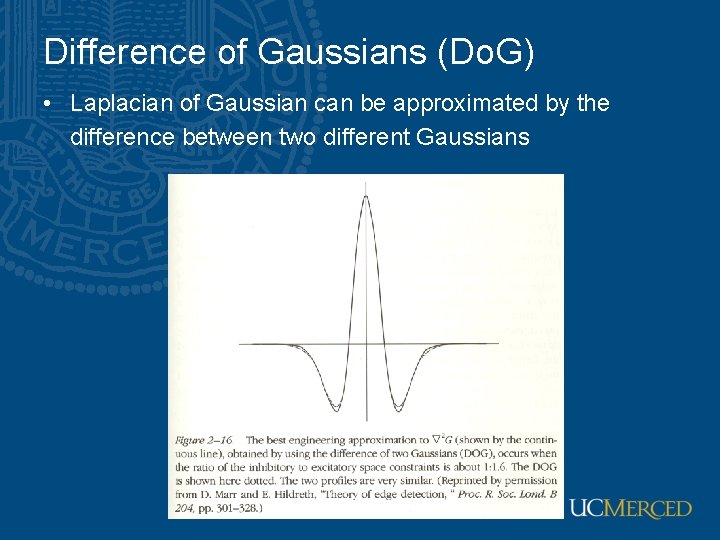
Difference of Gaussians (Do. G) • Laplacian of Gaussian can be approximated by the difference between two different Gaussians

Do. G Edge Detection (a) (b)-(a)

Unsharp Masking – = blurred positive +a increase details in bright area =

Edge Thresholding • Standard Thresholding: • Can only select “strong” edges. • Does not guarantee “continuity”. • Hysteresis based Thresholding (use two thresholds) Example: For “maybe” edges, decide on the edge if neighboring pixel is a strong edge.

Remaining issues • Check that maximum value of gradient value is sufficiently large – drop-outs? use hysteresis • use a high threshold to start edge curves and a low threshold to continue them.

Notice • Something nasty is happening at corners • Scale affects contrast • Edges aren’t bounding contours

Scale space • Framework for multi-scale signal processing • Define image structure in terms of scale with kernel size, σ • Find scale invariant operations • See Scale-theory in computer vision by Tony Lindeberg

Orientation representations • The gradient magnitude is affected by illumination changes – but it’s direction isn’t • We can describe image patches by the swing of the gradient orientation • Important types: – constant window • small gradient mags – edge window • few large gradient mags in one direction – flow window • many large gradient mags in one direction – corner window • large gradient mags that swing

Representing windows Looking at variations • Types – constant • small eigenvalues – edge • one medium, one small – flow • one large, one small – corner • two large eigenvalues

Plotting in ellipses to understand the matrix (variation of gradient) of 3 × 3 window Major and minor axes are along the eigenvectors of H, and the extent corresponds to the size of eigenvalues

Plotting in ellipses to understand the matrix (variation of gradient) of 5 × 5 window

Corners • Harris corner detector • Moravec corner detector • SIFT descriptors

Filters are templates • Applying a filter at some point can be seen as taking a dotproduct between the image and some vector • Filtering the image is a set of dot products convolution is equivalent to taking the dot product of the filter with an image patch • Insight – filters look like the effects they are intended to find – filters find effects they look like derivative of Gaussian used as edge detection

Normalized correlation • Think of filters of a dot product – now measure the angle – i. e normalised correlation output is filter output, divided by root sum of squares of values over which filter lies – cheap and efficient method for finding patterns • Tricks: – ensure that filter has a zero response to a constant region (helps reduce response to irrelevant background) – subtract image average when computing the normalizing constant (i. e. subtract the image mean in the neighbourhood) – absolute value deals with contrast reversal

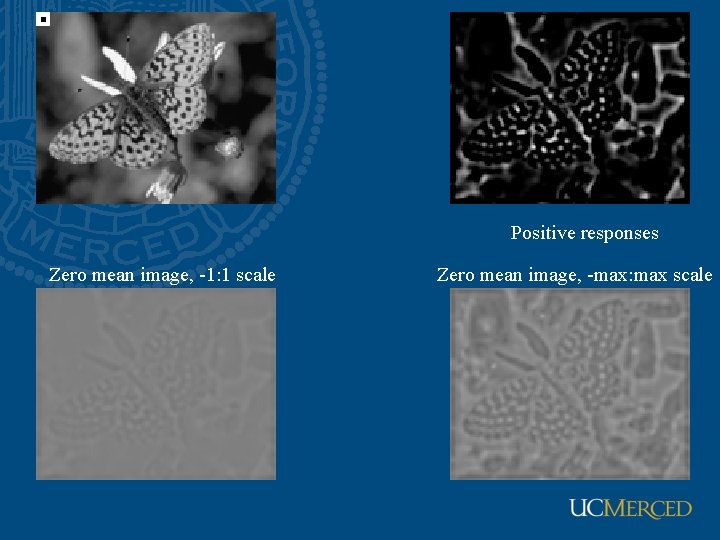
Positive responses Zero mean image, -1: 1 scale Zero mean image, -max: max scale

Positive responses Zero mean image, -1: 1 scale Zero mean image, -max: max scale

Figure from “Computer Vision for Interactive Computer Graphics, ” W. Freeman et al, IEEE Computer Graphics and Applications, 1998 copyright 1998, IEEE

Anistropic scaling • Symmetric Gaussian smoothing tends ot blur out edges rather aggressively • Prefer an oriented smoothing operator that smoothes – aggressively perpendicular to the gradient – little along the gradient • Also known as edge preserving smoothing • Formulated with diffusion equation

Diffusion equation for anistropic filter • PDE that describes fluctuations in a material undergoing diffusion • For istropic filter • For anistropic filter

Anistropic filtering

Edge preserving filter • Bilateral filter – Replace pixel’s value by a weighted average of its neighbors in both space and intensity One iteration Multiple iterations