Singular Value Decomposition SVD T11 Computer Vision University

Singular Value Decomposition (SVD) T-11 Computer Vision University of Ioannina Christophoros Nikou

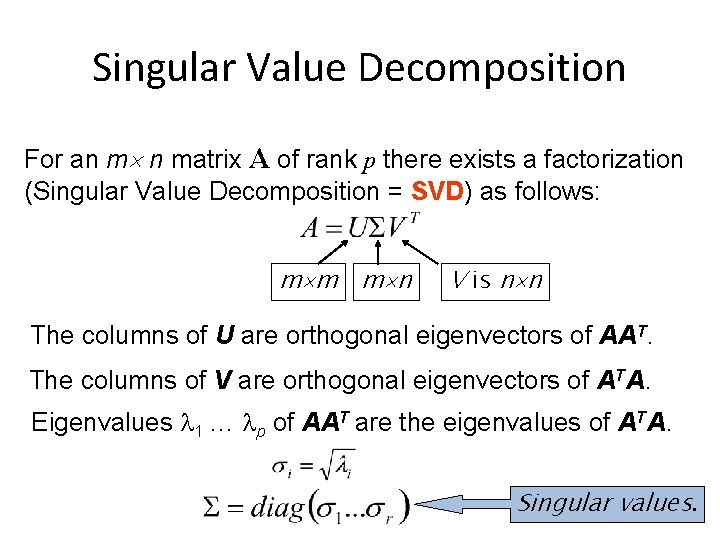
Singular Value Decomposition For an m n matrix A of rank p there exists a factorization (Singular Value Decomposition = SVD) as follows: m m m n V is n n The columns of U are orthogonal eigenvectors of AAT. The columns of V are orthogonal eigenvectors of ATA. Eigenvalues 1 … p of AAT are the eigenvalues of ATA. Singular values.

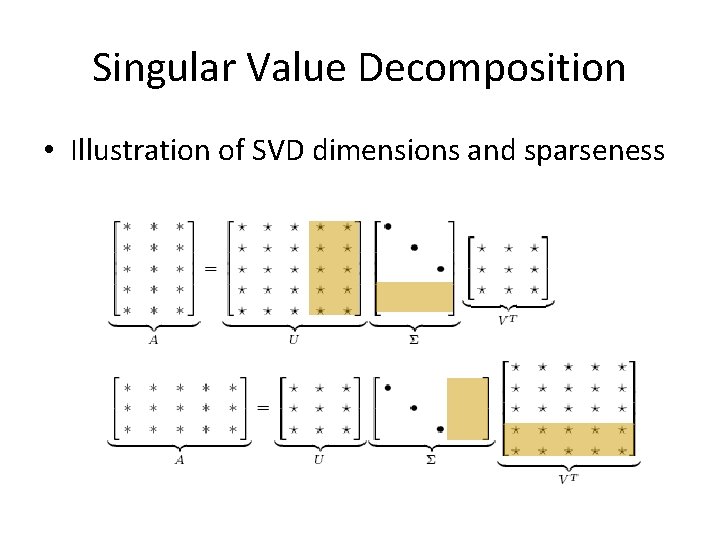
Singular Value Decomposition • Illustration of SVD dimensions and sparseness

SVD example Let Thus m=3, n=2. Its SVD is Typically, the singular values arranged in decreasing order.

Proof by construction Let m>n and rank(A)=p<n without loss of generality. Compute the eigenvalues of the positive semi-definite matrix ATA and name their square roots singular values:

Proof by construction

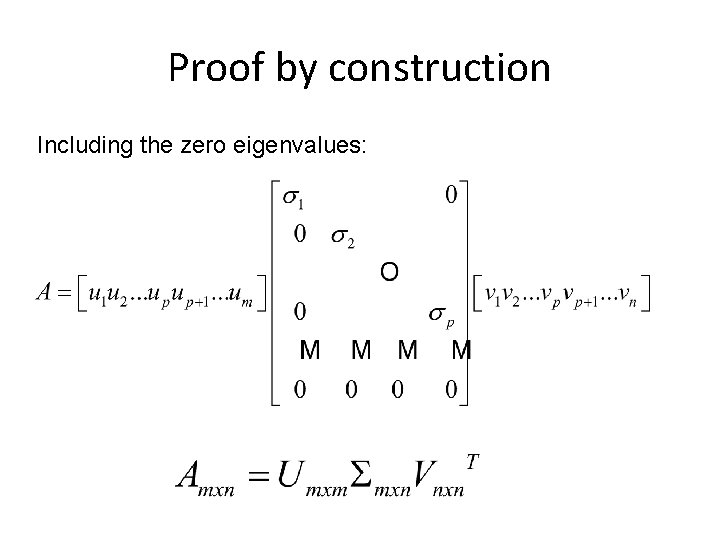
Proof by construction Including the zero eigenvalues:

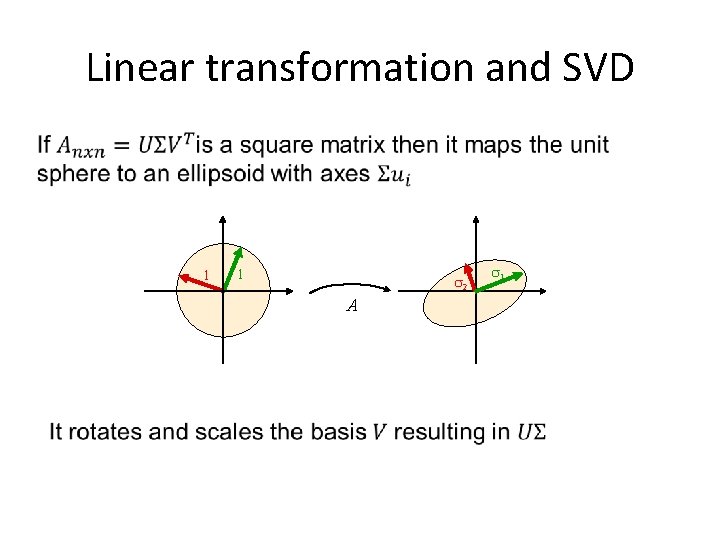
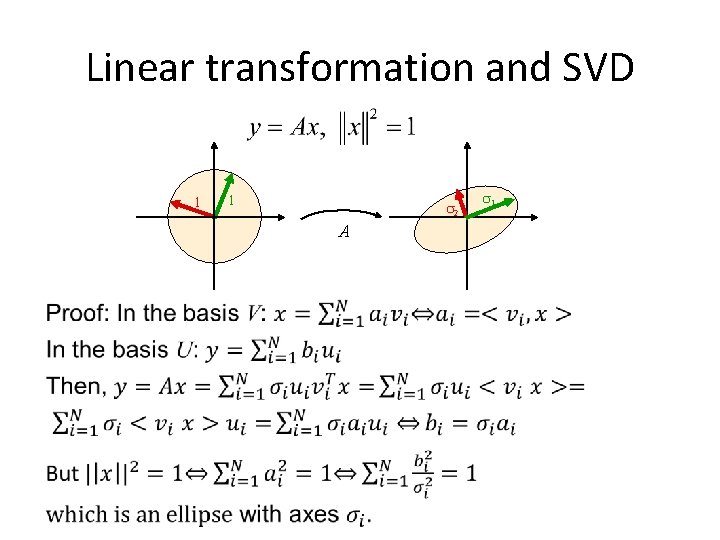
Linear transformation and SVD 1 1 2 A 1

Linear transformation and SVD 1 1 2 A 1

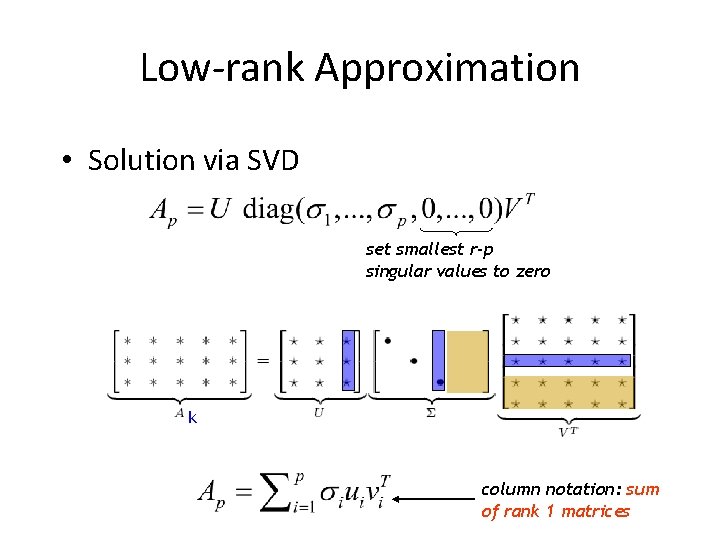
Low-rank Approximation • Given matrix A with rank(A)=r, estimate matrix X, with rank(X)=p<r, such that:

Low-rank Approximation • Solution via SVD set smallest r-p singular values to zero k column notation: sum of rank 1 matrices

Approximation error • How good (bad) is this approximation? • It’s the best possible, measured by the Frobenius norm of the error: • Frobenius error drops as p increases.

Approximation error First approximation to A is second approximation to A is

Application to image compression G. Strang, Linear Algebra and its Applications p 444 It is better to find the essential information in the 1000 by 1000 matrix, and send only that. Suppose we know the SVD. The key is in the singular values. Typically, some are significant and others are extremely small. If we keep 60 and throw away 940, then we send only the corresponding 60 columns of U, and V. The other 940 columns are multiplied by small singular values that are being ignored. In fact, we can do the matrix multiplication as columns times rows: If only 60 terms are kept, we send 60 times 2000 numbers instead of a million.

Application to image compression the SVD of a 32 -times-32 digital image A is computed

Application to image compression G. Strang: “ At first you see nothing, and suddenly you recognize everything. ”

Moore-Penrose pseudoinverse Simply invert the non zero singular values of A. Useful for solving over-constrained linear systems:

Solution using SVD

Solution using Lagrange multipliers

Solution using SVD Set a constraint to avoid the trivial solution

Orthogonal Procrustes problem

Orthogonal Procrustes problem

Historical notes Trefethen (Textbook author): q. The SVD was discovered independently by Beltrami(1873) and Jordan(1874) and again by Sylvester(1889). q. The SVD did not become widely known in applied mathematics until the late 1960 s, when Golub and others showed that it could be computed effectively. Cleve Moler (invented MATLAB, co-founded Math. Works) Gene Golub has done more than anyone to make the singular value decomposition one of the most powerful and widely used tools in modern matrix computation. In later years he drove a car with the license plate: