EECS 274 Computer Vision Projective Structure from Motion

EECS 274 Computer Vision Projective Structure from Motion

Projective structure from motion • The Projective Structure from Motion Problem • Elements of Projective Geometry • Projective Structure and Motion from Two Images • Projective Motion from Fundamental Matrices • Projective Structure and Motion from Multiple Images • From Projective to Euclidean Images • Reading: FP Chapter 8

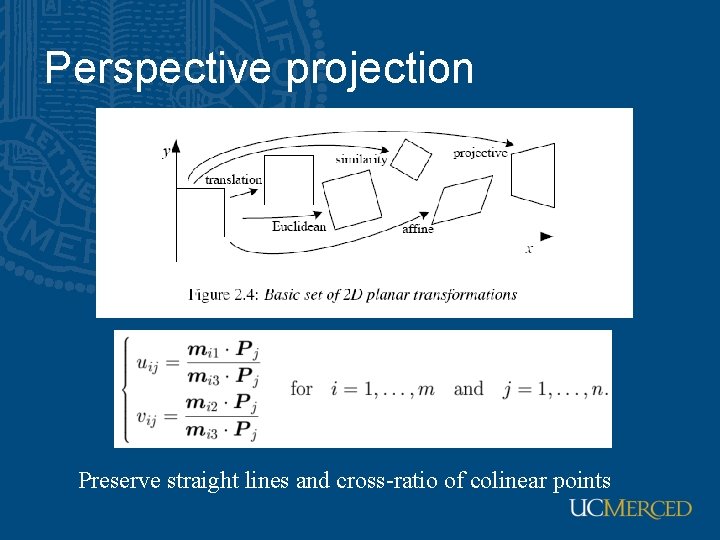
Perspective projection Preserve straight lines and cross-ratio of colinear points

Perspective projection • Recall

The projective structure-from-motion problem Given m perspective images of n fixed points P we can write j Problem: estimate the m 3× 4 matrices M iand the n positions P j from the mn correspondences p. ij 2 mn equations in 11 m+3 n unknowns Overconstrained problem, that can be solved using (non-linear) least squares!

The projective ambiguity of projective SFM When the intrinsic and extrinsic parameters are unknown If M i and P are solutions, j So are M’ and P’ where i j and Q is an arbitrary non-singular 4× 4 matrix. Q is a projective transformation.

Projective ambiguity • Take ambiguity into account, the problem admits a finite number of solution as 2 mn ≥ 11 m+3 n-15 • For two-view (m=2), 7 point correspondences are sufficient to solve projective structure from motion

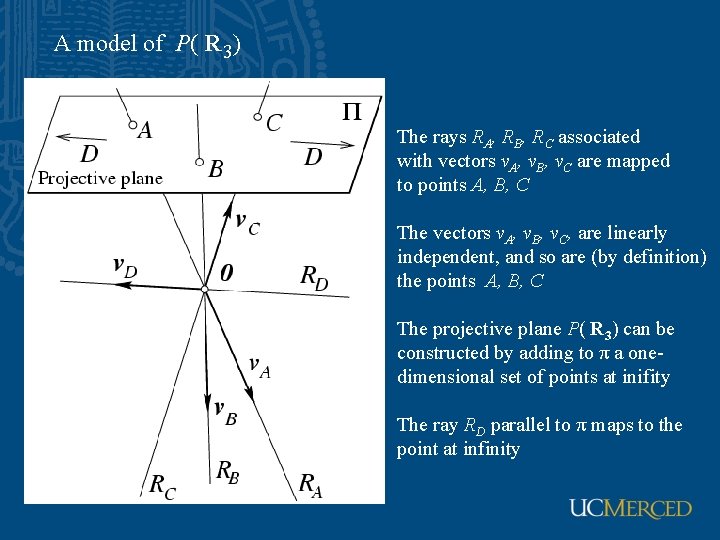
Projective spaces: (semi-formal) definition

A model of P( R 3) The rays RA, RB, RC associated with vectors v. A, v. B, v. C are mapped to points A, B, C The vectors v. A, v. B, v. C, are linearly independent, and so are (by definition) the points A, B, C The projective plane P( R 3) can be constructed by adding to π a onedimensional set of points at inifity The ray RD parallel to π maps to the point at infinity

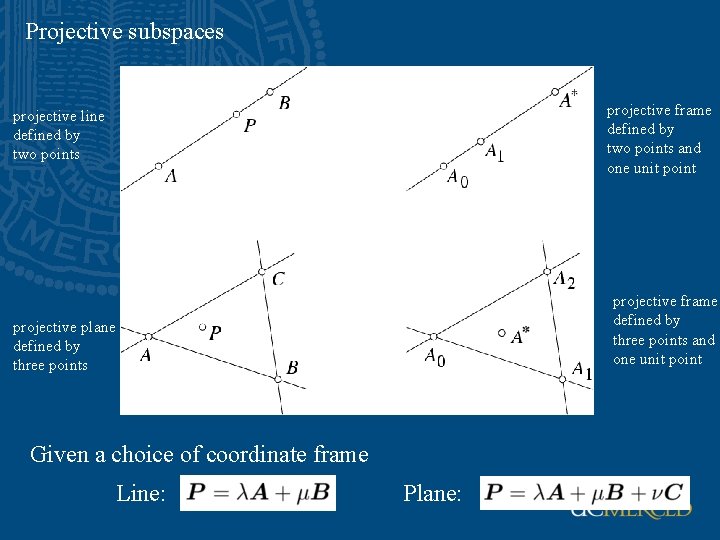
Projective subspaces and projective coordinates

Projective coordinates defined in terms of points m+1 linearly independent points P A* is linear dependent on Ai Projective coordinates

Projective coordinates • Determined by the m+1 fundamental points Ai and the unit point A* • Coordinate vectors in the projective frame have a simple form

Projective subspaces projective frame defined by two points and one unit point projective line defined by two points projective frame defined by three points and one unit point projective plane defined by three points Given a choice of coordinate frame Line: Plane:

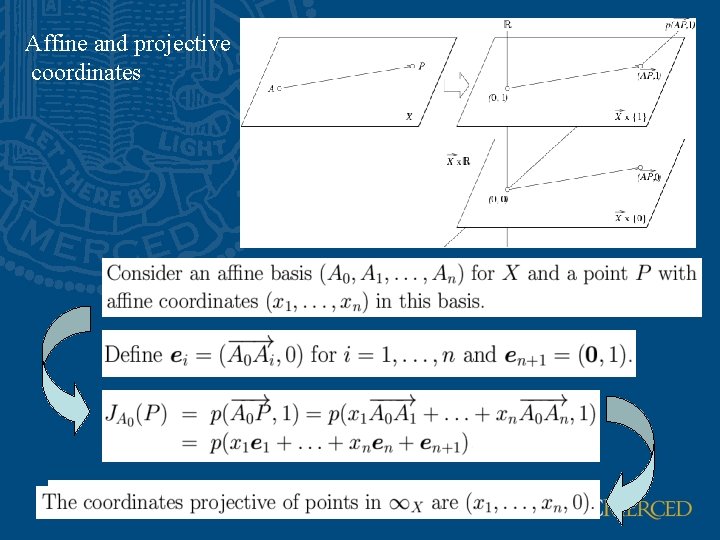
Affine and projective spaces

Affine and projective coordinates

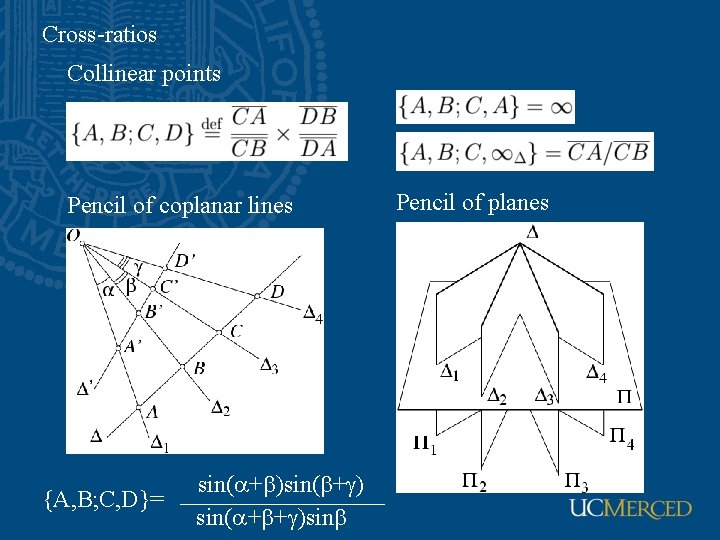
Cross-ratios Collinear points Pencil of coplanar lines {A, B; C, D}= sin( + ) sin( + + )sin Pencil of planes

Cross-ratios and projective coordinates Along a line equipped with the basis In a plane equipped with the basis In 3 -space equipped with the basis *

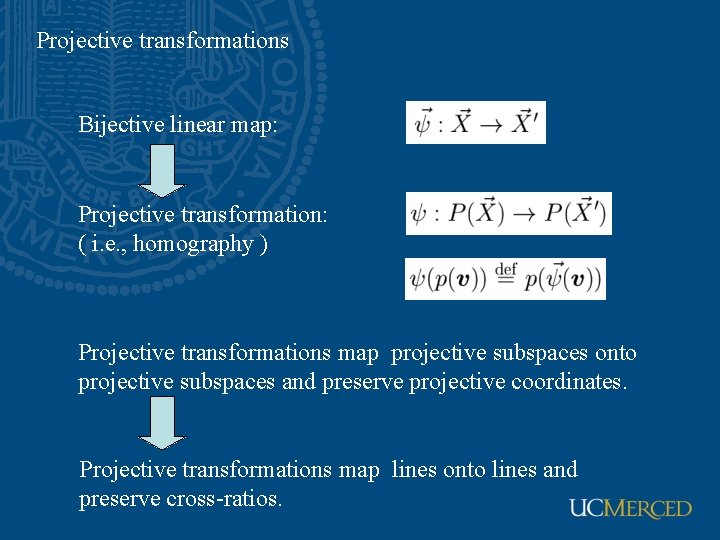
Projective transformations Bijective linear map: Projective transformation: ( i. e. , homography ) Projective transformations map projective subspaces onto projective subspaces and preserve projective coordinates. Projective transformations map lines onto lines and preserve cross-ratios.

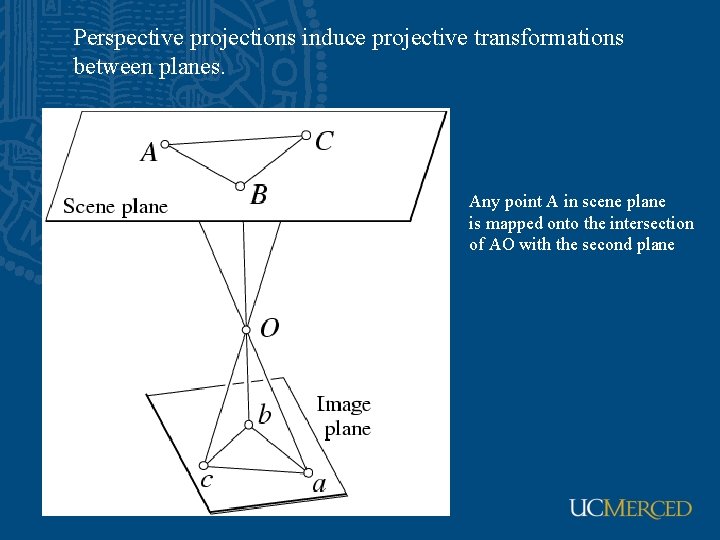
Perspective projections induce projective transformations between planes. Any point A in scene plane is mapped onto the intersection of AO with the second plane

Reference

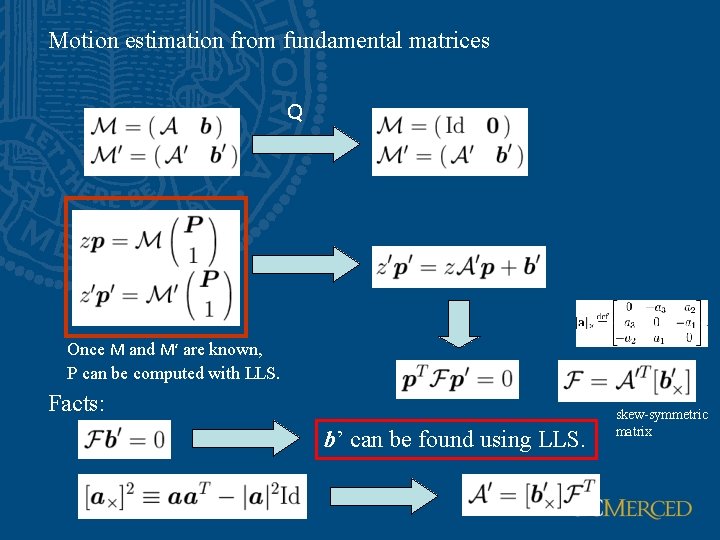
Motion estimation from fundamental matrices Q Once M and M’ are known, P can be computed with LLS. Facts: b’ can be found using LLS. skew-symmetric matrix

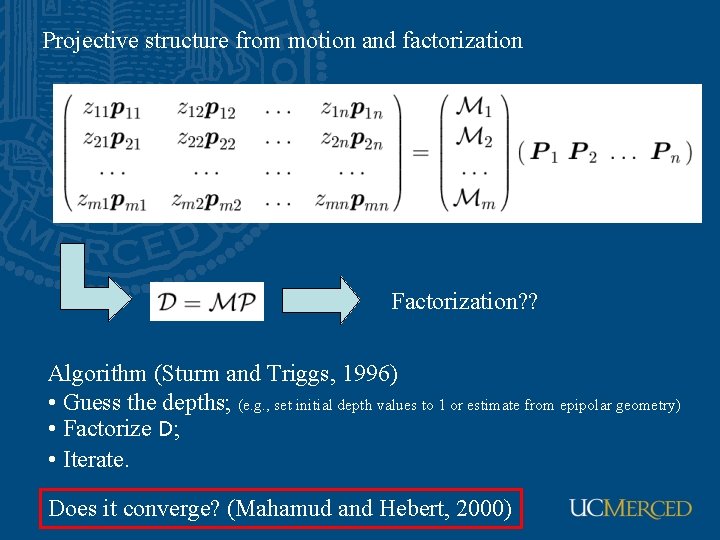
Projective structure from motion and factorization Factorization? ? Algorithm (Sturm and Triggs, 1996) • Guess the depths; (e. g. , set initial depth values to 1 or estimate from epipolar geometry) • Factorize D; • Iterate. Does it converge? (Mahamud and Hebert, 2000)

Bundle adjustment (photogrammetry) Minimize with respect to the matrices Mi and the point positions Pj. • Nonlinear least squares minimization • Expensive but offers the advantage of combining all measurements to minimize error measure • Mean square error between the actual image point position and those predicted using the estimated scene structure and camera motion See “Bundle Adjustment —A Modern Synthesis” by Triggs et al.

From projective to Euclidean images If z , P , R and t are solutions, so are l z , l P , R and l t. Absolute scale cannot be recovered! The Euclidean shape (defined up to an arbitrary similitude) is the best that can be recovered.

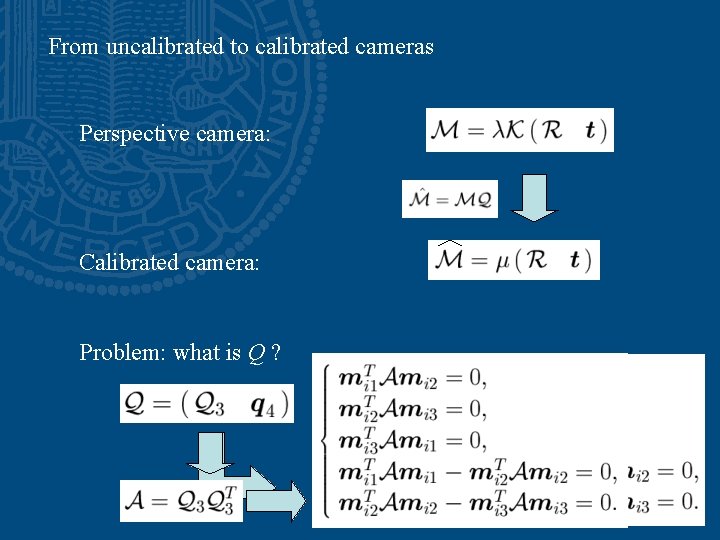
From uncalibrated to calibrated cameras Perspective camera: Calibrated camera: Problem: what is Q ?

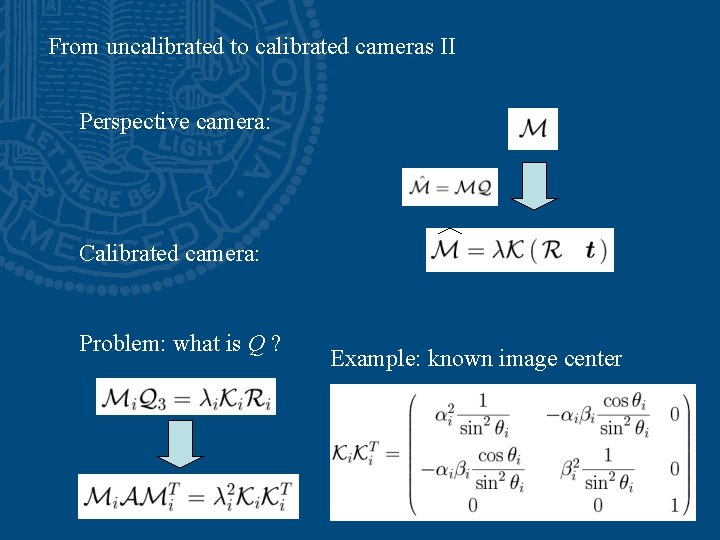
From uncalibrated to calibrated cameras II Perspective camera: Calibrated camera: Problem: what is Q ? Example: known image center

(Pollefeys, Koch and Van Gool, 1999) Reprinted from “Self-Calibration and Metric 3 D Reconstruction from Uncalibrated Image Sequences, ” by M. Pollefeys, Ph. D Thesis, Katholieke Universiteit, Leuven (1999).