Mathematical Foundations of Computer Graphics Computer Vision and

Mathematical Foundations of Computer Graphics, Computer Vision and Computation in Projective Space Vaclav Skala skala@kiv. zcu. cz subj. AMDO 2006 Center of Computer Graphics and Visualization http: //herakles. zcu. cz Department of Computer Science and Engineering http: //www. kiv. zcu. cz Faculty of Applied Sciences http: //www. fav. zcu. cz University of West Bohemia http: //www. zcu. cz Plzen, Czech Republic AMDO 2006 No. slides 53

Contents • • • Vectors and Points in Geometry Vectors and Matrices Lines and Line Segments Principle of Duality Computation in Projective Space Barycentric Coordinates Length, Area and Volume Intersection Computation in Projective Space Cg / HLSL and GPU Computing Conclusion References AMDO 2006 No. slides 53 3

Vectors and Points in Geometry • A vector v has a magnitude (length) and direction. • Normalized vectors have magnitude 1, e. g. ║v║=1 • Zero vector 0 has magnitude zero, no direction • Vectors do not have a location!! • Vectors and points have only a similar representation !! AMDO 2006 No. slides 53 4

Vectors and Points in Geometry Algebraic rules - properties • v+w=w+v commutative • u+(v+w)=(u+v)+w associative • u+0=u additive identity • For every v there is a vector –v such that v+(-v)=0 • (ab)v=a(bv) associative • (a+b)v=av+bv distributive • a(v+w)=av+bw distributive • 1. v=v multiplicative identity AMDO 2006 No. slides 53 v u w v+w u+v+w scalar multiplication 5

Vectors and Points in Geometry Vector representation in R 2 x 0+x 1 = (x 0, y 0)+(x 1, y 1) = (x 0+x 1, y 0+y 1) a x 0 = a(x 0, y 0) = (ax 0, ay 0) Direct generalization to R 3 and Rn Linear combination v = a 0 v 0+ a 1 v 1+…. . + an-1 vn-1 If vi = a 0 v 0+ a 1 v 1+. . ai-1 vi-1+ ai+1 vi+1+. . . + an-1 vn-1 then vi is linearly dependent – two linearly dependent vectors v and w are said to be parallel, e. g. w = av AMDO 2006 No. slides 53 6

Vectors and Points in Geometry Standard vector basis for R 3 e 0 = (1, 0, 0), e 1 = (0, 1, 0), e 2 = (0, 0, 1) usually as {i, j, k} , where i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1) coefficients a 0, a 1, a 2, commonly represented as x, y, z R 3 Vector v in v = xi + yj+zk AMDO 2006 k v z y x j i No. slides 53 7

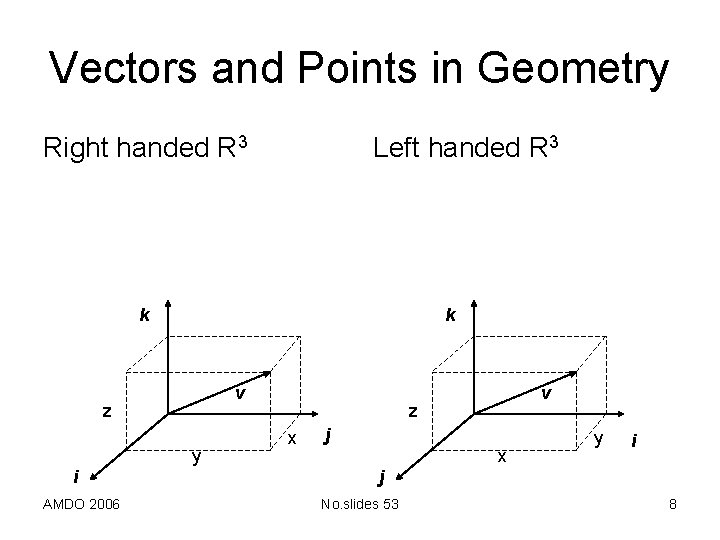
Vectors and Points in Geometry Right handed R 3 Left handed R 3 k k v z y i AMDO 2006 v z x j x y i j No. slides 53 8

Vectors and Points in Geometry Vector length and norm ║v║≥ 0 ║v║=0 v = 0 ║a v║= │a│║v║ ║v + w║≤ ║v ║+ ║w║ ║v║= (∑ vi 2 )1/2 Euclidean norm usually Pythagorean theorem x 2 + y 2 = d 2 in R 3 AMDO 2006 x 2 + y 2 + z 2 = ║v║ 2 No. slides 53 9

Vectors and Points in Geometry Inner product ‹v , w› = ‹w , v› - symmetry ‹u+v , w› = ‹u , w› + ‹v , w› - additivity a ‹v , w› = ‹a v , w› = ‹v , a w› - homogeneity ‹v , v› ≥ 0 - positivity w ‹v , v› = 0 v = 0 - definiteness Euclidean inner product – dot product ‹v , w›= v. w = ║v║║w║cos AMDO 2006 No. slides 53 v 10

Vectors and Points in Geometry Cross (vector) product v x w = -(w x v ) – it is not commutative !! u x (v + w) = u x v + u x w (u + v) x w = u x w + v x w a (u x v) = (a u) x v = u x (av) ux 0=0 xu=0 vxv=0 vxw w v ║v x w ║ = ║v║║w║sin The length of the v x w equals to area of parallelogram AMDO 2006 No. slides 53 11

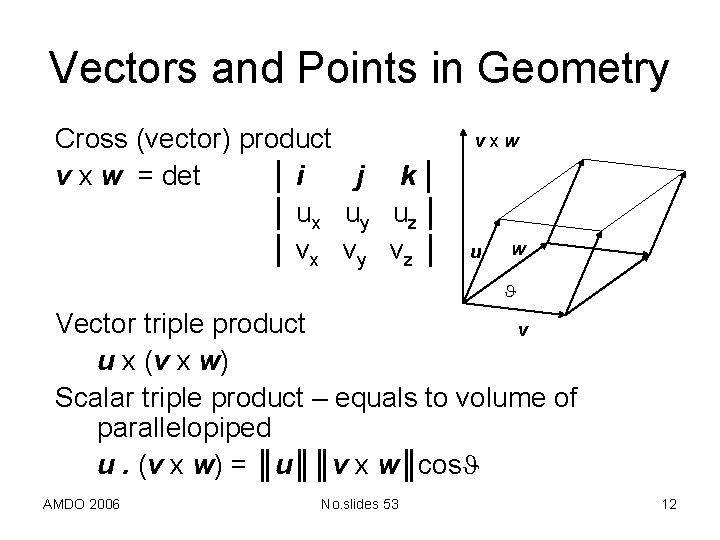
Vectors and Points in Geometry Cross (vector) product v x w = det │i j k│ │ ux uy uz │ │ vx vy vz │ vxw u w Vector triple product v u x (v x w) Scalar triple product – equals to volume of parallelopiped u. (v x w) = ║u║║v x w║cos AMDO 2006 No. slides 53 12

Vectors and points in geometry Algebraic rules: Vector triple product u x (v x w) = (u. w)v - (u. v)w (u x v) x w = (u. w)v - (v. w)u u. (v x w) = w. (u x v) = v. (w x u) Outer (tensor) product – result is a MATRIX Q Q = u. Tv qij = ui vj - will be defined latter Tip: CPU and GPU optimized for vector/parallel comp. AMDO 2006 No. slides 53 13

Vectors and Points in Geometry Vectors – movable, no fixed position Points – no size, position fixed in the GIVEN coordinate system k Coordinate systems: • Cartesian – right handed v system is used z • Polar y i • Spherical • and many others AMDO 2006 No. slides 53 x j 14

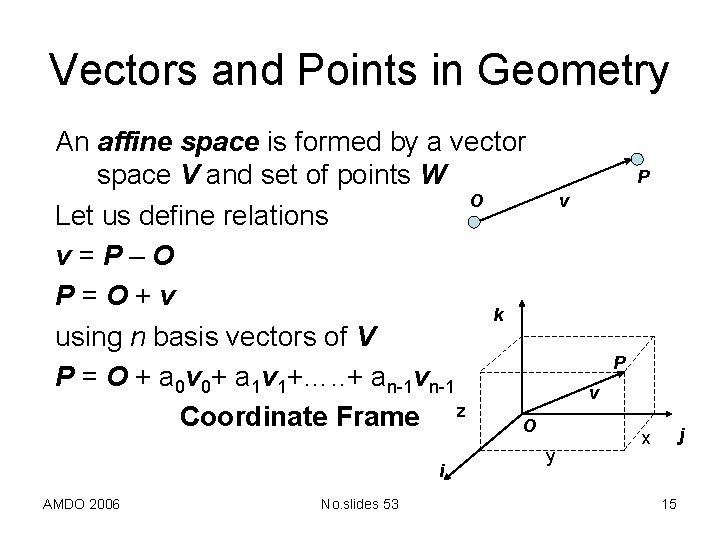
Vectors and Points in Geometry An affine space is formed by a vector space V and set of points W O Let us define relations v=P–O P=O+v k using n basis vectors of V P = O + a 0 v 0+ a 1 v 1+…. . + an-1 vn-1 Coordinate Frame z O i AMDO 2006 No. slides 53 P v y j x 15

Vectors and Points in Geometry An affine combinations P = a 0 P 0+ a 1 P 1+…. . + ak-1 Pk-1 and a 0+ a 1+…. . + ak-1=1 or a 0 = 1 - a 1 -…. . - ak-1 Convex combination 0 ≤ a 0+ a 1+…. . + ak-1 ≤ 1 P = P 0+ a 1 (P 1 - P 0) …. . + ak-1 (Pk-1 - P 0) if vi = P 1 - P 0 then P = P 0+ a 1 v 1 …. . + ak-1 vk-1 AMDO 2006 No. slides 53 16

Vectors and Points in Geometry Vector representation v = ( vx , vy , vz , 0 ) Point representation P = ( Px , Py , Pz , 1 ) Many libraries do not distinguish between points and vector and treat them in the same manner !! – BE CAREFUL ! v = P 1 – P 0 = ( Px 1 , Py 1 , Pz 1 , 1 ) - ( Px 0 , Py 0 , Pz 0 , 1 ) = ( Px 1 – Px 0 , Py 1 – Py 0 , Pz 1 – Pz 0 , 0 ) = ( vx , vy , vz , 0 ) AMDO 2006 No. slides 53 17

Vectors and Matrices Vector – any vector in n-dimensional vector space V can be represented as x = x 0 v 0 + x 1 v 1 + …. . + xn-1 vn-1 + where {v 0 , v 1 , …, vn-1 } is a basis vector of V AMDO 2006 No. slides 53 18

Vectors and Matrices Matrix – square matrix n = m A = [aij] Special cases m = 1 - column matrix – vector (used in the right handed coordinate system) n = 1 - row matrix - vector AMDO 2006 No. slides 53 19

Vectors and Matrices Algebraic rules A+B=B+A A + (B + C) = (A + B) + C A+0=A A + (-A) = 0 a(A + B) = a. A + Ab (a+b)A = a. A + b. A 1. A = A AMDO 2006 Transpose of a matrix A is a matrix B = AT where: bij = aij Additional rules (AT)T = A (a. AT)T = a. AT (A+B)T = AT + BT No. slides 53 20

Vectors and Matrices Matrix multiplication C=AB A = [aik ] B = [bkj ] C = [cij ] i = 1, …, n, k = 1, …, p, j = 1, …, m i = 1, …, n, j = 1, …, m NOTE! AB≠BA AMDO 2006 No. slides 53 21

Vectors and Matrices Block matrices A(BC)=(AB)C A(B + C)=AB+ AC (AB)T=BT+AT AMDO 2006 a(BC)=(a. B)C (A + B)+ C = AC+ BC No. slides 53 22

Lines and Line Segments Lines in E 2 • implicit description • parametric description • two points define a line p x 1 p x 0 AMDO 2006 No. slides 53 23

Lines and Line Segments Lines in E 2 • two points define a line p • we have 2 equations for 3 parameters – a, b, d • we have to solve linear homogeneous system, i. e. one parametric solution AMDO 2006 No. slides 53 x 1 p x 0 24

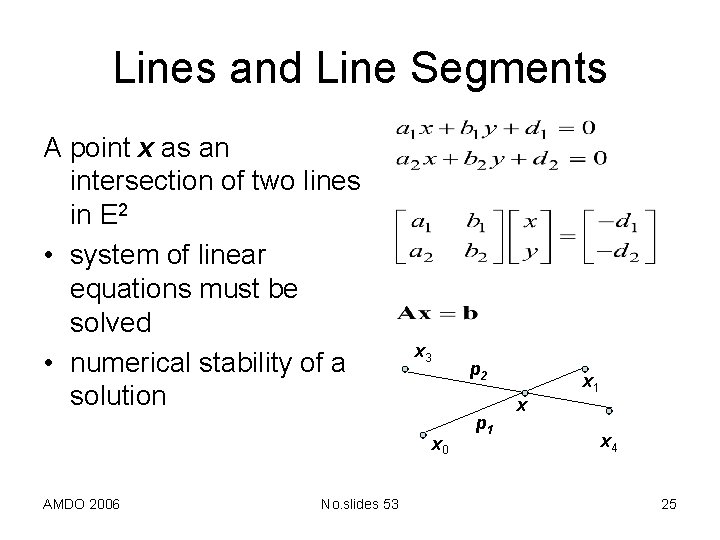
Lines and Line Segments A point x as an intersection of two lines in E 2 • system of linear equations must be solved • numerical stability of a solution x 3 p 2 x 0 AMDO 2006 No. slides 53 p 1 x x 4 25

Principle of Duality Any theorems remain true in E 2 when we interchange words “point” and “line”, “lie on” and “pass through”, “join” and “intersection” etc. Points and planes are dual in E 3 etc. (not points and lines!) It means that intersection of two lines and a line given by two points should be same if we use the principle of duality. AMDO 2006 No. slides 53 26

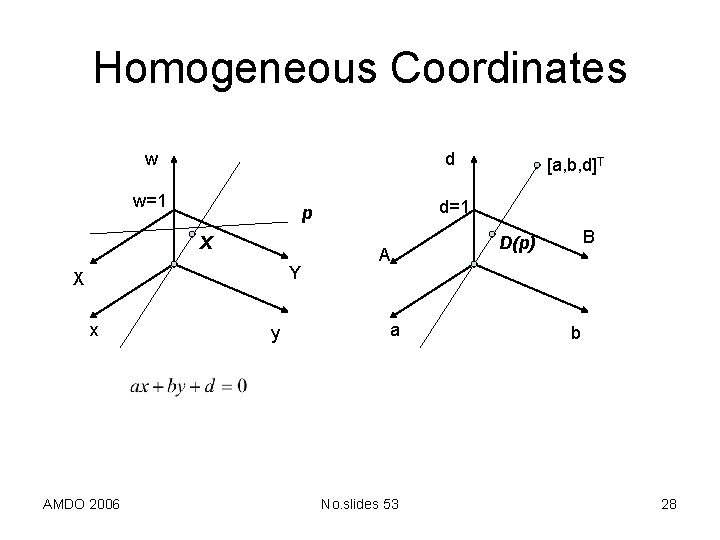
Homogeneous Coordinates • Projective extension of Affine space • A point x is defined in E 2 with coordinates X = (X, Y) or as a point x = [x, y, w]T, where w = 1 usually • It is a line (without an origin) in the projective space P 2 • A point x is defined in E 3 with coordinates X = (X, Y, Z) or as a point x = [x, y, z, w]T, where w = 1 usually • It is a line (without an origin) in the projective space P 3 AMDO 2006 No. slides 53 27

Homogeneous Coordinates w d w=1 Y X x AMDO 2006 d=1 p X y [a, b, d]T A a No. slides 53 B D(p) b 28

Computation in Projective Space An intersection point x given by two lines p 1=[a 1, b 1, d 1]T and p 2=[a 2, b 2, d 2]T x = p 1 x p 2 AMDO 2006 No. slides 53 29

Computation in Projective Space Lines in E 2 • a line p is defined by points x 1=[x 1, y 1, w 1]T x 2=[x 2, y 2, w 2]T x 2 p x 1 p = x 1 x x 2 • we have do not need to solve linear equations and no division operation is needed! AMDO 2006 No. slides 53 30

Computation in Projective Space AMDO 2006 No. slides 53 31

Computation in Projective Space • A line can be determined using by cross product of two points • An intersection point can be determined by cross product of two lines How E 3 case is handled? • A point is dual to a plane ρ ρ=[a, b, c, d]T • There is no “direct duality” for a line in E 3 AMDO 2006 No. slides 53 32

Computation in Projective Space • Cross product definition • A plane ρ is determined as a cross product of three given points Due to duality • An intersection point x of three planes is determined as a cross product of three given planes AMDO 2006 No. slides 53 33

Computation in Projective Space • Note that we haven’t needed a division operation in above mentioned computations! • An “intersection of parallel lines” can be computed – it leads to [x, y, 0]T – that is a point in infinity • It leads to more robust computations in general - no IF clauses (conditions) are needed • Substantial speed up on CPU and GPU can be expected due to vector-vector operations support AMDO 2006 No. slides 53 34

Computation in Projective Space x 1 x 0 AMDO 2006 p A line in E 3 • as an intersection of two planes • parametric form • using Pluecker coordinates No. slides 53 35

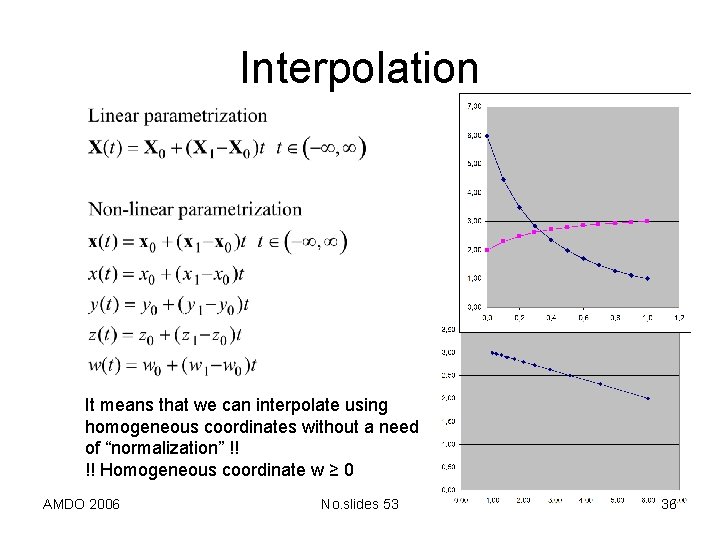
Interpolation It means that we can interpolate using homogeneous coordinates without a need of “normalization” !! !! Homogeneous coordinate w ≥ 0 AMDO 2006 No. slides 53 36

Barycentric coordinates Let us consider a triangle with vertices X 1, X 2, X 3, A position of any point X E 2 can be expressed as Linear system must be solved, if wi ≠ 1 then xi must be “normalized” AMDO 2006 No. slides 53 37

Barycentric coordinates It can be modified to: Rewriting AMDO 2006 No. slides 53 38

Barycentric coordinates if wi ≠ 1 AMDO 2006 No. slides 53 39

Barycentric coordinates if wi ≠ 1 It means that we can compute barycentric coordinates without division operation Simple modification for a position in tetrahedron [4] AMDO 2006 No. slides 53 40

Length, Area and Volume Length, area and volume computation in projective space if an element is given by points in homogeneous coordinates Line segment length Triangle area AMDO 2006 No. slides 53 41

Length, Area and Volume of a tetrahedron General formula AMDO 2006 No. slides 53 42

Intersection Computation in Projective Space x 1 Linear interpolation& parameterization very often used • intersection of a line and a plane • robustness problems if ATS → 0 p x 0 ? ? ? How to avoid an instability ? ? ? AMDO 2006 No. slides 53 43

Intersection Computation in Projective Space An intersection of a plane with a line in E 2 can be computed efficiently, more [6] Comparison operations must be modified !!! Cyrus-beck clipping algorithm 10% faster AMDO 2006 No. slides 53 44

Intersection Computation in Projective Space Line clipping in E 2 algorithms Cohen-Sutherland, Liang-Barsky Hodgman x 2 x 3 x. B x. A x 0 AMDO 2006 p x 1 procedure CLIP_L; {details in [3]} { x. A , x. B – in homogeneous coordinates } { The EXIT ends the procedure } { input: x. A , x. B } begin { x. A=[x. A, y. A, 1]T } {1} p : = x. A x x. B; { ax+by+c = 0; p = [a, b, c]T } {2} for k: =0 to N-1 do { xk=[xk, yk, 1]T } {3} if p. Txk 0 then ck: =1 else ck: =0; {4} if c = [0000]T or c = [1111]T then EXIT; {5} i: = TAB 1[c]; j: = TAB 2[c]; {6} x. A : = p x ei ; x. B : = p x ej ; {7} DRAW (x. A; x. B ) No. slides 53 45 end {CLIP_L};

Cg / HLSL and GPU Computing • GPU (Graphical Processing Unit) optimized for matrix-vector, vector-vector operation – especially for [x, y, z, w] Some CPU as well • Native arithmetic operations with homogeneous coordinates AMDO 2006 No. slides 53 46

Cg / HLSL and GPU Computing • 4 D cross product can be implemented in Cg/HLSL on GPU as: float 4 cross_4 D(float 4 x 1, float 4 x 2, float 4 x 3) { float 4 a; a. x=dot(x 1. yzw, cross(x 2. yzw, x 3. yzw)); a. y=-dot(x 1. xzw, cross(x 2. xzw, x 3. xzw)); a. z=dot(x 1. xyw, cross(x 2. xyw, x 3. xyw)); a. w=-dot(x 1. xyz, cross(x 2. xyz, x 3. xyz)); return a; } AMDO 2006 No. slides 53 47

Cg / HLSL and GPU Computing More compactly float 4 cross_4 D(float 4 x 1, float 4 x 2, float 4 x 3) { return ( dot(x 1. yzw, cross(x 2. yzw, x 3. yzw)), -dot(x 1. xzw, cross(x 2. xzw, x 3. xzw)), dot(x 1. xyw, cross(x 2. xyw, x 3. xyw)), -dot(x 1. xyz, cross(x 2. xyz, x 3. xyz)) ); } AMDO 2006 No. slides 53 48

Conclusion • Fundamentals of computation in projective space have been introduced • Proposed approach helps to improve robustness of intersection algorithms, nevertheless it does not give a solution limited numerical precision • Homogeneous coordinate must be non-negative • Comparison operations are a little bit complicated • Due to GPU and AMD CPU architecture algorithms might be significantly faster • Project supported by: – 3 DTV, project FP 6 Network of Excellence No. 511568 – VIRTUAL, project MSMT Czech Rep. , No. 2 C 06002 AMDO 2006 No. slides 53 49

Conclusion Future work • A new data type for programming languages – float_projective, double_projective should be considered – – perhaps as a native representation it enables to have more robust numerical algorithms unfortunately “doubles” a data bus traffic specific operation “exponent normalization” is needed and must be supported by a processor – experimental library of numerical and comparison operations AMDO 2006 No. slides 53 50

References [1] van Verth, J. M. , Bishop, L. M. : Essential Mathematics for Games and Interactive Applications, Morgan Kaufmann 2005 [2] Skala, V. : GPU Computation in Projective Space Using Homogeneous Coordinates, in Dickheiser, M. (Ed. ) Game Programming Gems 6, Charles River Media, 2006 [3] Skala, V. : A new approach to line and line segment clipping in homogeneous coordinates, The Visual Computer, Vol. 21, No. 11, pp. 905 -914, Springer Verlag, 2005 [4] Skala, V. : Barycentric coordinates computation in homogeneous coordinates, submitted for publication, 2006 [5] Skala, V. : Length, area and volume computation in homogenenous coordinates, accepted for publication, Journal of mage and Graphics, World Scientific Publ. Comp. , 2006 [6] Yamaguchi, F. : Computer Aided Design – A totally Four-Dimensional Approach, Springer Verlag 2002 [7] Fernando, R. , Kilgard, M. J. : The Cg Tutorial, Addison Wesley, 2003 AMDO 2006 No. slides 53 51

Thank you for your attention Your questions? AMDO 2006 No. slides 53 52

Contact Vaclav Skala skala@kiv. zcu. cz subj. AMDO 2006 http: //herakles. zcu. cz Center of Computer Graphics and Visualization, Department of informatics and Computer Science, Faculty of Applied Sciences, University of West Bohemia, Plzen, Czech Republic Please, feel free to visit our site on projects: http: //herakles. zcu. cz/grants/ European projects: http: //3 DTV. zcu. cz http: //Intuition. zcu. cz National projects: http: //LC-CPG. zcu. cz AMDO 2006 http: //MUTED. zcu. cz http: //Flash. Po. M. zcu. cz http: //VIRTUAL. zcu. cz No. slides 53 53