Computer vision models learning and inference Chapter 8














































- Slides: 67

Computer vision: models, learning and inference Chapter 8 Regression Please send errata to s. prince@cs. ucl. ac. uk

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 2

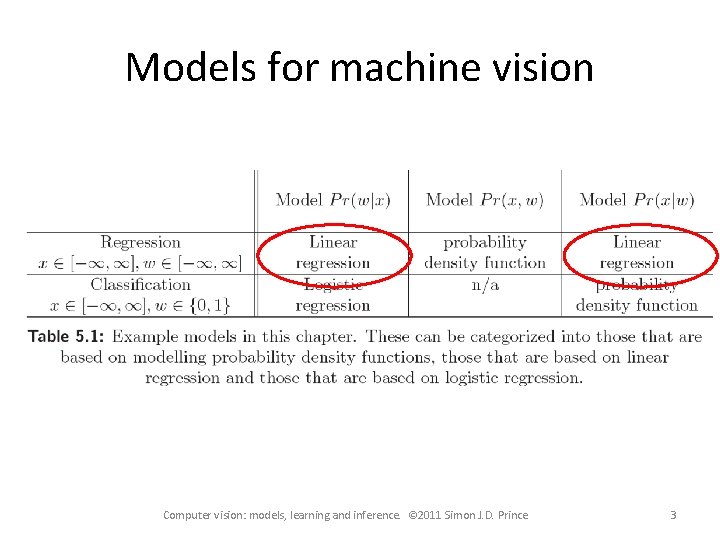
Models for machine vision Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 3

Body Pose Regression Encode silhouette as 100 x 1 vector, encode body pose as 55 x 1 vector. Learn relationship Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 4

Type 1: Model Pr(w|x) Discriminative How to model Pr(w|x)? – Choose an appropriate form for Pr(w) – Make parameters a function of x – Function takes parameters q that define its shape Learning algorithm: learn parameters q from training data x, w Inference algorithm: just evaluate Pr(w|x) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 5

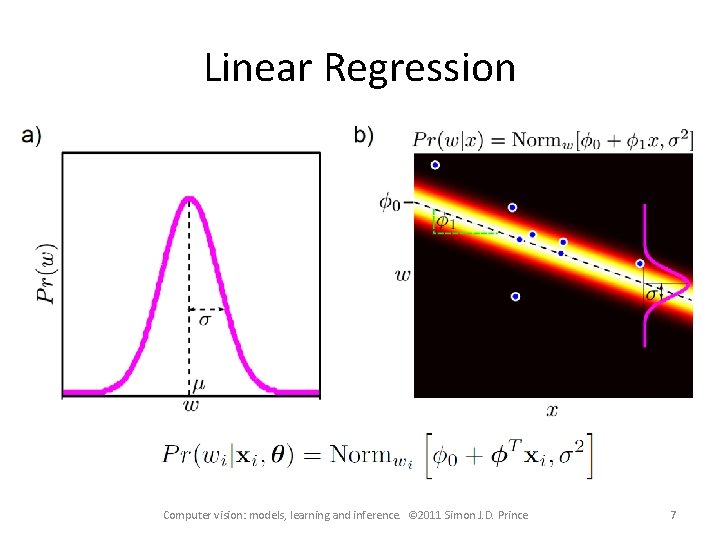
Linear Regression • • For simplicity we will assume that each dimension of world is predicted separately. Concentrate on predicting a univariate world state w. Choose normal distribution over world w Make • Mean a linear function of data x • Variance constant Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 6

Linear Regression Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 7

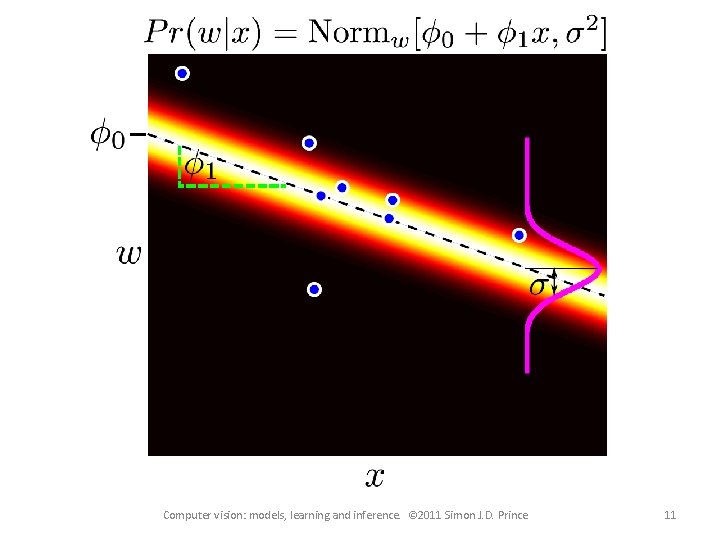
Neater Notation To make notation easier to handle, we • Attach a 1 to the start of every data vector • Attach the offset to the start of the gradient vector f New model: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 8

Combining Equations We have on equation for each x, w pair: The likelihood of the whole dataset is be the product of these individual distributions and can be written as where Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 9

Learning Maximum likelihood Substituting in Take derivative, set result to zero and re-arrange: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 10

Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 11

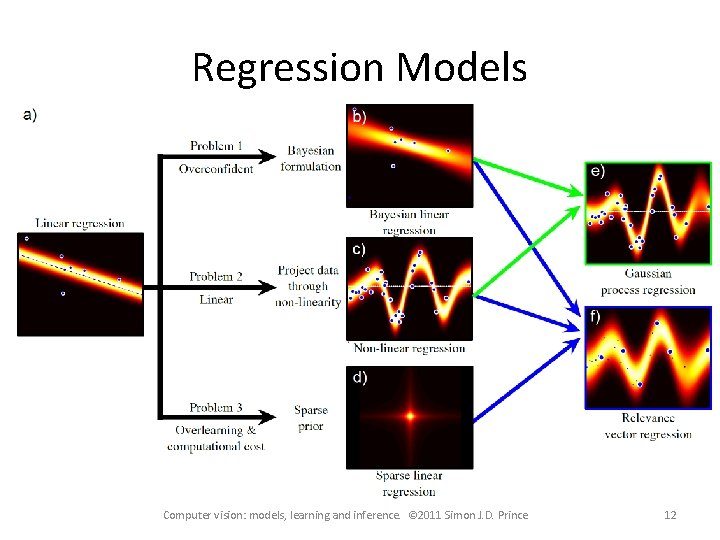
Regression Models Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 12

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 13

Bayesian Regression (We concentrate on f – come back to s 2 later!) Likelihood Prior Bayes rule’ Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 14

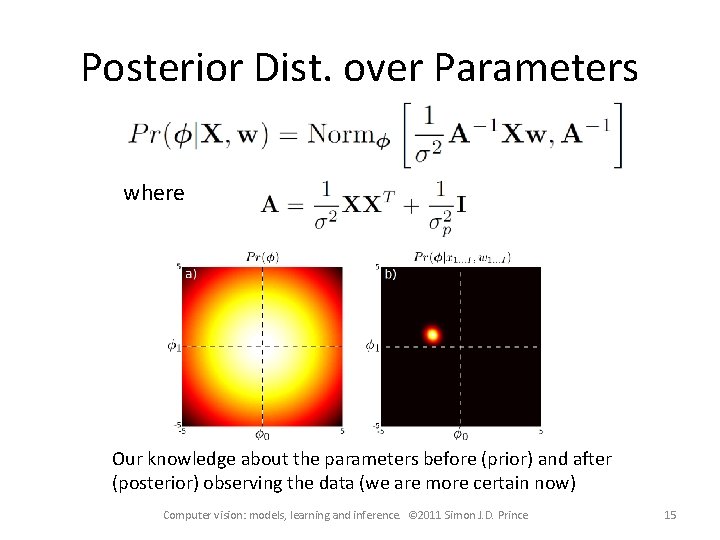
Posterior Dist. over Parameters where Our knowledge about the parameters before (prior) and after (posterior) observing the data (we are more certain now) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 15

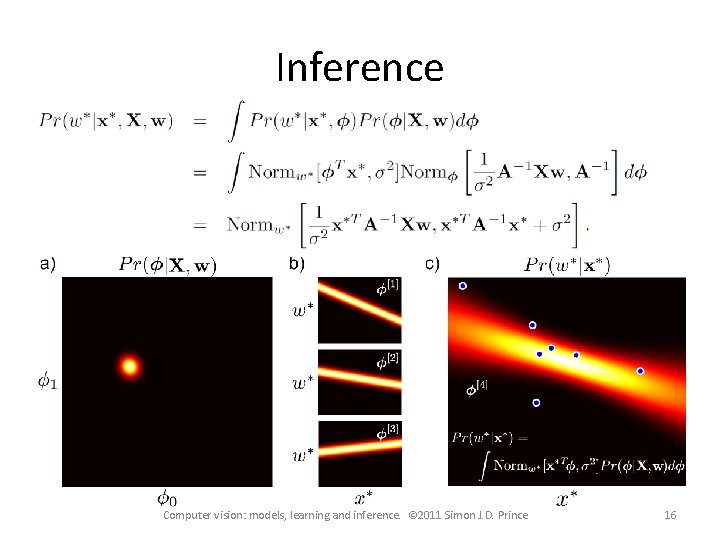
Inference Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 16

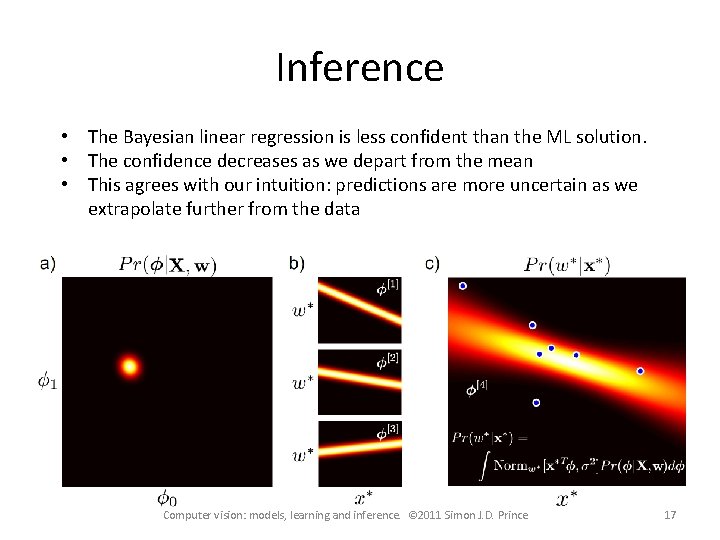
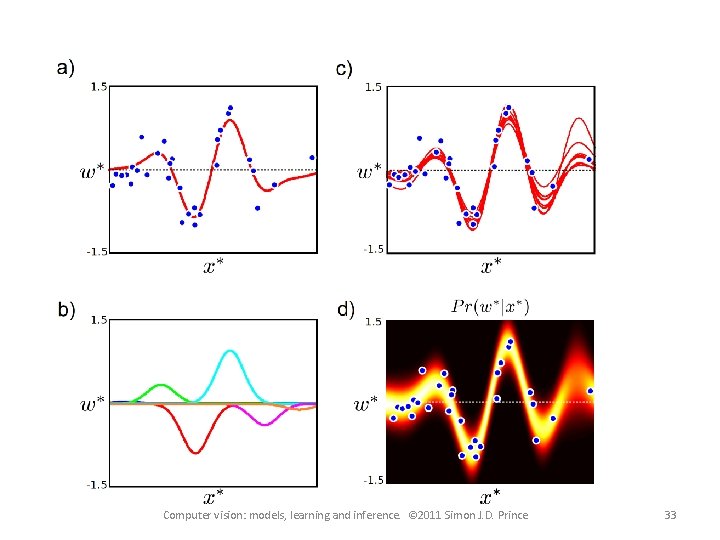
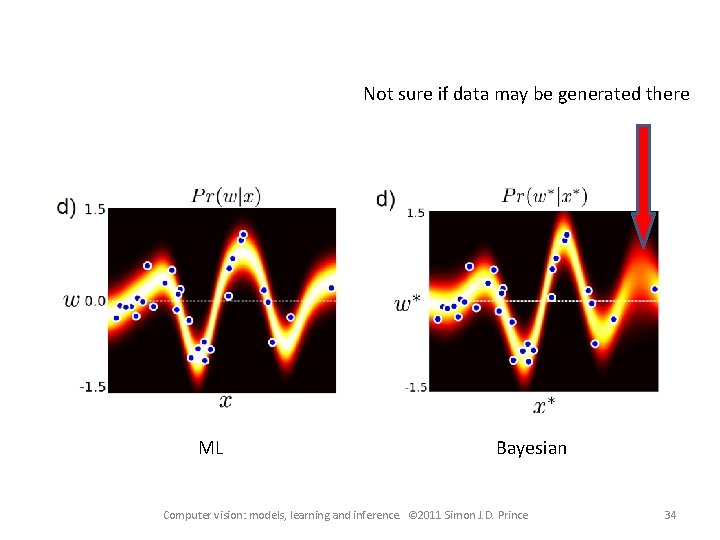
Inference • The Bayesian linear regression is less confident than the ML solution. • The confidence decreases as we depart from the mean • This agrees with our intuition: predictions are more uncertain as we extrapolate further from the data Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 17

Fitting Variance • We’ll fit the variance with maximum likelihood • Optimize the marginal likelihood (integrate out φ and maximize w. r. t. σ) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 18

Practical Issue Problem: In high dimensions, the matrix A may be too big to invert Solution: Re-express using Matrix Inversion Lemma Final expression: inverses are (I x I) , not (D x D) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 19

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 20

Regression Models Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 21

Non-Linear Regression The relation between data and world is generally non linear GOAL: Keep the maths of linear regression, but extend to more general functions KEY IDEA: You can make a non-linear function from a linear weighted sum of non-linear basis functions Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 22

Non-linear regression Linear regression: Non-Linear regression: where In other words create z by evaluating x against basis functions, then linearly regress against z. Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 23

Example: polynomial regression A special case of Where Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 24

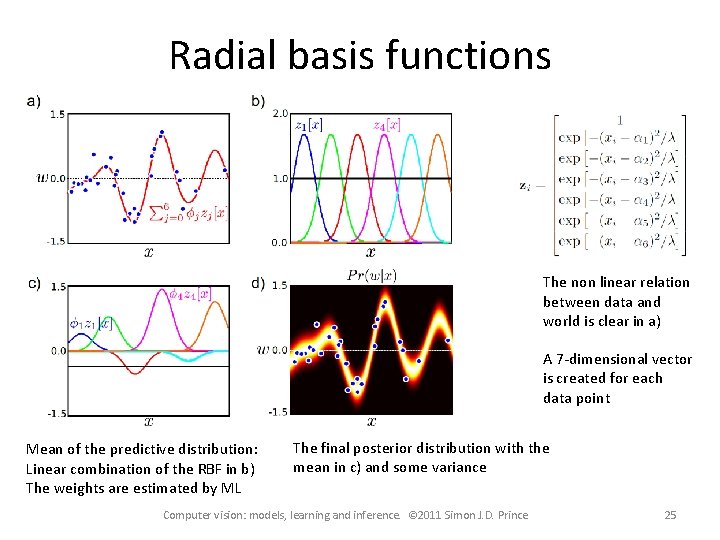
Radial basis functions The non linear relation between data and world is clear in a) A 7 -dimensional vector is created for each data point Mean of the predictive distribution: Linear combination of the RBF in b) The weights are estimated by ML The final posterior distribution with the mean in c) and some variance Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 25

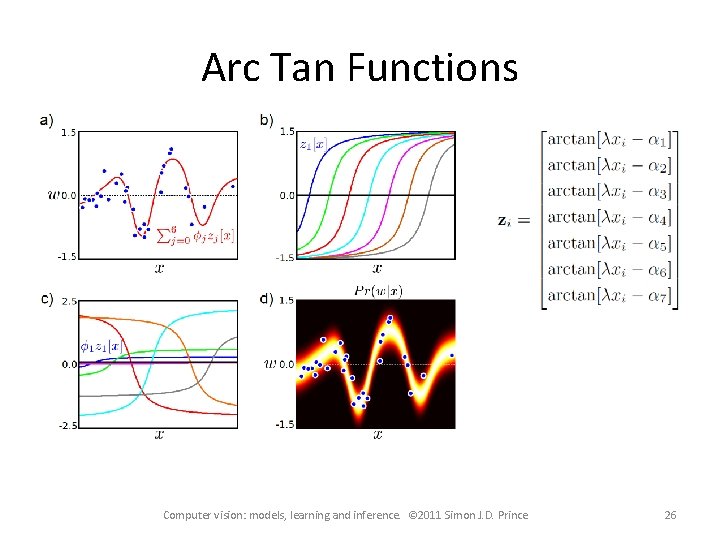
Arc Tan Functions Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 26

Non-linear regression Linear regression: Non-Linear regression: where In other words create z by evaluating x against basis functions, then linearly regress against z. Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 27

Non-linear regression Linear regression: Non-Linear regression: where In other words create z by evaluating against basis functions, Computer vision: models, learning andz. inference. © 2011 Simon J. D. Prince 28 then linearly regress against

Maximum Likelihood Same as linear regression, but substitute in Z for X: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 29

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 30

Regression Models Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 31

Bayesian Approach • The weights φ are treated as uncertain and are marginalized as in the linear case • Learn s 2 from marginal likelihood as before • Final predictive distribution: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 32

Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 33

Not sure if data may be generated there ML Bayesian Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 34

The Kernel Trick Notice that the final equation doesn’t need the data itself, but just dot products between data items of the form zi. Tzj So, we take data xi and xj pass through non-linear function to create zi and zj and then take dot products of different zi. Tzj Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 35

The Kernel Trick So, we take data xi and xj pass through non-linear function to create zi and zj and then take dot products of different zi. Tzj Key idea: Define a “kernel” function that does all of this together. • Takes data xi and xj • Returns a value for dot product zi. Tzj If we choose this function carefully, then it will corresponds to some underlying z=f[x]. Never compute z explicitly - can be very high or infinite dimension Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 36

Gaussian Process Regression Before After Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 37

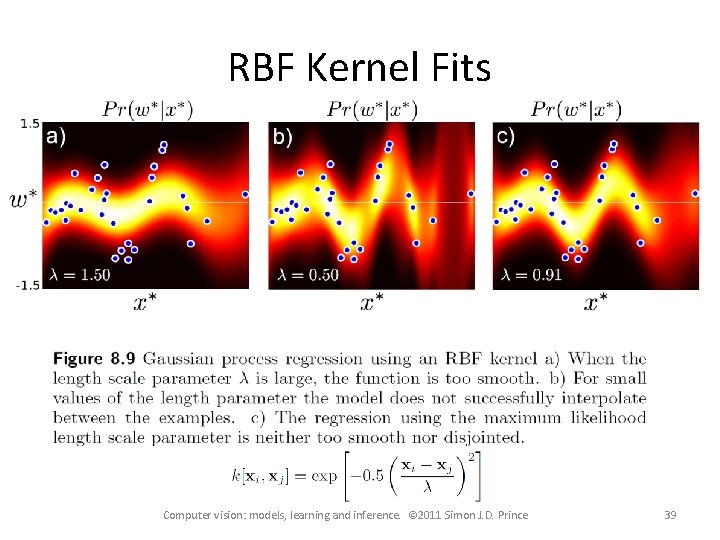
Example Kernels (Equivalent to having an infinite number of radial basis functions at every position in space. Wow!) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 38

RBF Kernel Fits Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 39

Fitting the kernel parameter λ • Optimize the marginal likelihood (likelihood after gradients have been integrated out) • Have to use non-linear optimization Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 40

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 41

Regression Models Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 42

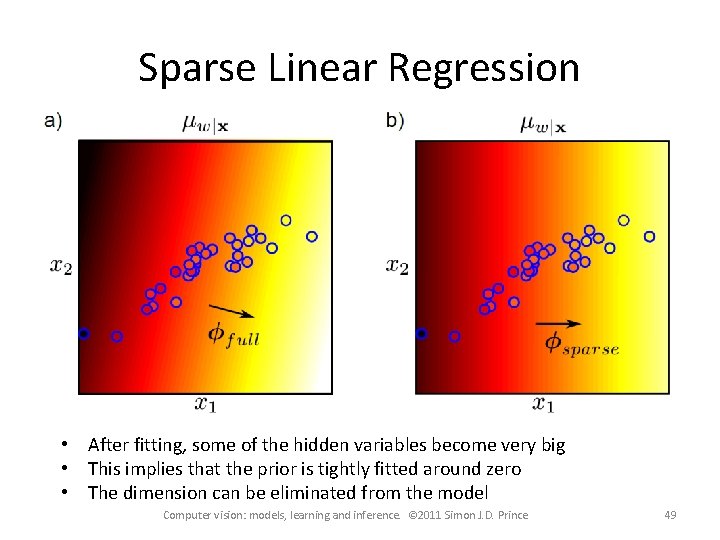
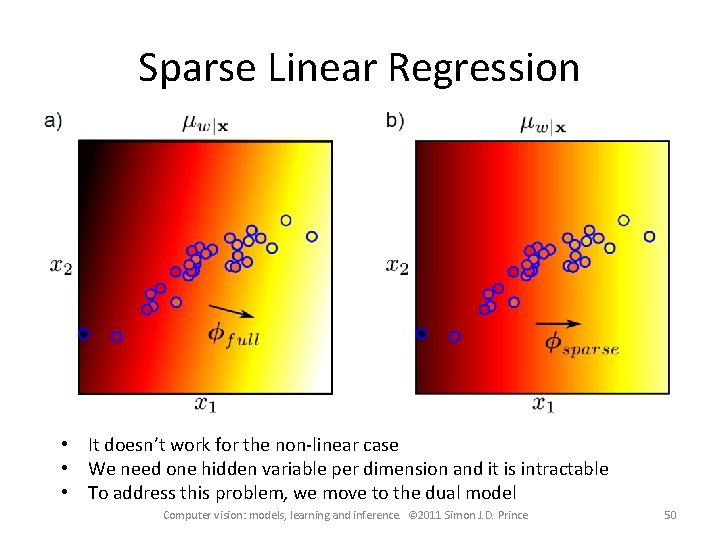
Sparse Linear Regression Perhaps not every dimension of the data x is informative A sparse solution forces some of the coefficients in f to be zero Method: – apply a different prior on f that encourages sparsity – product of t-distributions – ridges of high probability along the axes (sparsity as the other dimensions will be close to zero) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 43

Sparse Linear Regression Product of t-distributions to parameter vector (one per dimension): As before, we use Now the prior is not conjugate to the normal likelihood. Cannot compute posterior in closed from. We should do something different. Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 44

Sparse Linear Regression Write it as an infinite sum of normal with a hidden variable for the variances: Diagonal matrix with hidden variables {hd} on diagonal Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 45

Sparse Linear Regression We now forget the Bayesian approach for φ and approximate the marginal posterior (by integrating out φ) Still cannot compute, but can approximate Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 46

Sparse Linear Regression Still cannot compute, but can approximate • As long as H is distributed around the mode this is a good approximation • When h takes a large value, the variance οf φ will be small and the associated coefficient will be close to zero • The associated dimension of the data is not important Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 47

Sparse Linear Regression To fit the model, update variance s 2 and hidden variables {hd}. • The updated hidden variables • The updated variance: where Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 48

Sparse Linear Regression • After fitting, some of the hidden variables become very big • This implies that the prior is tightly fitted around zero • The dimension can be eliminated from the model Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 49

Sparse Linear Regression • It doesn’t work for the non-linear case • We need one hidden variable per dimension and it is intractable • To address this problem, we move to the dual model Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 50

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 51

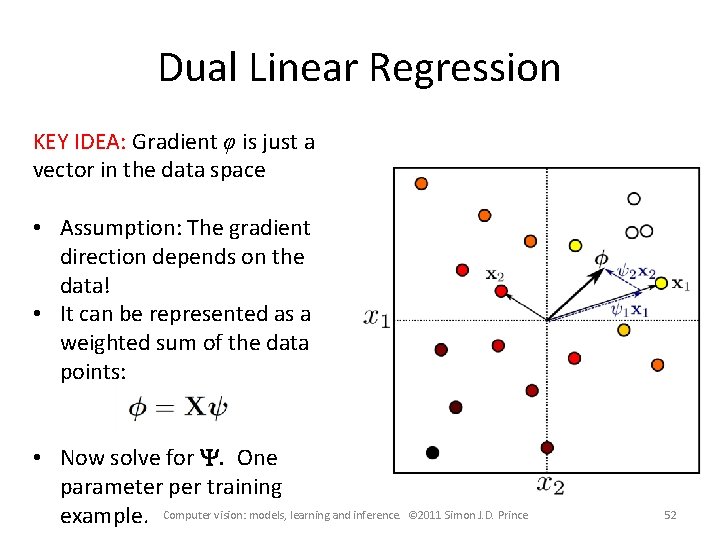
Dual Linear Regression KEY IDEA: Gradient φ is just a vector in the data space • Assumption: The gradient direction depends on the data! • It can be represented as a weighted sum of the data points: • Now solve for Y. One parameter per training example. Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 52

Dual Linear Regression Original linear regression: Dual variables: Dual linear regression: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 53

Maximum likelihood solution: Dual variables: Same result as before: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 54

Bayesian case Compute distribution over parameters: Gives result: where Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 55

Bayesian case Predictive distribution: where: Notice that in both the maximum likelihood and Bayesian case depend on dot products XTX. Can be kernelized! Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 56

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 57

Regression Models Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 58

Relevance Vector Machine Using same approximations as for sparse model we get the problem: To solve, update variance s 2 and hidden variables {hd} alternately. Notice that this only depends on dot-products and so can be kernelized Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 59

Relevance Vector Machine Combines ideas of • Dual regression (1 parameter per training example) • Sparsity (most of the parameters are zero) i. e. , model that only depends sparsely on training data. Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 60

Structure • • Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 61

Body Pose Regression using RVM (Agarwal and Triggs 2006) • Data x – 60 -dimensional shape context feature vector at each of the 500 silhouette points – Similarity between each feature and a codebook of 100 prototypes – 100 -dimensional histogram of similarities • World w – 55 dimensions: 3 joint angles of 18 major body joints + head orientation, Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 62

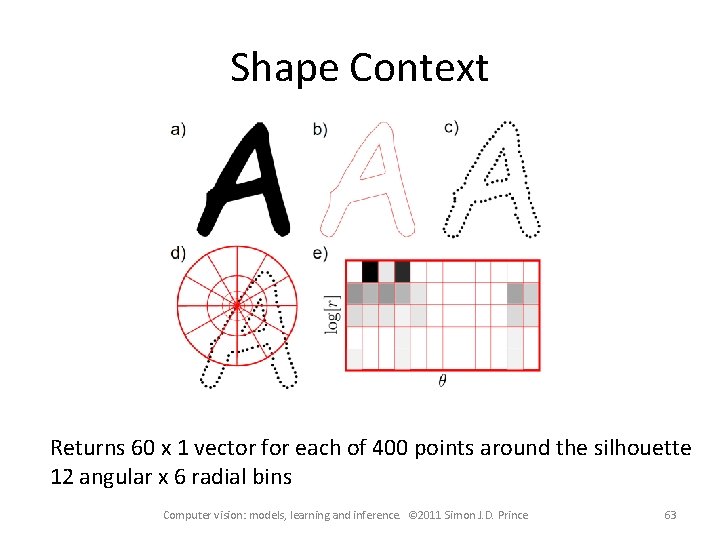
Shape Context Returns 60 x 1 vector for each of 400 points around the silhouette 12 angular x 6 radial bins Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 63

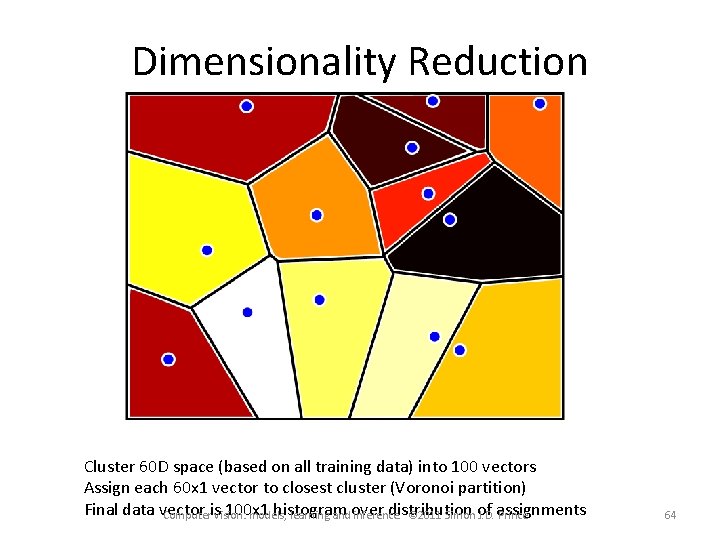
Dimensionality Reduction Cluster 60 D space (based on all training data) into 100 vectors Assign each 60 x 1 vector to closest cluster (Voronoi partition) Final data vector 100 x 1 histogram distribution Computeris vision: models, learning and over inference. © 2011 Simon of J. D. assignments Prince 64

Results • RVM regression to 2636 silhouettes extracted using POSER from known w • Only 6% of the input vectors are important • Average error of 6 degrees • The method works reasonably well on real images • Very hard to tell which leg is in front by looking at a silhouette – We need also to track the human body in a video sequence • The regressors presented in this chapter are unimodal – Multimodal regressors are more appropriate for this problem Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 65

Displacement experts • Data x – Translated versions of a bounding box around the object • World w – The translation vector Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 66

Regression • The main ideas all apply to classification: – Non-linear transformations – Kernelization – Dual parameters – Sparse priors Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 67
 Computer vision
Computer vision Computer vision models learning and inference
Computer vision models learning and inference Computer vision: models, learning, and inference pdf
Computer vision: models, learning, and inference pdf Computer vision: models, learning, and inference
Computer vision: models, learning, and inference Camera models in computer vision
Camera models in computer vision Camera models in computer vision
Camera models in computer vision Camera models in computer vision
Camera models in computer vision Human vision vs computer vision
Human vision vs computer vision Modals and semi modals difference
Modals and semi modals difference Cuadro comparativo e-learning m-learning b-learning
Cuadro comparativo e-learning m-learning b-learning Kubernetes vgpu
Kubernetes vgpu Concepts, techniques and models of computer programming
Concepts, techniques and models of computer programming Qm for windows
Qm for windows Mathematical foundations of computer graphics and vision
Mathematical foundations of computer graphics and vision Computer and robot vision
Computer and robot vision Self-paced learning for latent variable models
Self-paced learning for latent variable models Type of machine learning models
Type of machine learning models Geometric models in machine learning
Geometric models in machine learning Using inaccurate models in reinforcement learning
Using inaccurate models in reinforcement learning Stealing machine learning models via prediction apis
Stealing machine learning models via prediction apis Learning styles models
Learning styles models Stealing machine learning models via prediction apis
Stealing machine learning models via prediction apis Hsv model in computer graphics
Hsv model in computer graphics Parallel computer models
Parallel computer models Lighting models in computer graphics
Lighting models in computer graphics Computer graphics models are now commonly used for making
Computer graphics models are now commonly used for making Computational model
Computational model Bernstein condition for parallelism
Bernstein condition for parallelism Chapter 11 inference for distributions of categorical data
Chapter 11 inference for distributions of categorical data Chapter 12 inference for proportions answers
Chapter 12 inference for proportions answers Chapter 11 inference for distributions of categorical data
Chapter 11 inference for distributions of categorical data Chapter 11 inference for distributions of categorical data
Chapter 11 inference for distributions of categorical data Vision for learning tdsb
Vision for learning tdsb Vision for learning tdsb
Vision for learning tdsb 16385 cmu
16385 cmu Kalman filter computer vision
Kalman filter computer vision T11 computer
T11 computer Berkeley computer vision
Berkeley computer vision Multiple view geometry in computer vision
Multiple view geometry in computer vision Computer vision vs image processing
Computer vision vs image processing Radiometry in computer vision
Radiometry in computer vision Linear algebra for computer vision
Linear algebra for computer vision Impoverished motion examples
Impoverished motion examples Watershed segmentation
Watershed segmentation Computer vision stanford
Computer vision stanford Multiple view geometry in computer vision
Multiple view geometry in computer vision Azure computer vision python
Azure computer vision python Computer vision slides
Computer vision slides Ilsvrc-2012
Ilsvrc-2012 Computer vision final exam
Computer vision final exam Computer vision sift
Computer vision sift Multiple view geometry in computer vision
Multiple view geometry in computer vision Aperture problem computer vision
Aperture problem computer vision Computer vision vs nlp
Computer vision vs nlp Epipolar geometry computer vision
Epipolar geometry computer vision Computer vision camera calibration
Computer vision camera calibration Computer vision
Computer vision Computer vision
Computer vision Computer vision
Computer vision Computer vision
Computer vision Computer vision
Computer vision Computer vision
Computer vision Fourier transform computer vision
Fourier transform computer vision Image formation computer vision
Image formation computer vision Computer vision brown
Computer vision brown Computer vision brown
Computer vision brown Epipolar geometry computer vision
Epipolar geometry computer vision Computer vision brown
Computer vision brown






















































































