METODE NUMERIK SISTEM PERSAMAAN LINIER SIMULTAN Sistem Persamaan










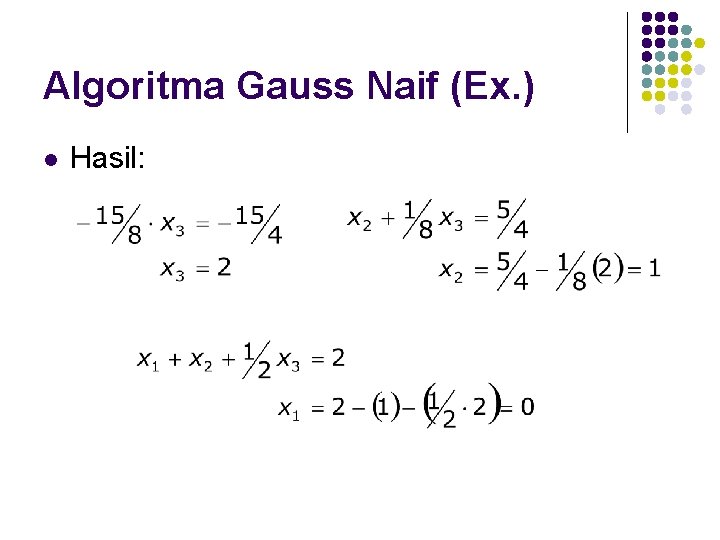





















- Slides: 32

METODE NUMERIK SISTEM PERSAMAAN LINIER SIMULTAN

Sistem Persamaan Linear l Misal terdapat SPL dengan n buah variabel bebas Matriks:

Penyelesaian Sistem Persamaan Linear (SPL) l l l Algoritma Gauss Naif Algoritma Gauss Jordan Algoritma Gauss Seidel

Algoritma Eliminasi Gauss/ Gauss Naif 1. 2. 3. Membagi persamaan pertama dengan koefisien a 11. Langkah tersebut disebut normalisasi. Tujuan normalisasi ini adalah agar koefisien dari x 1 berubah menjadi 1. Kalikan persamaan yang telah dinormalisasi (dalam hal ini persamaan pertama) dengan koefisien pertama dari persamaan kedua (yaitu a 21). Mengurangkan baris kedua dan ketiga dengan baris pertama.

Algoritma Gauss Naif 4. 5. 6. Kalikan persamaan pertama yang sudah dinormalisasi dengan koefisien tertentu sehingga a 11 = a 31. Kurangkan persamaan ketiga dengan hasil dari yang didapat dari langkah 4. Baris kedua dibagi dengan koefisien a 22. Langkah ini disebut NORMALISASI untuk persamaan kedua. Tujuannya adalah agar koefisien x 2 berubah menjadi 1.

Algoritma Gauss Naif 7. 8. Kalikan persamaan kedua yang sudah dinormalisasi pada langkah ke-6 dengan suatu koefisien tertentu sehingga a 22 = a 32. Kurangkan persamaan ketiga dengan persamaan kedua hasil dari langkah ke-7.

Algoritma Gauss Naif (Ex. ) l l Diketahui SPL: 2 x 1 + 2 x 2 + x 3 = 4 3 x 1 - x 2 + x 3 = 1 x 1 + 4 x 2 - x 3 = 2 Bagaimana penyelesaiannya?

Algoritma Gauss Naif (Ex. ) l Matriks yang terbentuk: l Langkah: 1.

Algoritma Gauss Naif (Ex. ) 2. dan 3. 4. dan 5.

Algoritma Gauss Naif (Ex. ) 6. 7. dan 8.
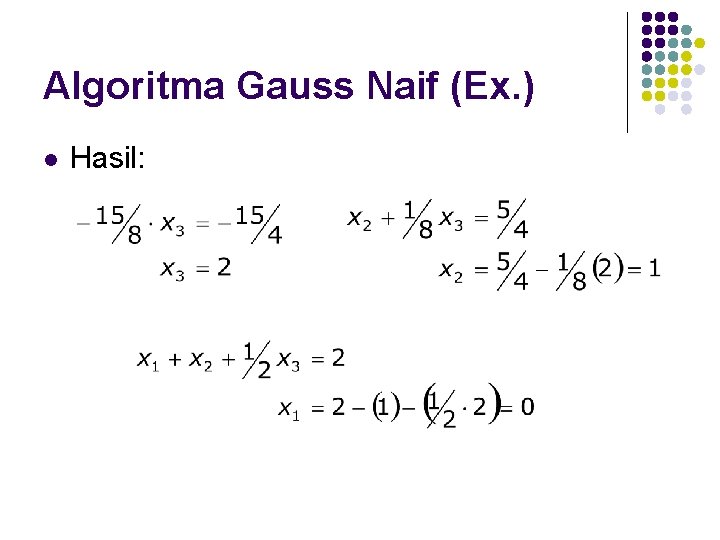
Algoritma Gauss Naif (Ex. ) l Hasil:

Algoritma Gauss Jordan l Dengan metode Gauss Jordan matriks A diubah sedemikian rupa sampai terbentuk identitas dengan cara : diubah menjadi C* merupakan matriks C yang sudah mengalami beberapa kali transformasi, sehingga:

Algoritma Gauss Jordan (Ex. ) l l Diketahui SPL: 2 x 1 + 2 x 2 + x 3 = 4 3 x 1 - x 2 + x 3 = 1 x 1 + 4 x 2 - x 3 = 2 Bagaimana penyelesaiannya?

Algoritma Gauss Jordan (Ex. ) l Langkah: 1. 2.

Algoritma Gauss Jordan (Ex. ) 3. 4.

Algoritma Gauss Jordan (Ex. ) 5. 6.

Algoritma Gauss Jordan (Ex. ) 7. Jadi: x 1 = 0, x 2 = 1, x 3 = 2

Tugas l l Selesaikan persamaan linier simultan dibawah ini dengan Algorithma Eliminasi Gauss dan Eliminasi Gauss Jordan. Selesaikan menggunakan Excel.

Algoritma Gauss Seidel l l Sering dipakai untuk menyelesaikan persamaan yang berjumlah besar. Dilakukan dengan suatu iterasi yang memberikan harga awal untuk x 1 = x 2 = x 3 =. . . = xn = 0. Metode ini berlainan dengan metode Gauss Jordan Gauss Naif karena metode ini menggunakan iterasi dalam menentukan harga x 1, x 2, x 3, . . . , xn. Kelemahan metode eliminasi dibandingkan metode iterasi adalah metode eliminasi sulit untuk digunakan dalam menyelesaikan SPL berukuran besar.

Algoritma Gauss Seidel 1. 2. Beri harga awal x 1 = x 2 = x 3 =. . . = xn = 0 Hitung Karena x 2 = x 3 = x 4 =. . . = xn = 0, maka

Algoritma Gauss Seidel 3. x 1 baru yang didapat dari tahap 2 digunakan untuk menghitung x 2. Baris 2 a 21 x 1 + a 22 x 2 + a 23 x 3 +. . . + a 2 nxn = C 2

Algoritma Gauss Seidel 4. Menghitung x 3 Baris 3 a 31 x 1 + a 32 x 2 + a 33 x 3 +. . . + a 3 nxn = C 3 a 33 x 3 = C 3 – a 31 x 1 – a 32 x 2 – … – a 3 nxn

Algoritma Gauss Seidel 5. 6. Cara ini diteruskan sampai ditemukan xn. Lakukan iterasi ke-2 untuk menghitung x 1, x 2, x 3, . . . , xn baru

Algoritma Gauss Seidel 7. Mencari kesalahan iterasi | a| dengan cara: 8. Iterasi diteruskan sampai didapat | a| < | s|

Algoritma Gauss Seidel (Ex. ) l Diketahui SPL: x 1 + 7 x 2 – 3 x 3 = – 51 4 x 1 – 4 x 2 + 9 x 3 = 61 12 x 1 – x 2 + 3 x 3 = 8 dan a = 5 %

Algoritma Gauss Seidel (Ex. ) l l Iterasi ke-0 x 1 = x 2 = x 3 = 0 Iterasi ke-1

Algoritma Gauss Seidel (Ex. ) l Iterasi ke-2

Algoritma Gauss Seidel (Ex. ) l Iterasi ke-3 l Perhitungan x 1, x 2, x 3 diteruskan sampai semua | a| < | s|

Algoritma Gauss Seidel (Ex. ) a Iterasi ke- Nilai x 0 x 1 = 0 x 2 = 0 x 3 = 0 1 x 1 = 51 x 2 = 66, 25 x 3 = 184, 58 2 x 1 = 966, 49 x 2 = 1366, 55 x 3 = 3407, 78 a = 105, 28 % a = 104, 85 % a = 105, 42 % 3 x 1 = 19840, 19 x 2 = 27522, 94 x 3 = 70189, 11 a = 104, 87 % a = 104, 97 % a = 104, 86 %

Koefisien Relaksasi ( ) l l Tujuan: Perbaikan konvergensi dalam Gauss Seidel. Biasanya koefisien relaksasi dipilih sendiri berdasarkan masalah yang dihadapi. Jika SPL tidak konvergen, yang bernilai antara 0 s/d 1 disebut Under Relaksasi. antara 1 dan 2 biasanya digunakan untuk mempercepat konvergensi suatu sistem persamaan yang konvergen, disebut Over Relaksasi.

Koefisien Relaksasi ( ) l Rumus (nilai SPL) dengan menggunakan

Koefisien Relaksasi ( ) (Ex. ) Iterasi ke 0 1 2 3 Nilai x dengan (1, 5) x 1 = 0 x 2 = 0 x 1 = 10 x 2 = 15 x 1 = 6 x 1 baru = 4 x 2 = 7, 5 x 2 baru = 3, 75 x 1 = 4 x 2 = 3, 75 Contoh perhitungan : x 1 baru = 1, 5. 6 + (1 – 1, 5). 10 = 9 + (– 0, 5). 10 =4
 Contoh soal dan penyelesaian metode iterasi gauss -seidel
Contoh soal dan penyelesaian metode iterasi gauss -seidel Contoh soal metode regula falsi
Contoh soal metode regula falsi Penyelesaian persamaan simultan
Penyelesaian persamaan simultan Eliminasi gauss
Eliminasi gauss Simultaneous equations graphical method
Simultaneous equations graphical method Non linear simultaneous equations
Non linear simultaneous equations Pencarian akar akar persamaan linear
Pencarian akar akar persamaan linear Metode tertutup metode numerik
Metode tertutup metode numerik Persamaan non linier metode biseksi
Persamaan non linier metode biseksi Algoritma metode euler
Algoritma metode euler Contoh soal metode tabel
Contoh soal metode tabel Contoh persamaan simultan
Contoh persamaan simultan Persamaan simultan
Persamaan simultan Persamaan diferensial simultan
Persamaan diferensial simultan Perbedaan regresi linier dan non linier
Perbedaan regresi linier dan non linier Trend eksponensial
Trend eksponensial Contoh soal dan jawaban trend non linier
Contoh soal dan jawaban trend non linier Contoh soal fungsi non linier
Contoh soal fungsi non linier Nonlinear function
Nonlinear function Fungsi non linier dan contohnya
Fungsi non linier dan contohnya Diketahui sistem persamaan linear
Diketahui sistem persamaan linear Angka penting
Angka penting Contoh soal integrasi numerik
Contoh soal integrasi numerik Contoh soal integrasi numerik metode simpson
Contoh soal integrasi numerik metode simpson Diferensiasi numerik metode selisih maju
Diferensiasi numerik metode selisih maju Kesalahan pemotongan metode numerik
Kesalahan pemotongan metode numerik Interpolasi adalah
Interpolasi adalah Metode numerik teknik informatika
Metode numerik teknik informatika Metode numerik
Metode numerik Hampiran adalah
Hampiran adalah Metode numerik
Metode numerik 0,000454 memiliki …. angka penting
0,000454 memiliki …. angka penting Metode ekstrapolasi richardson
Metode ekstrapolasi richardson



















































