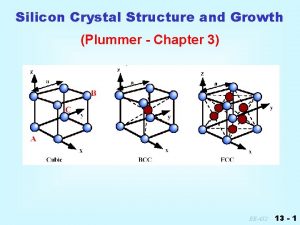
Crystal Structure Continued NOTE Much of the discussion














- Slides: 42

Crystal Structure Continued! • NOTE!! Much of the discussion & many figures in what follows were constructed from lectures posted on the web by Prof. Beşire GÖNÜL in Turkey. She has done an excellent job of covering many details of crystallography & she illustrates her topics with many very nice pictures of lattice structures. Her lectures on this are posted Here: http: //www 1. gantep. edu. tr/~bgonul/dersnotlari/. Her homepage is Here: http: //www 1. gantep. edu. tr/~bgonul/.

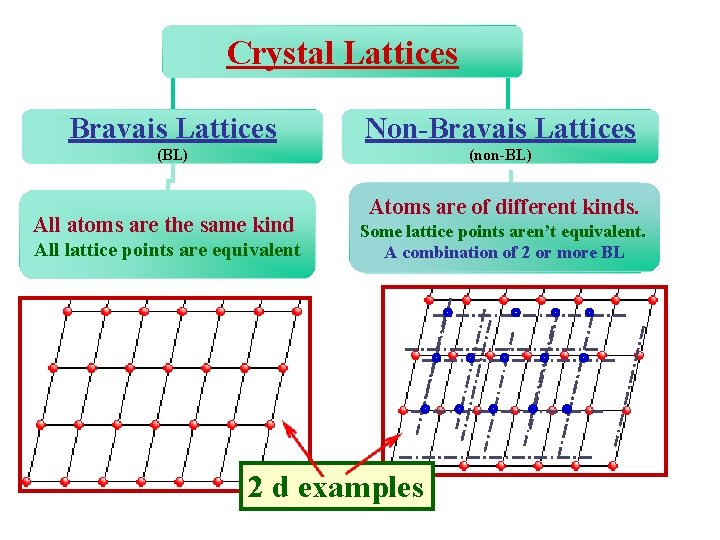
Crystal Lattices Bravais Lattices Non-Bravais Lattices (BL) (non-BL) All atoms are the same kind All lattice points are equivalent Atoms are of different kinds. Some lattice points aren’t equivalent. Atoms are of different kinds. Some A combination 2 or more BL lattice points areofnot equivalent. 2 d examples

Lattice Translation Vectors In General • Mathematically, a lattice is defined by 3 vectors called Primitive Lattice Vectors a 1, a 2, a 3 are 3 d vectors which depend on the geometry. • Once a 1, a 2, a 3 are specified, the Primitive Lattice Structure is known. • The infinite lattice is generated by translating through a Direct Lattice Vector: T = n 1 a 1 + n 2 a 2 + n 3 a 3 n 1, n 2, n 3 are integers. T generates the lattice points. Each lattice point corresponds to a set of integers (n 1, n 2, n 3).

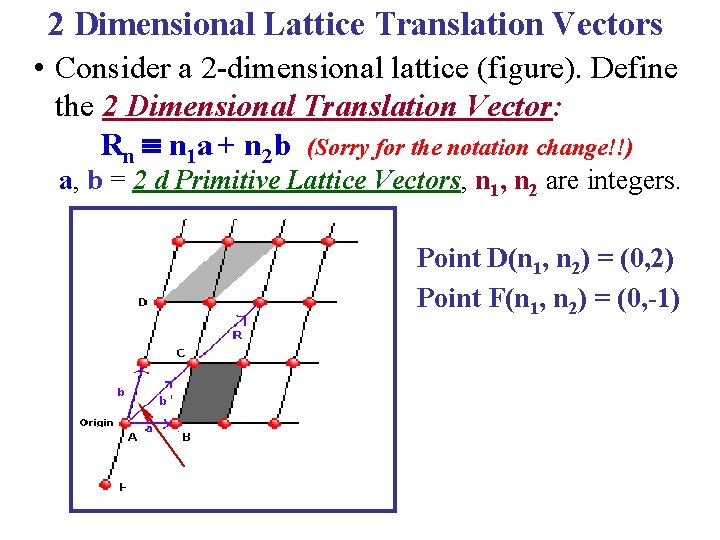
2 Dimensional Lattice Translation Vectors • Consider a 2 -dimensional lattice (figure). Define the 2 Dimensional Translation Vector: Rn n 1 a + n 2 b (Sorry for the notation change!!) a, b = 2 d Primitive Lattice Vectors, n 1, n 2 are integers. Point D(n 1, n 2) = (0, 2) Point F(n 1, n 2) = (0, -1)

2 Dimensional Lattice Translation Vectors • Consider a 2 -dimensional lattice (figure). Define the 2 Dimensional Translation Vector: Rn n 1 a + n 2 b (Sorry for the notation change!!) a, b = 2 d Primitive Lattice Vectors, n 1, n 2 are integers. Point D(n 1, n 2) = (0, 2) Point F(n 1, n 2) = (0, -1) • Once a & b are specified by the lattice geometry & an origin is chosen, all symmetrically equivalent points in the lattice are determined by the translation vector Rn. That is, the lattice has translational symmetry. • Note that the choice of Primitive Lattice vectors is not unique! So, one could equally well take vectors a & b' as primitive lattice vectors.

The Basis (or basis set) The set of atoms which, when placed at each lattice point, generates the Crystal Structure ≡ Primitive Lattice + Basis Translate the basis through all possible lattice vectors T = n 1 a 1 + n 2 a 2 + n 3 a 3 to get the Crystal Structure or the Direct Lattice

• The periodic lattice symmetry is such that the atomic arrangement looks the same from an arbitrary vector position r as when viewed from the point r' = r + T (1) where T is the translation vector for the lattice: T = n 1 a 1 + n 2 a 2 + n 3 a 3 • Mathematically, the lattice & the vectors a 1, a 2, a 3 are Primitive if any 2 points r & r' always satisfy (1) with a suitable choice of integers n 1, n 2, n 3.

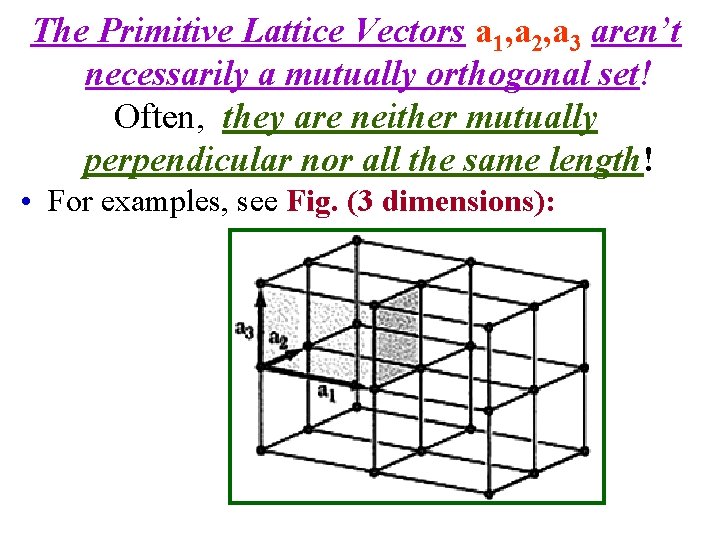
• In 3 dimensions, no 2 of the 3 primitive lattice vectors a 1, a 2, a 3 can be along the same line. But, DO NOT think of a 1, a 2, a 3 as a mutually orthogonal set! Often, they are neither mutually perpendicular nor all the same length! • For examples, see Fig. (2 dimensions):

The Primitive Lattice Vectors a 1, a 2, a 3 aren’t necessarily a mutually orthogonal set! Often, they are neither mutually perpendicular nor all the same length! • For examples, see Fig. (3 dimensions):

Crystal Lattice Types Bravais Lattice • An infinite array of discrete points with an arrangement & orientation that appears exactly the same, from whichever of the points the array is viewed. A Bravais Lattice is invariant under a translation T = n 1 a 1 + n 2 a 2 + n 3 a 3 Nb film

Non-Bravais Lattices • In a Bravais Lattice, not only the atomic arrangement but also the orientations must appear exactly the same from every lattice point. • This is not true for a non-Bravais Lattice.

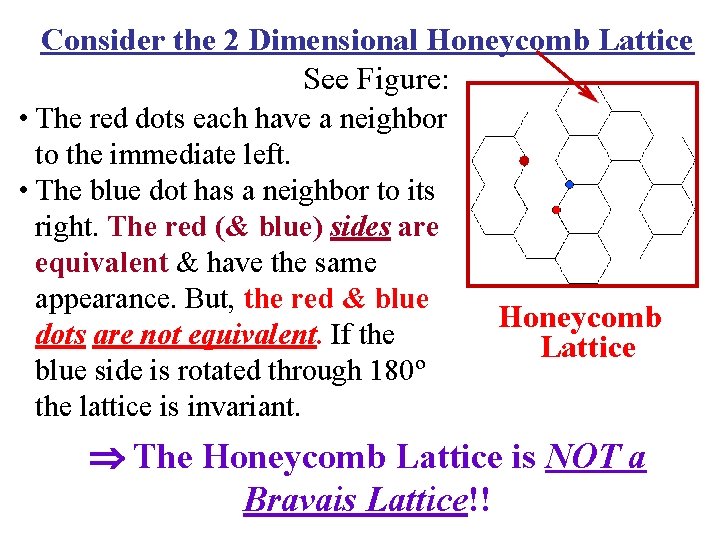
Consider the 2 Dimensional Honeycomb Lattice See Figure: • The red dots each have a neighbor to the immediate left. • The blue dot has a neighbor to its right. The red (& blue) sides are equivalent & have the same appearance. But, the red & blue dots are not equivalent. If the blue side is rotated through 180º the lattice is invariant. Honeycomb Lattice The Honeycomb Lattice is NOT a Bravais Lattice!!

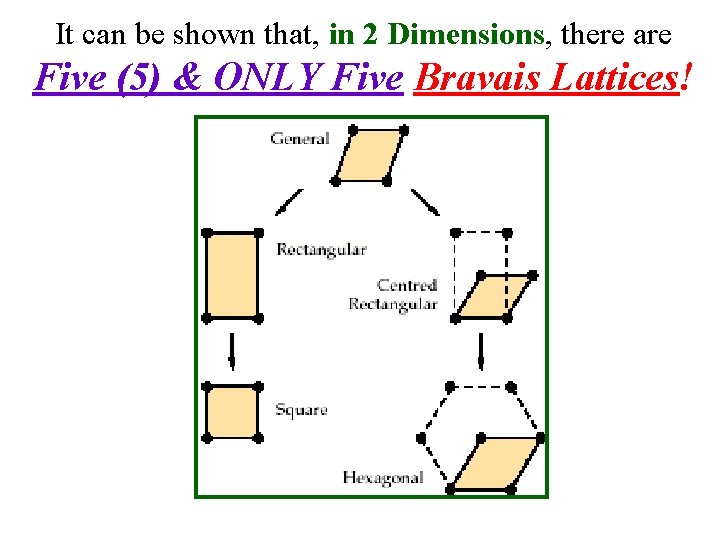
It can be shown that, in 2 Dimensions, there are Five (5) & ONLY Five Bravais Lattices!

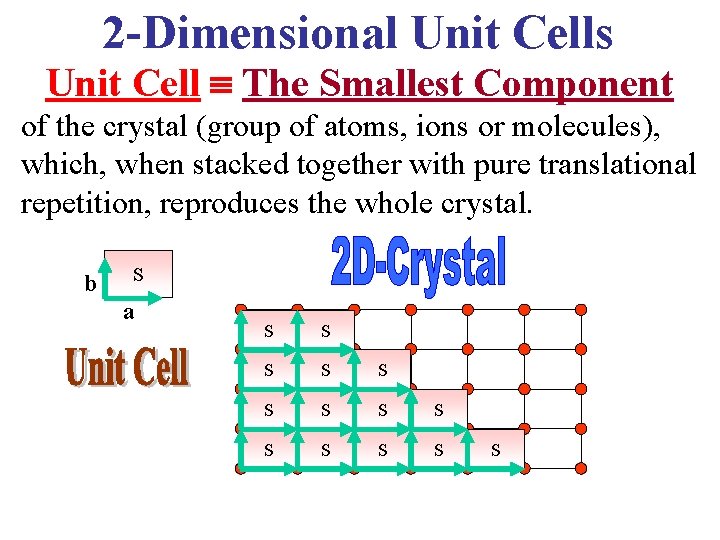
2 -Dimensional Unit Cells Unit Cell The Smallest Component of the crystal (group of atoms, ions or molecules), which, when stacked together with pure translational repetition, reproduces the whole crystal. b S a S S S S

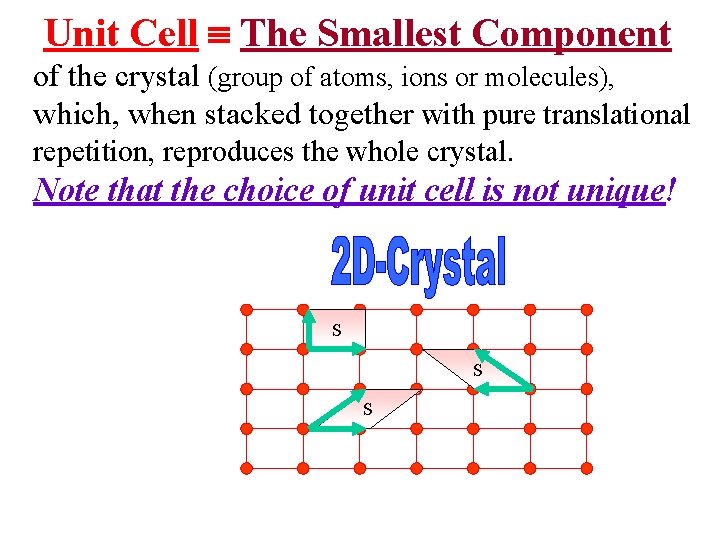
Unit Cell The Smallest Component of the crystal (group of atoms, ions or molecules), which, when stacked together with pure translational repetition, reproduces the whole crystal. Note that the choice of unit cell is not unique! S S S

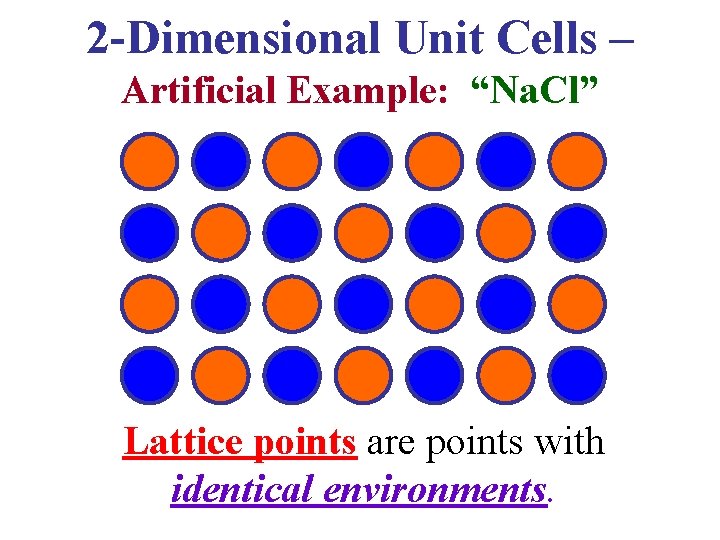
2 -Dimensional Unit Cells – Artificial Example: “Na. Cl” Lattice points are points with identical environments.

2 -Dimensional Unit Cells: “Na. Cl” Note that the choice of origin is arbitrary! the lattice points need not be atoms, but The unit cell size must always be the same.

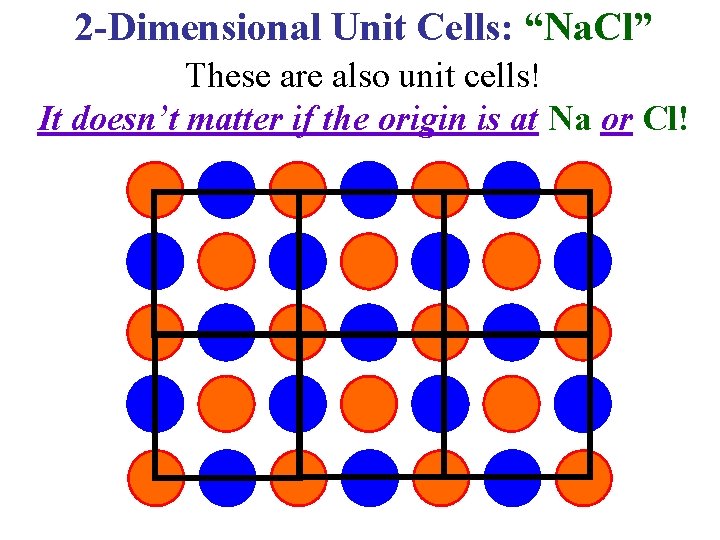
2 -Dimensional Unit Cells: “Na. Cl” These are also unit cells! It doesn’t matter if the origin is at Na or Cl!

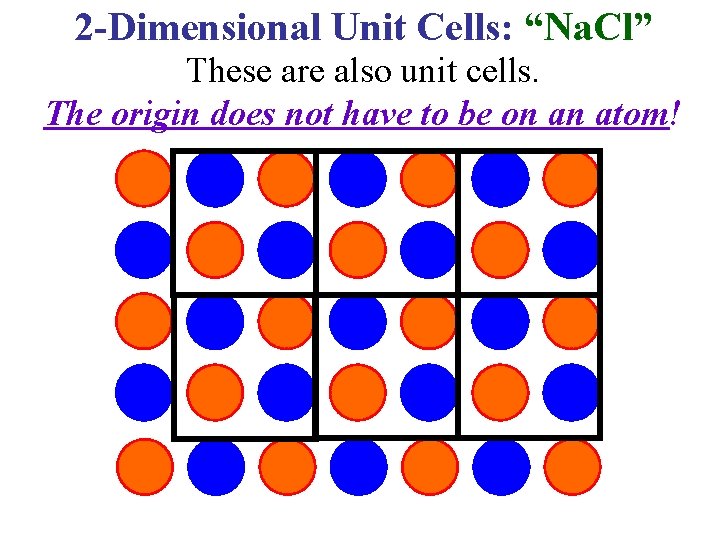
2 -Dimensional Unit Cells: “Na. Cl” These are also unit cells. The origin does not have to be on an atom!

2 -Dimensional Unit Cells: “Na. Cl” These are NOT unit cells! Empty space is not allowed!

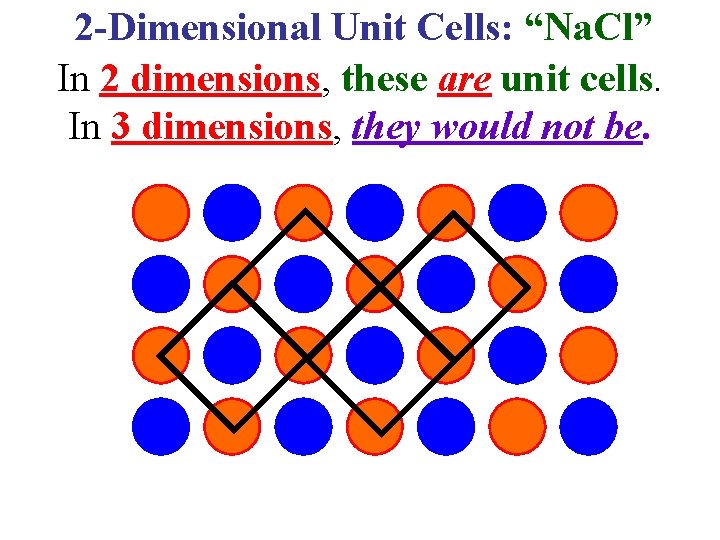
2 -Dimensional Unit Cells: “Na. Cl” In 2 dimensions, these are unit cells. In 3 dimensions, they would not be.

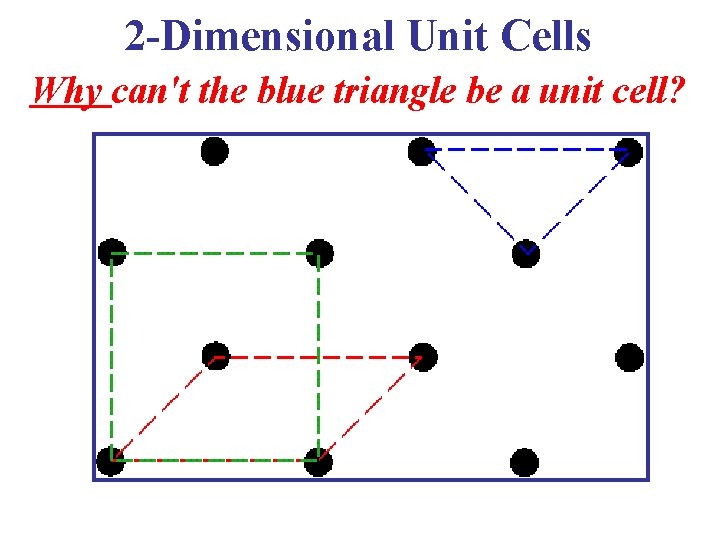
2 -Dimensional Unit Cells Why can't the blue triangle be a unit cell?

Example: 2 Dimensional, Periodic Art! A Painting by Dutch Artist Maurits Cornelis Escher (1898 -1972) Escher was famous for his so called “impossible structures”, such as Ascending & Descending, Relativity, . . Can you find the “Unit Cell” in this painting?

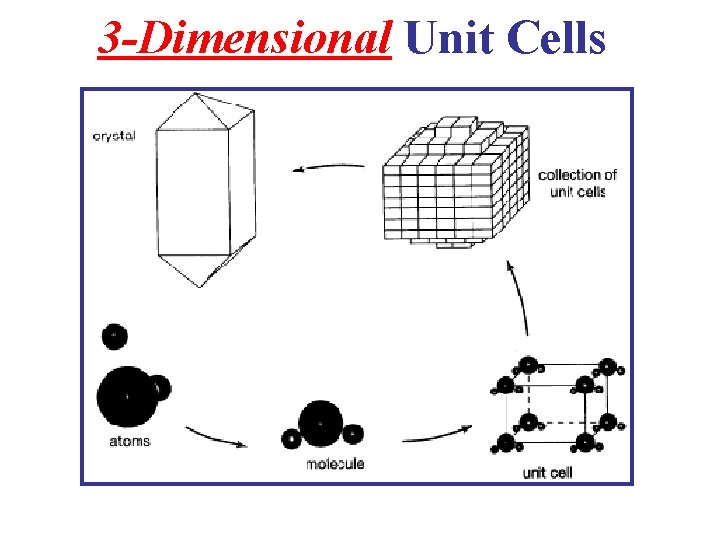
3 -Dimensional Unit Cells

3 -Dimensional Unit Cells

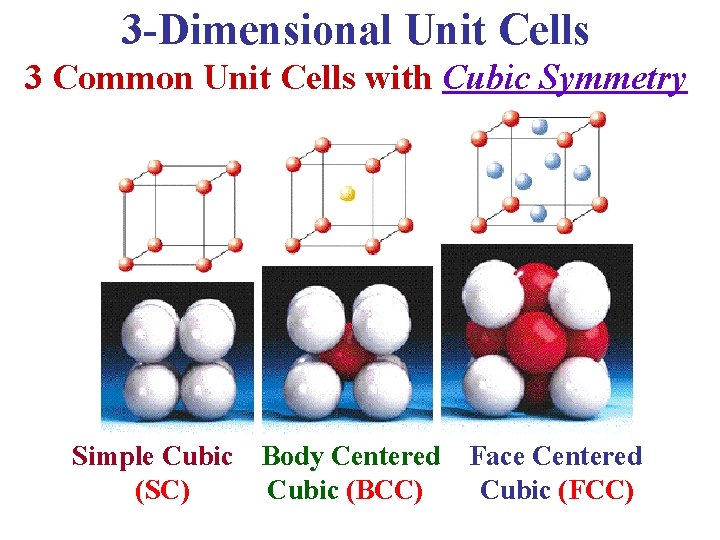
3 -Dimensional Unit Cells 3 Common Unit Cells with Cubic Symmetry Simple Cubic (SC) Body Centered Cubic (BCC) Face Centered Cubic (FCC)

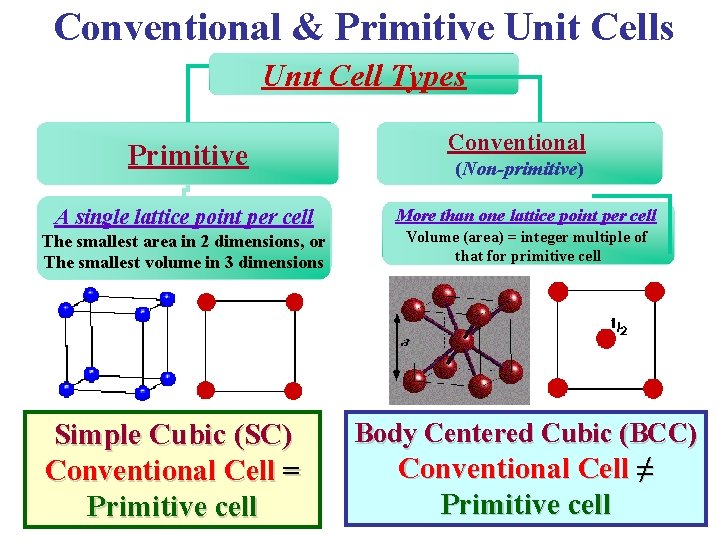
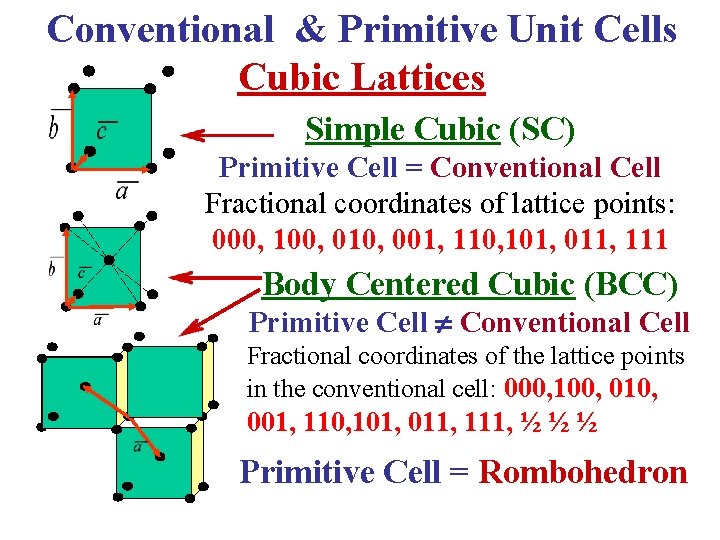
Conventional & Primitive Unit Cells Unıt Cell Types Primitive A single lattice point per cell The smallest area in 2 dimensions, or The smallest volume in 3 dimensions Simple Cubic (SC) Conventional Cell = Primitive cell Conventional (Non-primitive) More than one lattice point per cell Volume (area) = integer multiple of that for primitive cell Body Centered Cubic (BCC) Conventional Cell ≠ Primitive cell

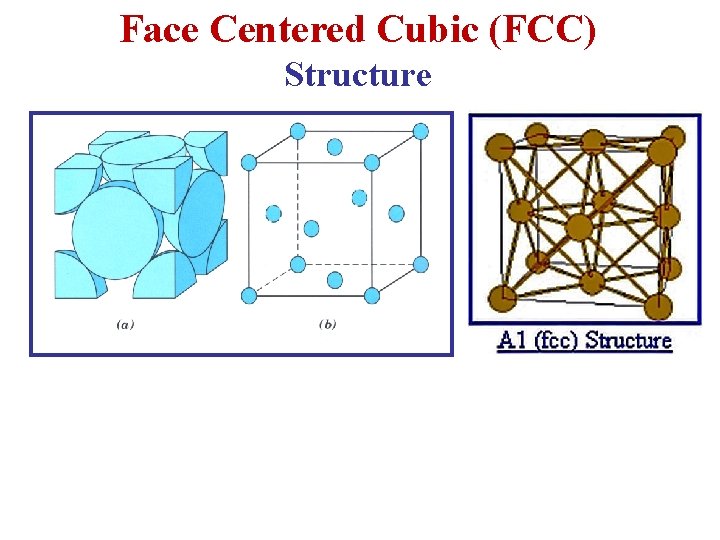
Face Centered Cubic (FCC) Structure

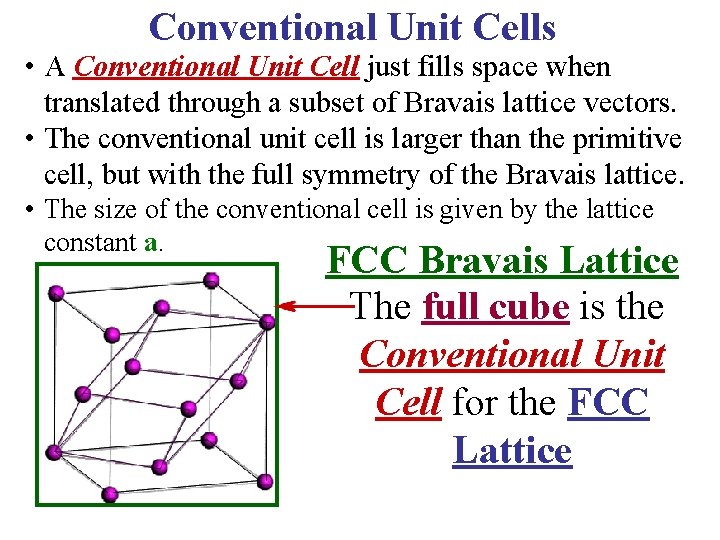
Conventional Unit Cells • A Conventional Unit Cell just fills space when translated through a subset of Bravais lattice vectors. • The conventional unit cell is larger than the primitive cell, but with the full symmetry of the Bravais lattice. • The size of the conventional cell is given by the lattice constant a. FCC Bravais Lattice The full cube is the Conventional Unit Cell for the FCC Lattice

Conventional & Primitive Unit Cells Face Centered Cubic Lattice Primitive Unit Cell (Shaded) Lattice Const. Primitive Lattice Vectors a 1 = (½)a(0, 1, 1) a 2 = (½)a(1, 0, 1) a 3 = (½)a(1, 1, 0) Note that the ai’s are Conventional Unit Cell (Full Cube) NOT Mutually Orthogonal!

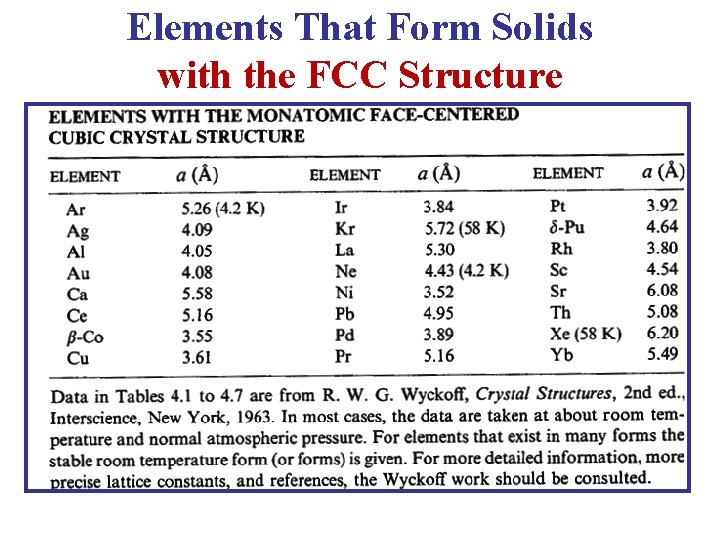
Elements That Form Solids with the FCC Structure

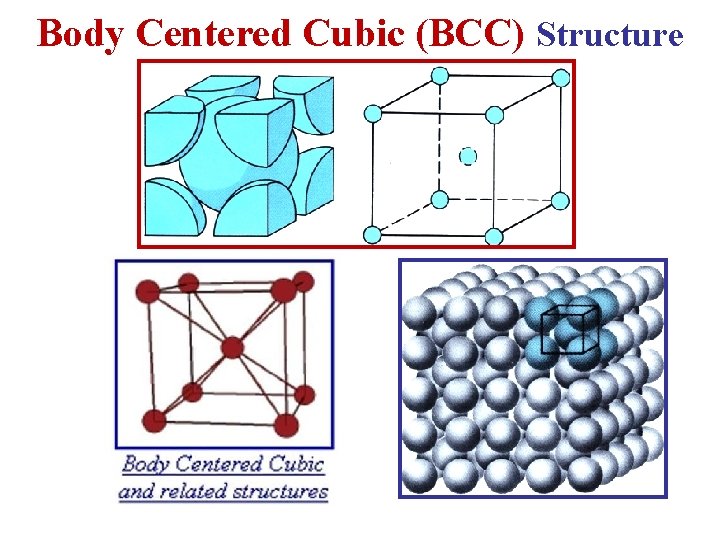
Body Centered Cubic (BCC) Structure

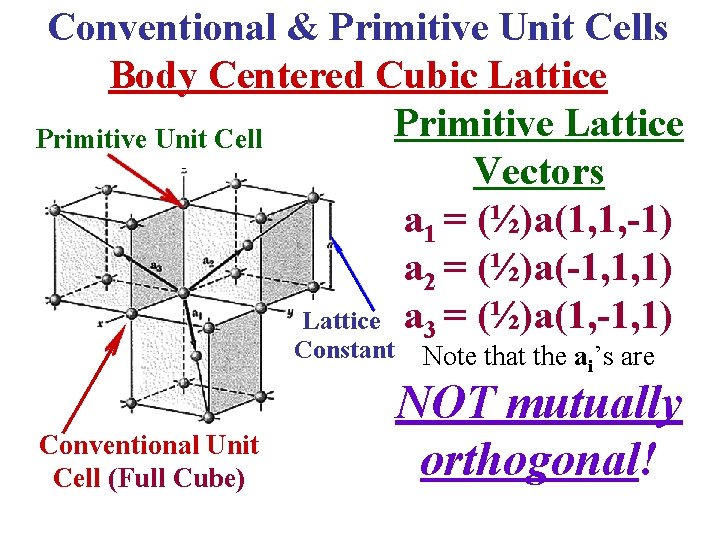
Conventional & Primitive Unit Cells Body Centered Cubic Lattice Primitive Unit Cell Vectors a 1 = (½)a(1, 1, -1) a 2 = (½)a(-1, 1, 1) Lattice a 3 = (½)a(1, -1, 1) Constant Conventional Unit Cell (Full Cube) Note that the ai’s are NOT mutually orthogonal!

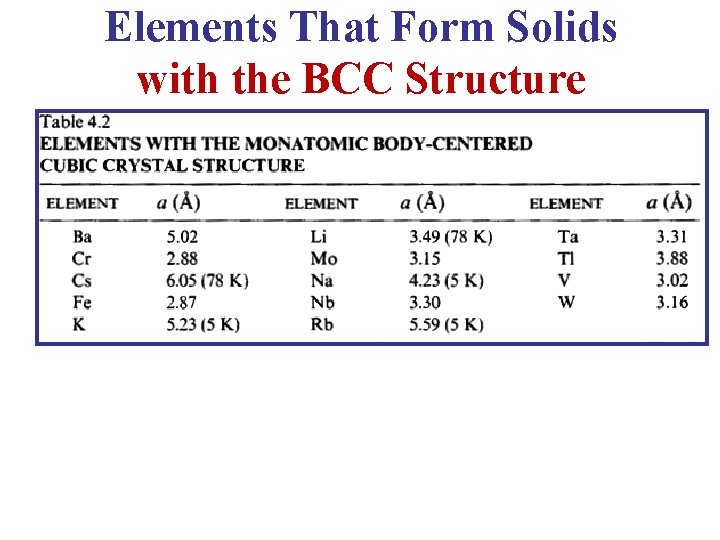
Elements That Form Solids with the BCC Structure

Conventional & Primitive Unit Cells Cubic Lattices Simple Cubic (SC) Primitive Cell = Conventional Cell Fractional coordinates of lattice points: 000, 100, 010, 001, 110, 101, 011, 111 Body Centered Cubic (BCC) Primitive Cell Conventional Cell Fractional coordinates of the lattice points in the conventional cell: 000, 100, 010, 001, 110, 101, 011, 111, ½ ½ ½ Primitive Cell = Rombohedron

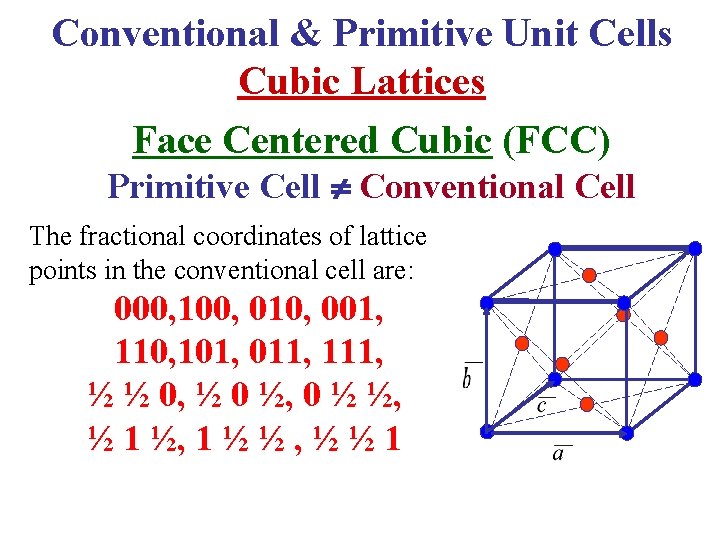
Conventional & Primitive Unit Cells Cubic Lattices Face Centered Cubic (FCC) Primitive Cell Conventional Cell The fractional coordinates of lattice points in the conventional cell are: 000, 100, 010, 001, 110, 101, 011, 111, ½ ½ 0, ½ 0 ½, 0 ½ ½, ½ 1 ½, 1 ½ ½ , ½ ½ 1

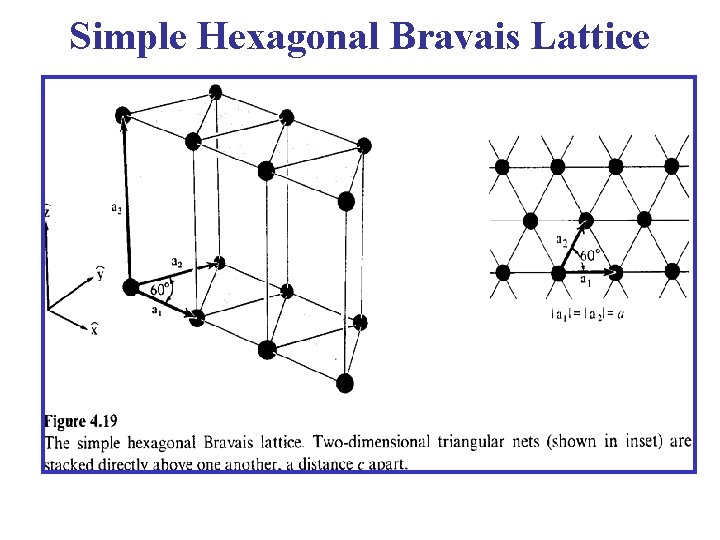
Simple Hexagonal Bravais Lattice

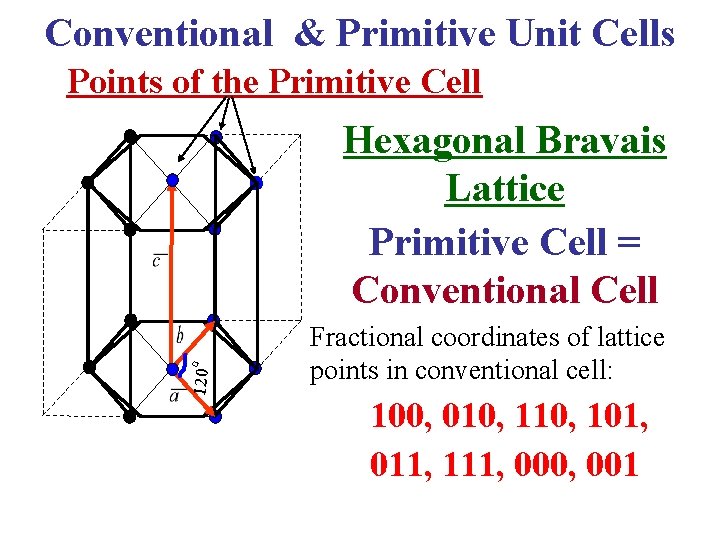
Conventional & Primitive Unit Cells Points of the Primitive Cell 120 o Hexagonal Bravais Lattice Primitive Cell = Conventional Cell Fractional coordinates of lattice points in conventional cell: 100, 010, 101, 011, 111, 000, 001

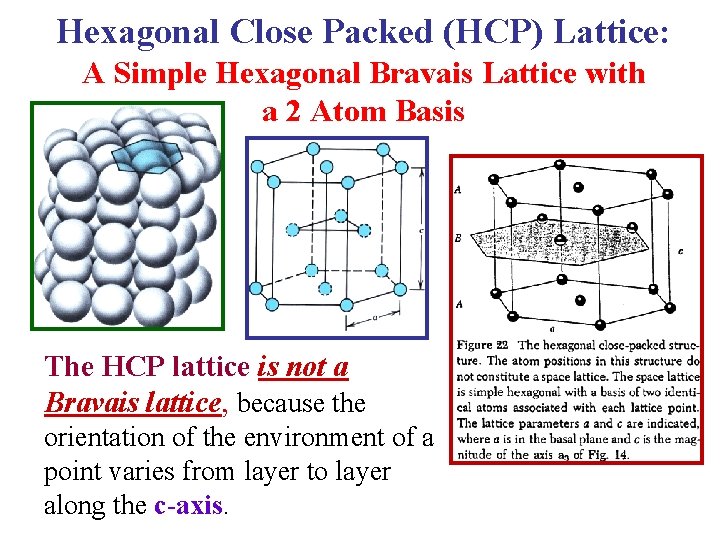
Hexagonal Close Packed (HCP) Lattice: A Simple Hexagonal Bravais Lattice with a 2 Atom Basis The HCP lattice is not a Bravais lattice, because the orientation of the environment of a point varies from layer to layer along the c-axis.

General Unit Cell Discussion • For any lattice, the unit cell &, thus, the entire lattice, is UNIQUELY determined by 6 constants (figure): a, b, c, α, β and γ which depend on lattice geometry. • As we’ll see, we sometimes want to calculate the number of atoms in a unit cell. To do this, imagine stacking hard spheres centered at each lattice point & just touching each neighboring sphere. Then, for the cubic lattices, only 1/8 of each lattice point in a unit cell is assigned to that cell. In the cubic lattice in the figure, Each unit cell is associated with (8) (1/8) = 1 lattice point.

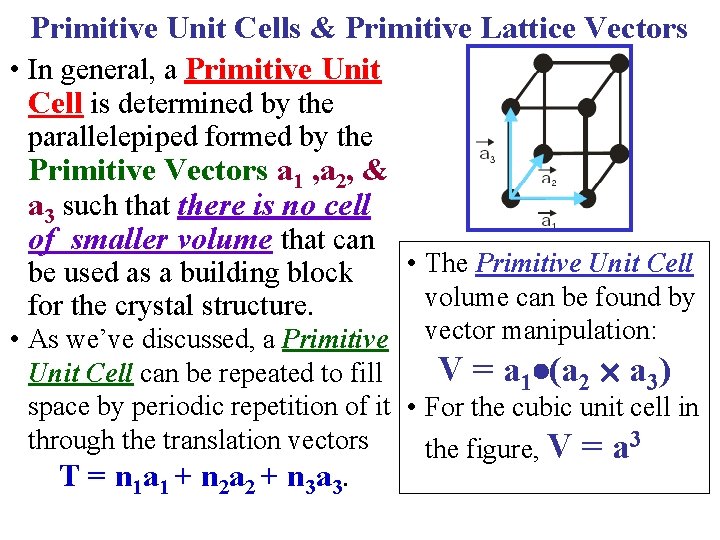
Primitive Unit Cells & Primitive Lattice Vectors • In general, a Primitive Unit Cell is determined by the parallelepiped formed by the Primitive Vectors a 1 , a 2, & a 3 such that there is no cell of smaller volume that can • The Primitive Unit Cell volume can be found by • As we’ve discussed, a Primitive vector manipulation: V = a 1 (a 2 a 3) Unit Cell can be repeated to fill space by periodic repetition of it • For the cubic unit cell in through the translation vectors the figure, V = a 3 be used as a building block for the crystal structure. T = n 1 a 1 + n 2 a 2 + n 3 a 3.

Primitive Unit Cells • Note that, by definition, the Primitive Unit Cell must contain ONLY ONE lattice point. • There can be different choices for the Primitive Lattice Vectors, but the Primitive Cell volume must be independent of that choice. 2 Dimensional Example! P = Primitive Unit Cell NP = Non-Primitive Unit Cell
 Simple distillation discussion
Simple distillation discussion After much discussion
After much discussion Difference between note making and note taking
Difference between note making and note taking Signal word
Signal word Difference between note making and note taking
Difference between note making and note taking Goods received note
Goods received note Debit note format
Debit note format How to write debit note
How to write debit note Note making advantages
Note making advantages A simple discount note results in
A simple discount note results in How much beats is a quarter note
How much beats is a quarter note How much caffeine in a snickers bar
How much caffeine in a snickers bar To whom much is given much is required meaning
To whom much is given much is required meaning How much is too much plagiarism
How much is too much plagiarism Zns crystal structure unit cell
Zns crystal structure unit cell Silicon unit cell
Silicon unit cell Titanium crystal structure
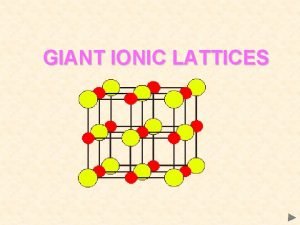
Titanium crystal structure Giant ionic crystal lattice
Giant ionic crystal lattice Bcc crystal structure
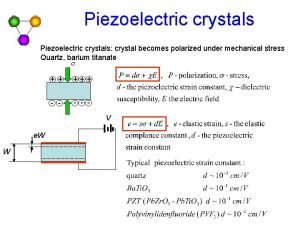
Bcc crystal structure Piezoelectric crystal atomic structure
Piezoelectric crystal atomic structure Basis in crystal structure
Basis in crystal structure Crystal structure of ceramics
Crystal structure of ceramics Ideal crystals have
Ideal crystals have Metallic crystal structure
Metallic crystal structure Atomic packing factor for bcc
Atomic packing factor for bcc Motif in material science
Motif in material science How to write a discussion text
How to write a discussion text The world is too much with us figurative language
The world is too much with us figurative language Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Chó sói
Chó sói Thang điểm glasgow
Thang điểm glasgow Chúa yêu trần thế alleluia
Chúa yêu trần thế alleluia Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tính độ biến thiên đông lượng
Công thức tính độ biến thiên đông lượng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Cách giải mật thư tọa độ
Cách giải mật thư tọa độ Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Phản ứng thế ankan
Phản ứng thế ankan