The Most Important Crystal Structures The Most Important

The “Most Important” Crystal Structures

The “Most Important” Crystal Structures • NOTE!! Much of the discussion & many figures in what follows were again constructed from lectures posted on the web by Prof. Beşire GÖNÜL in Turkey. She has done an excellent job of covering many details of crystallography & she illustrates her topics with many very nice pictures of lattice structures. Her lectures on this are posted Here: http: //www 1. gantep. edu. tr/~bgonul/dersnotlari/. Her homepage: http: //www 1. gantep. edu. tr/~bgonul/.

The “Most Important” Crystal Structures • Sodium Chloride Structure Na+Cl • Cesium Chloride Structure Cs+Cl • Hexagonal Closed-Packed Structure • Diamond Structure • Zinc Blende Structure 4

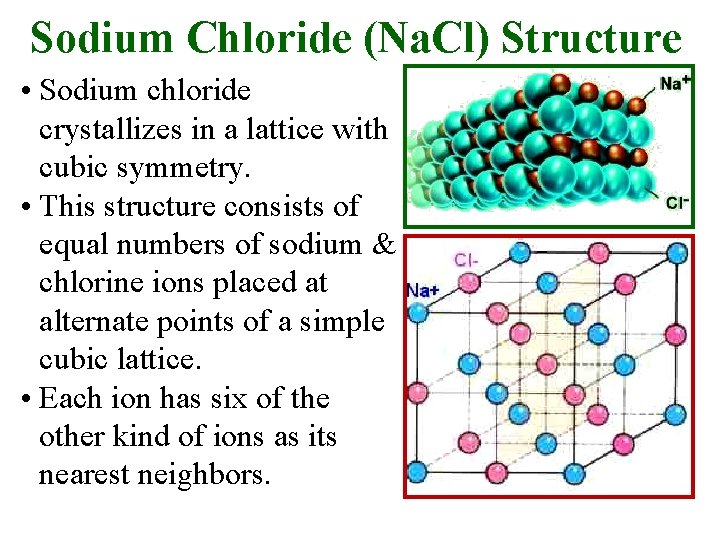
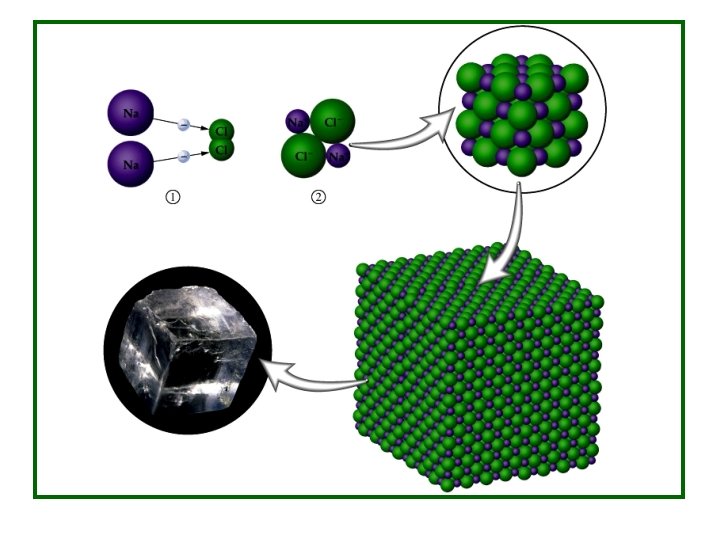
Sodium Chloride (Na. Cl) Structure • Sodium chloride crystallizes in a lattice with cubic symmetry. • This structure consists of equal numbers of sodium & chlorine ions placed at alternate points of a simple cubic lattice. • Each ion has six of the other kind of ions as its nearest neighbors.

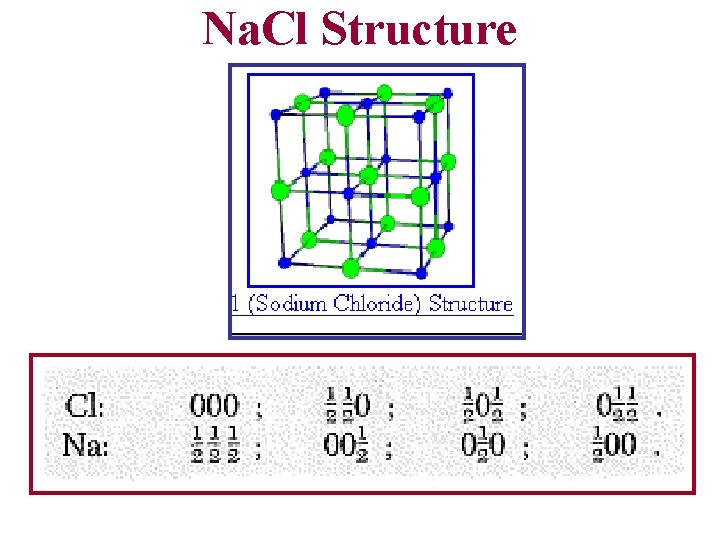
Na. Cl Structure

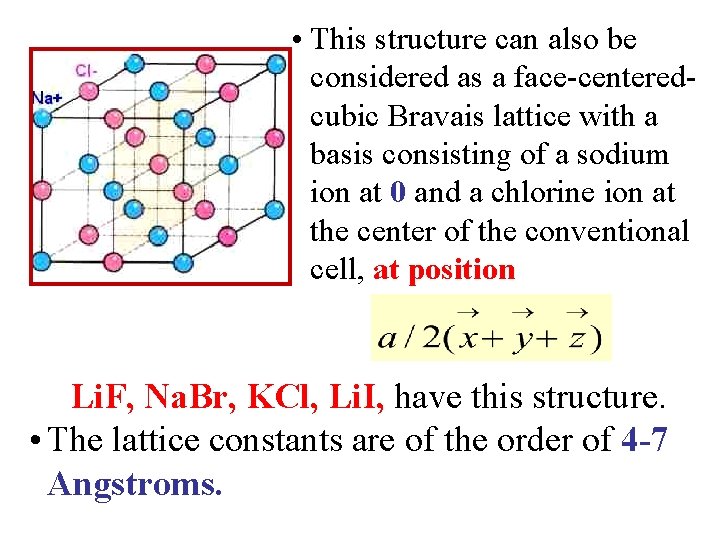
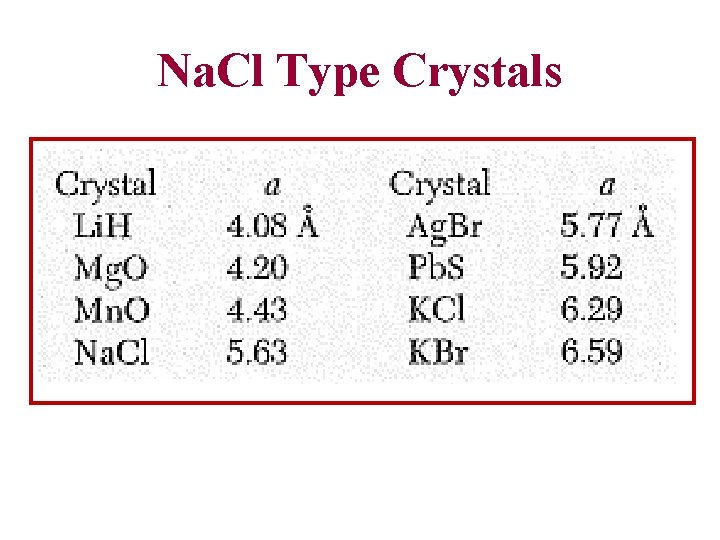
• This structure can also be considered as a face-centeredcubic Bravais lattice with a basis consisting of a sodium ion at 0 and a chlorine ion at the center of the conventional cell, at position Li. F, Na. Br, KCl, Li. I, have this structure. • The lattice constants are of the order of 4 -7 Angstroms.

Na. Cl Structure • Take the Na. Cl unit cell & remove all “red” Cl ions, leaving only the “blue” Na. Comparing this with the FCC unit cell, it is found to be that they are identical. So, the Na ions are on a FCC sublattice.

Na. Cl Type Crystals

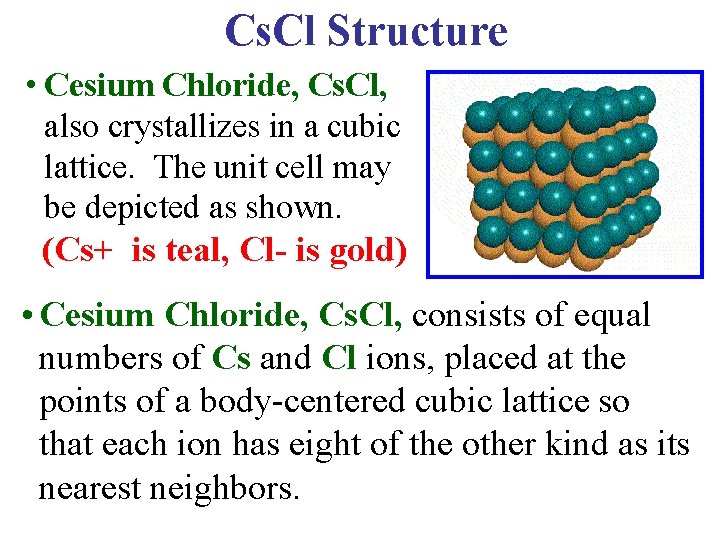
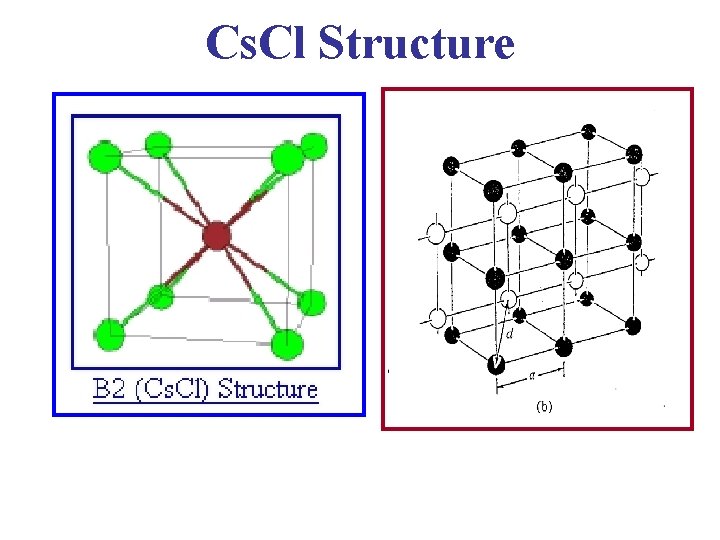
Cs. Cl Structure • Cesium Chloride, Cs. Cl, also crystallizes in a cubic lattice. The unit cell may be depicted as shown. (Cs+ is teal, Cl- is gold) • Cesium Chloride, Cs. Cl, consists of equal numbers of Cs and Cl ions, placed at the points of a body-centered cubic lattice so that each ion has eight of the other kind as its nearest neighbors.

Cs. Cl Structure

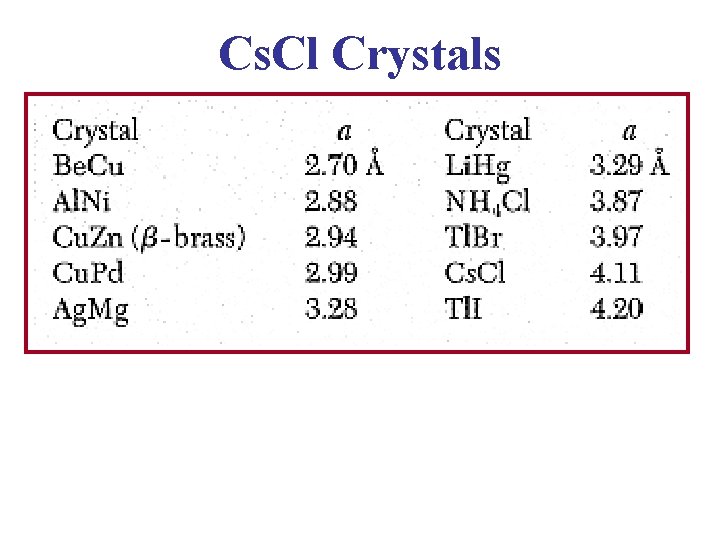
Cs. Cl Structure • The translational symmetry of this structure is that of the simple cubic Bravais lattice, and is described as a simple cubic lattice with a basis consisting of a Cs ion at the origin 0 and a Cl ion at the cube center: • Cs. Br & Cs. I crystallize in this structure. The lattice constants are of the order of 4 angstroms.

Cs. Cl Structure 8 cells

Cs. Cl Crystals

The Ancient “Periodic Table”

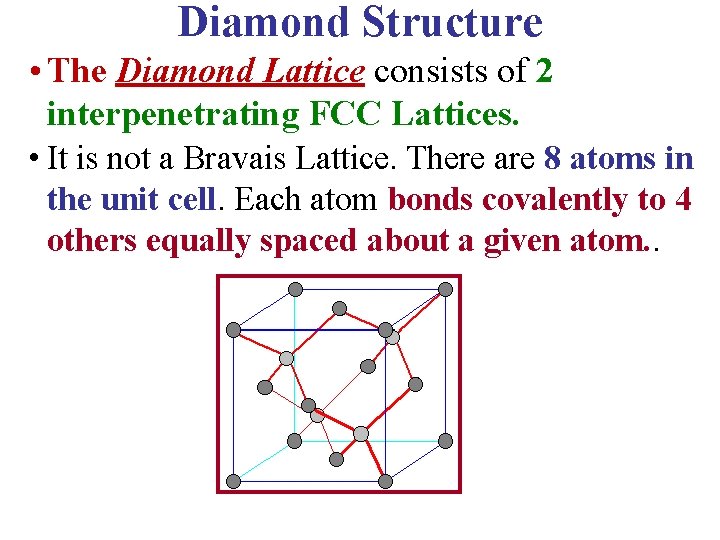
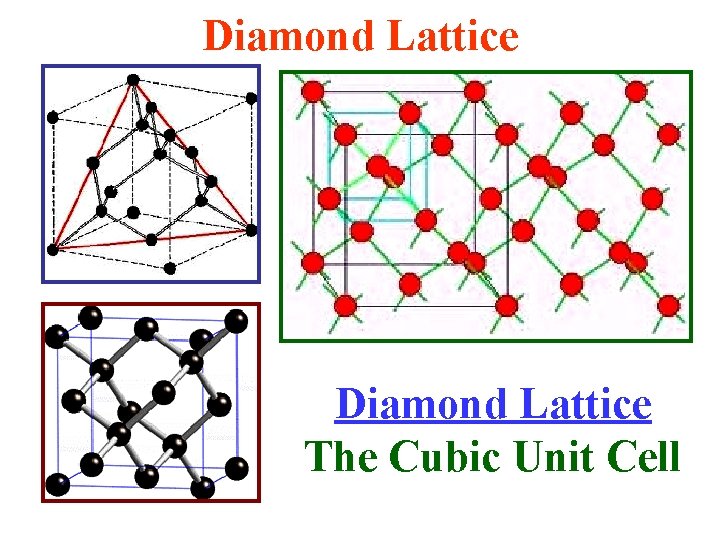
Diamond Structure • The Diamond Lattice consists of 2 interpenetrating FCC Lattices. • It is not a Bravais Lattice. There are 8 atoms in the unit cell. Each atom bonds covalently to 4 others equally spaced about a given atom. .

• The Diamond Lattice consists of 2 interpenetrating FCC Lattices. • The Coordination Number = 4. • The diamond lattice is not a Bravais lattice. C, Si, Ge & Sn crystallize in the Diamond structure.

Diamond Lattice The Cubic Unit Cell

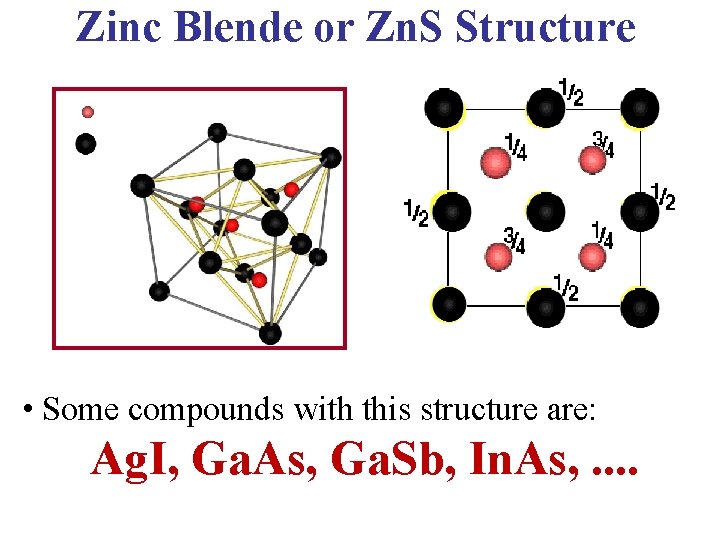
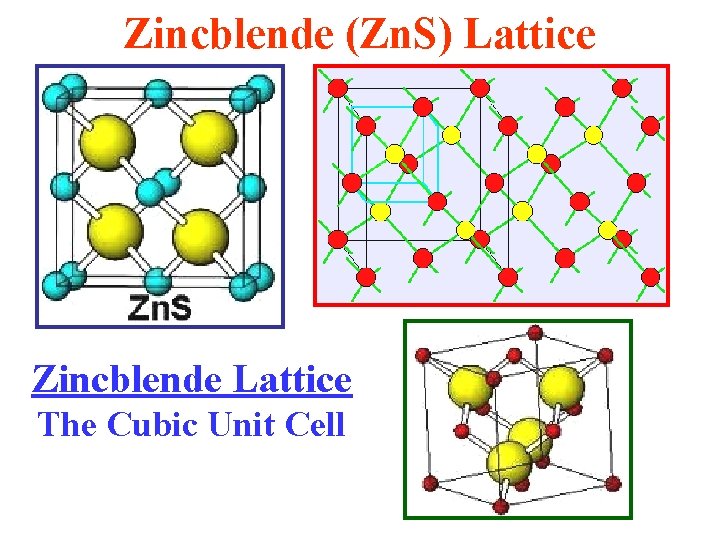
Zinc Blende or Zn. S Structure • The Zincblende Structure has equal numbers of zinc and sulfur ions distributed on a diamond lattice, so that Each has 4 of the opposite kind as nearest-neighbors. • This structure is an example of a lattice with a basis, both because of the geometrical position of the atoms & because two types of atoms occur.

Zinc Blende or Zn. S Structure • Some compounds with this structure are: Ag. I, Ga. As, Ga. Sb, In. As, . .

Zincblende (Zn. S) Lattice Zincblende Lattice The Cubic Unit Cell

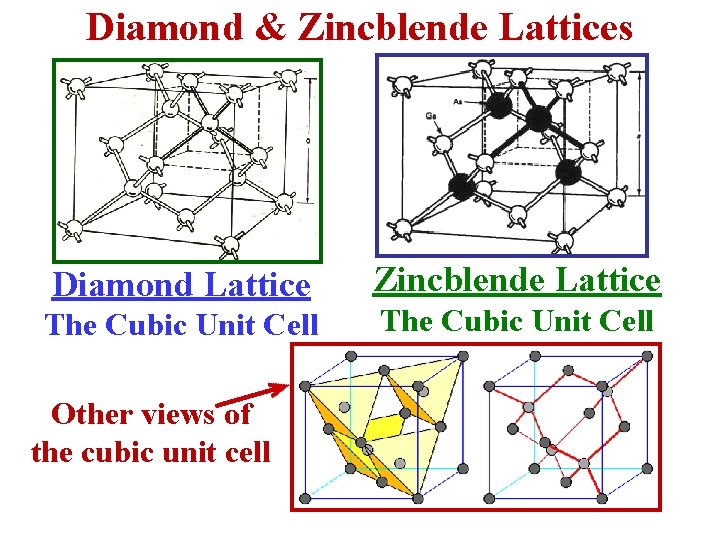
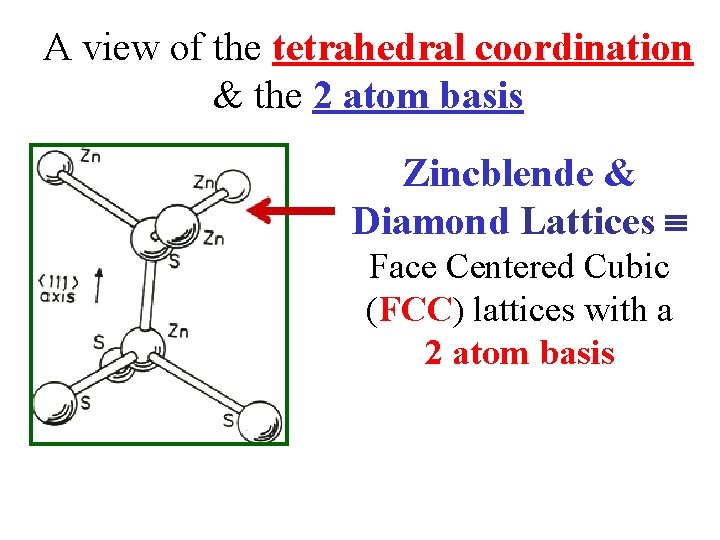
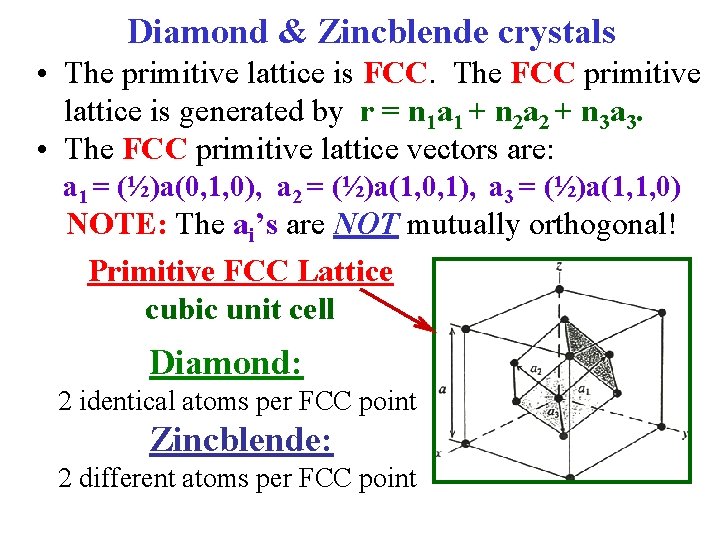
Diamond & Zincblende Structures A brief discussion of both of these structures & a comparison. • These two are technologically important structures because many common semiconductors have Diamond or Zincblende Crystal Structures • They obviously share the same geometry. • In both structures, the atoms are all tetrahedrally coordinated. That is, atom has 4 nearest-neighbors. • In both structures, the basis set consists of 2 atoms. In both structures, the primitive lattice Face Centered Cubic (FCC). • In both the Diamond & the Zincblende lattice there are 2 atoms per fcc lattice point. In Diamond: The 2 atoms are the same. In Zincblende: The 2 atoms are different.

Diamond & Zincblende Lattices Diamond Lattice The Cubic Unit Cell Other views of the cubic unit cell Zincblende Lattice The Cubic Unit Cell

A view of the tetrahedral coordination & the 2 atom basis Zincblende & Diamond Lattices Face Centered Cubic (FCC) lattices with a 2 atom basis

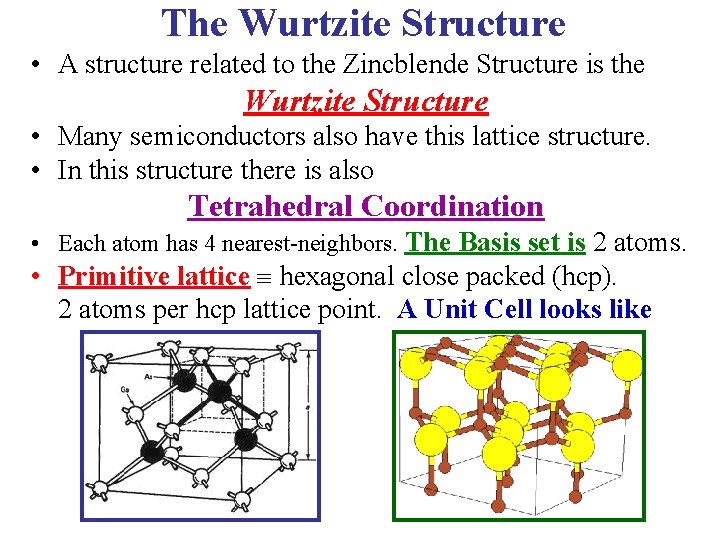
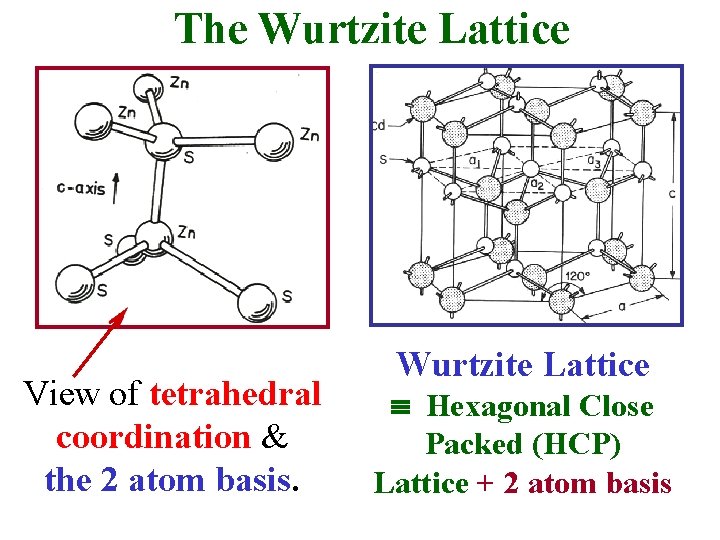
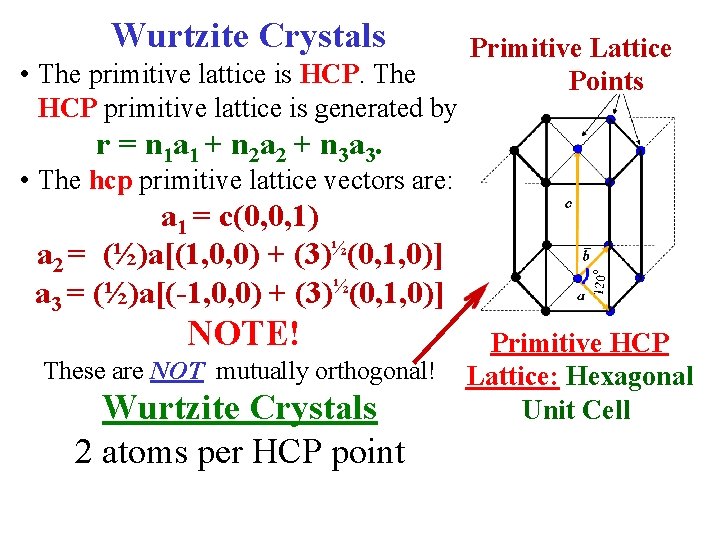
The Wurtzite Structure • A structure related to the Zincblende Structure is the Wurtzite Structure • Many semiconductors also have this lattice structure. • In this structure there is also Tetrahedral Coordination • Each atom has 4 nearest-neighbors. The Basis set is 2 atoms. • Primitive lattice hexagonal close packed (hcp). 2 atoms per hcp lattice point. A Unit Cell looks like

The Wurtzite Lattice View of tetrahedral coordination & the 2 atom basis. Wurtzite Lattice Hexagonal Close Packed (HCP) Lattice + 2 atom basis

Diamond & Zincblende crystals • The primitive lattice is FCC. The FCC primitive lattice is generated by r = n 1 a 1 + n 2 a 2 + n 3 a 3. • The FCC primitive lattice vectors are: a 1 = (½)a(0, 1, 0), a 2 = (½)a(1, 0, 1), a 3 = (½)a(1, 1, 0) NOTE: The ai’s are NOT mutually orthogonal! Primitive FCC Lattice cubic unit cell Diamond: 2 identical atoms per FCC point Zincblende: 2 different atoms per FCC point

Wurtzite Crystals Primitive Lattice Points • The primitive lattice is HCP. The HCP primitive lattice is generated by r = n 1 a 1 + n 2 a 2 + n 3 a 3. • The hcp primitive lattice vectors are: a 1 = c(0, 0, 1) a 2 = (½)a[(1, 0, 0) + (3)½(0, 1, 0)] a 3 = (½)a[(-1, 0, 0) + (3)½(0, 1, 0)] NOTE! These are NOT mutually orthogonal! Wurtzite Crystals 2 atoms per HCP point Primitive HCP Lattice: Hexagonal Unit Cell

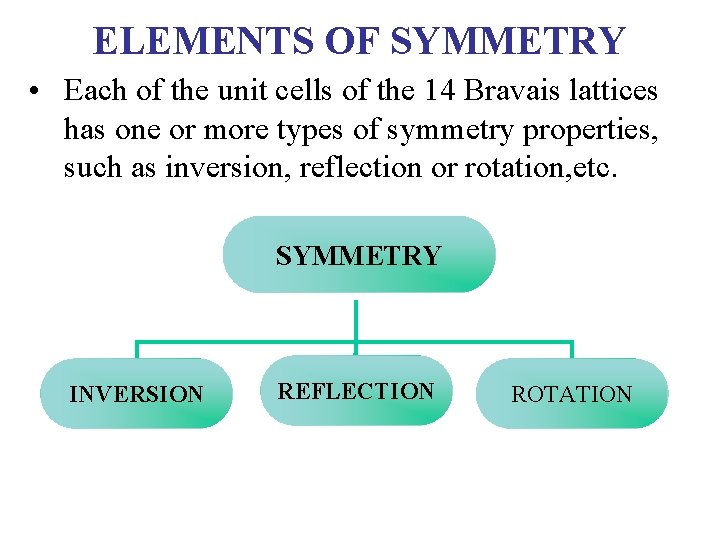
ELEMENTS OF SYMMETRY • Each of the unit cells of the 14 Bravais lattices has one or more types of symmetry properties, such as inversion, reflection or rotation, etc. SYMMETRY INVERSION REFLECTION ROTATION

Typical symmetry properties of a lattice. Some types of operations that can leave a lattice invariant. Operation Element Inversion Point Reflection Plane Rotation Axis Rotoinversion Axes

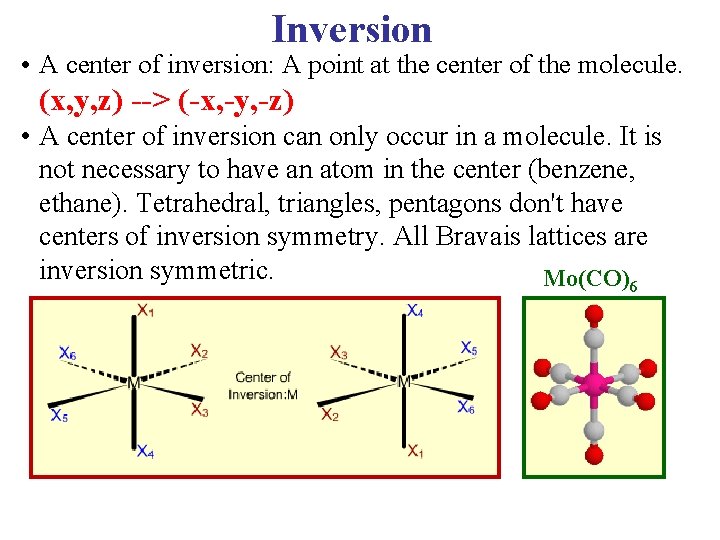
Inversion • A center of inversion: A point at the center of the molecule. (x, y, z) --> (-x, -y, -z) • A center of inversion can only occur in a molecule. It is not necessary to have an atom in the center (benzene, ethane). Tetrahedral, triangles, pentagons don't have centers of inversion symmetry. All Bravais lattices are inversion symmetric. Mo(CO)6

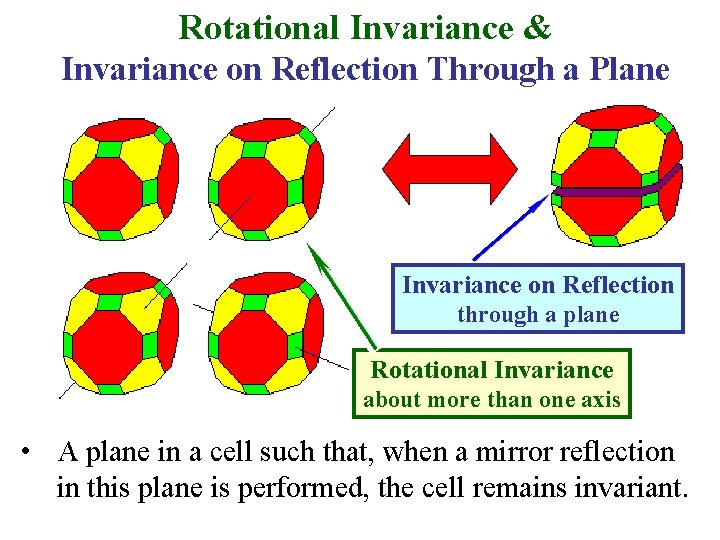
Rotational Invariance & Invariance on Reflection Through a Plane Invariance on Reflection through a plane Rotational Invariance about more than one axis • A plane in a cell such that, when a mirror reflection in this plane is performed, the cell remains invariant.

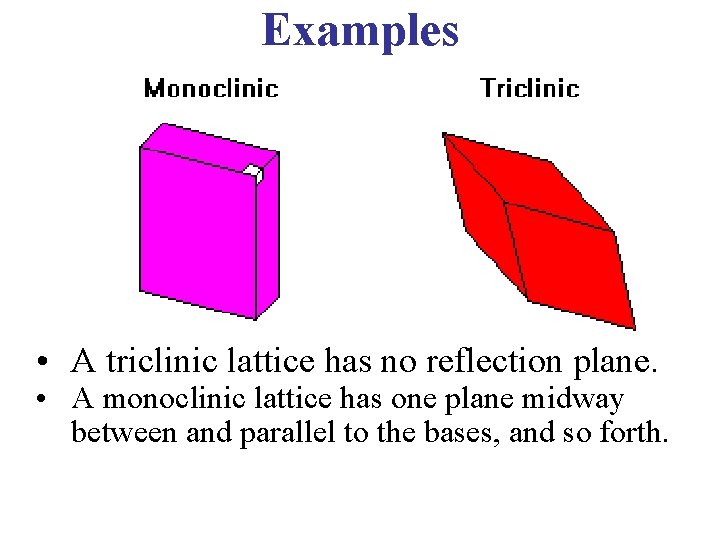
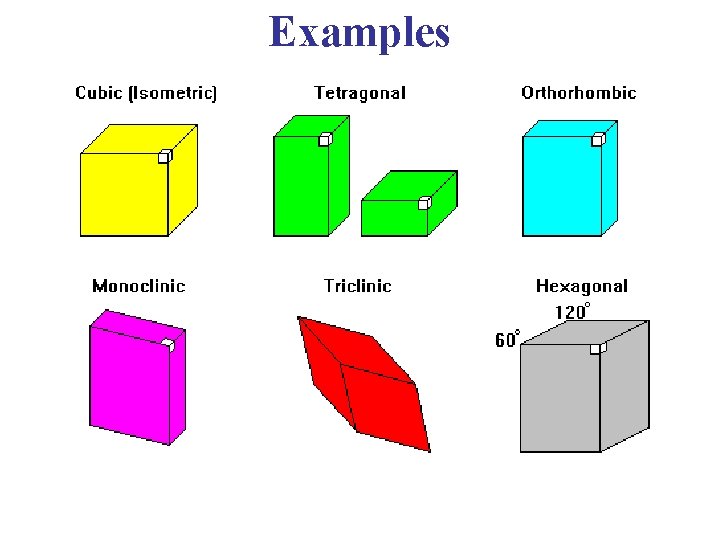
Examples • A triclinic lattice has no reflection plane. • A monoclinic lattice has one plane midway between and parallel to the bases, and so forth.

Rotational Symmetry • There always a finite number of rotational symmetries for a lattice. • A single molecule can have any degree of rotational symmetry, but an infinite periodic lattice – can not.

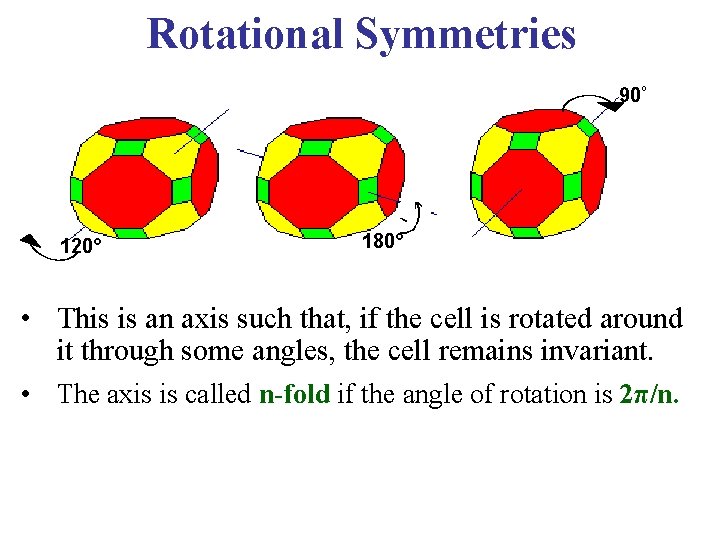
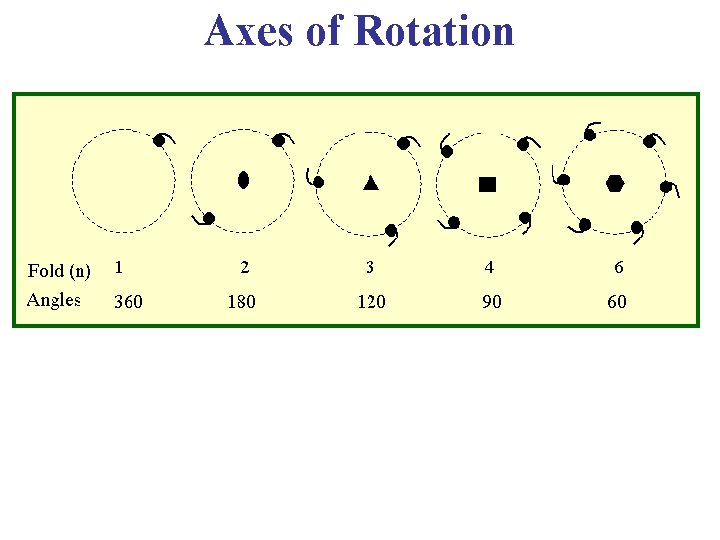
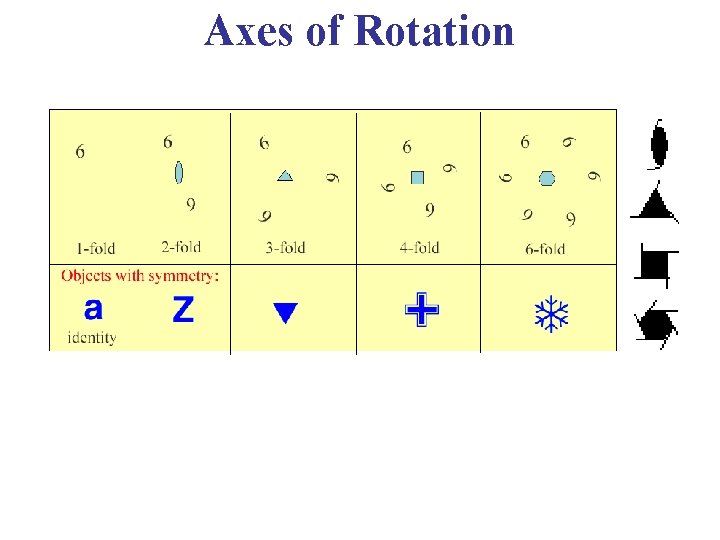
Rotational Symmetries 90º 120° 180° • This is an axis such that, if the cell is rotated around it through some angles, the cell remains invariant. • The axis is called n-fold if the angle of rotation is 2π/n.

Axes of Rotation

Axes of Rotation

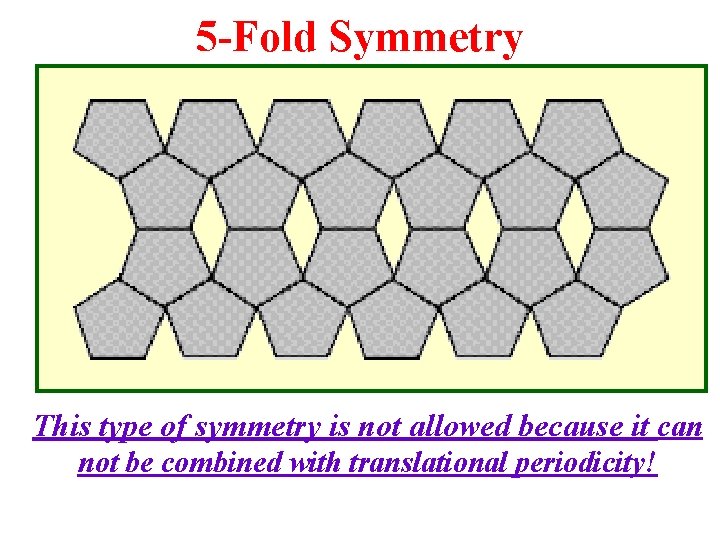
5 -Fold Symmetry This type of symmetry is not allowed because it can not be combined with translational periodicity!

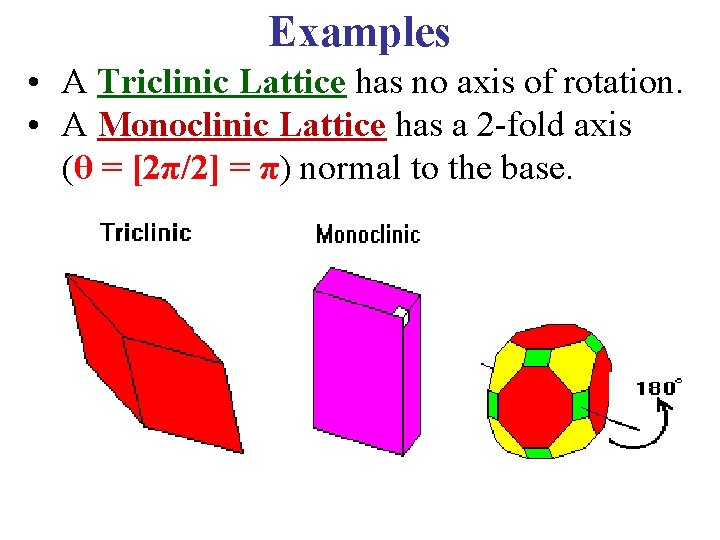
Examples • A Triclinic Lattice has no axis of rotation. • A Monoclinic Lattice has a 2 -fold axis (θ = [2π/2] = π) normal to the base. 90°

Examples