Outline 2 1 Fundamental Concepts of Atom and

Outline 2. 1 Fundamental Concepts of Atom and Bonding 2. 2 The Periodic Table General Chemistry 2. 3 Bonding Forces and Energies 2. 4 Primary Inter-atomic Bonds 2. 5 โครงสรางผลก (Crystal Structures) 2. 6ระบบผลก (Crystal systems) 2. 7 ผลกของโลหะ (Metallic Crystal Structures) 2. 8 ทศทางของผลก (Crystallographic Directions) 2. 9 ระนาบผลก (Crystallographic planes) 2. 10 ความหนาแนน (Density Computations) 3

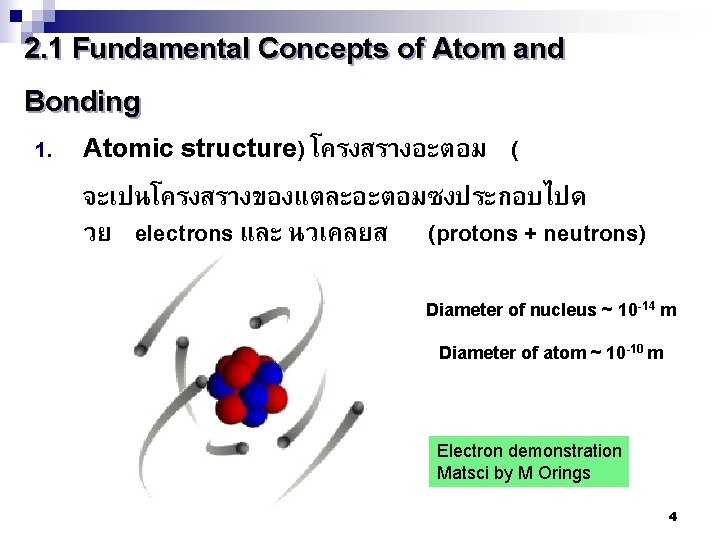
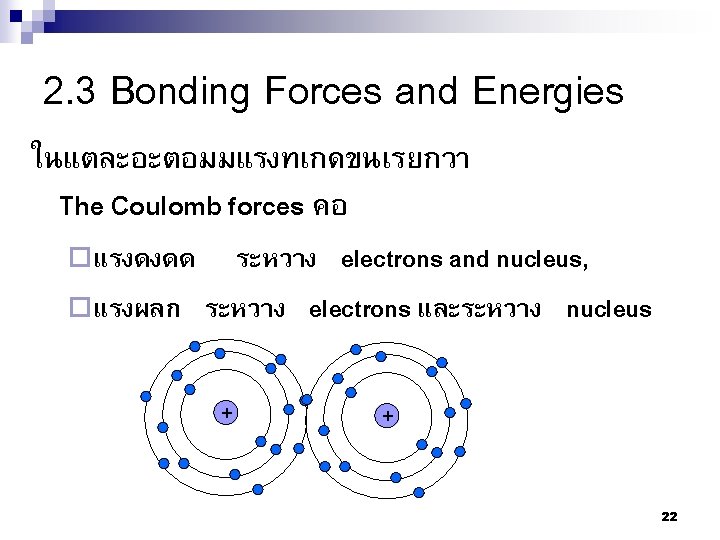
2. 1 Fundamental Concepts of Atom and Bonding 1. Atomic structure) โครงสรางอะตอม ( จะเปนโครงสรางของแตละอะตอมซงประกอบไปด วย electrons และ นวเคลยส (protons + neutrons) Diameter of nucleus ~ 10 -14 m Diameter of atom ~ 10 -10 m Electron demonstration Matsci by M Orings 4

n ตวอยาง 2 Calculate the number of atoms per cm 3(n) of carbon with a density, d = 1. 8 g/cm 3, M =12 amu n (Carbon) = 1. 8 g/cm 3 6. 023 1023 atoms/mol = 9 1022 C/cm 3 12 g/mol For a molecular solid like ice, one uses the molecular mass, M (H 2 O) = 18. With a density of 1 g/cm 3, n (H 2 O) = 1 g/cm 3 6. 023 1023 atoms/mol = 3. 3 1022 H 2 O/cm 3 18 g/mol Note that since the water molecule contains 3 atoms, this is equivalent to 9. 9 1022 atoms/cm 3. 11

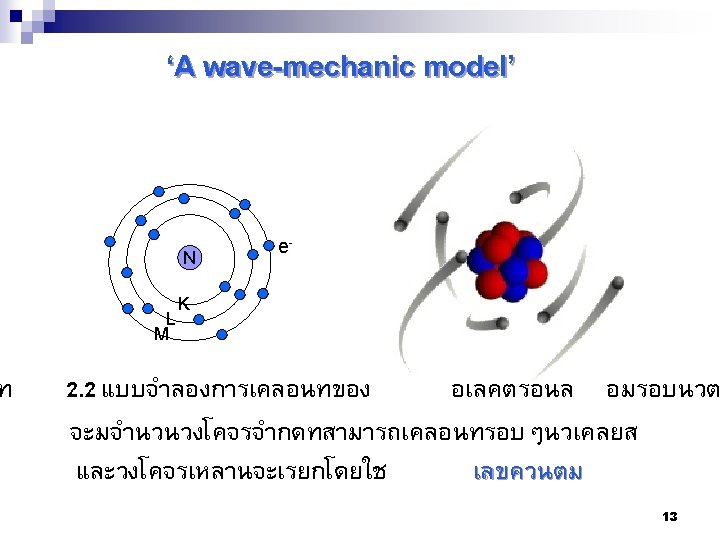
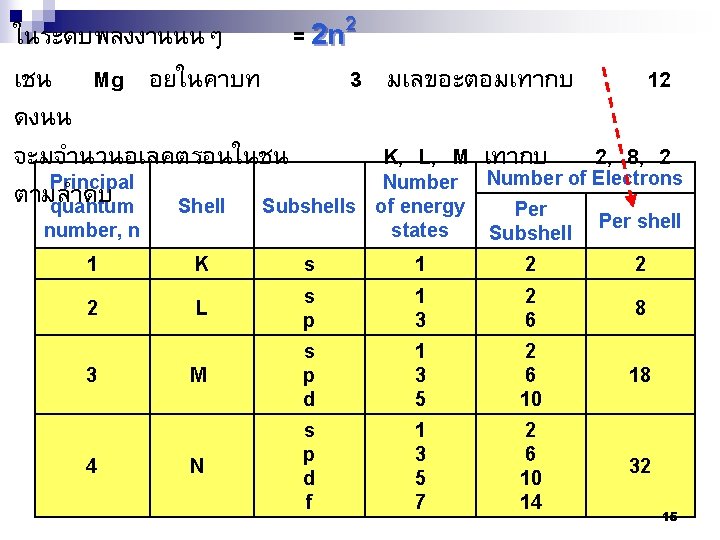
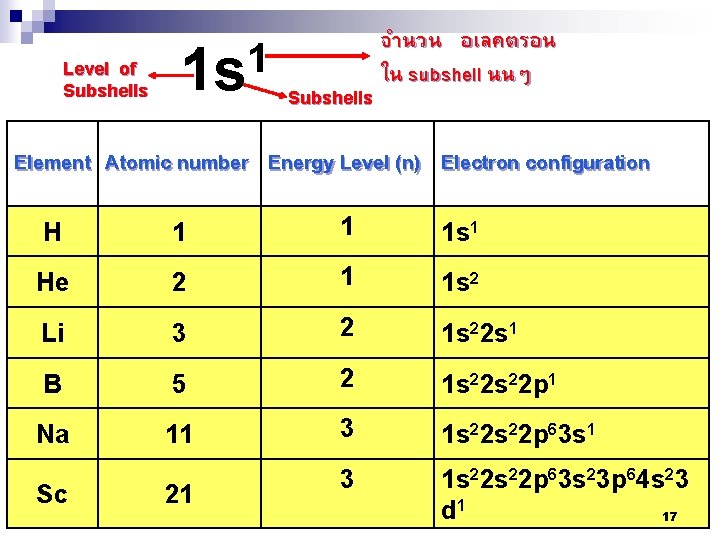
ในระดบพลงงานนนๆ = 2 n 2 เชน Mg อยในคาบท 3 มเลขอะตอมเทากบ 12 ดงนน จะมจำนวนอเลคตรอนในชน K, L, M เทากบ 2, 8, 2 Principal Number of Electrons ตามลำดบ quantum Shell Subshells of energy Per number, n states Subshell Per shell 1 K s 1 2 2 2 L s p 1 3 2 6 8 M s p d 1 3 5 2 6 10 18 N s p d f 1 3 5 7 2 6 10 14 32 3 4 15

Level of Subshells 1 1 s Subshells จำนวน อเลคตรอน ใน subshell นนๆ Element Atomic number Energy Level (n) Electron configuration H 1 1 1 s 1 He 2 1 1 s 2 Li 3 2 1 s 22 s 1 B 5 2 1 s 22 p 1 Na 11 3 1 s 22 s 22 p 63 s 23 p 64 s 23 d 1 17 Sc 21

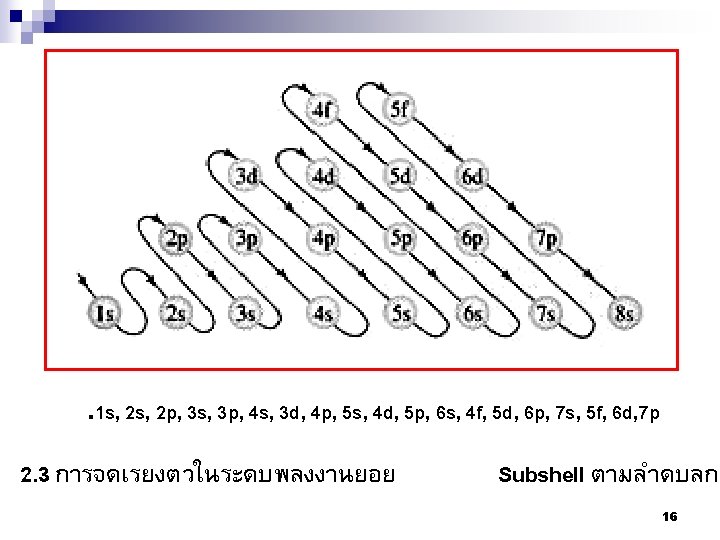
แบบฝกหด n ���� Electron configuration ของธาตตอไปน ¨N atomic number = 7 (1 s 2 s 2 p ) ¨Mg atomic number = 12 (1 s 2 s 2 p 3 s ) ¨Fe atomic number = 26 2 2 2 3 2 6 2 1 s 22 p 63 s 23 p 64 s 23 d 6 . 1 s, 2 p, 3 s, 3 p, 4 s, 3 d, 4 p, 5 s, 4 d, 5 p, 6 s, 4 f, 5 d, 6 p, 7 s, 5 f, 6 d, 7 p 18

¨Mo atomic number = 42 1 s 22 p 63 s 23 p 64 s 23 d 104 p 6 5 s 2 4 d 4 but the s electron can move to make a halffull orbital, therefore 1 s 22 p 63 s 23 p 64 s 23 d 104 p 6 5 s 1 4 d 5 Or 1 s 22 p 63 s 23 p 63 d 104 s 24 p 6 4 d 55 s 1 . 1 s, 2 p, 3 s, 3 p, 4 s, 3 d, 4 p, 5 s, 4 d, 5 p, 6 s, 4 f, 5 d, 6 p, 7 s, 5 f, 6 d, 7 p 19

20

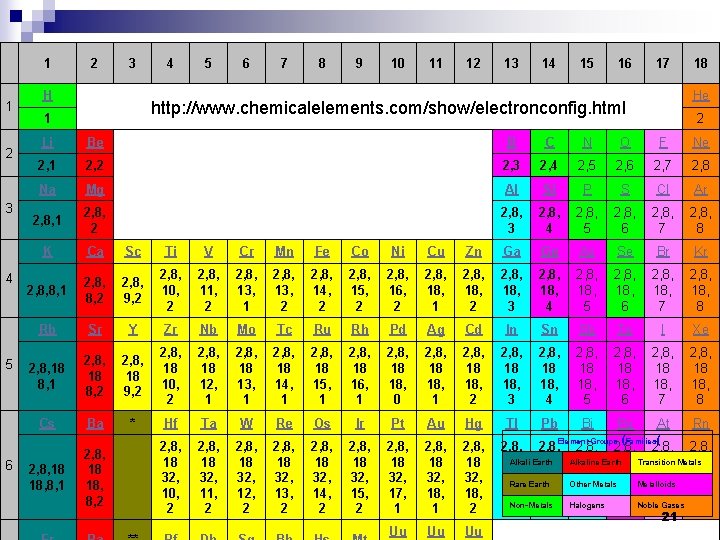
1 2 3 4 5 6 1 2 3 H 4 5 6 7 8 9 10 11 12 13 14 15 16 17 He http: //www. chemicalelements. com/show/electronconfig. html 1 18 2 Li Be B C N O F Ne 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 Na Mg Al Si P S Cl Ar 2, 8, 1 2, 8, 2 2, 8, 3 2, 8, 4 2, 8, 5 2, 8, 6 2, 8, 7 2, 8, 8 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 2, 8, 8, 1 2, 8, 8, 2 2, 8, 9, 2 2, 8, 10, 2 2, 8, 11, 2 2, 8, 13, 1 2, 8, 13, 2 2, 8, 14, 2 2, 8, 15, 2 2, 8, 16, 2 2, 8, 18, 2 2, 8, 18, 3 2, 8, 18, 4 2, 8, 18, 5 2, 8, 18, 6 2, 8, 18, 7 2, 8, 18, 8 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 2, 8, 18 8, 1 2, 8, 18 8, 2 2, 8, 18 9, 2 2, 8, 18 10, 2 2, 8, 18 12, 1 2, 8, 18 13, 1 2, 8, 18 14, 1 2, 8, 18 15, 1 2, 8, 18 16, 1 2, 8, 18 18, 0 2, 8, 18 18, 1 2, 8, 18 18, 2 2, 8, 18 18, 3 2, 8, 18 18, 4 2, 8, 18 18, 5 2, 8, 18 18, 6 2, 8, 18 18, 7 2, 8, 18 18, 8 Cs Ba * Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 2, 8, 18 32, 10, 2 2, 8, 18 32, 11, 2 2, 8, 18 32, 12, 2 2, 8, 18 32, 13, 2 2, 8, 18 32, 14, 2 2, 8, 18 32, 15, 2 2, 8, 18 32, 17, 1 2, 8, 18 32, 18, 2 Uu Uu Uu 2, 8, 18 18, 8, 1 2, 8, 18 18, 8, 2 Element Groups (Families( 2, 8, 2, 8, Alkali Earth 18 18 Alkaline 18 Earth 18 Transition 18 Metals 18 32, Other 32, Metals 32, Metalloids 32, Rare Earth 18, 18, 18, Non-Metals Halogens Noble Gases 3 4 5 6 7 8 21

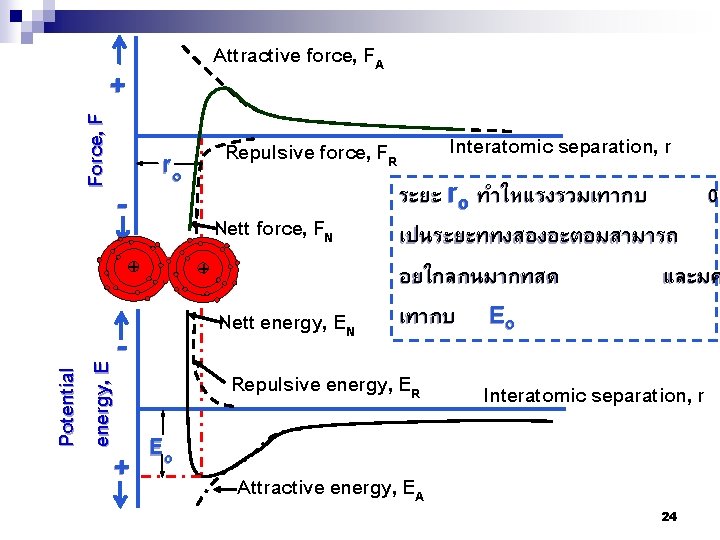
Attractive force, FA Force, F + ro - Nett force, FN + + Nett energy, EN Potential energy, E - + Interatomic separation, r Repulsive force, FR ระยะ ro ทำใหแรงรวมเทากบ 0 เปนระยะททงสองอะตอมสามารถ อยใกลกนมากทสด และมค เทากบ Eo Repulsive energy, ER Eo Attractive energy, EA Interatomic separation, r 24

Figure 4. An atomic resolution TEM image of Si/Tb. Si 2/Si heterostructure with simulated images pasted for direct comparison. www. tms. org/pubs/journals/JOM/0509/fig 4. large. gif 27

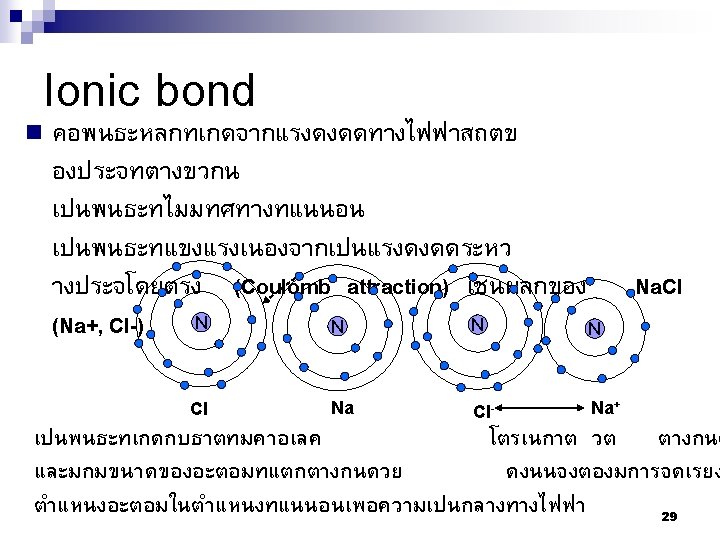
2. 4 Primary Interatomic Bonds 1. 2. 3. Ionic Bond Covalent Bond Metallic Bond 28

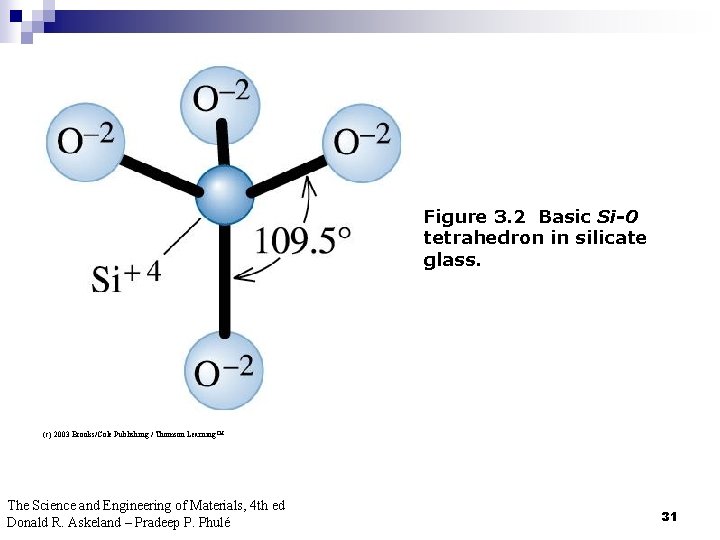
Figure 3. 2 Basic Si-0 tetrahedron in silicate glass. (c) 2003 Brooks/Cole Publishing / Thomson Learning™ The Science and Engineering of Materials, 4 th ed Donald R. Askeland – Pradeep P. Phulé 31

49

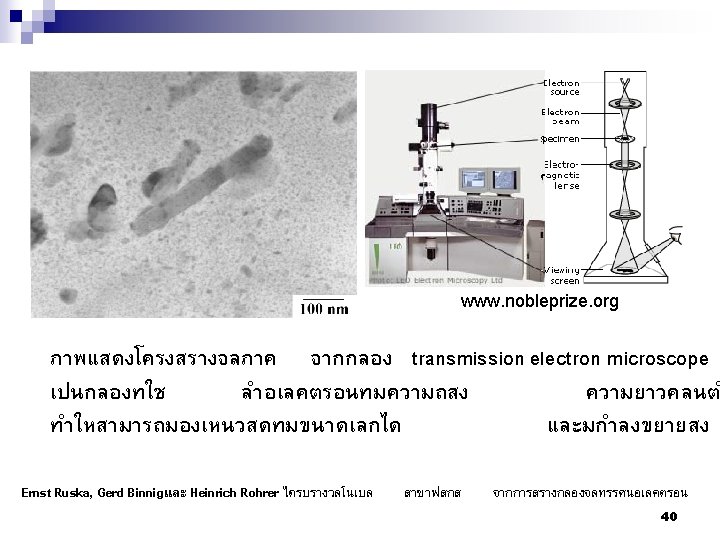
Summary Nuclei Nucleus Lattices Crystals (Grains) Crystalline Solid เกรน 5 mm ขอบเกรน 50

(a) Photograph of a silicon single crystal. (b) Micrograph of a polycrystalline stainless steel showing grains and grain boundaries (Courtesy Dr. M. Hua, Dr. I. Garcia, and Dr. A. J. Deardo. ) The Science and Engineering of Materials, 4 th ed Donald R. Askeland – Pradeep P. Phulé 51

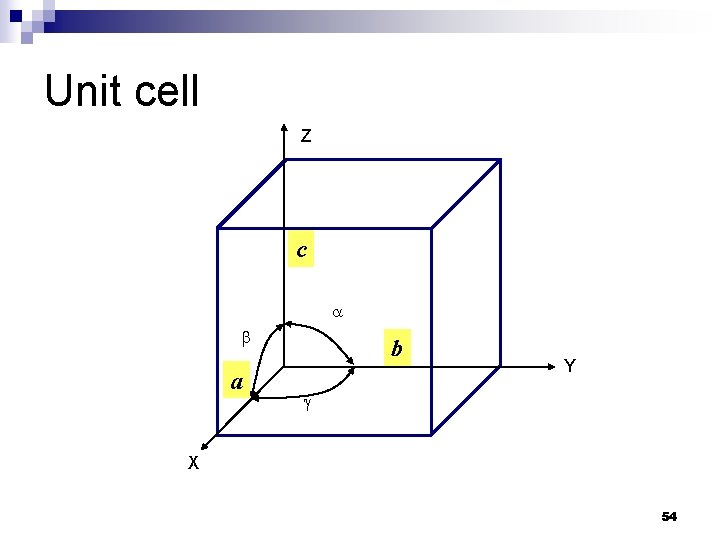
Unit cell Z c a b Y X 54

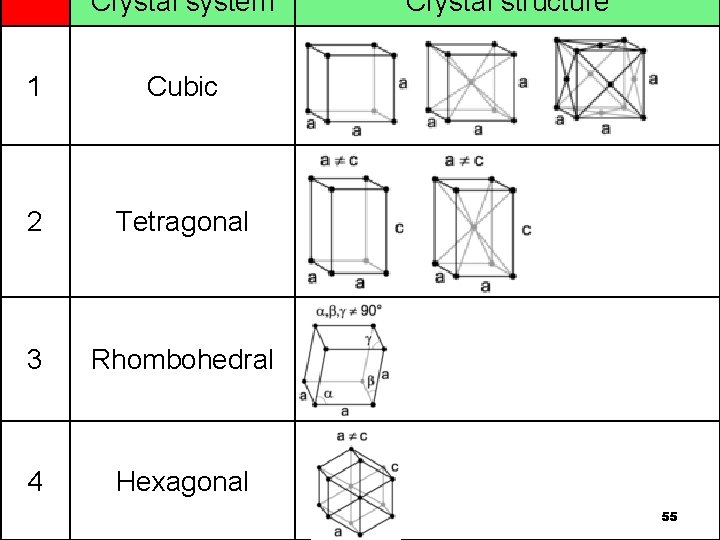
Crystal system 1 Cubic 2 Tetragonal 3 Rhombohedral 4 Hexagonal Crystal structure 55

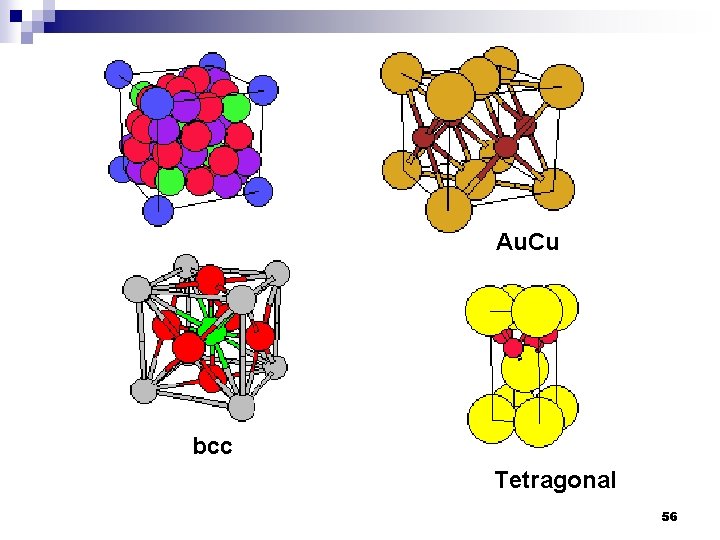
Au. Cu bcc Tetragonal 56

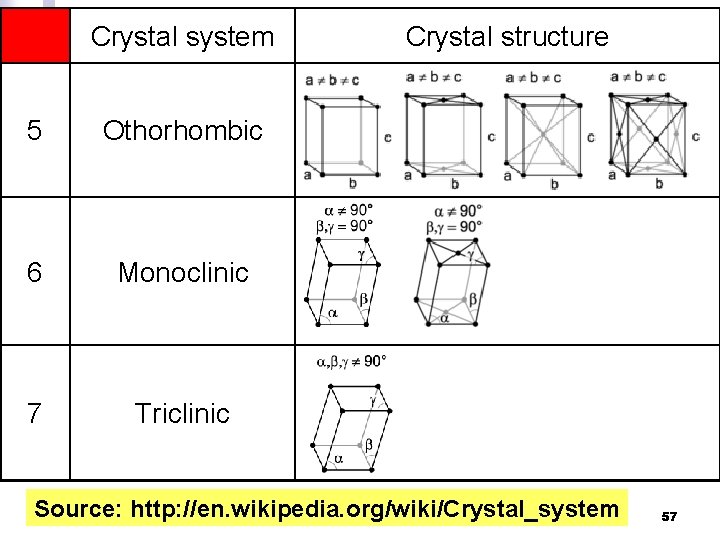
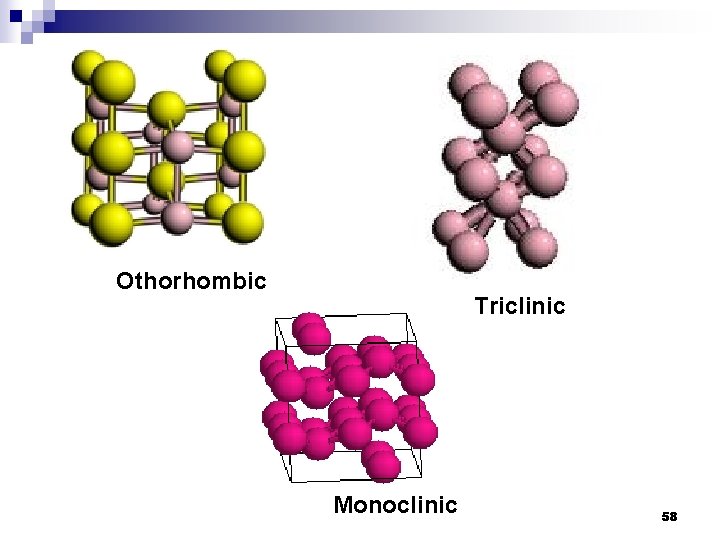
Crystal system 5 Othorhombic 6 Monoclinic 7 Triclinic Crystal structure Source: http: //en. wikipedia. org/wiki/Crystal_system 57

Othorhombic Triclinic Monoclinic 58

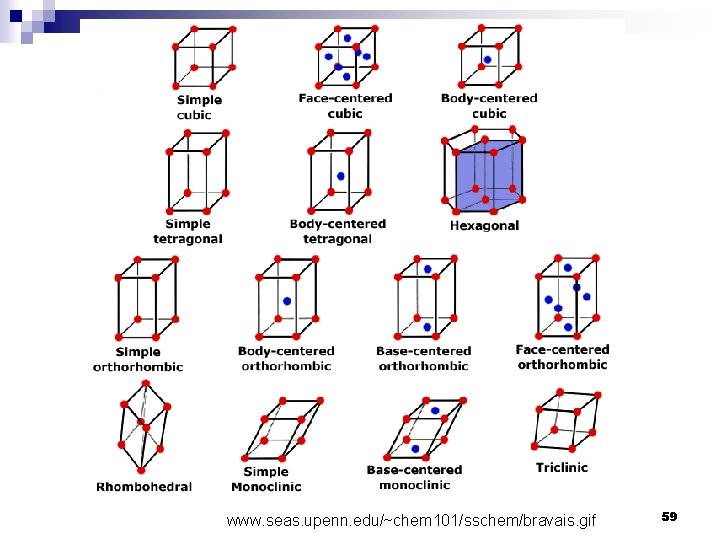
www. seas. upenn. edu/~chem 101/sschem/bravais. gif 59

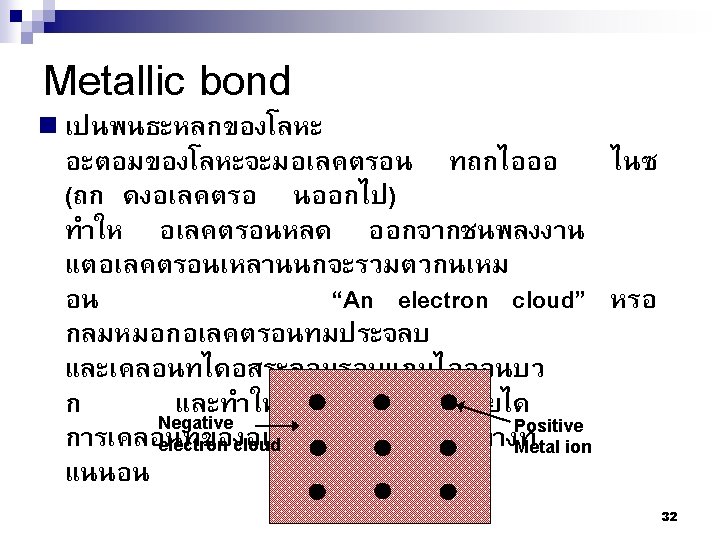
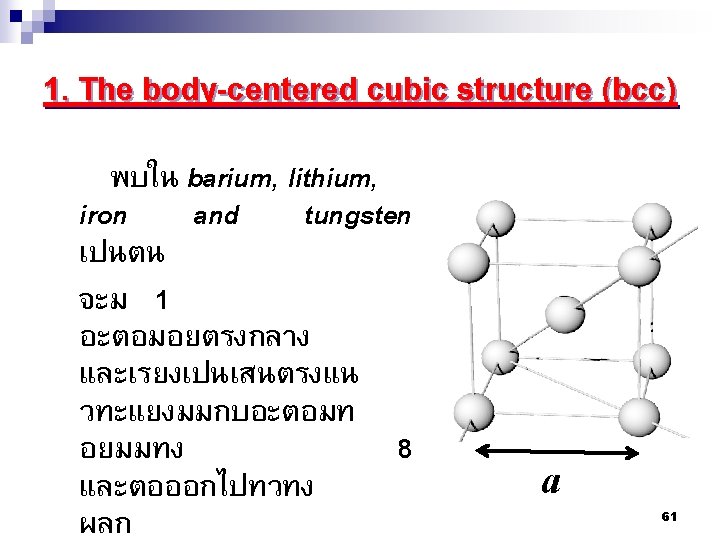
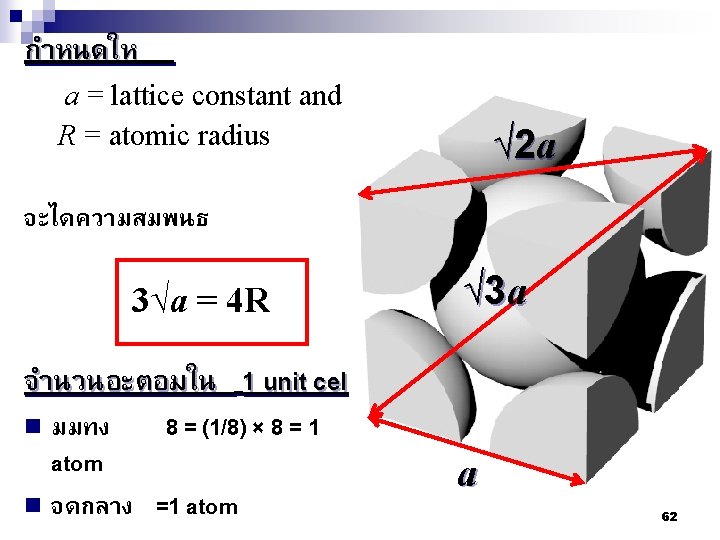
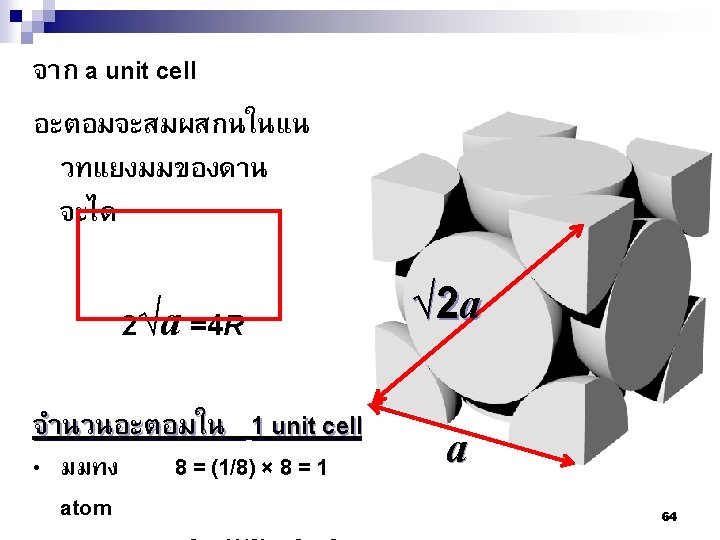
2. 7 โครงสรางผลกของโลหะ Metallic Crystal Structure There are 3 common crystal structures of metals 1. Body centered cubic structure-BCC 2. Face centered cubic structure-FCC 3. Hexagonal closed packed structure HCP 60

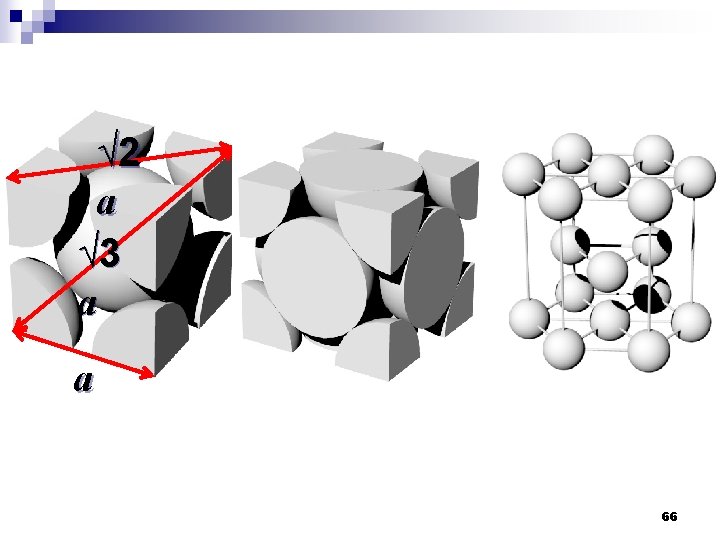
√ 2 a √ 3 a a 66

Atomic packing factor (APF) n If the atoms in a unit cell considered as a spherical therefore, APF = Volume of atoms in unit cell Volume of unit cell n In bcc, APF = 0. 68 n In fcc and hcp, APF = 0. 74 67

แบบฝกหด Calculate the lattice constant (a) for BCC structure of the iron unit cell with atomic radius R=0. 124 nm n Lead has a FCC crystal structure, an atomic radius of 0. 175 nm. Compute the volume of Lead atoms in a unit cell n 68

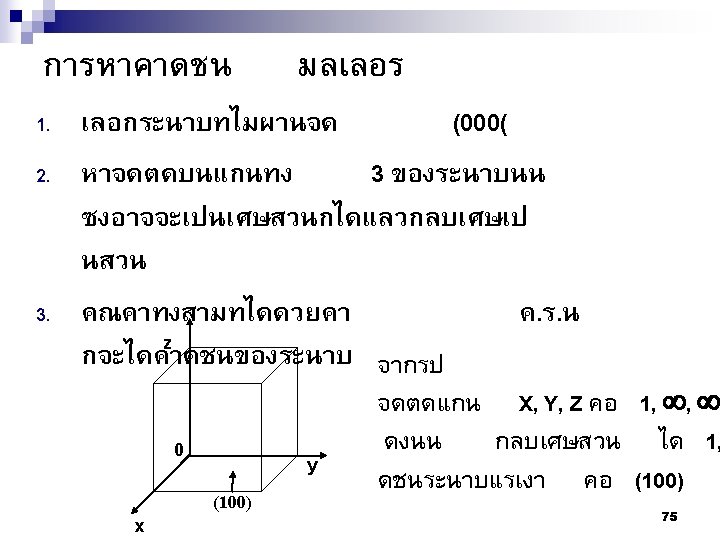
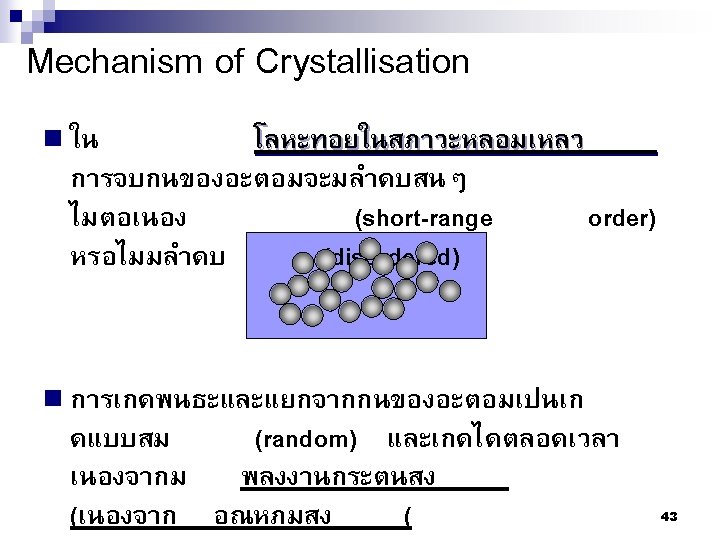
Z [001] [111] 000 X Y [010] [100] 70

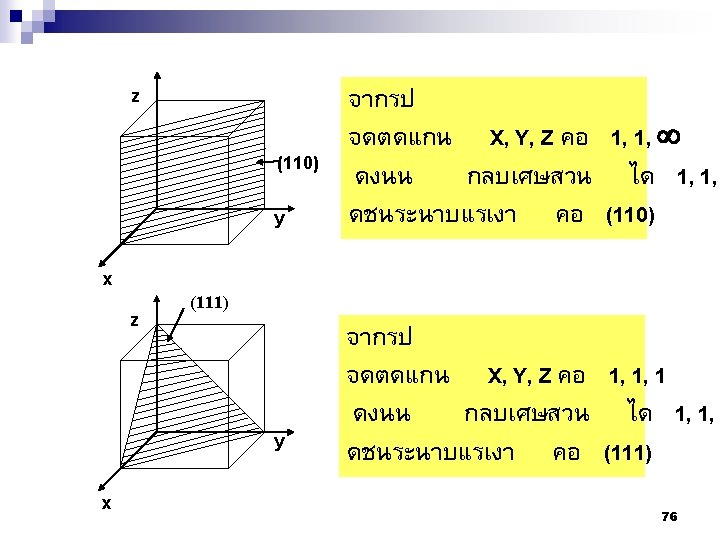
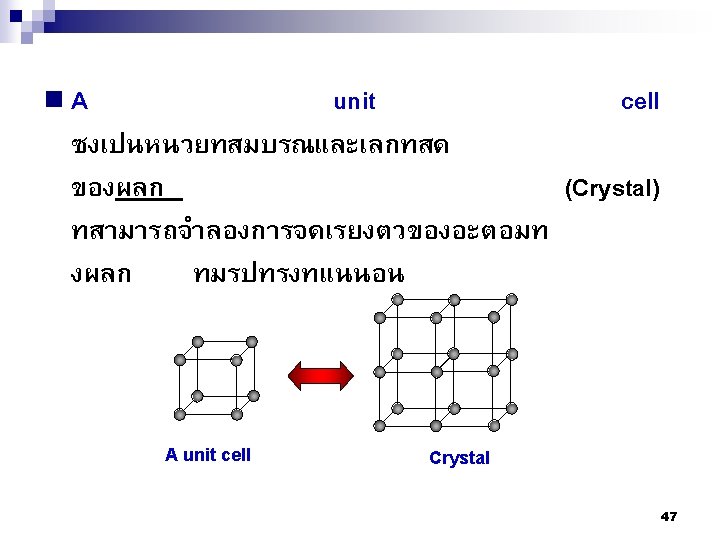
z h d c f 0 g 1/2 e x a gh = [011] oa = [100] cd=fh = [100] ob = [110] oe = [120] y oc = [111] of = [101] b oe ������ X Y Z ��� ½ , 1, 0 × 2 ����������� [120] 72

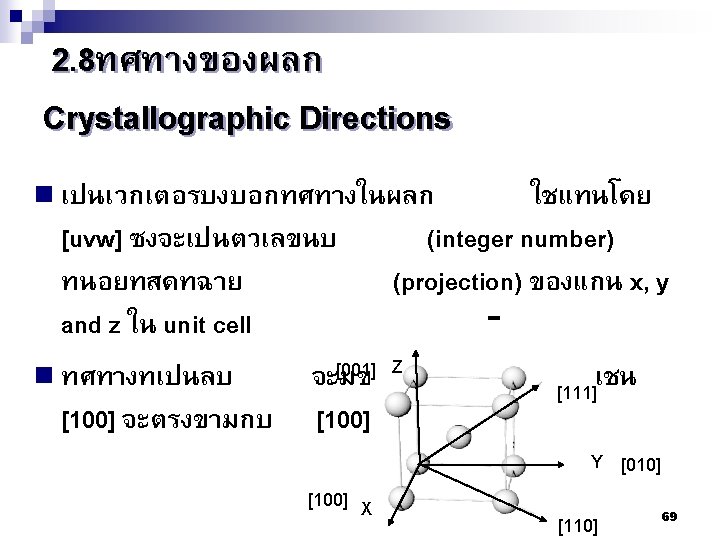
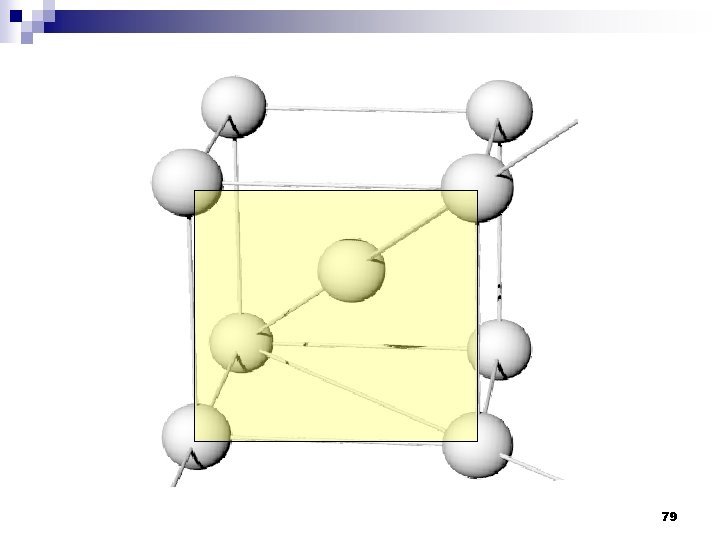
2. 9ระนาบผลก Crystallographic planes n Miller* indices is ‘ the reciprocals (สวนกลบ ) of the fractional intercepts (เศษสวนของสวนตด ) which the plane makes with the crystallographic x, y and z axes of the three nonparallel edges of the cubic unit cell’ n For cubic plane ใชสญลกษณ * William Hallowes Miller (1801 -1880) axes (hkl) for x, y and z 74

79

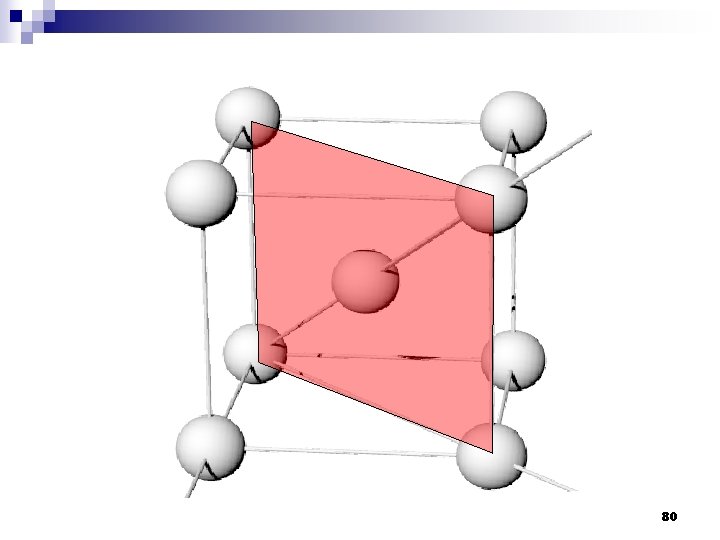
80

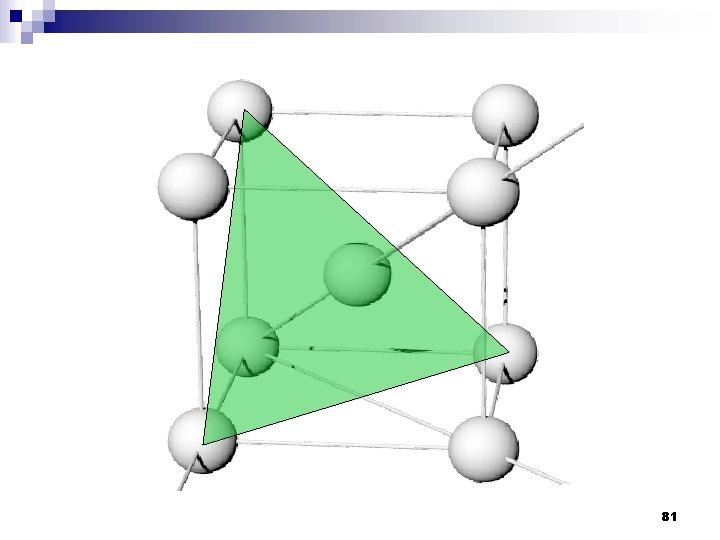
81

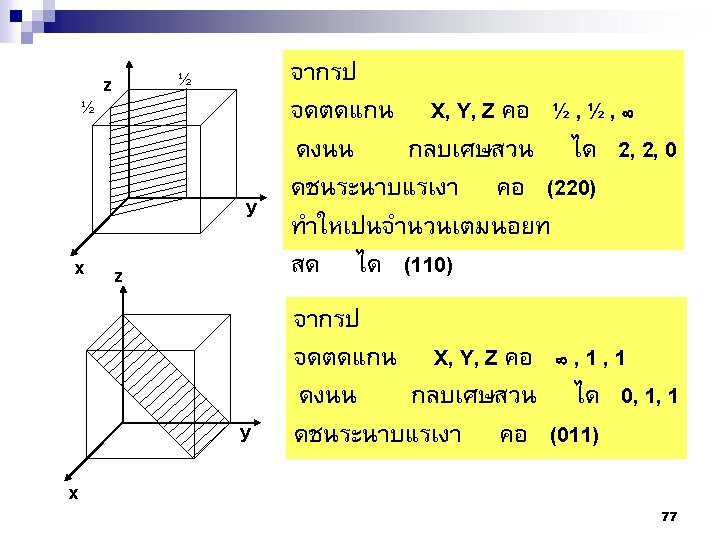
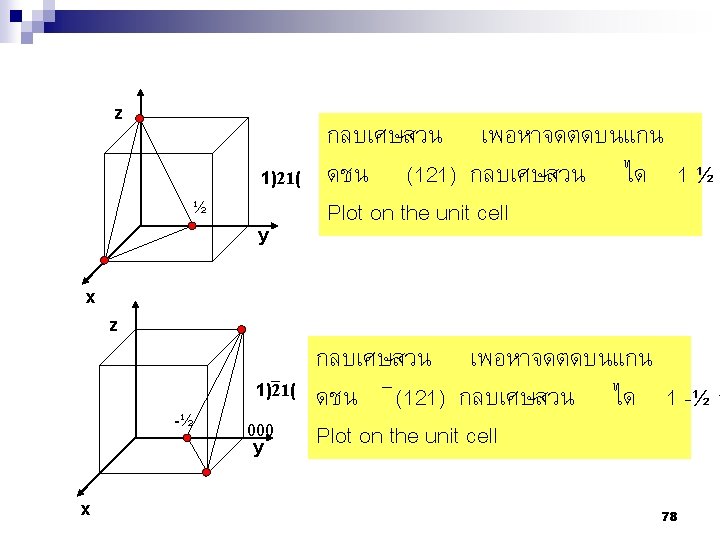
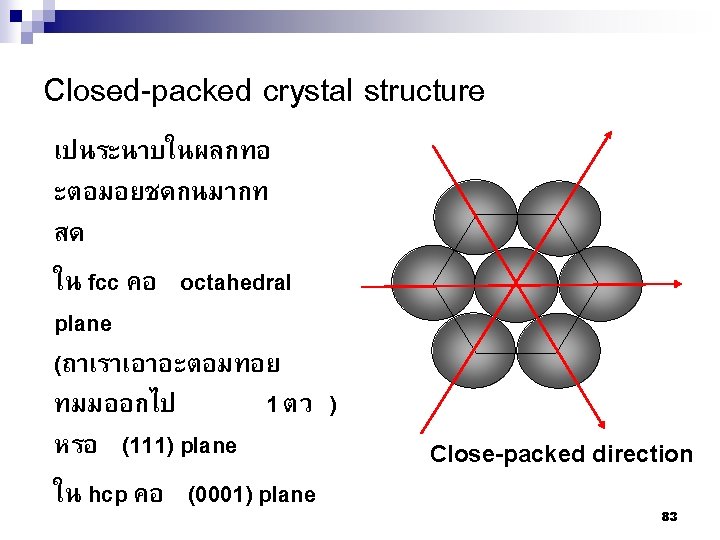
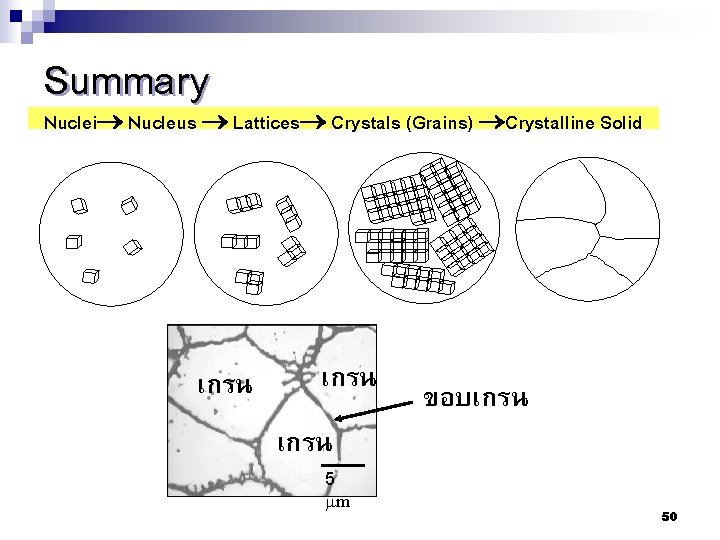
For hexagonal plane indices called Miller-Bravais indices n Direction ใชแทนโดย [uvtw], t=-(u+v) n Plane ใชแทนโดย (hkil), i=-(h+k) c (0001) a 3 a 2 a 1 82

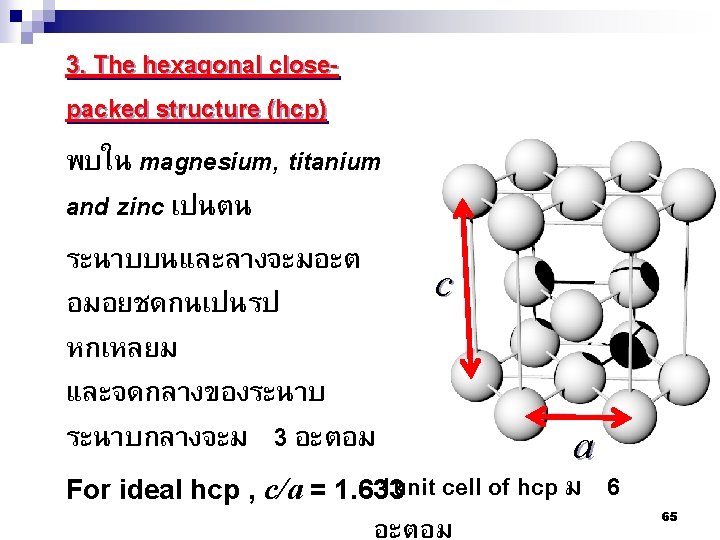
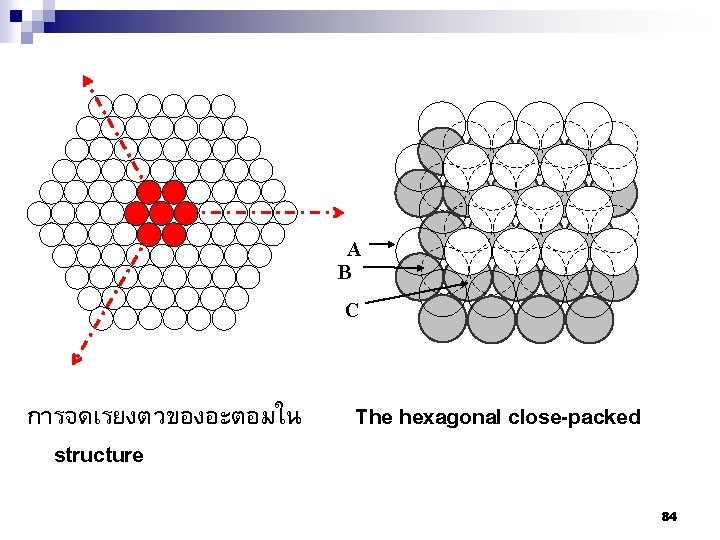
A B C การจดเรยงตวของอะตอมใน structure The hexagonal close-packed 84

n= จำนวนอะตอมใน 1 unit cell A= มวลอะตอม (amu) VC = the volume of the cell NA= the Avogadro number = 6. 023 1023 atoms/mol 86

Example Determining the Density of BCC Iron Determine the density of BCC iron, which has a lattice parameter of 0. 2866 nm. Example 3. 4 SOLUTION Atoms/cell = 2, a 0 = 0. 2866 nm = 2. 866 10 -8 cm Atomic mass = 55. 847 g/mol Volume of unit cell = cm 3/cell = (2. 866 10 -8 cm)3 = 23. 54 10 -24 Avogadro’s number NA = 6. 02 1023 atoms/mol The Science and Engineering of Materials, 4 th ed Donald R. Askeland – Pradeep P. Phulé 87

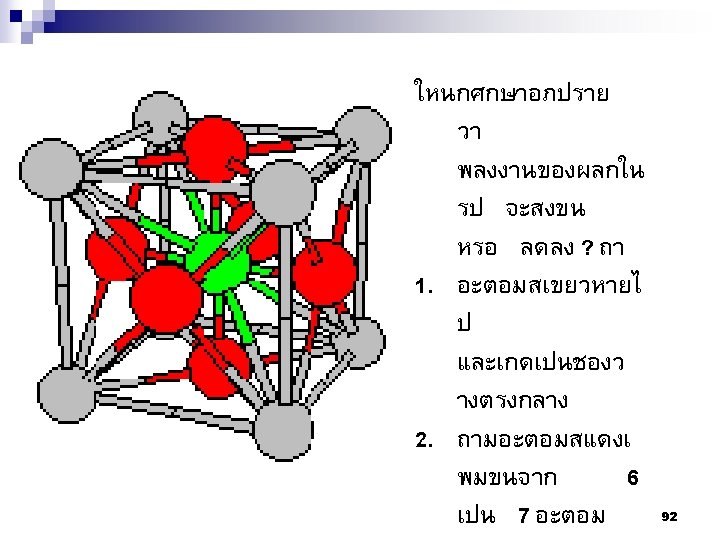
ทบทวน What is the structure of materials? n How is the crystal structure created ? n What are three major crystal structures? n 90

Type of Defects ทเกดขนจะถกแบงโดยขนาด ซงไดแก 1. Point defects (1 or 2 atomic positions) 2. Line defects ( 1 -dimensional defects) 3. Planar defects (2 -dimensional defects) 95

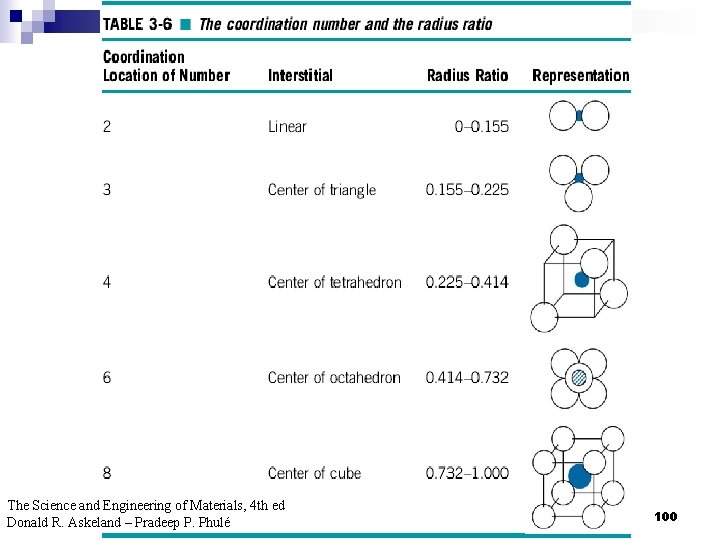
The Science and Engineering of Materials, 4 th ed Donald R. Askeland – Pradeep P. Phulé 100

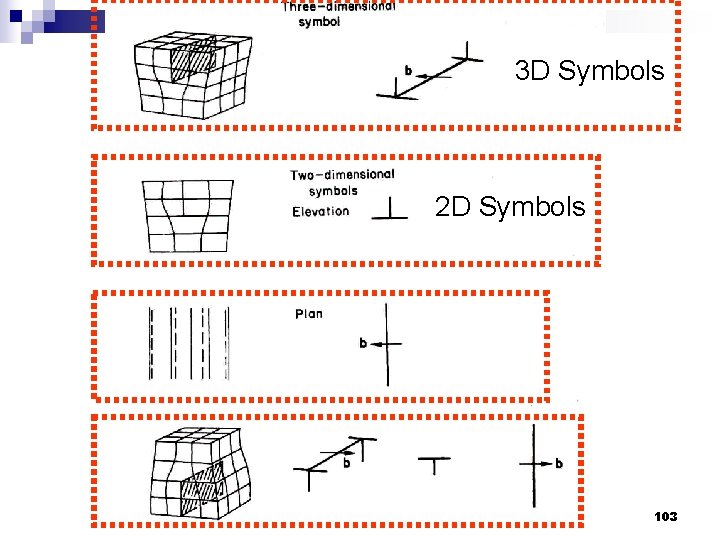
3 D Symbols 2 D Symbols 103

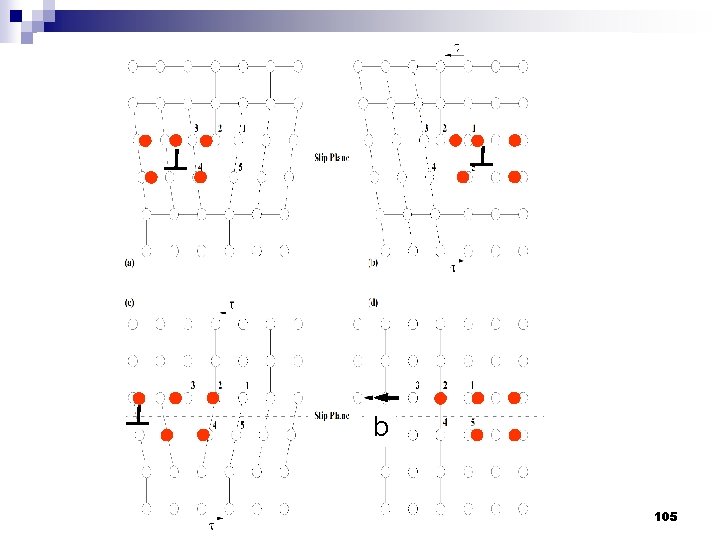
b 105

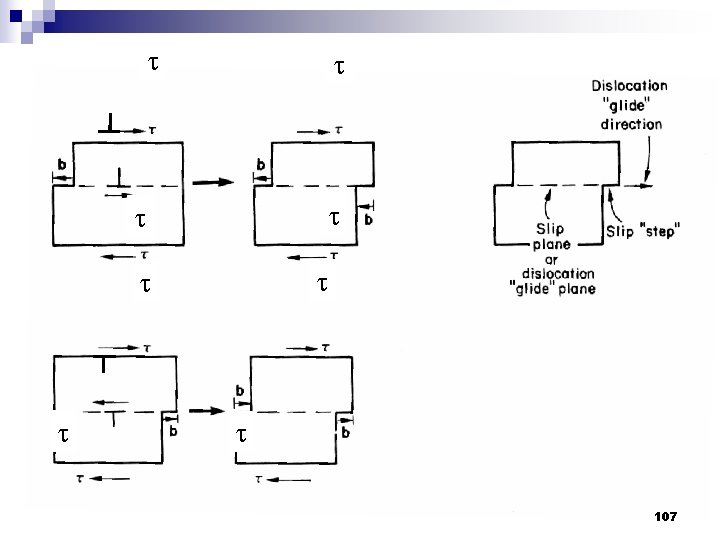
107

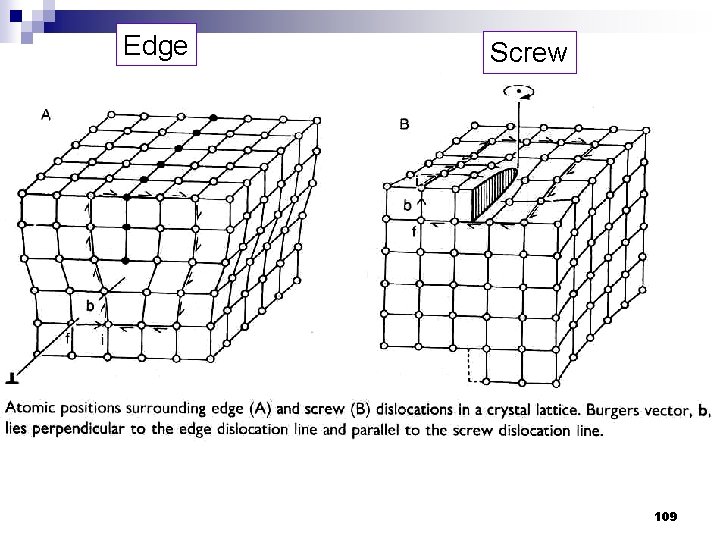
Edge Screw 109

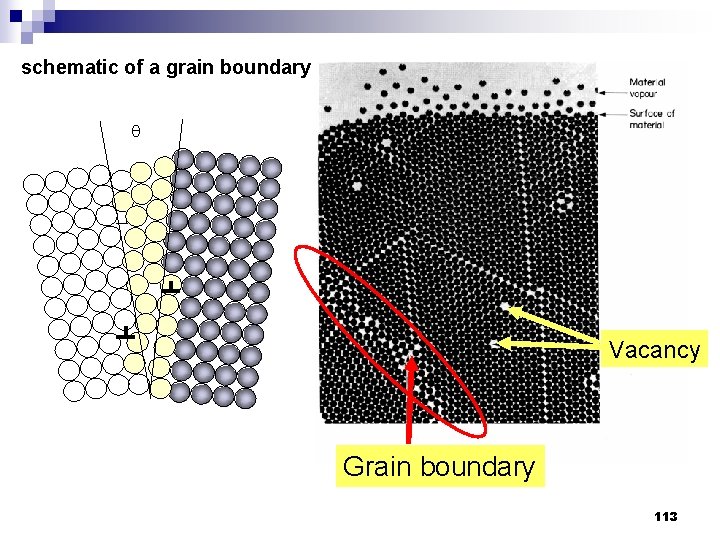
schematic of a grain boundary Vacancy Grain boundary 113