Crystal Structure Continued NOTE Again much discussion many

Crystal Structure Continued! NOTE!! Again, much discussion & many figures in what follows was constructed from lectures posted on the web by Prof. Beşire GÖNÜL (Turkey). She has done an excellent job covering many details of crystallography & she illustrates with many very nice pictures of lattice structures. Her lectures are posted Here: http: //www 1. gantep. edu. tr/~bgonul/dersnotlari/. Her homepage is Here: http: //www 1. gantep. edu. tr/~bgonul/

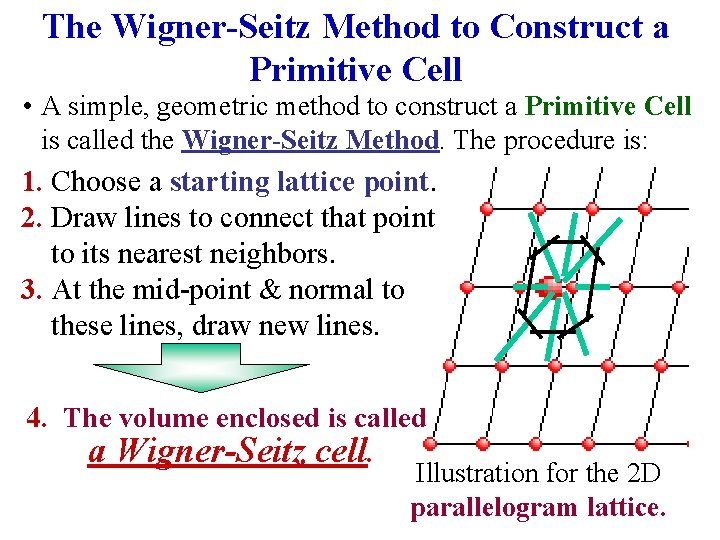
The Wigner-Seitz Method to Construct a Primitive Cell • A simple, geometric method to construct a Primitive Cell is called the Wigner-Seitz Method. The procedure is: 1. Choose a starting lattice point. 2. Draw lines to connect that point to its nearest neighbors. 3. At the mid-point & normal to these lines, draw new lines. 4. The volume enclosed is called a Wigner-Seitz cell. Illustration for the 2 D parallelogram lattice.

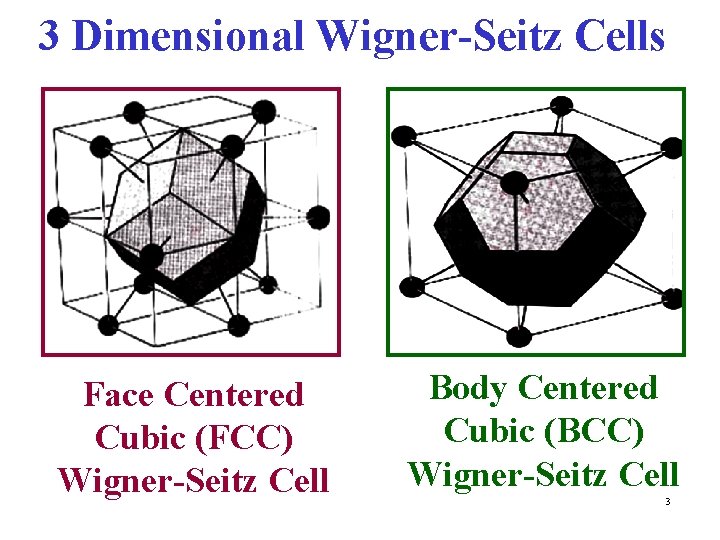
3 Dimensional Wigner-Seitz Cells Face Centered Cubic (FCC) Wigner-Seitz Cell Body Centered Cubic (BCC) Wigner-Seitz Cell 3

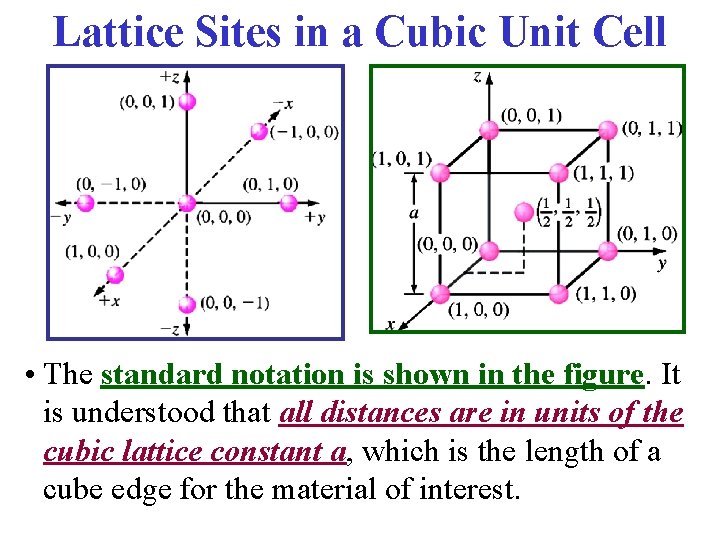
Lattice Sites in a Cubic Unit Cell • The standard notation is shown in the figure. It is understood that all distances are in units of the cubic lattice constant a, which is the length of a cube edge for the material of interest.

Directions in a Crystal: Standard Notation • See Figure. Choose an origin, O. This choice is arbitrary, because every lattice point has identical symmetry. Then, consider the lattice vector joining O to any point in space, say point T in the figure. [111] direction As we’ve seen, this vector can be written T = n 1 a 1 + n 2 a 2 + n 3 a 3

Directions in a Crystal: Standard Notation A lattice Vector T = n 1 a 1 + n 2 a 2 + n 3 a 3 • In order to distinguish a Lattice Direction from a Lattice Point, (n 1 n 2 n 3), the 3 integers are [111] direction enclosed in square brackets [. . . ] instead of parentheses (. . . ), which are reserved to indicate a Lattice Point. In direction [n 1 n 2 n 3], n 1 n 2 n 3 are the smallest integers possible for the relative ratios.

Examples 210 X = 1, Y = ½, Z = 0 [1 ½ 0] [2 1 0] X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2]

Negative Directions • When we write the direction [n 1 n 2 n 3] depending on the origin, negative directions are written as R = n 1 a 1 + n 2 a 2 + n 3 a 3 With a bar above the negative integers. To specify the direction, the smallest possible integers must be used. 8

Examples of Crystal Directions X = 1, Y = 0, Z = 0 [100] X = -1, Y = -1, Z = 0 [110]

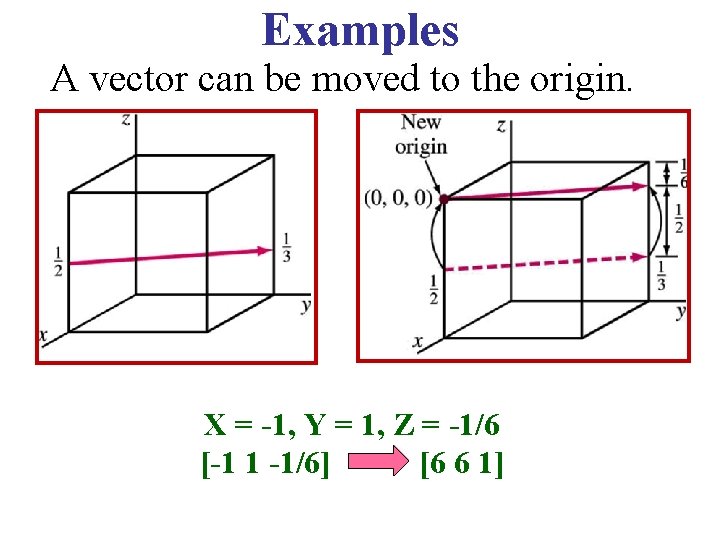
Examples A vector can be moved to the origin. X = -1, Y = 1, Z = -1/6 [-1 1 -1/6] [6 6 1]

Crystal Planes • Within a crystal lattice it is possible to identify sets of equally spaced parallel planes. These are called lattice planes. • In the figure, the density of lattice points on each plane of a set is the same & all lattice points are contained on each set of planes. The set of planes for a 2 D lattice. b b a a

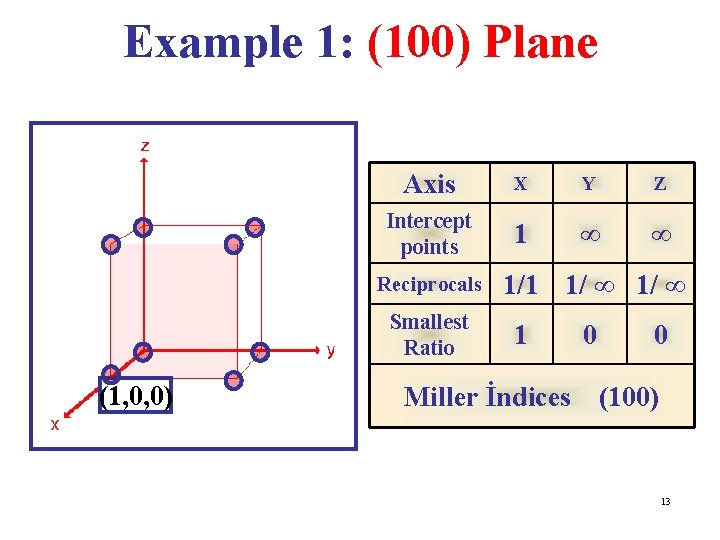
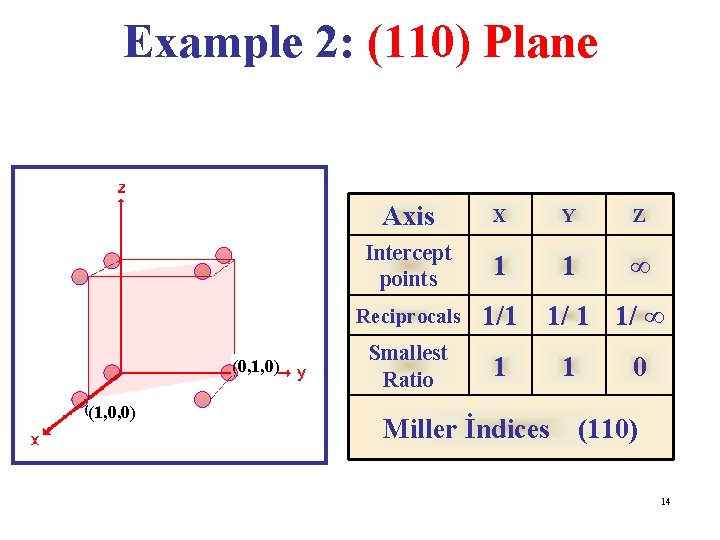
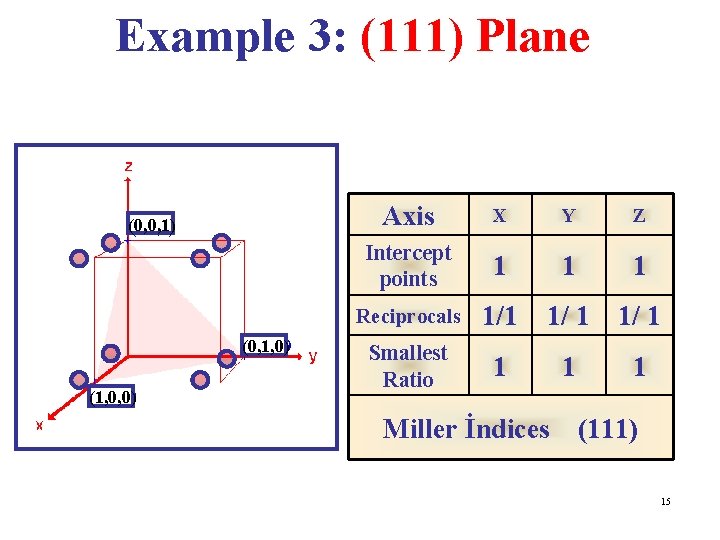
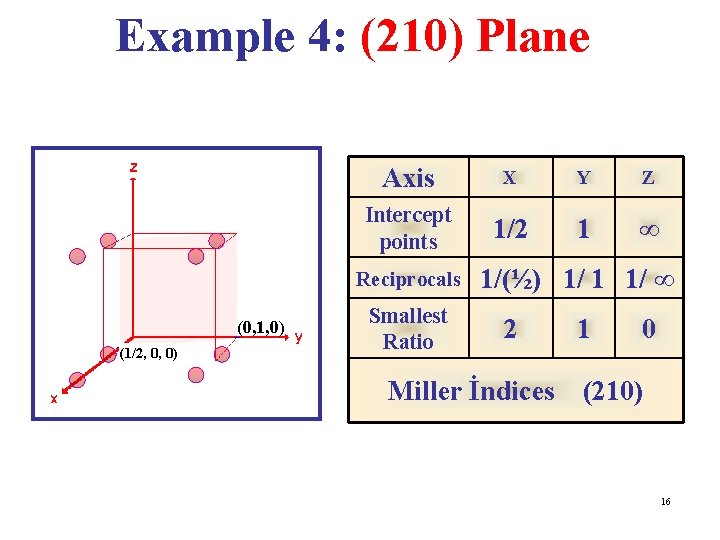
Miller Indices • Miller Indices are a symbolic vector representation for the orientation of an atomic plane in a crystal lattice & are defined as the reciprocals of the fractional intercepts which the plane makes with the crystallographic axes. • To find the Miller indices of a plane, take the following steps: 1. Determine the intercepts of the plane along each of the three crystallographic directions. 2. Take the reciprocals of the intercepts. 3. If fractions result, multiply each by the denominator of the smallest fraction. 12

Example 1: (100) Plane Axis X Y Z Intercept points 1 ∞ ∞ Reciprocals Smallest Ratio (1, 0, 0) 1/1 1/ ∞ 1 0 0 Miller İndices (100) 13

Example 2: (110) Plane (0, 1, 0) (1, 0, 0) Axis X Y Z Intercept points 1 1 ∞ Reciprocals 1/1 Smallest Ratio 1 1/ ∞ 1 0 Miller İndices (110) 14

Example 3: (111) Plane (0, 0, 1) (0, 1, 0) (1, 0, 0) Axis X Y Z Intercept points 1 1 1 Reciprocals 1/1 1/ 1 Smallest Ratio 1 1 1 Miller İndices (111) 15

Example 4: (210) Plane Axis X Y Z Intercept points 1/2 1 ∞ Reciprocals (0, 1, 0) (1/2, 0, 0) Smallest Ratio 1/(½) 1/ 1 1/ ∞ 2 1 0 Miller İndices (210) 16

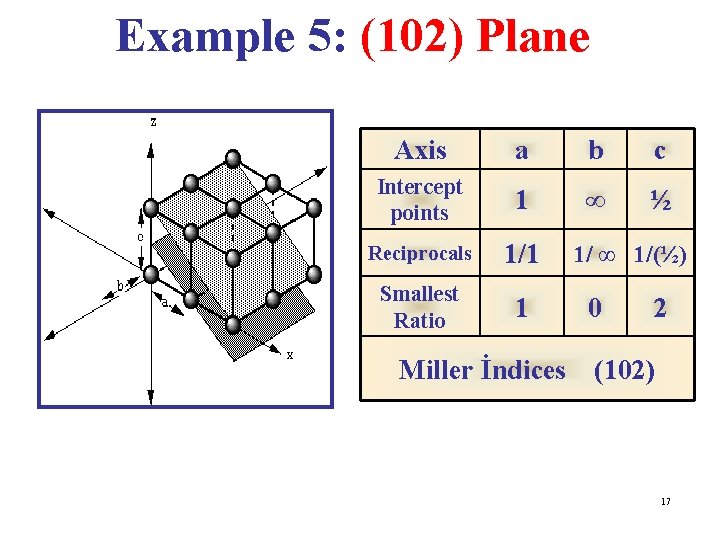
Example 5: (102) Plane Axis a b c Intercept points 1 ∞ ½ Reciprocals 1/1 Smallest Ratio 1 1/ ∞ 1/(½) 0 2 Miller İndices (102) 17

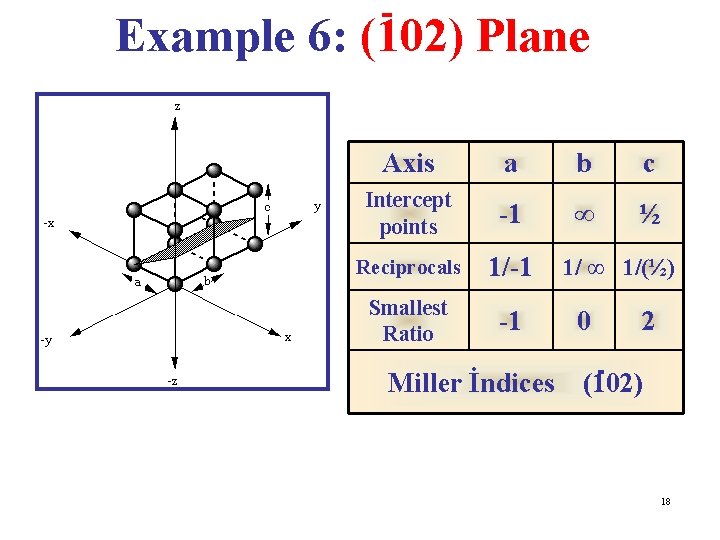
Example 6: (102) Plane Axis a b c Intercept points -1 ∞ ½ Reciprocals 1/-1 Smallest Ratio -1 Miller İndices 1/ ∞ 1/(½) 0 2 (102) 18

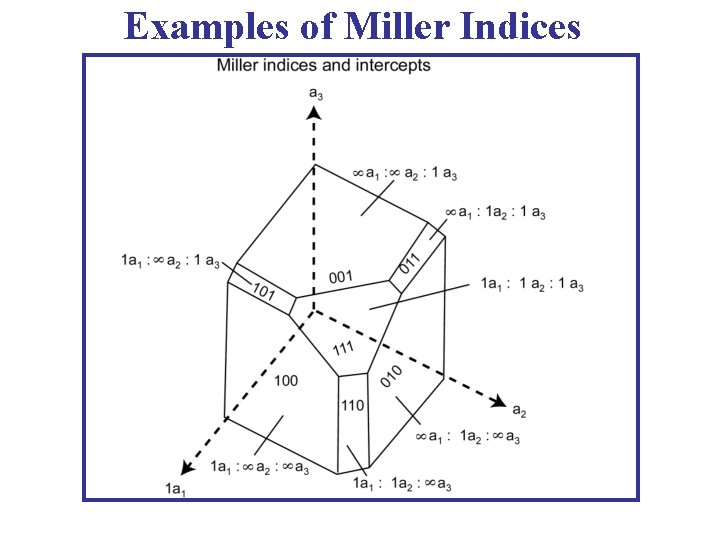
Examples of Miller Indices [2, 3, 3] • See the figure. • Consider the plane shaded in yellow: 2 2 3 Plane intercepts axes at Reciprocal numbers are: Miller Indices of the plane: (2, 3, 3) Indices of the direction: [2, 3, 3]

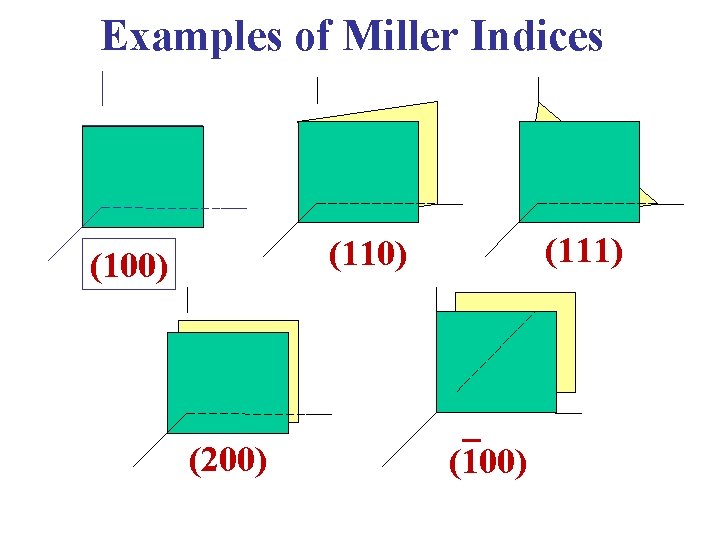
Examples of Miller Indices (111) (110) (100) (200) (100)

Examples of Miller Indices

Indices of a Family of Planes • Sometimes. when the unit cell has rotational symmetry, several nonparallel planes may be equivalent by virtue of this symmetry, in which case it is convenient to lump all these planes in the same Miller Indices, but with curly brackets. • So, indices {h, k, l} represent all of the planes equivalent to the plane (hkl) through rotational symmetry. 22