Convexity in Itemset Spaces Limsoon Wong Institute for

Convexity in Itemset Spaces Limsoon Wong Institute for Infocomm Research Copyright © 2005 by Limsoon Wong

Plan • Frequent itemsets – – Convexity Equivalence classes, generators, & closed patterns Plateau representation Efficient mining of generators & closed patterns • Emerging patterns • Odds ratio patterns • Relative risk patterns Copyright © 2005 by Limsoon Wong

Frequent Itemsets Copyright © 2005 by Limsoon Wong

Association Rules • Buyer’s behaviour in supermarket • Mgmt are interested in rules such as Copyright © 2005 by Limsoon Wong

Frequent Itemsets • List of items: I = {a, b, c, d, e, f} • List of transactions: T = {T 1, T 2, T 3, T 4, T 5} • • • T 1 = {a, c, d} T 2 = {b, c, e} T 3 = {a, b, c, e, f} T 4 = {b, e} T 5 = {a, b, c, e} • For each itemset I I, sup(I, T) = |{ Ti T | I Ti}| • Freq itemsets: FT = F(ms, T) ={I I | sup(I, T) ms} Copyright © 2005 by Limsoon Wong

A Priori Property • Freq itemset from our example: ms=2 • A priori property: I FT I’ I, I’ FT Copyright © 2005 by Limsoon Wong

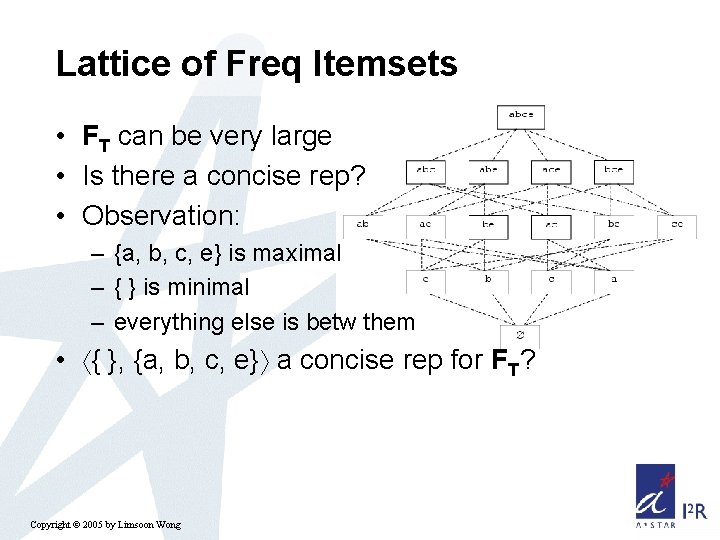
Lattice of Freq Itemsets • FT can be very large • Is there a concise rep? • Observation: – {a, b, c, e} is maximal – { } is minimal – everything else is betw them • { }, {a, b, c, e} a concise rep for FT? Copyright © 2005 by Limsoon Wong

Convexity • An itemset space S is convex if, for all X, Y S st X Y, we have Z S whenever X Z Y • An itemset X is most general in S if there is no proper subset of X in S. These itemsets form the left bound L of S • An itemset is most specific in S if there is no proper superset of X in S. These itemsets form the right bound R of S • L, R is a concise rep of S • [L, R] = { Z | X L, Y R, X Z Y} = S Copyright © 2005 by Limsoon Wong

Convexity of Freq Itemsets • Proposition 1: The freq itemset space is convex L, R is a concise rep for a freq itemset space Copyright © 2005 by Limsoon Wong

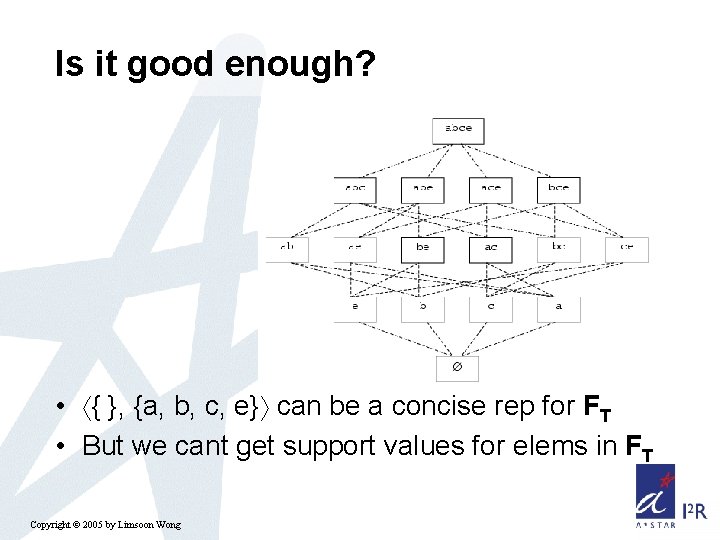
Is it good enough? • { }, {a, b, c, e} can be a concise rep for FT • But we cant get support values for elems in FT Copyright © 2005 by Limsoon Wong

What is a good concise rep? • A good concise rep for FT should enable these tasks below efficiently, w/o accessing T again: – – – Task 1: Enumerate {I FT} Task 2: Enumerate {(I, sup(I, T)) | I FT } Task 3: Given I, decide if I FT, & if so report sup(I, T) Task 4: Enumerate itemsets w/ sup in a given range etc. Copyright © 2005 by Limsoon Wong

Closed Itemset Rep • A pattern is a closed pattern if each of its supersets has a smaller support than it • The closed itemset rep of FT is CR ={ (I, sup(I, T)) | I FT, I is closed pattern} • Proposition 2: {(I, sup(I, T)) | I FT} = {(I, max{sup(I’, T) | (I’, sup(I’, T)) CR, I I’}) | I FT} May be inefficient for Tasks 2, 3, 4 Copyright © 2005 by Limsoon Wong

Generator Rep • A pattern is a generator if each of its subsets has a larger support than it • The generator rep of FT is GR = {(I, sup(I, T)) | I FT, I is generator}, GBd- where GBd- are the min in-freq itemsets • Proposition 3: {(I, sup(I, T)) | I FT} = {(I, min{sup(I’, T) | I’ GR, I’ I}) | I FT} May be inefficient for Tasks 2, 3, 4 Copyright © 2005 by Limsoon Wong

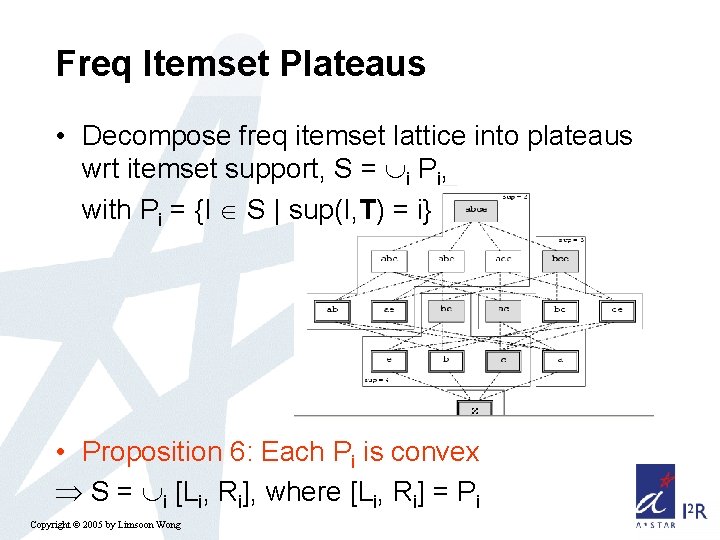
Freq Itemset Plateaus • Decompose freq itemset lattice into plateaus wrt itemset support, S = i Pi, with Pi = {I S | sup(I, T) = i} • Proposition 6: Each Pi is convex S = i [Li, Ri], where [Li, Ri] = Pi Copyright © 2005 by Limsoon Wong

From Generators & Closed Patterns To Equivalence Classes • The equivalence class of an itemset I is [I]T = { I’ | { Ti T | I’ Ti} = {Tj T | I Tj}} • Proposition 4: [I]T is convex. Furthermore, if [L, R] = [I]T, then L = min [I]T, and R = max [I]T is a singleton • Proposition 5: – An itemset I is a generator iff I min [I]T – An itemset I is a closed pattern iff I max [I]T Copyright © 2005 by Limsoon Wong

Plateaus = Generators + Closed Patterns • Theorem 7: Let [Li, Ri] = Pi be a freq itemset plateau of FT. Then – Pi = [X 1]T … … [Xk]T, where Ri = {X 1, …, Xk} – Ri are the closed patterns in Pi – Li = i min [Xi]T are the generators in Pi Copyright © 2005 by Limsoon Wong

Freq Itemset Plateau Rep • The freq itemset plateau rep of FT is PR = {( Li, Ri , i) | i ms} where [Li, Ri] is plateau at support level i in FT • Proposition 8: {(I, sup(I, T)) | I FT} = {(I, i)| ( Li, Ri , i) PR, X Li, Y Ri, X I Y} All 4 tasks are obviously efficient Copyright © 2005 by Limsoon Wong

Remarks • PR is a good concise rep for freq itemsets • PR is more flexible compared to other reps • PR unifies diff notions used in data mining • Nice. . . But can we mine PR fast? Copyright © 2005 by Limsoon Wong

Mining PR Fast • To mine PR fast, mine its borders fast • To mine its borders fast, mine equiv classes in the plateau fast • To mine equiv classes fast, mine generators & closed patterns of equivalence classes fast Copyright © 2005 by Limsoon Wong

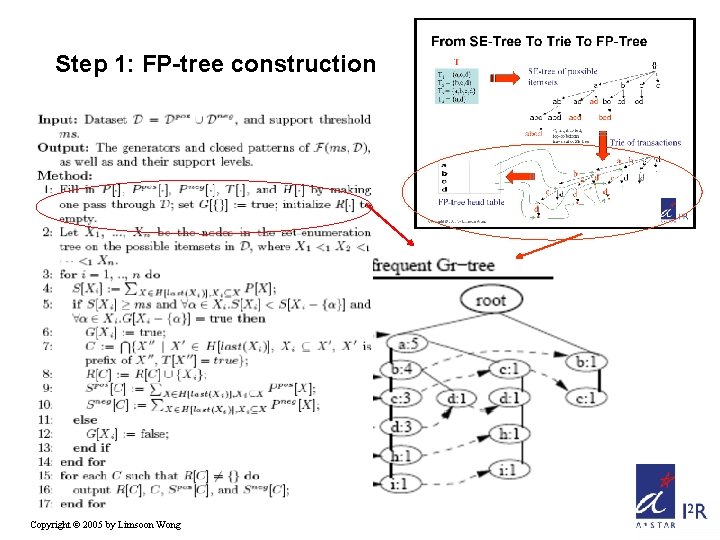
From SE-Tree To Trie To FP-Tree T T 1 = {a, c, d} T 2 = {b, c, d} T 3 = {a, b, c, d} T 4 = {a, d} SE-tree of possible itemsets a ab ac abd acd b Copyright © 2005 by Limsoon Wong . d • b c ad bc bd cd c . . . d d • c d bcd <1: right-to-left, top-to-bottom traversal of SE-tree abcd FP-tree head table {} Trie of transactions a b c. . d. c d. • d • . . d .

GC-growth: Fast Simultaneous Mining of Generators & Closed Patterns Copyright © 2005 by Limsoon Wong

Step 1: FP-tree construction Copyright © 2005 by Limsoon Wong

Step 2: Right-to-left, top-to-bottom traversal Copyright © 2005 by Limsoon Wong

Step 5: Confirm Xi is generator Proposition 9: Generators enjoy the apriori property. That is every subset of a generator is also a generator Copyright © 2005 by Limsoon Wong

Step 7: Find closed pattern of Xi Proposition 10: Let X be a generator. Then the closed pattern of X is {X’’| X’ H[last(X)], X X’, X’ prefix of X’’, T[X’’] = true}. Copyright © 2005 by Limsoon Wong

Correctness of GC-growth • Theorem 11: GC-growth is sound and complete for mining generators and closed patterns Copyright © 2005 by Limsoon Wong

Performance of GC-growth • GC-growth is mining both generators and closed patterns • But is comparable in speed to the fastest algorithms that mined only closed patterns Copyright © 2005 by Limsoon Wong

Emerging Patterns Copyright © 2005 by Limsoon Wong

Differentiation and Contrast edible mushrooms poisonous mushrooms x% 0% EPs Example: {odor=none, gill_size=broad, ring_number=1} 64% (edible) vs 0% (poisonous) Copyright © 2005 by Limsoon Wong

Emerging Patterns • An emerging pattern is a set of conditions – usually involving several features – that most members of a class P satisfy – but none or few of the other class N satisfy I is emerging pattern if sup(I, P) / sup(I, N) > k, for some fixed threshold k NB: For this talk, we restrict ourselves to “jumping” emerging patterns Copyright © 2005 by Limsoon Wong

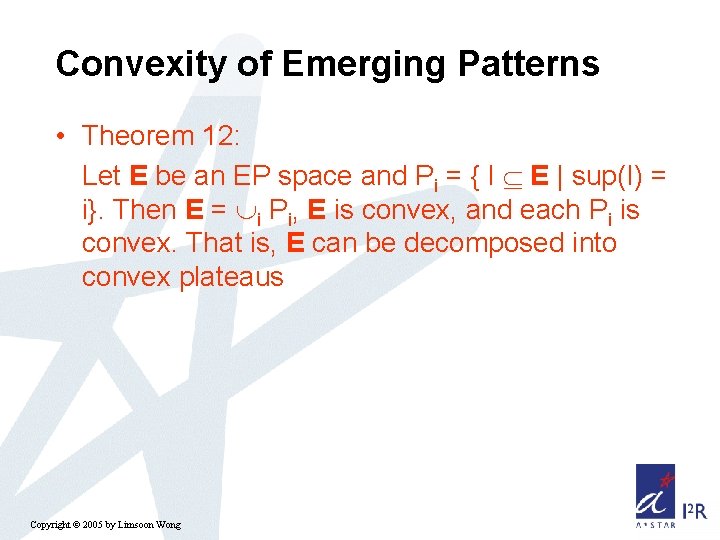
Convexity of Emerging Patterns • Theorem 12: Let E be an EP space and Pi = { I E | sup(I) = i}. Then E = i Pi, E is convex, and each Pi is convex. That is, E can be decomposed into convex plateaus Copyright © 2005 by Limsoon Wong

EP Plateau Rep • A concise rep for E = i Pi is EP plateau rep: EP_PR = { ( Li, Ri , i) | [Li, Ri] = Pi} • Proposition 13: {(I, sup(I)) | I E} = { (I, i) | ( Li, Ri , i) EP_PR, X Li, Y Ri, X I Y} All 4 tasks are obvious efficient Copyright © 2005 by Limsoon Wong

Efficient Mining of EP_PR • Modify GC-growth so that for each equiv class C, it outputs its support in +ve transactions Spos[C] & in -ve transactions Sneg[C] • Then [R[C], C] are emerging patterns if Spos[C] / Sneg[C] > k NB. Assume threshold for EP is k Copyright © 2005 by Limsoon Wong

Odds Ratio Patterns Copyright © 2005 by Limsoon Wong

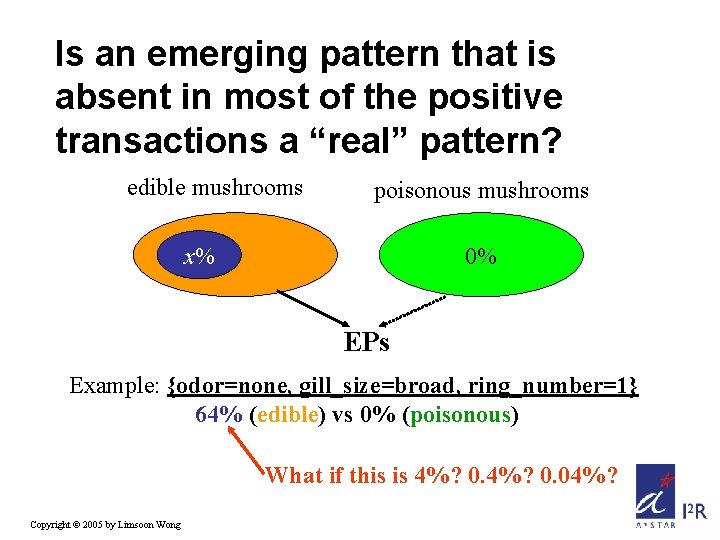
Is an emerging pattern that is absent in most of the positive transactions a “real” pattern? edible mushrooms poisonous mushrooms x% 0% EPs Example: {odor=none, gill_size=broad, ring_number=1} 64% (edible) vs 0% (poisonous) What if this is 4%? 0. 04%? Copyright © 2005 by Limsoon Wong

Odds Ratio • Odds ratio for a (compound) factor P in a casecontrol study D is OR(P, D) = (PD, ed / PD, -d) / (PD, e- / PD, --) P is a odds ratio pattern if OR(P, D) > k, for some threshold k Copyright © 2005 by Limsoon Wong

Nonconvexity of Odds Ratio Pattern Space • Proposition 14: Let Sk. OR(ms, D) = { P F(ms, D) | OR(P, D) k}. Then Sk. OR(ms, D) is not convex Copyright © 2005 by Limsoon Wong

Convexity of Odds Ratio Pattern Space Plateaus The space of odds ratio • Theorem 15: patterns is not convex in OR Let Sn, k (ms, D) = { P general, but becomes F(ms, D) | PD, ed=n, convex when stratified OR(P, D) k}. Then into plateaus based on support levels Sn, k. OR(ms, D) is The space of odds ratio convex patterns can be concisely represented by plateau borders Copyright © 2005 by Limsoon Wong

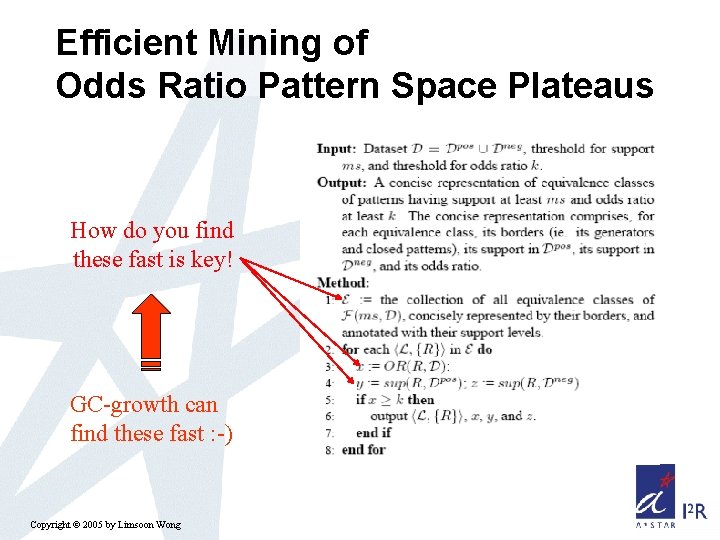
Efficient Mining of Odds Ratio Pattern Space Plateaus How do you find these fast is key! GC-growth can find these fast : -) Copyright © 2005 by Limsoon Wong

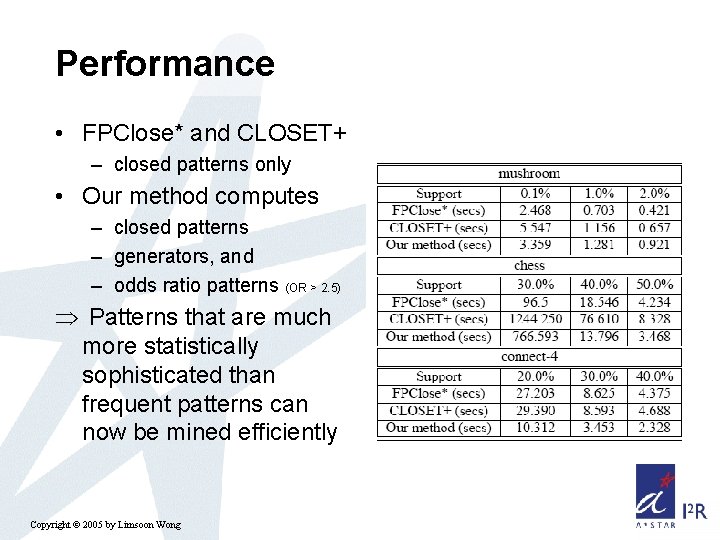
Performance • FPClose* and CLOSET+ – closed patterns only • Our method computes – closed patterns – generators, and – odds ratio patterns (OR > 2. 5) Patterns that are much more statistically sophisticated than frequent patterns can now be mined efficiently Copyright © 2005 by Limsoon Wong

Relative Risk Patterns Copyright © 2005 by Limsoon Wong

Relative Risk • Relative risk for a (compound) factor P in a prospective study D is P is a relative risk pattern if RR(P, D) > k, for some threshold k Copyright © 2005 by Limsoon Wong

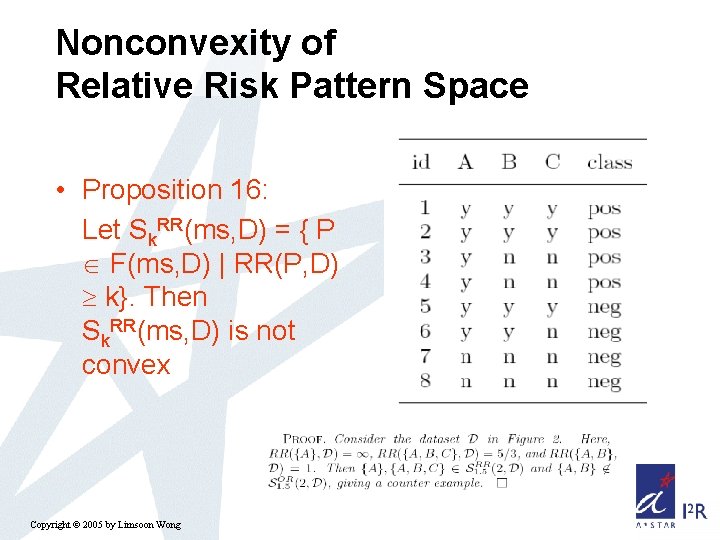
Nonconvexity of Relative Risk Pattern Space • Proposition 16: Let Sk. RR(ms, D) = { P F(ms, D) | RR(P, D) k}. Then Sk. RR(ms, D) is not convex Copyright © 2005 by Limsoon Wong

Convexity of Relative Risk Pattern Space Plateaus The space of relative • Theorem 17: risk patterns is not RR Let Sn, k (ms, D) = { P convex in general, but F(ms, D) | PD, ed=n, becomes convex when RR(P, D) k}. Then stratified into plateaus based on support levels Sn, k. RR(ms, D) is The space of relative convex risk patterns can be concisely represented by plateau borders Copyright © 2005 by Limsoon Wong

Efficient Mining of Relative Risk Pattern Space Plateaus How do you find these fast is key! x : = RR(R, D); GC-growth can find these fast : -) Copyright © 2005 by Limsoon Wong

Concluding Remarks • Equiv classes & plateaus are fundamental in – – Frequent itemsets Emerging patterns Odds ratio patterns Relative risk patterns, . . . • Equiv classes & plateaus of these complex patterns are convex spaces Complex pattern spaces are concisely representable by borders Complex pattern spaces can be efficiently and completely mined Copyright © 2005 by Limsoon Wong

Future Works Copyright © 2005 by Limsoon Wong

Improve Implementations • Modular pattern mining by construction of a fast equiv class generator and multiple statistical condition filters Generate borders of equiv classes & support levels Test for odds ratio Test for relative risk Copyright © 2005 by Limsoon Wong Test for 2 • Impact of item ordering • Impact of pushing complex statistical filters deeper into equivalence class generators

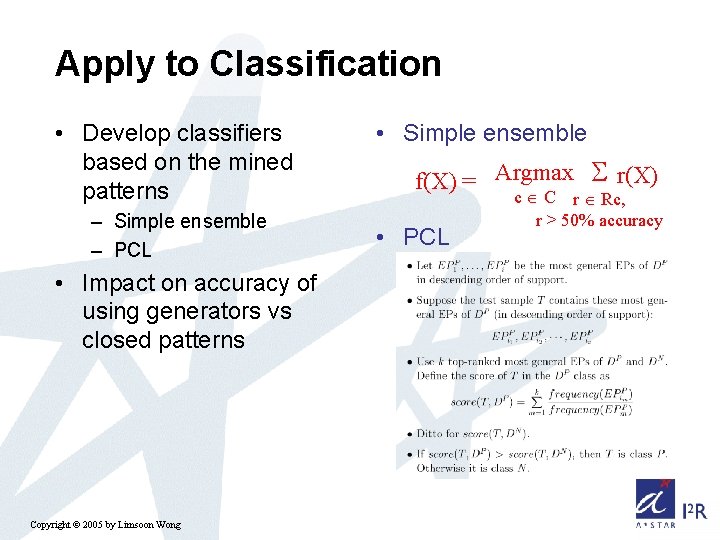
Apply to Classification • Develop classifiers based on the mined patterns – Simple ensemble – PCL • Impact on accuracy of using generators vs closed patterns Copyright © 2005 by Limsoon Wong • Simple ensemble f(X) = Argmax r(X) • PCL c C r Rc, r > 50% accuracy

Enrich Data Mining Foundations • Increase statistical sophistication of patterns mined • Increase dimensions and size of data handled Copyright © 2005 by Limsoon Wong

Acknowledgements • • Haiquan Li Jinyan Li Mengling Feng Yap Peng Tan Copyright © 2005 by Limsoon Wong