Tuple Spaces and Java Spaces CS 614 Bill

Tuple Spaces and Java. Spaces CS 614 Bill Mc. Closkey

Tuple Spaces n n A flexible technique for parallel and distributed computing Similar to message passing Data exists in a “tuple space” All processors can access the space
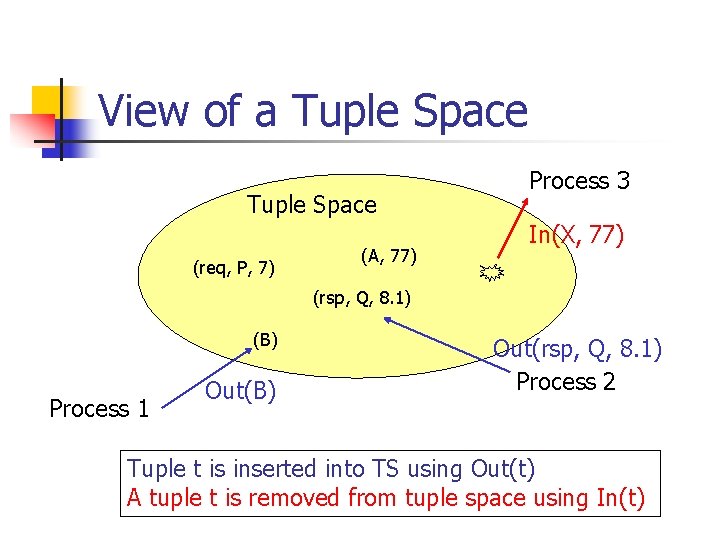
View of a Tuple Space (req, P, 7) (A, 77) Process 3 In(X, 77) (rsp, Q, 8. 1) (B) Process 1 Out(B) Out(rsp, Q, 8. 1) Process 2 Tuple t is inserted into TS using Out(t) A tuple t is removed from tuple space using In(t)

Tuple Types: Simple Case n n n A tuple is inserted into TS using Out(P, x, y, z) (assume x, y, z integers) The tuple is removed from TS using In(P, a: integer, b: integer, c: integer) The result: a=x, b=y, c=z P is the name of the tuple Also have Read, similar to In, but tuple is not removed from TS

Formal vs. Actual Parameters n Parameters of the form “p: t” are formal parameters n n Other parameters are actual parameters In and Out accept both formal and actual parameters Op(Req, 77. 2, i: integer, true, s: string)

Structured Naming n n n An actual parameter to In forms part of the name of the tuple to be found Formal parameters are filled with the other values from the tuple Example: In(P, 2, j: boolean, 77. 1) requests a tuple with structured name “P, 2, , 77. 1”

Structured Naming n n Out may also have formal parameters Example: n n n The call Out(A, 4, j: integer) is made A call of In(A, i: integer, 77) finds this tuple and sets i=4 A call of In(A, i: integer, 88) also finds it Formal parameters to Out may never be matched with formal parameters to In! The scope of the parameter is restricted to the Out call itself

Concurrency n n If multiple tuples are available to an In call, one is selected nondeterministically If nothing is available, In blocks Tuples operations are atomic A simple shared variable update: n n In(Var, value: integer) Out(Var, new_value)

Properties n A little like message passing, but n n n A little like shared memory, but n n Messages can stay alive after receipt Messages aren’t directed to a certain party Structured Operations are atomic Space uncoupling Time uncoupling

Active Monitors n n n Similar to a monitor, but operations are run in a separate process Waits for tuples to appear with commands for the monitor to run Each command is run atomically Basically, just doing message passing Messages are buffered up in TS during processing

Locking n n Useful primitives are easy to write A mutex: Lock: In(L) Unlock: Out(L) n A semaphore: Initialize the semaphore to n by writing n tuples Decrement by taking one of the tuple

Distributed Naming n n n Tuples not addressed to a certain node Could have a cluster of processes accepting requests A tuple (Request, …) is served by the first available process in the cluster No need for a dispatcher Tuple names can be used for distributed addressing
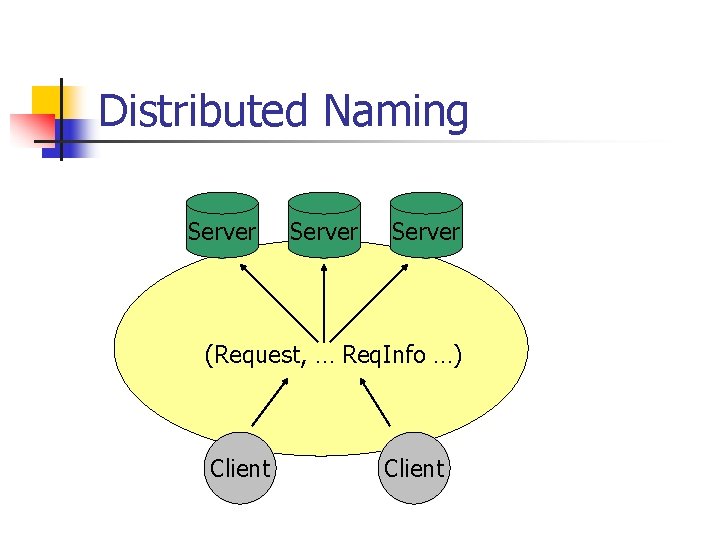
Distributed Naming Server (Request, … Req. Info …) Client

Continuation Passing n n A programming model Data flows through tuple space from one process to another Process writes a tuple, then blocks on a “reply” tuple Reply tuple determines the next action
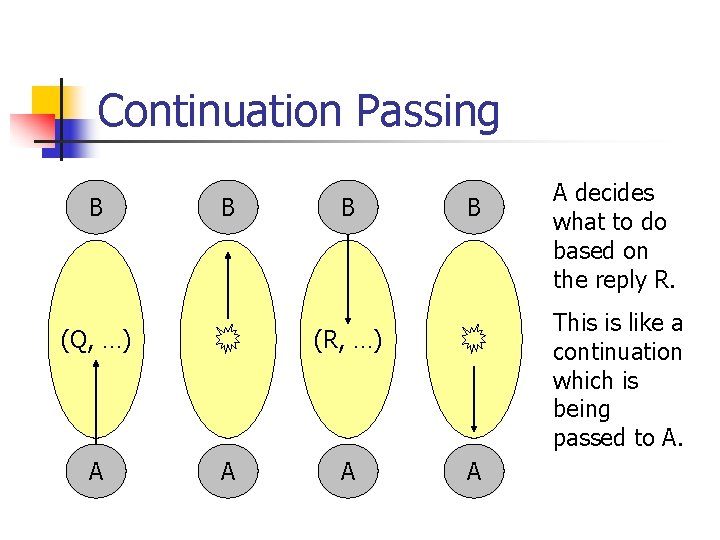
Continuation Passing B B (Q, …) A B B This is like a continuation which is being passed to A. (R, …) A A A decides what to do based on the reply R. A

Implementation n n Linda implementations can be slow A tuple is usually stored on one processor, its “home” Other processors broadcast queries for locations of tuples Also could use a hash function Having a single home guarantees atomicity

Linda n n n A concurrent programming language Uses tuple spaces Tuple spaces are more than an API They’re linked to a programming style Linda makes it efficient to program using this style

Ordering n n In and Read are nondeterministic In some sense, a total ordering is not guaranteed Example: Clients write command tuples into TS. Replicated servers execute the commands. Each server may read the commands in a different order. Result: Cannot use TSs for agreement

Problems n n n Linda is not fault-tolerant Processors are assumed not to fail If processor fails, its tuples can be lost At worst, entire system can fail If tuples are replicated, you run into standard agreement problems Linda offers no security

Java. Spaces n n A technology from Sun to add distributed computing to Jini “Ever since I first saw David Gelernter's Linda programming language almost twenty years ago, I felt that the basic ideas of Linda could be used to make an important advance in the ease of distributed and parallel programming. ” — Bill Joy

Java. Spaces Overview n n Java objects are stored in a Java. Space Operations: n n Write: Works like Out Read: Works like Read Take: Works like In Notify: Notifies an object when a matching entry is added to the space

Typing n n n Objects in the space have Java types Write copies an object into the space Read/Take/Notify(obj) look for a obj’ in the space satisfying: n n n type(obj’) type(obj) (subtype relation) obj. field null obj. field = obj’. field Fields that are only part of obj’ (due to subtyping) are not constrained

Timeouts and Liveness n n n Timeout improves liveness Operations like In and Read can timeout Objects added to the space are removed after their “lease” expires Timeout can prevent deadlock Leasing functions like garbage collection here

Transactions n n Operations can be bundled into atomic transactions Ongoing transactions don’t affect each other Observers see transactions as occurring sequentially But different observers may see different orders of transactions

Reliability n n Java. Spaces can be implemented in different ways Specification doesn’t require reliability Transactions preserve consistency when processes fail If the entire space fails, recovery is up to the implementation

Conclusions n n n Tuple spaces provide a very simple model for distributed computing Fault-tolerance is hard to get right Distributed naming impairs security n n Multiple Java. Spaces? Inefficient
- Slides: 26