Duration and convexity for FixedIncome Securities RES 9850

Duration and convexity for Fixed-Income Securities RES 9850 Real Estate Capital Market Professor Rui Yao Professor Yao

Duration and convexity: Outline z I. Macaulay duration z II. Modified duration z III. Examples z IV. The uses and limits of duration z V. Duration intuition z VI. Convexity 11/28/2020 Professor Yao 2

A Quick Note z Fixed income securities’ prices are sensitive to changes in interest rates z This sensitivity tends to be greater for longer term bonds z But duration is a better measure of term than maturity y Duration for 30 -year zero = 30 y Duration for 30 -year coupon with coupon payment < 30 y A 30 -year mortgage has duration less than a 30 -year bond with similar yield x. Amortization x. Prepayment option 11/28/2020 Professor Yao 3

I. (Macauly) duration z Weighted average term to maturity y Measure of average maturity of the bond’s promised cash flows z Duration formula: where: is the share of time t CF in the bond price and t is measured in years 11/28/2020 Professor Yao 4

Duration - The expanded equation z For an annual coupon bond z Duration is shorter than maturity for all bonds except zero coupon bonds z Duration of a zero-coupon bond is equal to its maturity 11/28/2020 Professor Yao 5

IV An Example – page 1 z Consider a 3 -year 10% coupon bond selling at $107. 87 to yield 7%. Coupon payments are made annually. 11/28/2020 Professor Yao 6

II. Modified duration (D*m) y Direct measure of price sensitivity to interest rate changes y Can be used to estimate percentage price volatility of a bond 11/28/2020 Professor Yao 7

Derivation of modified duration z So D*m measures the sensitivity of the % change in bond price to changes in yield 11/28/2020 Professor Yao 8

An Example – page 2 z Modified duration of this bond: z If yields increase to 7. 10%, how does the bond price change? z The percentage price change of this bond is given by: = – 2. 5661 . 1% = –. 2566% 11/28/2020 Professor Yao 9

An Example – page 3 z What is the predicted change in dollar terms? New predicted price: $107. 87 –. 2768 = $107. 5932 Actual dollar price (using PV equation): $107. 5966 11/28/2020 Professor Yao Good approximation! 10

Summary: Steps for finding the predicted price change z Step 1: Find Macaulay duration of bond. z Step 2: Find modified duration of bond. z Step 3: Recall that when interest rates change, the change in a bond’s price can be related to the change in yield according to the rule: y Find percentage price change of bond y Find predicted dollar price change in bond y Add predicted dollar price change to original price of bond Predicted new price of bond 11/28/2020 Professor Yao 11

V. Check your intuition z How does each of these changes affect duration? 1. Decreasing the coupon rate. verify this with a 10 -year bond with coupon rate from 5% to 15%, and ytm of 10% 2. Decreasing the yield-to-maturity. verify this property with a 10 -year bond with coupon rate of 10%, and ytm from 5% to 15% 3. Increasing the time to maturity. verify this property with a par bond with a coupon rate of 10%, and term from 5 to 15 years 11/28/2020 Professor Yao 12

V. Dollar Duration z We have derived the following relationship between duration and price changes (bond returns): z Hence z Note the term on the RHS of the equation above measures the (absolute value of) slope of the yield-price curve, which is also called dollar duration z We can then predict price changes using dollar duration: 11/28/2020 Professor Yao 13

Duration with intra-year compounding z In practice, lots of bonds do not pay annual coupon and we need to change the formula a bit to account for it z Some calculus (note: each step in summation is 1/m year so there are m*T terms in total) z So dollar duration z Duration 11/28/2020 Professor Yao 14

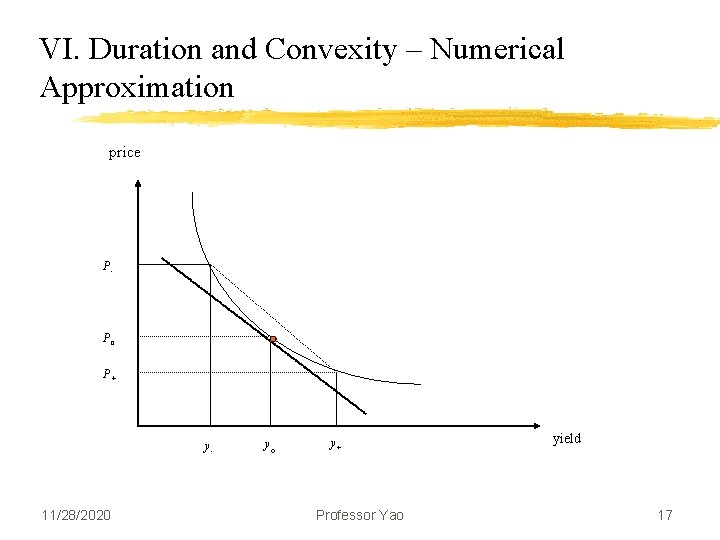
V. Effective Duration– Numerical Approximation z Instead of calculating modified duration based on weighing the time of cash flow with the present value share of the CF, and then modify by dividing by (1+y), we can numerically approximate the modified duration from the slope of price-yield chart: z The slope of the yield-price curve is the dollar duration 11/28/2020 Professor Yao 15

V. Effective Duration – Numerical Approximation z We can approximate the slope of the graph / dollar duration by averaging the forward and backward slope (“central difference method”) z The duration is then z The modified duration then can be estimated as z This approach directly uses the idea that the duration measures price sensitivity to interest rate y Can duration be negative? 11/28/2020 Professor Yao 16

VI. Duration and Convexity – Numerical Approximation price P- Po P+ y- 11/28/2020 y ° y+ Professor Yao yield 17

VI. Convexity z Duration is the first order approximation for percentage change in bond prices for a one percent change in yield to maturity y For a fixed rate non-callable bond, duration underestimates change when yield falls and overestimates when yield rises y The difference is captured by convexity y Convexity is typically positive for bond x Is this good or bad? z Mortgage is a difficult product to evaluate due to embedded call options y Duration tends to become shorter when interest becomes lower as borrower prepays mortgage y Duration becomes longer when interest rate becomes higher as borrower holds on to his mortgage y Negative convexity x Opposite to the case of a typical bond 11/28/2020 Professor Yao 18

V. Convexity z The forecast of price response using dollar duration is z Essentially it is a linear projection using the slope measured at yo y However as soon as you move away from yo the slope will change z The rate of slope change is captured by dollar convexity z A little calculus yields (take first order derivative of dollar duration with respect to yield) 11/28/2020 Professor Yao 19

V. Convexity – Numerical Approximation z What is the predicted dollar duration at y+ using dollar duration from yo and convexity measure at yo? z So the average of slopes at y+ and yo , which gives a better approximation of changes in prices when yield changes, is 11/28/2020 Professor Yao 20

V. Convexity z The forecast of price response using duration and convexity z In percentage term z The term is referred to as convexity 11/28/2020 Professor Yao 21

V. Convexity with intra-year coupons z Dollar convexity with intra-year coupons z Convexity with intra-year coupons 11/28/2020 Professor Yao 22

V. Effective Dollar Convexity – Numerical Approximation z Instead of analytical formula, in practice $ convexity is frequently approximated using numerical methods based on price-yield relations z Numerical approximation is very useful when cash flow size and timing are uncertain due to built-in options in the bond payments 11/28/2020 Professor Yao 23

V. Homework z z 30 year T-bond has a yield to maturity of 3. 0% and price at par, and coupon is paid annually. 1. Find out analytically the following measure at 3. 0%: x A. duration x B. modified duration x C. dollar duration x D. dollar convexity x E. convexity 2. Also calculate B, C, D, and E using numerical approximations using a step (delta y) of 1 basis point. How accurate is the approximation compared with analytical solutions from part 1? 3. Use dollar duration measure to predict price when yields change from 1% to 5% at 0. 5% interval. 4. Use both duration and convexity to predict bond price when yields change from 1% to 5% at 0. 5% interval. note: you can use either the analytical duration/convexity or their numerical approximation for question 3 and 4. 5. What do you conclude when comparing results from 3 and 4? Which one is more accurate and why? 11/28/2020 Professor Yao 24